题解：P1310 [NOIP2011 普及组] 表达式的值

前置芝士

在题目中，*号其实为&，⊕号其实为|。

对于这种表达式的题目，我们一般都要建一棵表达式树。这道题我也用到了树形 DP。其实大家应该都接触到过，在题目中叫你求这颗二叉树的大小，在某种意义上也是树形 DP。怎么整呢？我们在每个子树的空格处填入 \(0\) 和 \(1\)，得到结果 \(0\) 和 \(1\) 的方案数分别是多少。以下图片中的 \(L_0,L_1,R_0,R_1\) 分别表示左右子树算出来为 \(0\) 和 \(1\) 的方案数。

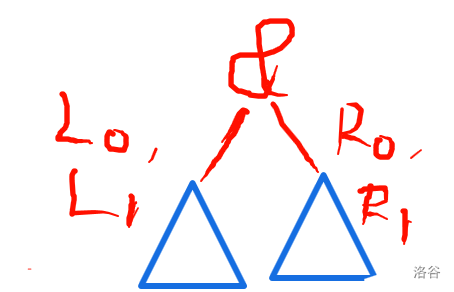
这个算出来为 \(0\) 的方案数为 \(L_0\cdot R_0+L_0\cdot R_1+L_1\cdot R_0\)。

这个算出来为 \(0\) 的方案数为 \(L_0\cdot R_0\)。

AC code：

#include <bits/stdc++.h>
using namespace std;
const int mod = 10007;
const int N = 101000;
struct info {
	int s0, s1;
};
int n, l1[N], l2[N], c1[N], c2[N];
char s[N];
info f(int l, int r) {
	info ans;
	if (l > r) {
		ans.s0 = 1;
		ans.s1 = 1;
		return ans;
	}
	if (l1[r] >= l) {
		info ansl = f(l, l1[r] - 1);
		info ansr = f(l1[r] + 1, r);
		ans.s0 = ansl.s0 * ansr.s0 % mod;
		ans.s1 = (ansl.s0 * ansr.s1 + ansl.s1 * ansr.s0 + ansl.s1 * ansr.s1) % mod;
		return ans;
	}
	if (l2[r] >= l) {
		info ansl = f(l, l2[r] - 1);
		info ansr = f(l2[r] + 1, r);
		ans.s1 = ansl.s1 * ansr.s1 % mod;
		ans.s0 = (ansl.s0 * ansr.s1 + ansl.s1 * ansr.s0 + ansl.s0 * ansr.s0) % mod;
		return ans;
	}
	if (s[l] == '(' && s[r] == ')')return f(l + 1, r - 1);
//	assert(false);
	return ans;
}
int main() {
	scanf("%d", &n);
	if (n == 0) {
		printf("1\n");
		return 0;
	}
	scanf("%s", s + 1);
	int x = 0;
	for (int i = 1; i <= n; i++) {
		if (s[i] == '(')x += 1;
		else if (s[i] == ')')x -= 1;
		else if (s[i] == '+')c1[x] = i;
		else if (s[i] == '*')c2[x] = i;
		l1[i] = c1[x];
		l2[i] = c2[x];
	}
	info ans = f(1, n);
	printf("%d", ans.s0);
}