树状数组

一 、什么是树状数组？

我们先来看一道题：

例题1：

　　已知N个正整数，接下来我们对这N个数进行M次操作，操作分为两类：

　　①将第X个数加上V；②询问区间(P1，P2]的和。

因为每次修改单点，查询区间，所以这类题是单点修改区间查询类；

如果不知道树状数组的话，我们可以选择暴力枚举：//暴力出奇迹

　　每次进行①时，就将第X个数加上V；

　　每次进行②时，就 for 一次求出(P1,P2]的总和和sum。

它的时间复杂度为O（N^2）。

为什么这么复杂？因为每改一个数，就会影响所有包括它的区间。

这时候，我们奇妙的树状数组就闪亮登场！！！

//此处应有掌声

树状数组是有人在求解另一问题时偶然发现的，

它完美的优化了求前缀和的问题（前缀和就是求a[i]与其前面所有数的和，即a[i]+a[i-1]+...+a[1]）

而(p1,p2]的和就等于p2的前缀和减去p1的前缀和

而树状数组求前缀和的速度非常快，是O(log(n))

数状数组长这样：

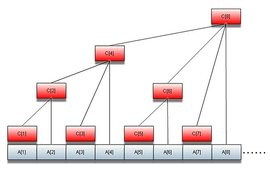
怎么实现呢?

我们定义一个数组c

c[i]=a[i]+a[i-1]+…+a[i–2^(k+1)+1](其中k是i在2进制下尾部0的个数)

我们把每个X的k叫做lowbit

我们先预处理求出每个c[i]，每次加上V后，

把包括X，即预处理中求和涵盖X的c数组元素都加V。

而且c数组的长度为log2(N)，所以时间复杂度只有O(log(N))

这就是树状数组。

但是怎么加，怎么查询呢，我们接下来会讲到。

1、找规律

我们针对两个例子，来看看如何维护c数组。

例子1：将a数组的第7个数+2

我们可以发现：我们需要将c[7],c[8],c[16]......加上2。

例子2：将a数组的第5个数+19

我们可以发现：我们需要将c[5],c[6],c[8],c[16]......加上19。

我们观察这两组数：7   8   16   |||   5   6   8   16

他们两两之差是：1   8   |||   1   2   8

恰好和上面k的性质相同：其差恰好为最大满足2^k是前面那个数的因数的自然数！

我们只需要将这个2^k求出来，运用函数的知识求出来就可以了！

定义函数lowbit

 #define lowbit(x) x&(-x)

为什么是x&(-x)？

由于计算机是用二进制工作的，我们举一个二进制的例子：

x=10001100

-x=01110011+1=01110100

x&(-x)=00000100

我么就可以求出2^k=(100)2=4

把(10001100)2 转化为10进制，是32+8+4=44

因此，我们可以用lowbit求出2^k。

 

2、第①个操作——加V

这一次我们献上代码：

void add(int x,int v){
　　while(x<=n)
　　{
　　    c[x]+=v;
　　    x+=lowbit(x);
　　}
}

这就是我们上面找的规律，是不是很简单？

 

3、查询query

这里的query其实指的是求前缀和，到时候我们需要用前缀和（q）-前缀和（p-1）

求前缀和的时候，这个关于k的规律展现出耀眼的光芒：

举一个栗子：

 

x=7时   我们要将c[7],c[6],c[4]加起来，7,6,4，的确满足那个规律！

因此我们还要用一次lowbit

int query(int p){
　　int sum=0;
　　while(x)
　　{ 
　　　　sum+=c[x];
　　　　x-=lowbit(x);
　　}
　　return sum;
}

---

 

三、主函数

int x,p,q,r,s;
cin>>n;
for(int i=1;i<=n;i++)
{
　　cin>>a[i];
　　c[i]+=a[i];
　　if(i+lowbit(i)<=n)
　　c[i+lowbit(i)]+=c[i];
}
cin>>m;
for(int i=1;i<=m;i++)
{
　　cin>>x;
　　if(x==1)
　　{
　　cin>>p>>q;
　　add(p,q);

　　}
　　if(x==2)
　　{
　　cin>>p>>q;
　　cout<<query(q)-query(p-1)<<endl;
　　}
}
return 0;

 

可能会有一点挤，链接：我们将会多次引用的Visualgo

---

 

四、回顾例题1

还记得例题一吗？那只是树状数组最简单的题目了，接下来我们分享一道不是裸题的树状数组和升级版的两道裸题。

1、小X手上有N个数字，他的爸爸让他抽纸牌，这些纸牌上正面有1个数字，可能是1，也可能是2。纸牌的背面有两个数字p,q。

如果纸牌正面上是1，则将小X手上的第p个数字换成q，如果纸牌正面是2，则计算出小X手上第p个数向后数q个这q+1个数的和。

输入格式：先输入一个正整数N（0<N<=10000），表示小X手上的数的数量，接着输入N个不超过10000的正整数，表示现在小X手上数字的值。

然后输入一个正整数M（0<M<=10000），表示抽纸牌的次数，然后输入纸牌的情况。

输入样例：5                                                                  输出样例：39

                 19  20 19 20 19

                 2

                 1 5 20

                 2 4 5

这道题很明显看出要用树状数组，如果用暴力，时间复杂度为O（MN），很大了吧，为了省时间，我们就需要使用使用树状数组。

不过要注意一下，与之前不同的是，操作1是将p改为q，相当于加上q-p，不是所有的题都是一样的！

---

 

五、升级版树状数组

1.（区间修改单点查询）：有N个整数，对他们进行M次操作，可能是这样的：

　　①将第p~第q个数同时加上x   ②求第p个数的值。

　　与之前不同的是，这里我们是把一个区间[p,q]同时加上x，怎么办呢，难道又要回到mn²的时代了吗？

　　不不不，看第②个操作，发现只需要求1个数的值，我们需要借助一种方法来变成第一道题：差分！

　　注意：这里的差分不是二分，而是An-1-An。

　　比如说这N 个整数是这样的：3   19    2   15   1   11   4   7

　　那对他们进行差分就得到了：3   16   -17   13  -14   10  -7  3

　　把[p,q]区间加上x就可以看做把差分序列的第p-1个数加x，把第q个数-x

　　而求第n个数，就可以用前缀和法了~~~~~~

　　对了，差分序列的前缀和就是原数列的第n项哦！

2（区间修改区间查询）：有N个整数，对他们进行M次操作，可能是这样的：

　　①将第p~第q个数同时加上x   ②求[p,q]的值。

　　哈哈，这下是不是难住了？我们这次再来用一用差分试一试吧。

　　已知差分序列di的前缀和Si就是原数列的第i项ai。

　　可以发现x∑i=1 ai   =   x∑i=1 i∑j=1 dj   =   x∑i=1*(x−i+1)*di(可能太深奥，解释一下：p∑i=1  xi  代表x1+x2+x3……+xp）

　　所以∑i=1xai=(x+1)∑i=1xdi−∑i=1xdi×i

　　于是我们把原数组差分后维护两个树状数组，一个维护didi，一个维护di×i就行了。

　　bye~

　　树状数组 完

PS：单击图片即可加入团队（如果您有洛谷账号的话），或者您可以注册一个