字符串学习笔记
哈希
引入:给定两个字符串 \(S\) 和 \(T\),比较他们是否本质相同。
直接比较是 \(O(n)\) 的,显然不优。为此我们引入哈希的概念:我们给每个字符串赋予一个权值,比较权值的大小即可。
那么一个字符串的权值如何得到?我们钦定基数 \(base\) 与模数 \(mod\),其中 \(base\) 为大于字符种数的较小质数,\(mod\) 为大质数(例如 \(998244353\) 和 \(1000000007\)),则权值通过以下方法得到:
显然会有一定概率错,但是正确率极高。
KMP 算法
定义:若 \(S\) 的一个前缀同时是其后缀,则这个前缀称作 \(S\) 的一个 border。
定义:称 \(S\) 有长度为 \(p\) 的周期,满足 \(S_{i}=S_{i+p}(1 \le i \le n-p)\)。
性质:
-
若 \(S_{[1,p]}\) 是 \(S\) 的 border,则其周期为 \(|S|-p\)。
-
\(S\) 的 border 的 border 也是 \(S\) 的 border。
kmp 用于字符串匹配相关问题,先抛一个最基本的问题:给定文本串 \(S\) 和模式串 \(T\),问在 \(S\) 中那些位置能匹配到模式串 \(T\)。
定义:\(\mathrm{nxt_{i}}\) 表示模式串的长度为 \(i\) 的前缀的最长 border 的长度。首先是一个个匹配,若在位置 \(j\) 遇到匹配不到的,立刻跳回上一个 \(\mathrm{nxt_{j}}\),由于前缀 border 和后缀 border 相同,后面匹配过了,所以前面的也一定可以匹配,所以直接跳回最长 border 一定最优。
放个图:
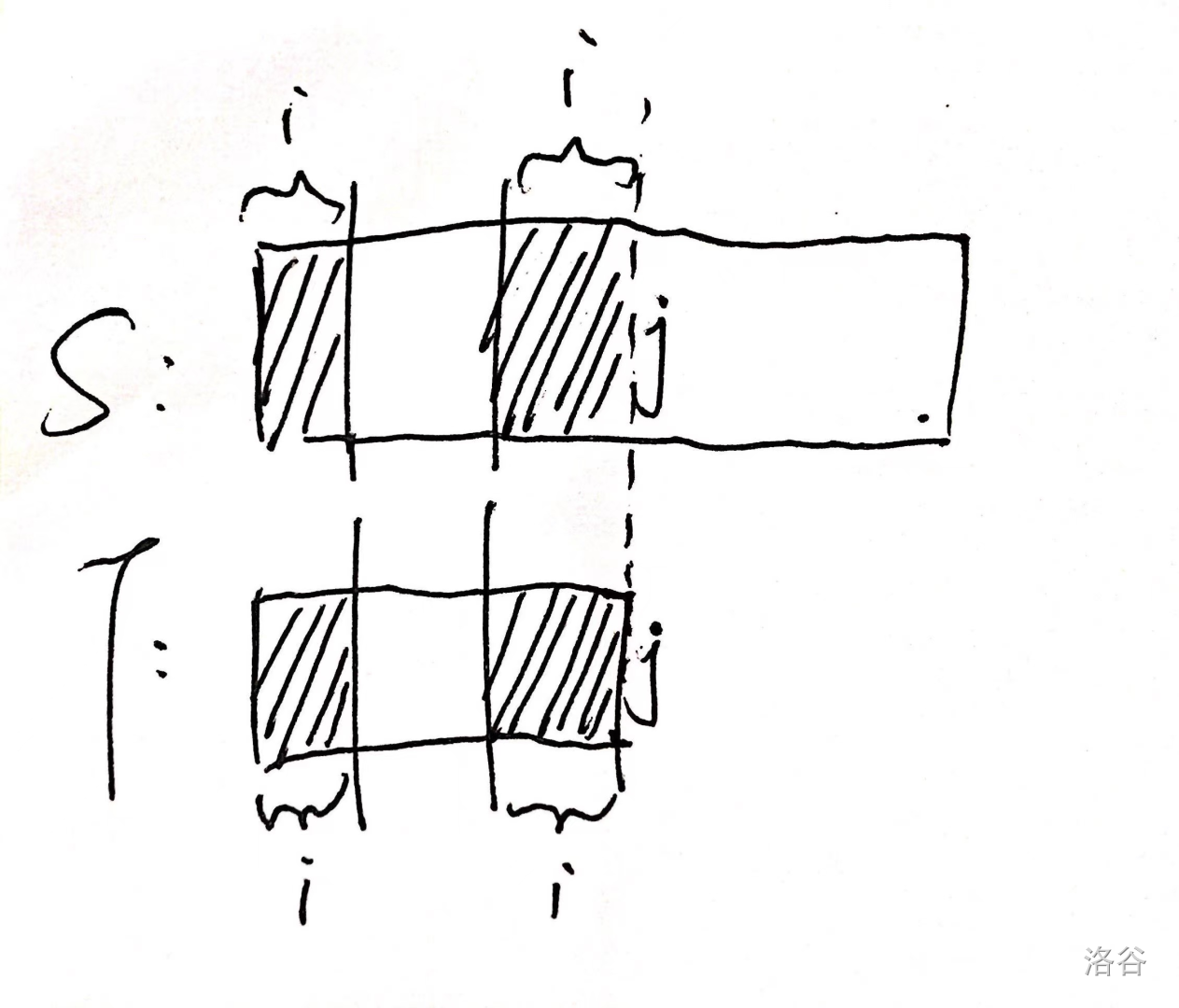
假设 \([1,j-1\)] 部分已经匹配到,而第 \(j\) 个位置不匹配,前 \(j-1\) 的最长 border 长度为 \(i\),那么下一次我不需要重新从 \(1\) 开始匹配。图中可以发现由于前 \(j-1\) 已经匹配,那么 \(T\) 的第一段和 \(S\) 的最后一段也一定相同(四块阴影都相同)。所以失配后跳到这样:
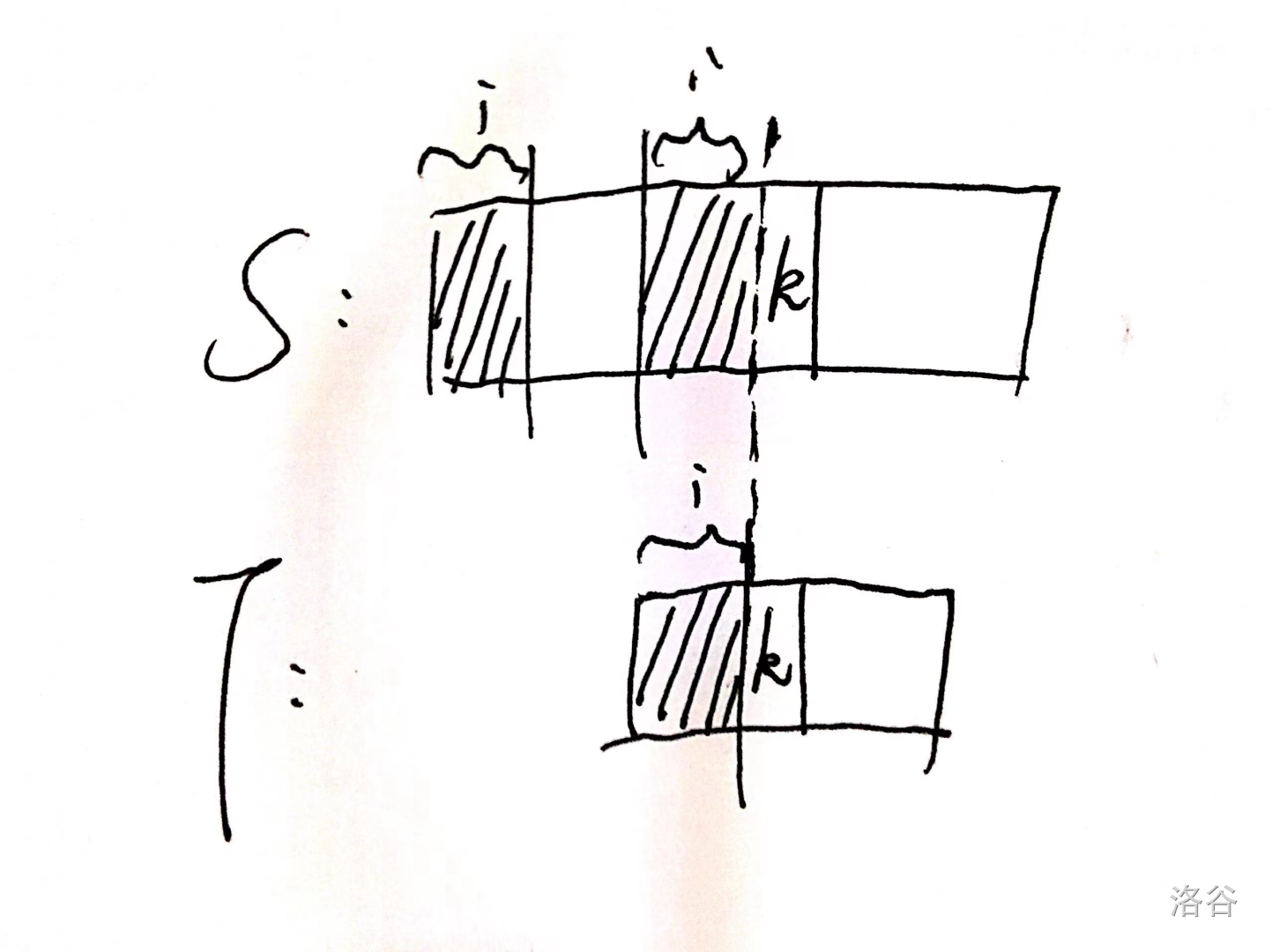
即跳到 \(k-1\) 这个位置,前面的都相同,继续匹配看第 \(k\) 个位置能否匹配,若还是失配则继续跳最长 border,跳最长的能保证在正确的前提下最大化减少时间复杂度,这里最长 border 的位置即为 \(\mathrm{nxt}\) 数组。求 \(\mathrm{nxt}\) 数组的过程可以感性理解为字符串 \(T\) 自己跟自己匹配,多画图吧。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define N 1000005
int n,m,i,j,ans,a,b,c,nxt[N];
char s[N],t[N];
int main(){
scanf("%s",s+1);
scanf("%s",t+1);
n=strlen(s+1),m=strlen(t+1);
for(i=2;i<=m;i++){
while(j && t[j+1]!=t[i]) j=nxt[j];
if(t[j+1]==t[i]) j++;
nxt[i]=j;
}
j=0;
for(i=1;i<=n;i++){
while(j && t[j+1]!=s[i]) j=nxt[j];
if(t[j+1]==s[i]) j++;
if(j==m){
printf("%d\n",i-j+1);
j=nxt[j];
}
}
for(i=1;i<=m;i++) printf("%d ",nxt[i]);
return 0;
}
很显然把下一个串当前缀,把当前串当后缀不断跑 kmp 即可,但是这样会超时,取 \(\min(|S|,|T|)\) 当前后缀即可。注意这里的 \(S\) 指的是 \(T\) 前面所有的串组成的答案。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define N 1000005
int n,m,i,j,ans,nxt[N],T,len,k,r,lst,cnt,fir,Min,x;
char s[N],t[N],pr[N],p[N];
int main(){
scanf("%d",&T);
if(T==1){
scanf("%s",s+1);
printf("%s",s+1);
return 0;
}
T--,scanf("%s",s+1),n=strlen(s+1);
while(T--){
scanf("%s",t+1),k=0,len=strlen(t+1);
cnt++,Min=min(n,len);
for(i=1;i<=Min;i++) p[++k]=t[i];
for(i=n-Min+1;i<=n;i++) p[++k]=s[i];
j=0,nxt[1]=0;
for(i=2;i<=k;i++){
while(j && p[j+1]!=p[i]) j=nxt[j];
if(p[j+1]==p[i]) j++;
nxt[i]=j;
}
x=nxt[k];
while(x>Min) x=nxt[x];
for(i=x+1;i<=len;i++) s[++n]=t[i];
}
for(i=1;i<=n;i++) printf("%c",s[i]);
return 0;
}
fail 失配树
若我们要求某个前缀的 border 个数怎么求?不断跳 \(\mathrm{nxt}\) 自然是可行的,我们也可以考虑建出失配树。
对于 \(S\) 的每个前缀 \([1,i]\),我们连一条 \((\mathrm{nxt_{i}},i)\) 的有向边,那么最终有了一棵 \(n+1\) 个节点的以 \(0\) 为根的有向树。性质:
-
对于一个点 \(i\),它的 border 集合便是它到树根的路径上的所有点对应的前缀。
-
点 \(u\) 和点 \(v\) 在 fail 树上的 lca 指的是长度分别为 \(u\) 和 \(v\) 的前缀的最长公共 border。
那么前面那个问题的答案实际就是节点的深度值。
模板题:P5829 【模板】失配树。
就是求两个前缀的最长公共 border,那么找出他们在 fail 树上的 lca 即可,复杂度 \(O(n \log n)\)。
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define N 2000005
int n,m,i,j,ans,a,b,c,k,t,p,q,nxt[N],dep[N],f[N][25],LG[N];
char s[N];
vector<int>G[N];
void dfs(int k,int lst){
dep[k]=dep[lst]+1,f[k][0]=lst;
for(int i=1;i<=LG[dep[k]];i++) f[k][i]=f[f[k][i-1]][i-1];
for(auto y:G[k]) dfs(y,k);
}
int lca(int a,int b){
if(dep[b]>dep[a]) swap(a,b);
for(int i=20;i>=0;i--){
if(dep[f[a][i]]>=dep[b]) a=f[a][i];
}
if(a==b) return f[a][0];
for(int i=20;i>=0;i--){
if(f[a][i]!=f[b][i]) a=f[a][i],b=f[b][i];
}
return f[a][0];
}
int main(){
scanf("%s",s+1),n=strlen(s+1);
LG[1]=0;for(i=2;i<=n;i++) LG[i]=LG[i-1]+((i&(-i))==i);
j=0,nxt[1]=0;
for(i=2;i<=n;i++){
while(j && s[j+1]!=s[i]) j=nxt[j];
if(s[j+1]==s[i]) j++;
nxt[i]=j;
}
for(i=1;i<=n;i++) G[nxt[i]].push_back(i);
dep[n+1]=-1;dfs(0,n+1);
scanf("%d",&t);
while(t--){
scanf("%d%d",&p,&q);
printf("%d\n",lca(p,q));
}
return 0;
}
- 这个题首先可以直接 kmp,若跑的过程中前缀长度 \(k\) 满足 \((k+1) \times 2>i\) 则及时跳 \(\mathrm{nxt}\) 即可,正确性证明有点难,这里不再赘述,复杂度 \(O(|S|+|T|)\)。代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define N 1000005
#define int long long
const int mod=1e9+7;
int n,m,i,j,ans,nxt[N],t,k,pr[N],sum,G[N],W[N],num[N];
char s[N];
signed main(){
scanf("%lld",&t);
while(t--){
scanf("%s",s+1),n=strlen(s+1),ans=1;
memset(nxt,0,sizeof(nxt));
memset(num,0,sizeof(num));
j=0,nxt[1]=0,num[1]=1;
for(i=2;i<=n;i++){
while(j && s[j+1]!=s[i]) j=nxt[j];
while(k && (s[k+1]!=s[i] || (k+1)*2>i)) k=nxt[k];
if(s[j+1]==s[i]) j++;
if(s[k+1]==s[i]) k++;
nxt[i]=j,num[i]=num[nxt[i]]+1;
ans=(ans*(num[k]+1))%mod;
}
if(t!=0) printf("%lld\n",ans);
else printf("%lld",ans);
}
return 0;
}
- 稍微无脑的做法我们可以考虑建立失配树,对于每个节点,我们只需在失配树上用倍增找出最大的 border 长度满足 \(2 \times k \le i\),记为节点 \(p\),那么答案乘上 \(dep_{p}+1\) 即可,复杂度 \(O(|S| \log |S|)\),跑步过去,但是只需要
玄学把倍增数组两个维度反过来即可 AC。代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define N 2000005
#define int long long
const int mod=1e9+7;
int n,m,i,j,ans,a,b,c,k,t,p,q,nxt[N],dep[N],f[25][N],LG[N],u[N],h[N];
char s[N];
struct AB{
int a,b,n;
}d[N];
void cun(int a,int b){
d[++k].a=a,d[k].b=b;
d[k].n=h[a],h[a]=k;
}
queue<int>Q,L;
void bfs(int k){
Q.push(k),L.push(n+1);
while(!Q.empty()){
a=Q.front(),Q.pop(),b=L.front(),L.pop(),f[0][a]=b;
for(int i=1;i<=LG[dep[a]];i++) f[i][a]=f[i-1][f[i-1][a]];
for(int i=h[a];i;i=d[i].n){
int b=d[i].b;
dep[b]=dep[a]+1;
Q.push(b),L.push(a);
}
}
}
int get(int Y,int x){
for(int i=LG[dep[x]];i>=0;i--){
if(f[i][x]*2>Y) x=f[i][x];
}
return dep[f[0][x]];
}
signed main(){
scanf("%lld",&t);
while(t--){
for(i=0;i<=n+1;i++) h[i]=0;
for(i=0;i<=n+1;i++){
for(j=0;j<=20;j++) f[j][i]=0;
}
scanf("%s",s+1),n=strlen(s+1),ans=1,k=0;
LG[1]=0;for(i=2;i<=n;i++) LG[i]=LG[i-1]+((i&(-i))==i);
j=0,nxt[1]=0;
for(i=2;i<=n;i++){
while(j && s[j+1]!=s[i]) j=nxt[j];
if(s[j+1]==s[i]) j++;
nxt[i]=j;
}
for(i=1;i<=n;i++) cun(nxt[i],i);
cun(n+1,0);
dep[n+1]=-1,bfs(n+1);
for(i=1;i<=n;i++){
int p=get(i,i);
ans=(ans*(p+1))%mod;
}
if(t!=0) printf("%lld\n",ans);
else printf("%lld",ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号