P3376 网络流 Dicnic+当前弧优化

【模板】网络最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入格式

第一行包含四个正整数 \(n,m,s,t\)，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来 \(m\) 行每行包含三个正整数 \(u_i,v_i,w_i\)，表示第 \(i\) 条有向边从 \(u_i\) 出发，到达 \(v_i\)，边权为 \(w_i\)（即该边最大流量为 \(w_i\)）。

输出格式

一行，包含一个正整数，即为该网络的最大流。

样例 #1

样例输入 #1

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 30

样例输出 #1

50

提示

样例输入输出 1 解释

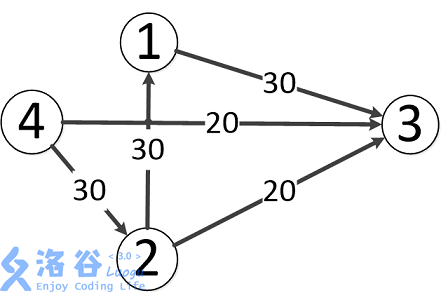
题目中存在 \(3\) 条路径：

• \(4\to 2\to 3\)，该路线可通过 \(20\) 的流量。
• \(4\to 3\)，可通过 \(20\) 的流量。
• \(4\to 2\to 1\to 3\)，可通过 \(10\) 的流量（边 \(4\to 2\) 之前已经耗费了 \(20\) 的流量）。

故流量总计 \(20+20+10=50\)。输出 \(50\)。

---

数据规模与约定

• 对于 \(30\%\) 的数据，保证 \(n\leq10\)，\(m\leq25\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n\leq200\)，\(1 \leq m\leq 5000\)，\(0 \leq w\lt 2^{31}\)。

Dicnic

注意 cnt=1!

bfs中和SPFA 类比来写

当前弧优化可以 大大大大大 提高速率！！！！ 2.…s ---> 60ms！

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e4+5;
int n,m,s,t;
struct Graph{
	int nxt,to,val,from;
}edge[N<<1];
int head[N],cnt=1;//cnt=1 ! 
inline void add(int u,int v,int w)
{
	cnt++;
	edge[cnt].to=v;
	edge[cnt].nxt=head[u];
	edge[cnt].val=w;
	edge[cnt].from=u;
	head[u]=cnt;
}
int dep[N],inque[N],cur[N];
bool bfs()//分层
{
	for(int i=1;i<=n;i++)
	{
		dep[i]=LONG_LONG_MAX;
		inque[i]=0;
		cur[i]=head[i];
	}
	dep[s]=0;
	queue<int>q;
	q.push(s);
	inque[s]=1;
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		inque[u]=0;//同SPFA一样 要将取出的元素的inque(vis)[]置为零 
		for(int i=head[u];i;i=edge[i].nxt)
		{
			int v=edge[i].to;
			if(dep[v]>dep[u]+1&&edge[i].val!=0)
			{
				dep[v]=dep[u]+1;//分层 
				if(!inque[v])//同SPFA 
				{
					q.push(v);
					inque[v]=1;
				}
			}
		}
	}
	if(dep[t]!=LONG_LONG_MAX)return 1;//说明对于S--->T都能分好层 说明还有增广路
	return 0; 
} 
int dfs(int u,int flow)//u:当前点   flow:当前增广路径上的最小边权
{
	int rlow=0;
	if(u==t)return flow;//已经到达t点了
	for(int i=cur[u];i;i=edge[i].nxt)
	{
		cur[u]=i;		
		int v=edge[i].to;
		if(edge[i].val!=0&&dep[v]==dep[u]+1)
		{
			if(rlow=dfs(v,min(flow,edge[i].val)))
			{
				edge[i].val-=rlow;//正向边 - rlow
				edge[i^1].val+=rlow;//反向边 + rlow
				return rlow; 
			}
		}
	} 
	return 0;//无法到达t 无增广路 
} 
int maxflow=0;
int Dicnic()
{
	int flow;
	while(bfs()!=0)
	{
		while(flow=dfs(s,LONG_LONG_MAX))
			maxflow+=flow;
	}
	return maxflow;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m>>s>>t;
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		cin>>u>>v>>w;
		add(u,v,w);
		add(v,u,0);
	}
	cout<<Dicnic()<<"\n";
	return 0;
}