4.18 maths 复变函数 留数部分总结

首先补充关于零点 极点的相关概念及结论

零点

极点

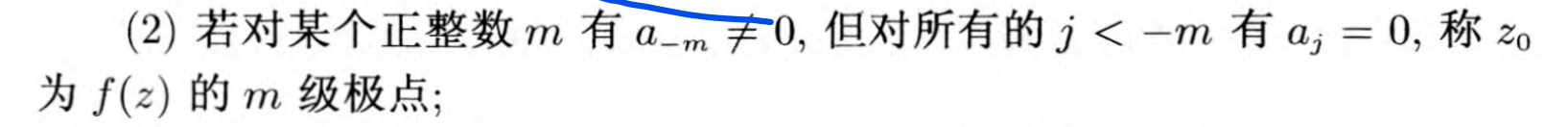
可以看出零点和极点有着密切的关系(可以理解为互逆)

留数

留数定义

留数定理

留数计算

实用技巧

但是要注意所有的非∞的孤立奇点都要在解析域内 像后面取上半圆周等就不能这么算

因此我们可以将 Σ 转化为 求∞点处的留数

∞点留数的计算

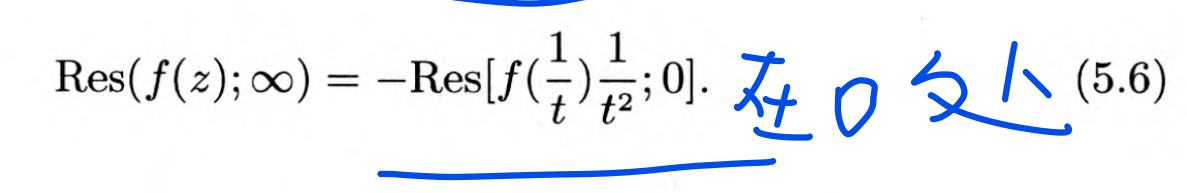
留数在实积分计算中的应用

[0,2Π]上的三角积分

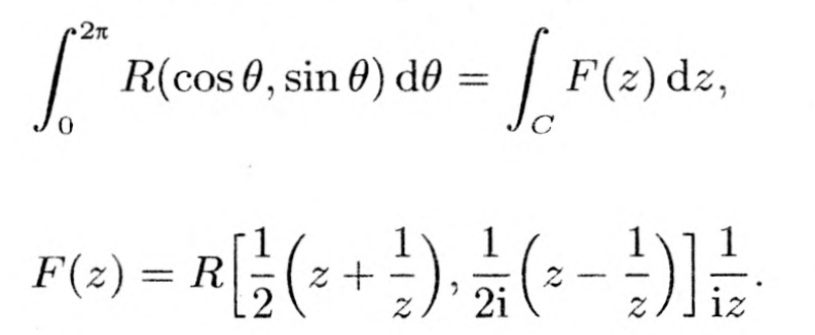
(-∞,+∞)上函数的广义积分

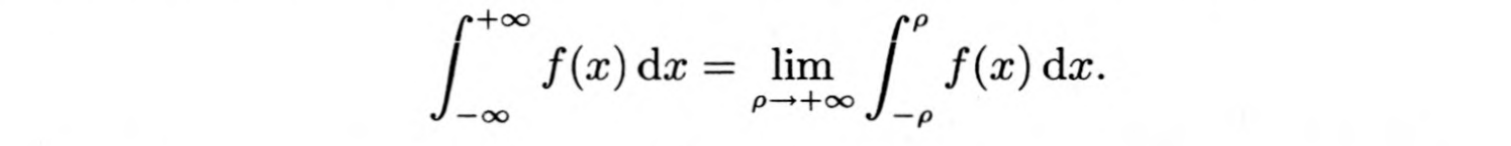
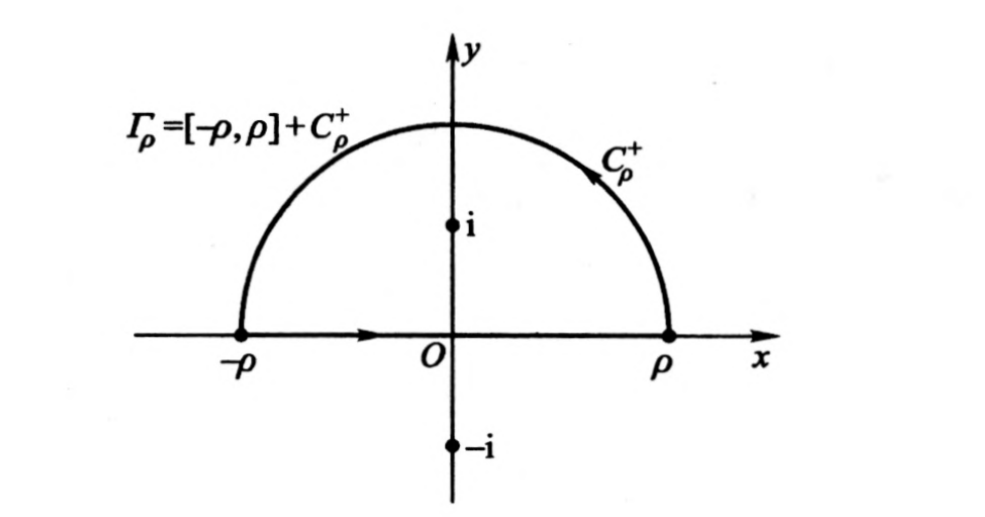
因此 -ρ -> +ρ = ∫Cη = 2Πi×ΣRes( ,Xi) Xi∈上半圆周C

三角函数的广义积分

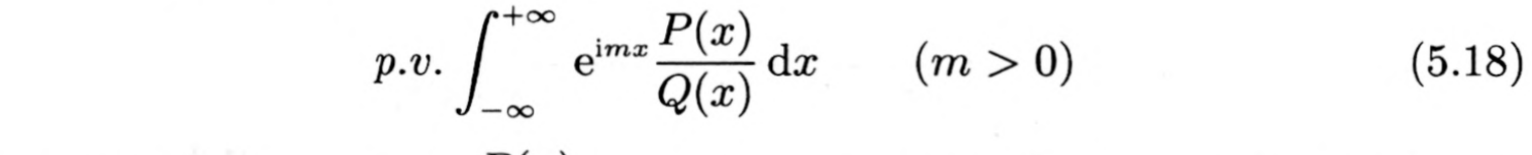
因此 用 exp(iz)将三角函数替换掉 对 m>0 m<0 分别用若尔当引理求 = 2Πi×ΣRes(,Xi) Xi∈上半圆周 ……∈下半圆周 即可

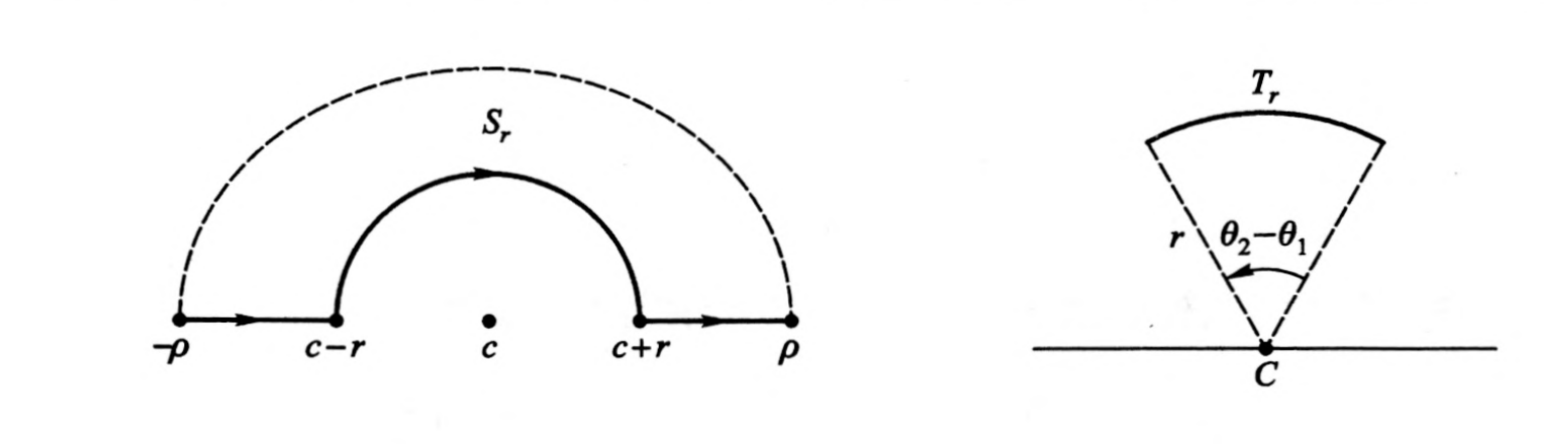
积分路径上有奇点的积分

取逆时针为正向 三部分构成

-ρ -> -r +r - > +ρ 是我们要求的

-r -> +r 的小圆周我们由引理可求

上半圆周积分为0(能求肯定是0🤣)

总的闭合曲线积分 由于我们将奇点(可能有多个 那么我们就取多个 -r>+r类型的小圆周)排除了 所以闭合曲线解析 因此由柯西积分定理知 ∫ ≡ 0

所以我们就能求出来了

总结：降维打击