P3386 二分图最大匹配 匈牙利算法

【模板】二分图最大匹配

题目描述

给定一个二分图，其左部点的个数为 \(n\)，右部点的个数为 \(m\)，边数为 \(e\)，求其最大匹配的边数。

左部点从 \(1\) 至 \(n\) 编号，右部点从 \(1\) 至 \(m\) 编号。

输入格式

输入的第一行是三个整数，分别代表 \(n\)，\(m\) 和 \(e\)。

接下来 \(e\) 行，每行两个整数 \(u, v\)，表示存在一条连接左部点 \(u\) 和右部点 \(v\) 的边。

输出格式

输出一行一个整数，代表二分图最大匹配的边数。

样例 #1

样例输入 #1

1 1 1
1 1

样例输出 #1

1

样例 #2

样例输入 #2

4 2 7
3 1
1 2
3 2
1 1
4 2
4 1
1 1

样例输出 #2

2

提示

数据规模与约定

对于全部的测试点，保证：

• \(1 \leq n, m \leq 500\)。
• \(1 \leq e \leq 5 \times 10^4\)。
• \(1 \leq u \leq n\)，\(1 \leq v \leq m\)。

不保证给出的图没有重边。

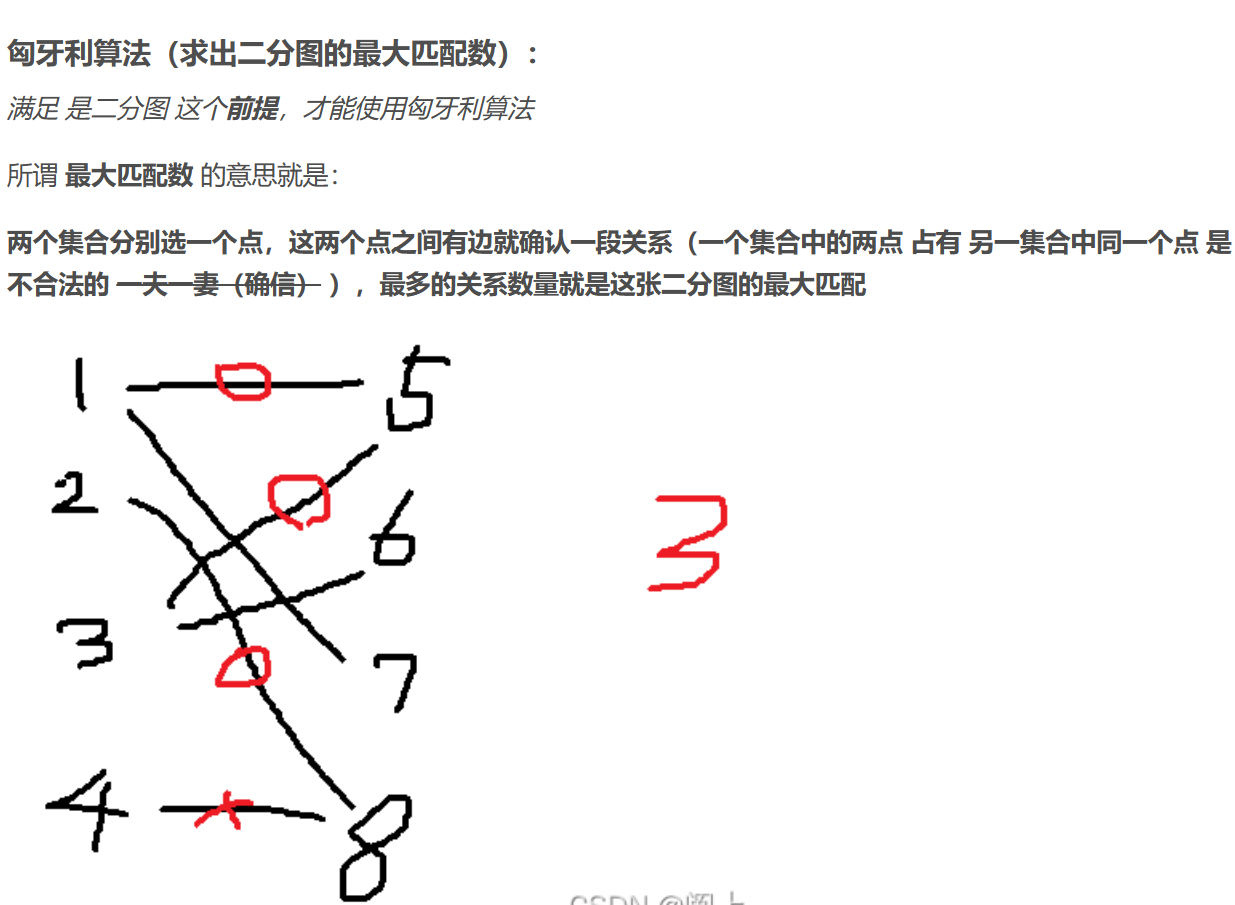
匈牙利算法

几个数组含义：

vis[]: 对于每个左边集合的点 每次清空vis[] 标记右边集合的点是否访问过 防止重复访问
match[]: 右边集合的每个点 匹配的左边集合的点
算法

核心思想

如果i没有匹配对象 或者 i的匹配对象v可以找到另外的匹配对象 那么x就可以和i匹配

注意不止一个连通块 即 一次染色不一定染完了 所以要遍历1~n 判断col[i]==0?

#include<bits/stdc++.h>
using namespace std;
//二分图最大匹配 匈牙利算法
#define int long long
int n,m,e;
int g[505][505]; 
int vis[505],match[505];//match 记录的是 右边集合匹配的点 
bool find(int x)
{
	for(int i=1;i<=m;i++)
		if(!vis[i]&&g[x][i])//如果存在边 且 没有标记过
		{
			vis[i]=1;//标记防止重复访问 
			int v=match[i];
			if(v==0||find(v))//如果i没有匹配对象 或者 i的匹配对象v可以找到另外的匹配对象
							// 那么x就可以和i匹配
			{
				match[i]=x;
				return true;//x找到了匹配对象 
			}
		}
	return false;//x没找到匹配对象
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m>>e;
	for(int i=1;i<=e;i++)
	{
		int u,v;
		cin>>u>>v;
		g[u][v]=1;
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(find(i))ans++;
	}
	cout<<ans<<"\n";
	return 0;
}