C++ 浅谈平行四边形不等式优化DP
前言
在区间DP中,第三重循环枚举分割点容易造成超时,那么又什么方法来优化呢?
当然有,有一种叫做平行四边形不等式的玩意优化DP
平行四边形不等式
如果有两个区间满足 f[a][c]+f[b][d]<=f[b][c]+f[a][d],那么这个东东就是平行四边形不等式
可以这样理解,交叉或包含的两个区间,a到c和b到d的值满足小于等于包含的两个区间(bc被包含于ad)
还有就是决策单调性
w[i,j]<=w[i',j'] ([i,j]属于[i',j']) 既 i'<=i<j<=j'
平行四边形不等式的性质
这玩意儿有什么性质,对边互相平行?
非也,这玩意儿有两个性质
定义一个 动态转移方程 f[i][j] = min( f[i][j] , f[i-1][k]+w[k-1][j] )
一. 如果w满足决策单调性 且满足平行四边形不等式那么 f 也满足四边形不等式
二. 当定理一的条件满足时,让f [ i ][ j ]取最优值的minx为minx[ i , j ],则minx[ i - 1 , j ] <= minx[ i , j ] <= minx[ i , j + 1 ] </


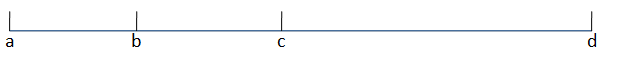

 浙公网安备 33010602011771号
浙公网安备 33010602011771号