题解：P11662 [JOI 2025 Final] 方格染色 / Grid Coloring

题目传送门

是一道黄题
这里提供一种 \(O(n\log n)\) 的做法

---

\(\mathscr{PART\ \ ONE}\)

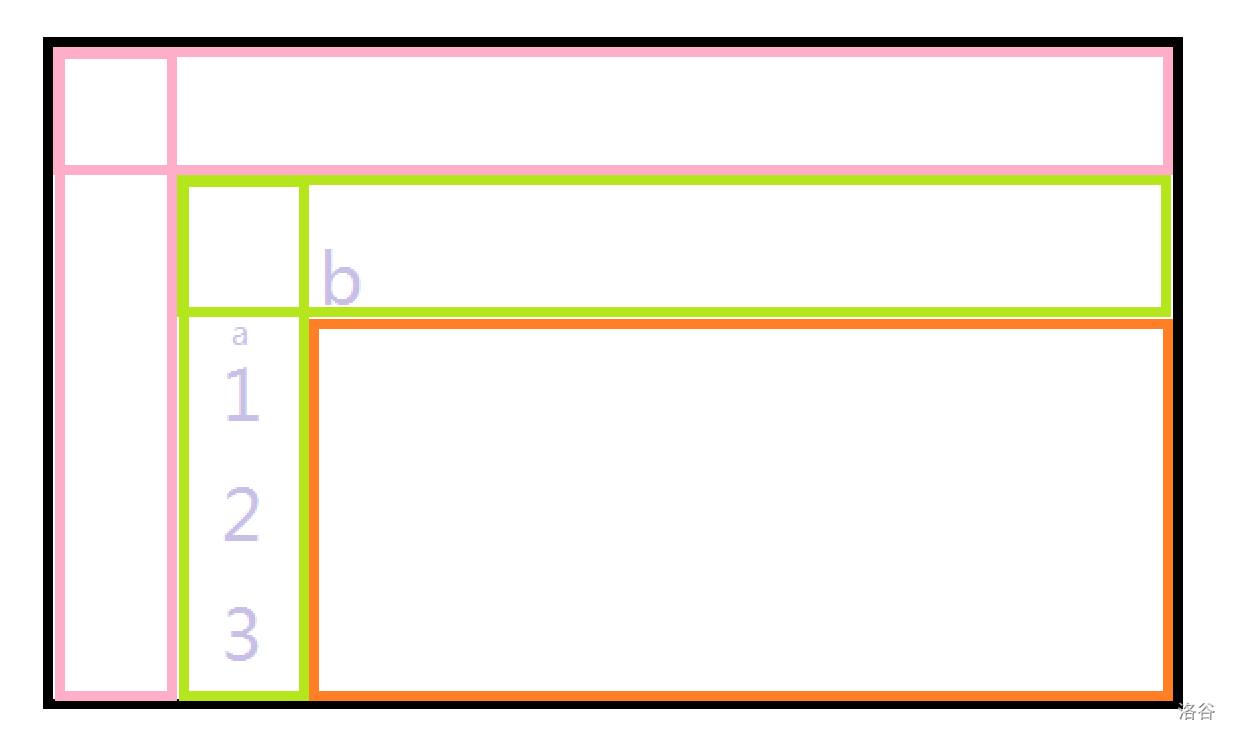
我们在手%的时候不难发现（注意力有点也不惊人）
虽然第一列和第一行 不保证有序
但是因为这里的前缀$\ max\ $性质保证了第二列和第二行有序
我们很容易用 \(O(n)\) 把他们求出来
定义这两个数组为 \(a_i\) 、\(b_i\)

---

\(\mathscr{PART\ \ TWO}\)

我们缩小范围，只观察这些绿色和橙色的区域，
发现 \(a_i\) 、 \(b_i\) 单调递增，
考虑对于每个 \(a_i\) 我们在 \(b_i\) 里面找到小于它的一段。
这里也不用想太多，
直接使用lower_bound就可以解决
详细的代码可能有点难调（我也不知道为什么）（反正我调了很久）
然后对于其他部分，
我们开个数组差分，最后一遍的时候再处理就好了
$\ $
（小声嘟囔）其实就是暴力想法加上了一堆优化

---

\(\Huge \mathbb{CODE}\)
已经按照GOOGLE标准格式化

---

#include<bits/stdc++.h>
#define int long long
using namespace std;
#define f(a,b,c) for(int a=b;a<=c;a++)
#define ft(a,b) for(auto a:b)

const int N=2e5+10;
int n;
int A[N];
int B[N];
int a[N];
int b[N];
int cf[N];
map<int,int>mp;

main(void){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);cout.tie(nullptr);
	
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>A[i];
		if(i==1)continue;//spj
		mp[A[i]]++;
	}
	for(int i=1;i<=n;i++){
		cin>>B[i];
		mp[B[i]]++;
	}
	
	b[1]=A[2];
	for(int i=2;i<=n;i++){
		b[i]=max(b[i-1],B[i]);
		mp[b[i]]++;
	}
	a[1]=B[2];
	for(int i=2;i<=n;i++){
		a[i]=max(a[i-1],A[i]);
		if(i==2)continue;//spj
		mp[a[i]]++;
	}
	
	for(int i=3;i<=n;i++){
		int pos=lower_bound(b+3,b+n,a[i])-b;
		if(a[i]<b[pos])pos--;
		mp[a[i]]+=pos-3+1;
		cf[pos+1]++;
	}
	
	for(int i=3;i<=n;i++)cf[i]+=cf[i-1];
	for(int i=3;i<=n;i++)mp[b[i]]+=cf[i];
	
	int id=A[1],ans=mp[A[1]];
	
	for(int i=2;i<=n;i++){
		if(mp[A[i]]>ans)id=A[i],ans=mp[A[i]];
		else if(mp[A[i]]==ans)id=max(id,A[i]);
		
		if(mp[B[i]]>ans)id=B[i],ans=mp[B[i]];
		else if(mp[B[i]]==ans)id=max(id,B[i]);
	}
	cout<<id<<' '<<ans<<endl;
}
//[JOI 2025 Final] 方格染色