Noivelist

摘要：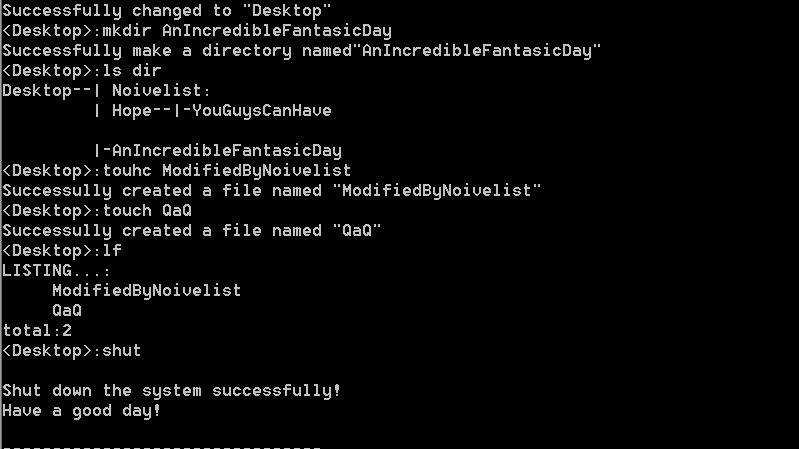

upd:2025/10 初步完成了虚拟的文件夹及文件目录管理，主要功能有：创建虚拟文件夹、显示路径、创建文件、列出当前路径下文件（夹）、转到特定目录。 upd:2025/11/19 初步实现了与 \(\operatorname {windows}\) 的真实接口，现在可以真实地在该 \(\opera 阅读全文

posted @ 2025-11-24 21:09 Noivelist 阅读(43) 评论(0) 推荐(0)

[置顶] 自己的火印

摘要： /** * Modified by Noivelist, * Luogu:https://www.luogu.com.cn/user/700335 * Marsoj:http://marsoj.com/user/252 * “倘若梦境醒来，执念破去，我们再谈救赎” * Working on Proj 阅读全文

posted @ 2025-11-06 18:58 Noivelist 阅读(10) 评论(0) 推荐(0)

2026年1月17日

挂机放置类游戏开发学习 Part.3 UI布局

摘要： UI 布局阶段核心目标回顾（落地挂机游戏）搭建双窗口：「挂机游戏主面板」（核心功能，保留原有数值 / 按钮 / 进度条）+「游戏设置面板」（新增，调整挂机参数、UI 样式）；掌握分组布局：用分组、折叠面板分隔不同功能区域，避免 UI 拥挤；掌握行列布局：用多列排版让数值和组件对齐，提升美观度；阅读全文

posted @ 2026-01-17 17:16 Noivelist 阅读(13) 评论(0) 推荐(0)

挂机放置类游戏开发学习 Part.2 基础组件

摘要：恭喜你成功完成环境搭建并运行出预期效果！这是一个非常棒的里程碑，现在完全可以顺利进入《基础组件》阶段了，这个阶段的核心是掌握 ImGUI 的 \(3\) 个核心基础组件（Text、Button、ProgressBar），并落地到挂机游戏的核心数值展示与简单交互，咱们一步步推进，全程基于你现有的代码扩阅读全文

posted @ 2026-01-17 16:38 Noivelist 阅读(5) 评论(0) 推荐(0)

2026年1月12日

挂机放置类游戏开发学习历程

摘要： \(\Large \mathcal{ImGUI}\) 我准备以 \(C++\) 为核心（也只用 \(C++\) ）来完成这一学习流程，先要学习的是 ImGUI 这一前端库。使用 AI 生成了一份可能需要的学习流程图。阶段学习目标（核心）具体落地要求（适配挂机游戏）环境搭建完成 ImGUI 阅读全文

posted @ 2026-01-12 12:26 Noivelist 阅读(10) 评论(0) 推荐(0)

2025年11月28日

题解：P1471 方差

摘要：【题目传送门】一眼分块能做，然后就来开始做。狠狠地做。构造我们考虑根号分治，对于每个块我们开：当前的数值和 \(sum1\)，当前的数值平方的和 \(sum2\)，当前的数值的 \(\operatorname {lazy}\) 数组。这道题最阴险的地方是它的输入不是全部整数，但是样例给的是正阅读全文

posted @ 2025-11-28 11:16 Noivelist 阅读(8) 评论(0) 推荐(0)

题解：P1273 有线电视网 - 树形背包DP

摘要：【题目传送门】本题解是对洛谷题解https://www.luogu.com.cn/article/t5t4lx51的再阐述 & 学习笔记。这里是这个 \(\mathcal {O(nm)}\) 的时间复杂度的做法：我们看到题目不难想到写一个树形背包 DP，很显然这就是裸题。我们设 \(f_{i 阅读全文

posted @ 2025-11-28 10:15 Noivelist 阅读(14) 评论(0) 推荐(0)

2025年11月27日

题解：P8398 [CCC 2022 S4] Good Triplets

摘要：【题目传送门】题意分析：给定一个圆和圆周上均匀分布的点，求能包括圆心的三角形的数量。每个点都有编号，点可以重叠，不同编号的点形成的相同形状的三角形视为不同的三角形。很明显的一个事情是，如果我们构成的三角形的某两个点在同一个位置，这明显不是三角形，而退化成了点或者线。这题和计算几何没有任何关阅读全文

posted @ 2025-11-27 15:15 Noivelist 阅读(10) 评论(0) 推荐(0)

2025年11月26日

题解：B4374 [GXPC-S 2025] 花 / flower

摘要：题目传送门题意大致理解：我们要维护一棵树，支持树上的单点修改，和子树的区间查询。题意推敲：单点查询不在话下，我们需要区间查询用数据结构去维护的话没有一个好的、简单的树上结构来维护他。那么我们可以根据这个子树这个性质来把这个树上转化为线性的数据结构问题。不难想到 DFS 序，一个节点 &u& 阅读全文

posted @ 2025-11-26 15:21 Noivelist 阅读(8) 评论(0) 推荐(0)

2025年11月21日

题解：NFLSOI#P10008. Speike和Tom

摘要：众所周知，Speike 狗是一条特别喜欢追着 Tom 打的狗。现在，Tom 又把 Speike 惹生气了，现在 Speike 需要跨越千山万水找 Tom 报仇。 Speike 所在的世界可以看成是一个无穷大的平面，平面由一个平面直角坐标系确定。在平面上有许多不相交的矩形障碍，矩形的四边平行于坐标轴阅读全文

posted @ 2025-11-21 15:40 Noivelist 阅读(21) 评论(0) 推荐(0)

题解：NFLSOI#31351. 小吃

摘要：题面： Shor 小鸭已经准备了 \(n\) 个小吃盘子，准备一边看电影一边享用！第 \(i\) 个盘子最初装有一个美味值为 \(a[i]\) 的小吃。你需要处理 \(q\) 个查询。在第 \(j\) 个查询中，Shor 将按顺序执行以下两个操作： 1. 吃掉所有美味值在 \(l[j]\) 到 \ 阅读全文

posted @ 2025-11-21 15:01 Noivelist 阅读(7) 评论(0) 推荐(0)

小窝

公告