3 月做题记录
3.1-3.9
P1587 [NOI2016] 循环之美
首先考虑枚举循环节长度,则 \([\frac {xk^l}y]=[\frac x y]\),所以:
所以
边界是 \(k=1\) 或者 \(n=0\) 或者 \(m=0\),然后递归,似乎复杂度是 \(O(\sqrt n\log n\log m+n^{\frac 2 3})\) 的。
P3523 [POI 2011] DYN-Dynamite
二分,然后贪心计算。
P3773 [CTSC2017] 吉夫特
lucas 拆一下,每次从超集转移过来,由于数互不相同,复杂度是对的。
P11831 [省选联考 2025] 追忆
叮咚鸡叮咚鸡,大狗大狗叫叫叫。
考虑分块维护 \(a,b\),然后我们可以扫描一遍找到 \(b\) 答案的所在值域块,然后扫一遍即可。
为了快速 check,需要手写 Bitset。
P6749 『MdOI R3』Yoshino
对于每个连续段,把权值段挂在连续段的开头即可,树套树维护。
odt 分裂的时候记得树套树上修改连续段,记得 assign 的时候先 split(r+1)。
AT_agc055_d [AGC055D] ABC Ultimatum
找必要性质,发现 \(\max (cnt_A-cnt_C)\le cnt_{ABC}\),所以我们得到:
可以证明这是充要的,然后就可以简单 \(O(n^6)\) dp 了。
CF1817F Entangled Substrings
震撼人心的基本子串结构。
对于每个等价类分开考虑
UOJ752 【UNR #6】Border 的第五种求法
UOJ577 【ULR #1】打击复读
UOJ772 【UER #11】企鹅游戏
3.10-3.31
由于电脑爆了导致丢失了部分题解,所以有些题会被删除。
P8114 [Cnoi2021] 六边形战士

(这个和原题的三角形朝向不同),把匹配的三角形按横着和两种斜着匹配的方式分成三种,染上不同颜色,发现可以看成一个三维的情况的正方体堆叠问题。
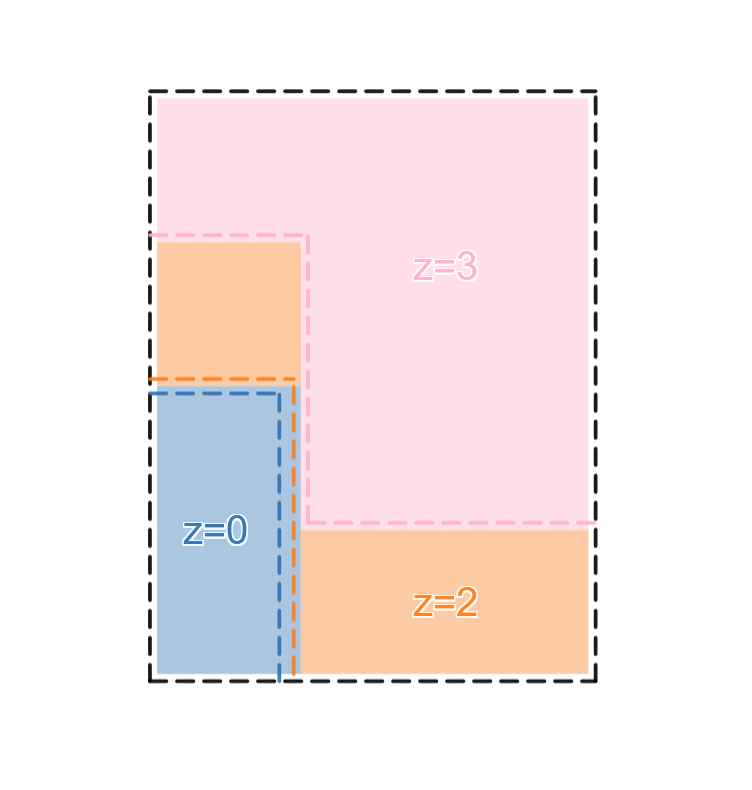
然后可以发现按值域分层,那么每层的线不能跨过。
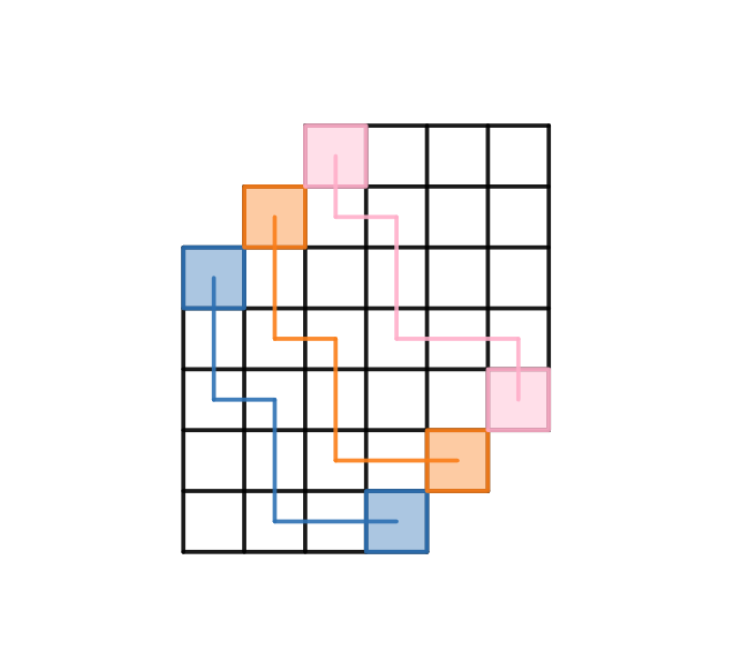
平移一下,变成格路计数的形式,然后可以推 LGV。
或者我们直接考虑对于一个 \(n\times m\) 的矩形填数,每个位置填的是这个位置的高度 \(h_{i,j}\),需要满足每行每列非严格递增,我们令 \(h'_{i,j}\gets h_{i,j}+i\),且 \(h_{i,j}\in [1,a+c]\),那么此时是个半标准杨表,根据 2019 年集训队论文内容,可以得到计算公式。
半标准杨表是列严格递增,行非严格递增的杨表。对于半标准杨表的计数有如下的公式。
若表内数为 \([1,n]\) 中的整数,那么半标准杨表 \(\lambda =(\lambda_1,\ldots \lambda_m)\) 的个数为。\[\prod_{(i,j)\in \lambda} \frac {n+j-i}{h_{\lambda}(i,j)} \]
这里略去证明,然后就可以推一下式子计算。
P6758 [BalticOI 2013] Vim
似乎是发现每条线段只会被经过不超过 \(3\) 次,有最多两次是往后跳跃,所以可以维护这两者,然后计算。
AT_agc049_e [AGC049E] Increment Decrement
日了,我原来写的题解找不到了,直接考虑按值域分层然后 dp of dp,复杂度 \(O(n^5)\)。
AT_agc048_d [AGC048D] Pocky Game
似乎是 \(L_{i,j},R_{i,j}\) 表示第一次是左/右操作的时候,至少 \(a_{i}\)/\(a_{j}\) 需要是多少才能获胜,然后区间 dp,\(O(n^2)\)。
P3561 [POI 2017] Turysta
竞赛图缩点是若干条链,然后每个 SCC 内部容易 \(O(n^2)\) 构造哈密尔顿环,本来这里应该有个带图示的详细说明,但是电脑爆炸找不到了,就不写了。
P4233 射命丸文的笔记
计算总和,除以方案数。
总和计算是简单的。
然后分母,考虑竞赛图缩点后是一条链,所以 \(G=\text{SEQ}(F)\),而 \(G\) 是任意一个竞赛图的 GF,所以得到 \(G=\frac 1{1-F},F=1-G^{-1}\)。
P3196 [HNOI2008] 神奇的国度
P3852 [TJOI2007] 小朋友
P4465 [国家集训队] JZPSTR
以上三个题都是弦图,求出完美消除序列,然后随便搞搞即可。
P8496 [NOI2022] 众数
绝对众数可以摩尔投票求出,序列合并可以线段树合并+摩尔投票。
当然不用摩尔投票可以拆位,维护二进制每一位的和,然后只有 \(0/1\) 超过一半的才可能成为答案。
然后 unordered_map 维护,似乎这个空间常数比线段树合并小,所以可以开 deque 做启发式合并。
P6775 [NOI2020] 制作菜品
考虑 \(m\ge n-1\) 的情况,每次选择最小和最大,可以归纳知道一定合法。
然后考虑 \(m=n-2\),此时只要存在一种方式,分成两个 \(m=n-1\) 的情况即可,那么这是一个可行性背包,可以 bitset 维护。
原来模拟赛做过不给定 \(k\),然后询问 \(m\) 最小为多少的题目,这种情况就需要状压 dp 了。
似乎偏序了这个题?
P7906 [Ynoi2005] rpxleqxq
莫队二离,然后需要 \(O(\sqrt V)\) 加入一个数,\(O(1)\) 询问和多少个数 xor \(\le X\),\(X\) 是一个固定常数。
这个考虑前 \(\frac 1 2\log V\) 位可以直接打 tag,后 \(\frac 1 2\log V\) 位影响到的部分也可以直接打 tag。
P4631 [APIO2018] 选圆圈
考虑按最大圆直径作为边长分块,然后每次扫周围的块即可,最大圆直径减少一倍就重构,似乎可以证明复杂度是对的。
P4244 [SHOI2008] 仙人掌图 II
仙人掌上 dp 板子,每次考虑上传什么和环怎么计算即可。
P5298 [PKUWC2018] Minimax
直接线段树合并,或者可以按值域扫描然后做 ddp 计算方案数。
P3290 [SCOI2016] 围棋
考虑计算不存在模板的情况,然后轮廓线 dp,然后用 KMP 维护当前作为第二行匹配到了哪里,发现是 \(O(Tnm3^mc)\) 云云,比较倒闭。
然后我们发现 \(O(3^m)\) 太唐了,我们可以只状压哪些地方是否倒闭,而不是具体的,这样我们同时维护当前作为第一行和第二行匹配到了哪里即可,复杂度 \(O(Tnm2^{m-c+1}c^2)=O(Tnm2^m)\),随便过。
P6108 [Ynoi2009] rprsvq
妈的怎么这个丢失了,草了,直接看这篇吧
核心大概是 \(\frac 1{k+1}=\int_0^1 x^k\mathrm d x\)。
AT_dwacon6th_prelims_e Span Covering
一个做法是钦定不能选后容斥,然后拆式子后 dp 云云,这个也是我一开始的做法。
然后另外一个做法是连续段 dp,从大到小考虑线段,不会出现覆盖之前线段的情况,然后就可以 dp 了。
P8996 [CEOI 2022] Abracadabra
似乎是看成若干前缀最大值,每个最大值连同到下一个最大值之间的数看成一个连续段,然后随便分裂一下即可,似乎挺好写的。
P8947 Angels & Demons
建出广义 SAM,然后考虑什么时候有贡献。
- 在子树内部,且不在这个节点上。
- 在这个节点上,且子串长度不大于模式串当前前缀匹配的 \(L\)。
前者直接 BIT 维护,后者每个点维护平衡树,然后询问时二分即可。
P7274 草地
有点复杂的整体二分,容易把复杂度写假。
P5333 [JSOI2019] 神经网络
首先 dp 出每棵树划分成 \(k\) 条链的方案树,然后问题是不能相邻,列出 EGF,然后容斥相邻的有多少个即可,然后从 \(1\) 出发,那么钦定这条链开头,然后容斥掉第 \(1\) 棵树的链作为最后的情况即可。
P7408 [JOI 2021 Final] 地牢 3 / Dungeon 3
不错的题目,先判断无解,对于维护后缀询问怎么办,单调栈拆一拆,然后讨论询问的油箱大小 \(U\),和弹出的 \(x\),以及剩下的 \(y\) 的贡献,发现是一次函数形式,BIT 维护。
然后我们由于询问的是区间,发现我们一定会在距离 \(r\le U\) 的最便宜的地方 \(x\) 加油,然后就可以拆成 \(ans_l-ans_x+b_x(r-x)\)。
P11173 「CMOI R1」We Want To Run / Nilpotent
首先我们只关心一个位置是不是零,然后我们考虑令 \(A\) 为一个邻接矩阵考虑问题。
那么 \(f(A)\not =0\) 等价与有边且是一个 DAG,然后我们可以考虑 dp。
然后我们跟 DAG 容斥一样,考虑按层 dp,这样似乎就可以做到 \(O(n^4)\)。
考虑我们的问题是我们在 \(i\) 层的时候,最后统计答案带上一个 \(i\),我们可以组合意义,然后在这 \(i\) 层里面选一层即可做到 \(O(n^3)\)。
P11613 [PA 2016] 覆盖 / Pokrycia
P11927 [PA 2025] 重金属 / Heavy Metal
我们可以把 meet in middle,分成两段不超过 \(\sqrt V\) 的路径,然后中间找一条边拼起来。
P6646 [CCO 2020] Shopping Plans
[ARC311Ex] Many Illumination Plans
剖,然后对于轻儿子的贡献每次传入一个数组,然后 dp,复杂度是 \(T(n)=3T(\frac n 2)+O(m)=O(n^{\log_2 3}m)\)。
[ARC096D] Sweet Alchemy
似乎是经典的留 \(n\) 个 dp,然后剩下的直接贪心。
[ARC111E] Simple Math 3
首先不存在,则满足 \((C-B)i<D\),然后如果对于一个 \(i\) 存在,那么只存在 \(1\) 个解,求个和可以计算出有解的方案数,然后减去即可。
[ARC121E] Directed Tree
转逆排列,然后是傻逼容斥
[ABC249Ex] Dye Color
停时题,似乎推狮子有点芬。
[ARC125E] Snack
一眼网络流,转一下最小割,然后是经典选前缀,然后做完了。
[ARC122F] Domination
考虑区间覆盖问题转成图论问题,然后存在 \(k\) 条边就上网络流。
[AGC003E] Sequential operations on Sequence
首先删除 \(a_i>a_{i+1}\) 的 \(i\)。
然后考虑从后往前,维护 \(F_x\) 表示这个序列出现的次数,然后找到最后一个小于等于当前长度的,然后直接打标记,剩下 \(\bmod\) 的部分递归,然后递归到 \(\le n\) 的时候,就可以直接打差分标记,复杂度 \(O(n\log n\log V)\)。
[ARC130F] Replace by Average
似乎直接维护单调栈。
[ARC043F] Jewelry Box
写出代价形式,发现是费用流转线性规划对偶后的式子,所以我们转回来,然后跑原始对偶费用流。
[AGC032E] Modulo Pairing
一个结论是对于 \(a_i+a_j<M\) 用蓝色线,\(a_i+a_j\ge M\),用红色线,则最后匹配形如这个样子:
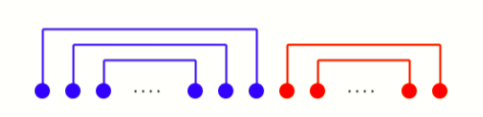
证明可以贪心,往左可能右边不合法,往右可能左边答案太大,然后我们就可以二分分界线。
[AGC067B] Modifications
我们考虑计算 \(f_{l,r}\) 为区间能被删空的方案数,然后我们考虑用 \(C^{r-l+1}\) 减去不能全部删掉的部分,然后可以直接区间 dp。
[AGC045D] Lamps and Buttons
似乎就是令第一个自环在 \(t\),则 \(A+1\sim n\) 每个数所在环内都有一个数 \(<t\)。
枚举 \(t\),然后为了保证 \(t\) 是第一个,然后再容斥一下,剩下的可以直接动态插入计算。
[AGC062D] Walk Around Neighborhood
二分一下,不难知道答案在 \([\frac {a_n}2,a_n]\) 中虽然很显然这个可以二分,但是我们发现,如果从小到大枚举答案 \(d\),那么一个好处是我们一定可以在某一步走到边界上。
那么我们分成 \(S,T\) 两个集合,使得这两个集合最后都恰好走到边长为 \(2d\) 的长方形的边上,然后我们考虑条件是啥,如果都小于等于 \(d\),那么我们需要这些的长度和 \(\ge d\),如果有一个 \(x>d\),那么剩下的需要 \(\ge x-d\), 然后就是简单的了。
[AGC016F] Games on DAG
[ARC117E] Zero-Sum Ranges 2
连续段 dp,然后随便计数一下。
CF468D Tree
重心为根,然后随便搞一下。
CF891D Sloth
树形 dp,设 \(f_{x,0/1,0/1}\) 表示 \(x\) 子树内,\(x\) 是否匹配,子树内部有多少个点未匹配的方案数,然后换根 dp。
CF852H Bob and stages
按斜率排序,上下凸包分开,然后没有点在其中,把叉积拆开,变成 \(3\) 次集合的交,bitset 可以快速 check。
CF776G Sherlock and the Encrypted Data
枚举 \(\sum\) 的数位的最大值,然后数位 dp。
CF578F Mirror Box
黑白染色,观察,发现形如黑色或白色为生成树,然后发现一个成为生成树了另外一个就不行了,所以分开跑 Matrix Tree 定理即可。
CF377E Cookie Clicker
随便维护一下凸包
CF814E An unavoidable detour for home
按层 dp,那么每层的只有一个点和上面的点相连,然后剩下都是内部连和连向下一层的,然后考虑内部连的时候,不能出现重边和自环,容斥一下,最后对于 dp 方程逐步转移即可。
\(O(n^3)\)
CF840E In a Trap
每 \(2^8\) 分一个块,预处理 \(x\) 向上 \(256\) 个点的信息,则每次查询时最后 \(8\) 位相同,考虑前 \(8\) 位即可,然后这个可以预处理前 \(8\) 位增加了多少,然后查询是简单的
CF1896H2 Cyclic Hamming (Hard Version)
CF1801G A task for substrings
考虑找到最后设 \(id_x\) 表示 \(T[1,x]\) 匹配到的最大后缀的单词编号,询问时找到最大的 \(x\) 满足 \(x-|s_{id_x}|+1\le l\),这样发现后面的 \(x+1\sim r\) 都是以这个点结尾的单词数量,可以 \(O(n)\) 预处理,然后 \(l\sim x\) 发现是 \(id_x\) 长度为 \(x-l+1\) 的后缀中出现了多少个单词,这个可以反串建 AC 自动机预处理,最后复杂度是 \(O(\sum|s|+|t|+m\log |t|)\),当然,二分应该可以使用基数排序+线性并查集代替,做到线性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号