dp

动态 dp

P9192 [USACO23OPEN] Pareidolia P

我们设 \(f_i\) 表示目前匹配到了 bessie 的哪一位，同时记录一个 ans，然后我们每一位实际上都相当于我们做了一个线性变换，这个系数显然可以合并，ddp 即可。

CF1286D LCC

首先我们不难知道碰撞时间只有相邻的 \(O(n)\) 种，我们找出这 \(O(n)\) 种，然后转化成 \(\sum_{i=0}[T> i]\)，然后问题变成在这 \(O(n)\) 种时间下还未碰撞的概率，我们从小到大扫描线，每次让我们的限制时间增大，此时我们发现我们比起之前的限制，只多限制了一对相邻的 \(i,i+1\) 不能同时满足 \(i\) 朝向 \(A\) 的同时，\(i+1\) 朝向 \(B\)。

然后我们就可以记录 \(f_{l,r,0/1,0/1}\) 表示考虑了 \([l,r]\) 区间，左/右端点朝左/右，ddp 即可。

OJ7_1024 玩游戏

基本上是一样的，我们考虑我们把大于 \(k\) 的看成 \(1\)，小于的看成 \(-1\)，等于的看成 \(0\)。

首先判断是否有解，如果存在一个长度为 \(3\) 的区间权值为 \(0\) 或者两个 \(0\) 相邻就有解，这个可以直接枚举每一个位置上的 \(k\) 判断。

然后知道有解之后我们一次操作至少可以使一个非 \(k\) 的数变成 \(k\)，此时操作数为 \(n-cnt_k\)，我们考虑能否更加优秀。

首先对于 \(0,0,1,-1\) 的情况，不难发现我们此时可以直接选择 \([0,1,-1]\) 的区间，此时一次可以鲨两个，我们就减少了一次代价。

所以我们大胆猜测可以把相邻的 \([1,-1]\) 匹配，此时减少一次，然后我们 ddp 即可。

写完发现过不去，你发现 \([-1,0,1]\) 的情况一次也可以删两个，不难发现此时相当于不考虑 \(k\)，所以我们 ddp 的时候按 \(k\) 的位置分开 ddp 然后合并即可，

OJ7_1127 希望有羽毛和翅膀

我们枚举 A 选择的编号最大值，为了不算重，这个编号必须选，然后 B 只能选择大于这个编号的。

然后我们有个选择的按评分必须交替的限制，比较麻烦，我们按这一维排序，然后在枚举一个必须选的评分时就可以直接 dp 了，\(f_{0,1}\) 表示上一个是 A/B 选择的，然后直接 dp 即可。

不难发现我们如果对编号扫描线，则一次只有 \(O(1)\) 个位置的决策发生变化，ddp 即可。

神秘 dp

CF995F Cowmpany Cowmpensation

首先我们考虑一个暴力 dp，设 \(f_{x,i}\) 表示考虑完 \(x\) 所在子树后，\(x\) 工资为 \(i\) 的方案数，则我们知道合并一个 \(v\) 上来的时候变化为：

\[f_{x,i}=f_{x,i}\sum_{j=1}f_{v,j} \]

设 \(g_{x,i}=\sum_{j=1}^if_{x,j}\)，则：

\[f_{x,i}=\prod_{v\in son(x)}g_{v,i} \]

然后我们可以知道 \(g_{x,j}\) 是一个关于 \(j\) 的 \(sz_x\) 次多项式，考虑归纳：

• 对于叶子，\(g_{x,i}=i\)，是一个 \(1\) 次多项式。

• 对于非叶子，\(f_{x,i}\) 是儿子的乘积，所以是一个 \(sz_x-1\) 次多项式，然后 \(g\) 是 \(f\) 前缀和，所以是一个 \(sz_x\) 次多项式。

然后我们找 \(n+1\) 个点值代入，然后插值即可。

P8290 [省选联考 2022] 填树

首先考虑我们操作的实质：找到一条链，赋每个点的权值为一个 \(l_i\le x\le r_i\) 的 \(x\)。

我们考虑一个 \(O(nV)\) 的做法。

枚举最小值 \(v\)，且钦定必须取到这个值，则此时值域区间是 \([v,v+K]\)，由于必须取到这个限制很邪恶，差分掉，变成值域区间为 \([v+1,v+K]\)，那么我们就需要在值域在这一部分中计数方案数和权值和。

考虑 dp，对于每一条链，在 lca 处统计贡献。

设 \(f_x,val_x\) 表示以 \(x\) 作为链的一端的方案数，所有方案权值和，然后记录 ans1,ans2 表示全局方案数，权值和。

假设我们在考虑点 \(x\)，能选的值域是 \([l,r]\) 且 \(l\le r\),(\(l>r\) 是简单的)。合并一个儿子 \(v\) 上来的时候：

\[\begin{aligned} ans1&\gets ans1+f_xf_v\\ ans2&\gets ans2+f_xval_v+f_vval_x\\ f_x&\gets f_x+f_v(r-l+1)\\ val_x&\gets val_x+val_v(r-l+1)+f_v(\sum_{i=l}^r i) \end{aligned} \]

此时我们就能做到 \(O(n)\) 一次 dp，复杂度 \(O(nV)\)。

我们考虑这个东西有没有什么性质，我们按 \(l,r,l-k,r-k\) 分成若干段，观察到在每个点的取值 \(l,r\) 都呈现每次 \(v\) 更改时只改变不超过 \(1\) 且变化规律相同的性质，所以所以此时可以得出这个 \((r-l+1)\) 是一个关于 \(v\) 的一次函数，而叶子节点的 \(f,val\) 分别是一个 \(1,2\) 次函数，所以可以归纳得到 \(f,val\) 是一个 \(sz(x),sz(x)+1\) 次函数，要对前缀和插值，所以次数加 \(1\)，找到 \(n+3\) 个点值插值即可。

P5469 [NOI2019] 机器人

首先由于都不能移动到更高的位置，所以最高的高度中最右边的位置是关键的，因为它使得两段独立。

我们考虑区间 dp，设 \(f_{l,r,x}\) 表示考虑区间 \([l,r]\) 最大值不超过 \(x\) 的方案数，则此时我们枚举最大值位置 \(i\)，及其权值 \(k\)，则我们必须满足 \(abs((i-l+1)-(r-i+1))\le 2\)，即 \(l+r-2\le 2i\le l+r+2\)，此时不难发现 \(i\) 取值只有 \(O(1)\) 个，然后甚至可以知道，有用的 \([l,r]\) 状态也不会很多，搜出来只有 \(m=2500\) 个左右。

然后我们枚举最大位置及其权值转移即可，前缀和优化后复杂度 \(O(mV)\)，可以获得 \(50pts\)。

同样考虑按 \(a_i,b_i+1\) 分段，则每一段内部可以归纳得是一个 \(r-l+1\) 次多项式，所以直接 dp 完插值即可。

实际上上面的有些题，除了插值之外，我们其实是可以直接维护多项式的，大家可以自己想想。

P3643 [APIO2016] 划艇

这个东西不知道为啥被分到了插值里面，但是可以引出另外一个套路。

首先我们考虑暴力 dp，设 \(f_{x,i}\) 为考虑前 \(x\) 所学校，第 \(x\) 所学校一定派出，且派了 \(i\) 个的方案数，二维前缀和可以做到 \(O(nV)\)。

我们观察到虽然 \(i\) 值域很大，但是实际上只有 \(O(n)\) 个本质不同的段。

我们首先考虑把这 \(O(n)\) 个段离散化出来，然后改一下 dp 状态，设 \(f_{x,i}\) 表示考虑前 \(x\) 个学校，第 \(x\) 个学校派出的数量在第 \(i\) 段的方案数。

然后此时我们发现，如果前一个学校派出的也在第 \(i\) 段，我们便不好比较大小，所以我们考虑枚举第一个小于第 \(i\) 段的学校在哪里。

则我们的转移变成了

\[f_{x,i}=\sum_{j<x}\sum_{k<i}f_{j,k}calc(cnt_{i,x}-cnt_{i,j},len_i) \]

\(cnt_{i,j}\) 表示 \(1\sim j\) 中有多少个数包含了第 \(i\) 个区间。

然后我们考虑计算 \(calc(x,L)\)，首先我们枚举有多少个学校选择派出，然后计算方案数：

\[\sum_{i=1}^x\binom {x-1}{i-1}\binom L i=\binom {L+x-1}x \]

然后我们转移时枚举 \(j\)，而 \(k\) 的限制可以前缀和解决，预处理组合数，复杂度 \(O(n^3)\)。

CF1295F 和这个题几乎相同，不想写了。

CF303E Random Ranking

我们先离散化出 \(O(n)\) 个段，然后对于每个人，枚举他在哪个段，然后计算这个段有 \(A\) 人，小于这个段的有 \(B\) 人的概率，则这人在 \(B+1,B+2\ldots B+A\) 的概率分别是 dp 出来的概率的 \(\frac 1A\)，暴力计算是 \(O(n^5)\) 的，然后观察 dp 过程是一个类似背包的过程，可以直接分治优化，\(O(n^4\log n)\)，可以通过。

AT_arc113_f Social Distance

首先我们考虑 \(f(x)\) 表示 \(\ge x\) 的概率，则期望就是 \(\int_{0}^{+\infty} f(x)\)。

然后我们考虑对于一个 \(w\) 如何求概率，我们令 \(a_i\gets a_i-w\times i\)，则我们合法条件就是 \(a_i\) 递增。

所以我们直接把每个点的取值区间变成 \([x_{i-1}-iw,x_i-iw]\)，然后此时我们还是把这些区间拆成若干个值域段，那么我们考虑如果一个段内有 \(j\) 个数，那么有 \(\frac 1 {j!}\) 的概率符合条件，然后我们就可以 dp 了，设 \(f_{i,j,k}\) 表示考虑到第 \(i\) 个数，在第 \(j\) 个段，此时这个段有 \(k\) 个人的方案数，然后转移需要乘上一个 \(i\) 在当前段的概率，然后再考虑是否新开了一段，乘上 \(\frac 1 k\)。

这个东西我们发现，如果我们端点的相对位置不发生改变的话，那么我们每一段的左右端点都形如 \(A-Bw\) 和 \(C-Dw\) 的形式，此时再当前段的概率就是一个关于 \(w\) 的一次多项式，所以最后是一个关系 \(w\) 的 \(n\) 次多项式。

先 \(O(n^2)\) 找到端点发现相对位置移动的断点，然后 dp 时暴力维护多项式，最后积分计算对于答案的贡献即可。

中间新开一段的部分使用前缀和优化，\(O(n^6)\)。

dp 套 dp

这里面套的可能是 dp 或者栈啊之类的东西，但是你似乎都可以看成一个自动机。

然后自动机可以使用 Hopcroft 最小化。

大概是你不断把节点划分成若干等价类，一旦一个等价类中的点同一个转移函数指向了不同等价类就直接启发式分裂。

P10614 BZOJ3864 Hero meet devil

dp 套 dp 板子题。

我们首先考虑最长公共子序列如何计算。

\[f_{i,j}=\max(f_{i-1,j},f_{i,j-1},f_{i-1,j-1}+[S_i=T_j]) \]

然后我们考虑如果我们只知道 \(S\) 怎么办，不难发现我们可以把 \(j\) 从 \(1\) 到 \(m\) 计算，然后每轮中计算 \(i\)。

我们先交换一下 \(i\) 和 \(j\)(虽然 dp 方程没有变就是了)。

我们先观察一下 \(F=f_j\) 有什么性质，递增，且相邻两项之差 \(\le 1\)，所以我们可以知道 \(F\) 实际上只有 \(O(2^n)\) 种！。

所以如果我们知道 \(F\) 在 \(T_i=c\) 时的变化，我们就可以快速地得到 \(F\) 转移后的状态 \(F'\)，然后就可以 dp 了！

然后我们考虑 \(F=f_j\) 的变化。

\[F'_i=\max(F_i,F'_{i-1},F_{i-1}+[S_i=T_i]) \]

不难发现我们可以预处理自动机转移，然后直接 dp 即可，复杂度为 \(O(2^nm|\sum|)\)。

OJ7_1035 橘子

首先我们考虑我们 \(1\) 号节点是怎么打的，不难发现是分别打了一个长度为 \(2^0,2^1,2^2,2^{n-1}\) 的区间的最大值。

所以我们必须满足这些区间最大值在这 \(m\) 个数内部，然后由于有一个最长上升子序列的限制，所以我们把这 \(m\) 个数从小到大考虑。

然后我们一个想法是吧最长上升子序列压进状态，由于上一个题的启发，我们知道同样可以差分后状压维护。

然后我们维护 \(f_{i,S,T}\) 表示此时我们放在了 \(S\) 这些区间内部，最长上升子序列状态为 \(T\) 的方案数，然后每次考虑放到哪个区间，然后方案数是一个简单组合数。

然后直接 dp 即可，看起来复杂度是 \(O(mn4^n)\)，但是不难知道 \(T\) 是 \(S\) 的子集，所以实际复杂度是 \(O(mn3^n)\) 的，比联考的唐氏 sol 不知道高到哪里去了。

OJ7_1008 树上基础问题

首先我们需要知道怎样的一棵树是满足条件的：

对于任意两个权值相同的节点，中间的路径上一定存在一个节点权值小于他们。

然后我们考虑状压子树内部形成的权值的单调栈，大于的当前权值的部分可以直接放进初值里面，然后转移是一个若干个子集卷积。

直接暴力卷积+剪枝，复杂度为

\[O(n(3^k+3^{k-1}+3^{k-2}+\ldots))=O(n3^k) \]

CF1299D Around the World

首先看到异或，不难想到线性基。

然后我们发现值域很小，暴搜一下不同的线性基的个数，发现只有 \(c=374\) 个，这个东西看起来在理解范围内。

然后我们考虑由于我们只能断开 \(1\) 相邻的边，则我们删掉 \(1\) 后，形成的每个连通块内部的边是不受影响的。

由于我们需要从 \(1\) 开始，到 \(1\) 结束，所以我们只需要关注每个连通块的环即可。

我们对于所有连通块 \(i\)，把连通块内所有环形成的线性基 \(b_i\) 求出来。

设 \(f_{i,x}\) 为考虑前 \(i\) 个连通块，目前线性基状态为 \(x\) 的方案数。

如果这个连通块内部已经线性相关，说明必须断开 \(1\) 到这个连通块内部的边。

否则我们考虑 \(1\) 和这个连通块有几条边：

• 一条边，可以断可以不断，\(f_{i,x}\) 贡献到 \(f_{i+1,x}\) 和 \(f_{i+1,x\cup b_i}\)

• 两条边，都断是 \(f_{i,x}\to f_{i+1,x}\)，断一个是 \(2f_{i,x}\to f_{i+1,x\cup b_i}\)，否则我们还有一个 \(1\) 和剩下可能的三元环权值 \(w\)，\(f_{i,x}\to f_{i+1,x\cup b_i\cup w}\)。

然后预处理转移后直接 dp 即可，复杂度 \(O(cn)\)

CF924F Minimal Subset Difference

首先我们考虑对于一个数怎么计算答案。

不难知道我们背包计算可达性即可，设 \(f_i=0/1\) 表示能不能是 \(i\)，转移就是 \(f_i\to f_{i+c},f_{|i-c|}\)。

我们考虑加入一些剪枝，首先我们知道答案肯定不超过 \(9\),所以 \(f\) 大于 \(90\) 的部分就没用了,因为 \(90\) 至少用了 \(10\) 位,剩下最多 \(9\) 位,而 \(90-(9\times 9)\ge 9\),所以是没用的.

然后此时我们的复杂度一个跟 \(2^{90}\) 有关的式子，爆！

不难猜测有很多状态无用，用个 __int128 记录 f，然后暴搜状态，发现只有不到 \(2\times 10^4\) 个。

然后我们可以对于每个状态预处理转移。

然后对于计算答案，直接数位 dp 的时候记录一下在自动机上哪个状态即可。

由于询问只有 \(k\)，我们数位 dp 的时候多记录 \(k\) 一维即可。

P8497 [NOI2022] 移除石子

首先考虑对于一个确定的 \(a\) 如何计算答案，首先我们发现这个恰好 \(K\) 枚太邪恶了，考虑想办法变成变成小于等于 \(K\)，打表之后发现只有两种情况不合法：

• \(n=3,K=a_1=a_2=a_3=1\)
• \(K=1,\sum a_i=0\)。

特判一下这两种即可。

然后我们考虑对于 \(a\) 如何计算其最小 \(K\)。

首先找点性质，首先区间长度 \(\le 5\)，且不会存在两个相同的 \(2\) 操作。

然后我们设计 dp，设 \(f_{i,j,k}\) 表示考虑 \(<i\) 的位置，有 \(j\) 个位置至少延伸到 \(i\)，\(k\) 个至少延伸到 \(i+1\)，最少的 \(K\)。

枚举有 \(l\) 个区间从这一位出发，有多少区间在这一位结束，转移即可。

此时我们的复杂度变成了 \(O(\prod(r_i-l_i+1) n)\),可以得到 \(40pts\)。

然后考虑如何更好，我们可以不断尝试减少 \(j,k\) 的上界，然后和此时的代码对拍，

然后可以知道 \(j,k,l\le 2\) 也可以满足条件。

然后我们发现我们 \(f_i\) 只有 \(9\) 个状态，且根据猜测，\(9\) 个状态的答案不会差距太大，所以状态是显然跑不满 \(O(K^9)\) 的。

所以我们暴搜状态，发现只有 \(10^4\) 种不到，然后预处理转移，根据转移代价，不难发现本质不同的转移只有 \(8\) 种。

然后一个一个数 dp ，dp 时直接考虑 \(8\) 种转移的系数，转移即可。

树上依赖性背包

首先需要会 dfn 序背包

P6326 Shopping

第一种方法是由于需要是一个连通块，然后 dp 复杂度跟连通块大小有关。

我们可以直接点分治+dfn 序背包即可。

还有一种很舒服的方案是 dsu on tree，然后做 dfn 序背包，但是具体还没想好，笋的课件声称这种可以求出每个子树的答案。

P3780 [SDOI2017] 苹果树

我们不难发现我们就是选择一条链免费选一次，然后剩下的做依赖性背包，这个我们可以 dfn 序前缀做一遍，后缀做一遍，然后合并即可。

HDU6566 The Hanged Man

首先可以直接 dp 背包 \(O(nm^2)\)，显然无法通过。

我们考虑按 dfs 序加点，但是我们加入一个点的时候可能从一个子树跑到另外一个子树去了，就是如下情况。

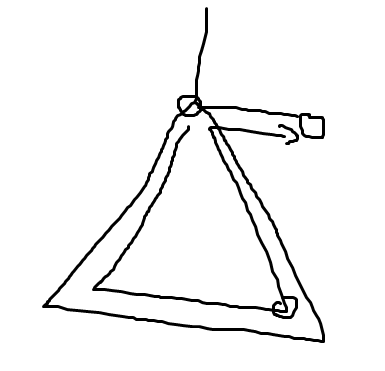
此时我们需要知道这个新的点的父亲是否被选择才能决定这个点的选择情况，不难发现这个点是之前一个点的祖先，所以我们直接状压所有祖先是否被选择过然后背包即可做到 \(O(m\sum 2^d)\) 了，真是叮叮又咚咚啊。

我们考虑如何优化，上一个树剖，然后先遍历轻儿子，这样我们跳跃的时候，是直接跳到这条链顶的父亲的其他儿子，所以我们只需要状压每个重链的父亲即可，这样复杂度变成了 \(O(m\sum 2^{e})\)，\(e\) 表示每个点到根的轻链个数，伟大的笋先生证明了这样的复杂度是 \(O(n^{\log_2 3}m)\) 的，随便通过。

容斥

OJ7_10018 小D与随机

给一颗有根树，根节点为 \(1\) 和常数 \(k\)，你要对点重新标号（原来的 \(i\) 号点标 \(w\_i\)，其中 \(w\) 构成一个排列，重标号后根不改变），定义点 \(i\) 是好点当且仅当这个点的权值是当前点到根上的链上所有节点的权值的最大值。

而对于一次重新标号， 我们称这颗树的权值是 \(k\) 的 （好点个数 \(c\) ）次方。

现在你要求出所有可能出现的重标号的树的权值的和。

（两个重标号方案不同当且仅当 \(w\) 不同）

前置知识：树的拓扑序计数。

给定一张 \(n\) 个点以 \(r\) 为根的叶向森林，拓扑序的方案数是：\(\frac {n!}{\prod siz_i}\)。

我们先计算期望，再乘上 \(n!\)。

我们考虑如果我们确定的黑点集合，那么我们要满足什么条件：

• 对于一个黑点，要大于第一个黑点祖先。
• 对于一个白点，要小于第一个黑点祖先。

然后如果把从大到小连边，忽略边的方向，则我们得到了一颗新的树。

由于这个边的方向很邪恶，有上有下，我们考虑容斥一部分，我们容斥掉向下的边，则我们白到黑的边只剩下了 向上，此时有 \(-1\) 倍的贡献，或者任意上下，此时相当于此子树独立出去了。

此时我们其实相当于一个外向树森林，然后我们可以对这个东西做拓扑序计数的，要乘上的有我们每个黑点的权值 \(k\)，还有从向下变成向上带来的贡献 \((-1)^E\)。

首先如果 \(i\) 不是 \(1\)，则 \(i\) 一定有一个黑色祖先。

我们考虑 dp 来计算这些乱七八糟的东西，设 \(f_{i,j}\) 表示 \(i\) 子树，这个黑色祖先所在的外向树大小为 \(j\) 的各种玩意之和（子树大小除去这个虚拟点本身），则考虑转移：

先考虑子节点之间的合并，发现直接相乘就好了，然后再考虑 \(i\) 带来的影响。

• \(i\) 是黑色点，此时不难知道是 \(f'_{i,j+1}\gets k\times {j+1}\times f_{i,j}\)，即表示 \(i\) 加入该外向树。

• \(i\) 是白点，分成两种情况。

  • 容斥为向上，则此时祖先的外向树大小 \(+1\) 了，且由于多了一条边，存在一个 \(-1\) 的贡献，则 \(f'_{i,j+1}\gets -f_{i,j}\)。
  • 否则因为无所谓，等价于不考虑这个白点，\(f_{i,j}\gets f_{i,j}\)。

复杂度等价于树形背包，\(O(n^2)\)。

同样的对边容斥套路还有 AT_agc058_f，但是那个题还有非常神秘的转化。

P4547 [THUWC2017] 随机二分图

由于期望的独立性，我们可以对于每组完美匹配出现的概率求和即可。

先考虑如果只有第 \(0\) 类边怎么做。

我们直接 dp，设 \(f_{i,S}\) 表示考虑到左边第 \(i\) 个点，右边还剩下 \(S\) 集合内的点的期望，然后每次只需要枚举匹配点并考虑这个点匹配概率。

然后考虑有 \(1,2\) 类边的情况，由于匹配顺序可能比较混乱，所以我们考虑改成 \(f_{S,T}\) 表示左边剩下 \(S\)，右边剩下 \(T\) 的期望。

然后为了不算重，我们考虑每次必须包含 \(S\) 中编号最小的节点。

看起来对了吗？似乎并不是。

如果存在 \(1\) 类边 \((A,B),(C,D)\)，\(0\) 类边 \((A,B),(C,D)\)，那么如果我们选择了 \(1\) 类边中的 \((A,B)\) 后就不能选择 \(0\) 类边的 \((C,D)\)，否则就会出现一些神秘的重复。

我们考虑把 \(1\) 类边直接拆成两条边 \((A,B),(C,D)\) 且概率都是 \(\frac 1 2\)，则此时我们发现可以一次如果我们该 \(1\) 类边的出现概率变成了 \(\frac 1 4\)，所以我们增加一条同时选择 \((A,B),(C,D)\) 的边，概率为 \(\frac 1 4\) 即可，而 \(2\) 类边不难发现概率为 \(-\frac 1 4\) 即可。

看起来状态数最多是 \(\sum_{i=0}^n\binom n i^2=\binom {2n}n\)，实际上由于有 \(4n\) 个点一定包含左侧前 \(n\) 个点，所以状态数没有这么大。

然后直接 dp 即可。

OJ7_10019 狂战斧2048型

考虑如果是恰好 \(i\) 个人不好计算，考虑设置一个容斥系数满足只要存在 \(c_i\) 个人就有 \(c_i\) 的贡献就非常好。

不难知道需要满足：

\[a_i=\sum_{j=0}^ic_j\binom i j \]

看一眼，这个可以二项式反演，NTT 优化卷积即可得到 \(c_i\)，得到 \(c_i\) 之后的部分是好计算的。

AT_abc236_h Distinct Multiples

这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！这是什么，看一眼！

魔怔。

集合划分容斥，具体可以去这篇博客，讲的很好，这里不展开。

首先我们如果存在 \(a_i=a_j\)，就让 \(i,j\) 连边，然后我们需要每个点都单独形成一个连通块的方案数计数。

让我们考虑一下如何设计这个容斥系数。

不难知道对于每个连通块独立，所以我们只需要考虑设计一个连通块的容斥系数即可。

由于一个连通块内部是完全图，所以我们只需要用连通块大小来区分，我们不妨设 \(f_i\) 表示大小为 \(i\) 的连通块的贡献系数，首先我们知道没有连通限制的时候我们的系数是 \(g_i=[i=1\ \text{or}\ i=0]\)，则我们得到：

\[\exp F=x+1 \]

对他做 \(\ln\) 得到 \(f_i=(-1)^{i-1}(i-1)!\)，实际上这个系数也可以 dp 得到。

然后我们既然已经计算好了容斥系数，剩下就不用考虑不等限制了，枚举钦定的连通块集合 \(S\)，然后直接做集合幂级数 exp 即可，\(O(n^22^n)\)，直接枚举子集转移也可以通过。

这个题由于是完全图，所以我们可以用集合大小来推导容斥系数，否则实际上我们可以枚举集合来推导容斥系数。

AT_abc306_h Balance Scale

首先假设 = 不存在的情况，问题变成对于每一条边定向，然后形成一个 DAG。

然后我们考虑怎么 dp 一下这种东西，枚举入度为 \(0\) 的点集删掉，然后计算下面的部分，然后你发现算重了，比如入度为 \(0\) 的点为 A,B。

那么你都干了什么呢，枚举 A 作为入度为 0 的点，然后下一层又选了 B，还有选了 B 再选 A，以及同时选 A,B。

此时你发现了什么呢，你每个子集都会计算一次，显然爆炸，我们考虑设计大小为 \(i\) 的点集的容斥系数 \(f_i\)。

必须满足

\[\sum_{i=1}^n\binom n if_i=1 \]

不难构造出 \(f_i=(-1)^{i+1}\)，完全胜利。

然后考虑存在等于怎么办，我们发现等价于这两个点是同时考虑的，那么我们的容斥系数变成了 \((-1)^{cnt+1}\)，其中 \(cnt\) 是连通块数，然后 dp 即可。

P10221 [省选联考 2024] 重塑时光

我们转化一下题意：

重排后切 \(k\) 次，等价于分成 \(k+1\) 个点集，每个点集内部是 DAG，然后 \(k+1\) 个大点也形成了 DAG。

考虑计数方案数，然后除以总方案数。

然后我们先考虑外层大点的 DAG 容斥，由于上面的部分，设 \(f_{S,i}\) 表示划分了点集 \(S\) ，分成 \(i\) 个大点的方案数，然后枚举入度为 \(0\) 的点集 \(T\) ，分成 \(j\) 个大点，转移。

预处理个 \(g_{S,i}\) 表示 \(S\) 分成 \(i\) 个互不相连的大点的方案数，\(h_S\) 表示 \(S\) 集合划分成一个大点的方案数。

\[f_{S,i}=\sum chk(T,S/T)\sum_{j=1}^if_{S/T,i-j}g_{T,j}(-1)^{j+1}\\ g_{S,i}=\sum chk(T,S/T)chk(S/T,T)g_{S/T,i-1}h_T\\ h_S=\sum_{u\in S}chk(S/u,u)h_{S/u} \]

\(chk(A,B)\) 表示是否不存在 \(B\to A\) 的边。

然后这样复杂度是 \(O(3^nn^2)\) 的，卡常后可以通过。

但是我们发现这个东西长得很像卷积，归纳可以知道 \(f_S\) 是一个 \(n\) 次多项式，找 \(n\) 个值出来，插值出多项式即可得到 \(f_{2^n-1}\)。

好，现在我们已经得到了我们最后的多项式，考虑如何从 \(f_{x,i}\) 统计答案。

我们先选择这 \(i\) 个位置，然后重排这 \(i\) 段，最后切割顺序还有一个 \(k!\)，所以方案数是：

\[i!k!\binom {k+1}i \]

然后总方案数是选择切割位置，切割顺序，排列顺序，就是：

\[\binom {n+k}kk!n!=(n+k)! \]

除以这个东西即可。

组合意义

CF1842G Tenzing and Random Operations

首先你想直接拆贡献，发现飞天了，很邪恶。

结果一看，怎么 uob 又做出来了，然后他神奇的表达你又听不懂，看过程看到天地灭都看不懂，很难过。

打开题解一看，组合意义保平安。

先计算方案数，我们考虑 \(\prod a_i\) 组合意义，表示在 \(i\) 处有 \(a_i\) 个球，然后你每个位置选一个球的方案数。

然后我们考虑这个 \(+v\) 有啥用，相当于给了后缀每个位置 \(v\) 个球。

我们发现我们实际用到的操作数量不超过 \(n\)，考虑从这一部分来计算，剩下没用过的不做区分，可以任意放。

所以我们设 \(f_{i,j}\) 表示考虑到 \(i\)，用了 \(j\) 次操作的方案数，考虑如何 dp 转移。

• 使用 \(a_i\)，\(a_if_{i,j}\to f_{i+1,j}\)。
• 使用一个考虑过的操作 \(j\)，\(f_{i,j}\times jv\to f_{i+1,j}\)
• 用一个新的，考虑这个属于哪次操作，\(f_{i,j}(m-j)\to f_{i+1,j+1}\)。

然后答案就是：

\[\frac {\sum f_{n+1,i}n^{m-i}}{n^m} \]

AT_arc124_e Pass to Next

我们首先考虑怎么才能使得 \(S\) 两两不同，我们发现如果所有 \(a_i\ge 1\)，那么我们可以让 \(a_i\) 全部减去 \(1\)，然后此时 \(S\) 不变。

所以我们只需要按所有 \(a_i\ge 0\) 做一遍，减去 \(a_i\ge 1\) 的部分即可。

然后我们考虑怎么计数这个，首先假设是一条链，考虑 \(\prod a_i\) 的组合意义。

那么我们第 \(i\) 个人就有两种决策：

• 选择自己本来剩下的。
• 选择 \(i-1\) 传给他的。

首先我们定义 \(S1(n)=\sum_{i=0}^n i,S2(n)=\sum_{i=0}^n i^2\)。

我们考虑直接 dp，由于自己剩下的跟传给下一个人有关，传过来的和上一个人有关，那么我们考虑把这两种分开。

设 \(f_{i,0}\) 表示选原来就有的，因为有可能下一个人选择 \(i\) 传过去的，所以这一位的贡献系数不容易确定，和下一位一起确定，那么我们 \(f_{i,0}\) 表示的是前 \(i-1\) 个人的方案数。

而 \(f_{i,1}\) 表示我传多少给下一个人都不会改变这一位的贡献系数，所以表示前 \(i\) 个人的方案数。

考虑转移：

\[\begin{aligned} f_{i+1,0}&\gets f_{i,0}\times S1(a_i)\\ f_{i+1,0}&\gets f_{i,1}(a_i+1)\\ f_{i+1,1}&\gets f_{i,0}\times (\sum_{x=1}x(a_i-x))\\ f_{i+1,1}&\gets f_{i,1}\times S1(a_i) \end{aligned} \]

然后我们考虑如何初始化，首先我们钦定 \(1\) 号点选还是不选，初始化是直接初始化为 \(f_{1,c}=1\)，就相当于只有这种方案有贡献，然后转移回 \(1\) 号点，得到答案 \(f_{1,c}\)，但是一开始初始化时 \(f_{1,c}=1\)，需要减去，即返回 \(f_{1,c}-1\) 即可。

「LibreOJ β Round #7」匹配字符串

首先我们考虑设 \(f_i\) 表示上一个 \(0\) 在 \(i\) 处放的方案数。

则我们知道 \(f_i=\sum_{i-m\le j\le i-1} f_j\)，前缀和一下得到：

\[s_{i}-s_{i-1}=s_{i-1}-s_{i-m-1}\\ s_i=2s_{i-1}-s_{i-m-1} \]

\(s_0=1\).

首先发现这是一个线性递推，可以 bostan-mori 在不用 FFT 情况下做到 \(O(m^2\log n)\)。

考虑 \(m\) 较大怎么做，我们发现我们转移过程可以抽象成一个在一条数轴上走的过程，从 \(i\) 走到 \(i+1\) 系数乘上 \(2\)，走到 \(i+m+1\) 系数乘上 \(-1\)。

枚举第二种转移走了多少步，\(s_n\) 是：

\[\sum_{i=0}(-1)^i2^{n-(m+1)i}\times C(n-(m+1)i+i,i) \]

这个复杂度是 \(O(\frac n m)\) 的，然后拼一下得到了 \(O(n^{\frac 2 3}\log^{\frac 1 3}n)\) 做法，看起来随便过。

带边数的无向连通图计数

给定 \(n\)，对于所有 \(m\) 求满足 \(0\le m\le \binom n 2\) 的 \(n\) 个点 \(m\) 条边的带标号无向连通图个数。
\(1\le n\le 100\)。

首先如果我们的 GF 水平足够高，那么我们可以发现：

\[\exp G=\sum_{n\ge 0}\frac {x^n}{n!}(1+y)^{\binom n 2} \]

然后直接做二元多项式 \(\ln\) 就是 \(O(n^3\log n)\)，但是多项式素质太差了，考虑 dp 做法。

首先我们考虑暴力容斥，记录 \(g\) 表示 \(n\) 个点 \(m\) 条边的无向图个数，然后枚举和 \(1\) 连通的连通块大小及其边数容斥，复杂度 \(O(n^6)\)。

我们考虑换种方法容斥，设一个选了 \(m\) 条边的方案，且形成 \(k\) 个连通块方案块的方案是 \(F_{m,k}\)
现在我们还是 \(m\) 条边，但人为划分出来 \(j\) 个块一定不两两相连，但块内任意连边，方案是 \(G_{m,j}\)。

那么我们知道：

\[G_{m,k}=\sum_{j=k}{j\brace k}F_{m,j}\\ F_{m,k}=\sum_{j=k}(-1)^{j-k}{j\brack k}G_{m,j}\\ F_{m,1}=\sum_{j=1}(-1)^{j-1}(j-1)!G_{m,j} \]

首先你可以发现，这个容斥系数怎么跟上面某个 ABC 题一样呢，这之间有什么关系呢，读者可以自己找找。

然后我们考虑如何计算 \(G\)，再做一次容斥，设 \(H_{i,j,k}\) 表示考虑了 \(i\) 个点，分了 \(j\) 了相互之间一定没有边的块，用 \(k\) 条边可以用的方案数。

则 \(G_{m,j}=\sum_{k\ge m}H_{n,j,k}\binom k m\)。

发现此时：

\[\begin{aligned} F_{m,1}&=\sum_{j=1}(-1)^{j-1}(j-1)!\sum_{k\ge m}H_{n,j,k}\binom k m\\ &=\sum_{k\ge m}\binom k m\sum_{j=1}(-1)^{j-1}(j-1)!H_{n,j,k} \end{aligned} \]

我们发现，这个 \(j\) 很邪恶，但是如果我们能把 \((-1)^{j-1}(j-1)!\) 放进 dp 过程中，就可以做到 \(O(n^4)\)。

首先如果直接 dp，怎么想都要记录一个 \(j\)，不大行，考虑组合意义，除了 \(1\) 所在的连通块剩下的随便排列，且每增加一个连通块多一个 \(-1\) 的贡献，这样我们每种方案就会被算 \((-1)^{j-1}(j-1)!\) 次，全对了。

于是 dp 时第一次加入一个包含 \(1\) 的连通块，后面剩下的每次分配标号即可。

当然，我拿这个题咨询 🍏 有没有见过原题，他告诉我们：

你发现，设 \([x^m]F_n(x)\) 为所求答案，则：

\[\begin{aligned} F_n(x)=(1+x)^{\binom n 2}-\sum_{i=1}^{n-1}\binom {n}{i-1}F_i(x)(1+x)^{\binom {n-i}{2}} \end{aligned} \]

然后直接拉插就是 \(O(n^4)\) 的，完全胜利！！！

OJ7_1066 节日

由于期望线性性，我们发现答案就是

\[\sum_{i=0}[到 i 时刻还没全部点亮] \]

我们特判掉 \(i=0\) 的情况。

我们考虑枚举这个时刻恰好未点亮的集合 \(S\)，概率为 \(f(S)\)，然后我们考虑钦定，然后子集反演，设 \(g(S)\) 为钦定 \(S\) 子集没被点亮的概率，则：

\[\begin{aligned} g(S)&=\sum_{S\subset T}f(T)\\ f(S)&=\sum_{S\subset T}g(T)(-1)^{|T|-|S|} \end{aligned} \]

然后我们需要计算：

\[\begin{aligned} \sum_{S}f(S)&=\sum_{S}\sum_{S\subset T}(-1)^{|T|-|S|}g(T)\\ &=\sum_{T}g(T)(-1)^{|T|+1} \end{aligned} \]

然后我们就需要计算 \(g(T)\)。

我们考虑把原数组按 \(T\) 分成若干极长连续段，则每一个没被选中的长度为 \(l\) 的段在倒数第 \(1,2,\ldots\) 次能选取的方案数分别是 \(l,l-2,l-4,\ldots\)

然后我们就有一个 \(O(np(n))\) 的做法。

枚举没被选中的部分的长度集合，然后由于我们不能有两段相邻，我们可以在每段后面放上一个被钦定的点，然后暴搜拆分数，每次知道集合后，对于答案的贡献就是每次能选取的概率的前缀积的和（即到每个 \(i\) 时刻还未点亮的概率和）。

然后我们需要对于每组拆出来的方案，计算原本有多少种序列满足这个方案。

我们设长度为 \(i\) 的区间有 \(c_i\) 个，则我们先进行排列的方案数是：

\[\frac {(\sum c_i)!}{\prod c_i!} \]

然后我们因为这是一个环，所以考虑第一段是哪段，由于第一段长度为 \(i\) 的概率有 \(\frac {c_i}{\sum c_i}\)，而此时的方案数是 \(i\)，所以总方案数就是：

\[\begin{aligned} &\frac {(\sum c_i)!}{\prod c_i!}\sum_{i=1}\frac{ic_i}{\sum c_i}\\ &=\frac {(\sum c_i)!}{\prod c_i!}\frac n{\sum c_i}\\ &=\frac {n(\sum c_i-1)!}{\prod c_i!} \end{aligned} \]

然后我们考虑如何 dp，我们考虑这个前缀积之和的组合意义，即从某个下标开始就不选择乘积了。

我们设 \(f_{i,j,0/1}\) 表示目前有 \(i\) 段，长度和为 \(j\)，还是否选择乘积的概率之和。

我们从后往前考虑操作。

先我们考虑这次操作，我们能选择的位置还有 \(j-i\) 个（因为每段最后一个位置是钦定点亮的）。

然后我们考虑下次操作，每段区间能选择的位置减少了 \(2\)，然后本来只有 \(1,2\) 个位置能选的区间似了。

我们枚举有 \(x\) 个长度为 \(1\) 的区间， \(y\) 个长度为 \(2\) 的区间，则我们得到转移方程：

\[\begin{aligned} f_{i,j,1}&=\sum_{x,y}(f_{i-x-y,j-2i+x,1}+f_{i-x-y,j-2i+x,0})\frac 1 {x!y!}\frac {j-i}n\\ f_{i,j,0}&=\sum_{x,y}f_{i-x-y,j-2i+x,0}\frac 1 {x!y!} \end{aligned} \]

初值 \(f_{0,0,0}=1\)。

最后 \(f_{i,n,1}\) 的贡献系数是 \(n(i-1)!(-1)^{i+1}\)，上面拆分数部分证明了。

然后我们就可以做到 \(O(n^4)\) 了。

然后我们考虑如何优化到 \(O(n^3)\)，我们发现转移的时候 \(x,y\) 的贡献是可以拆开的，所以我们把转移拆成两步，

• \(f_{i,j}\gets g_{i-x,j-i}\)。
• \(g_{i,j}\gets f_{i-y,j-i}\)。

然后我们观察为啥这是对的，因为我们发现等价于：

\[f_{i,j}\gets g_{i-x,j-i}\gets f_{i-x-y,j-i-(i-x)} \]

然后你发现后面部分就是 \(f_{i-x-y,j-2i+x}\)，全对了。

然后这样就可以做到 \(O(n^3)\)，可以获得 \(92pts\)。

后面我们可以发现一个剪枝，有这样一个不等式：\(j-x\ge 2(i-x)\to x\ge 2i-j\)，加上这个剪枝后即可通过。

延迟钦定

CF1608F MEX counting

经 典 老 番

我们来考虑一下这个问题怎么 dp。

首先考虑设置状态，根据常识，我们应该有两维状态分别是下标和当前的 mex，但是我们发现这两个信息并不能很好的描述当前的局面，因为我们可能出现加入一个数后 mex 变大很多的情况，所以我们应该再加入一维表示有有哪些选过的数大于目前的 mex。

但是直接维护这些数形成的集合复杂度又飞天了，怎么办呢，我们发现，每种大小相同的集合出现次数是相同的！所以我们可以对于每种大小只维护其中一种情况对应的方案即可，然后转移的时候再考虑对于 mex 造成的贡献。

设 \(f_{i,x,c}\) 表示考虑前 \(i\) 个数，当前 mex 为 \(x\)，有 \(c\) 种数 \(>x\) 的方案数，且未钦定这 \(c\) 个数的相对顺序。

首先 mex 不变的方案是简单的，

• 选的数出现过，\(f_{i,x,c}\times (x+c)\to f_{i+1,x,c}\).
• 选的数没出现过，\(f_{i,x,c}\to f_{i+1,x,c+1}\)。

当前是选的数 mex 的时候，由于直接枚举谁转移到了谁是 \(O(k^2)\) 的，总复杂度 \(O(n^2k^2)\)，无法通过。

我们设置一个辅助数组 \(g\) 辅助转移，设 \(g_{x,c}\) 表示 \([0,x-1]\) 都出现过，大于等于 \(x\) 一共有 \(c\) 种不同的数，也未钦定过相对顺序。

首先 \(f_{i,x,c}\to g_{x+1,c}\) 表示选了 mex，然后考虑 \(g\) 内部如何转移，以及 \(g\) 如何转移回 \(f\)。

• \(g_{x,c}\times c\to g_{x+1,c-1}\)，表示出现了一个 \(x+1\).
• \(g_{x,c}\to f_{i+1,x,c}\)，表示转移在这里选不出来 \(x+1\) 了，此时 \(mex=x+1\)。

由于 \(g_{x,c}\) 中 \(x\) 的取值只有 \(L_{i}\sim R_{i+1}\)，然后 \(\sum\) 是 \(O(n)\) 的，所以复杂度 \(O(n^2k)\)。

实际上我们也可以修改 \(f\) 定义，先钦定这 \(c\) 个数的相对顺序，然后 \(g\) 的定义和 \(f,g\) 的转移就有一定变化，读者可以自己试试。

AT_code_festival_2017_qualc_f Three Gluttons

首先我们只考虑 C 选的 n/3 个数，剩下的 \(\frac 2 3n\) 插进去的方案数是 \(\prod_{i=1}^{\frac n 3}(3i-1)(3i-2)\)。

然后我们考虑如何 dp，考虑这个 A,B 选择的位置都是选了一个然后跳跃一段的，这让我们联想到 mex counting。

我们考虑设计 dp 状态为 \(f_{i,p,q}\) 为都选了 \(i\) 个数，A,B 序列分别选到了 \(p,q\) 的方案数，然后枚举下一个选择位置 \(A,B\)，转移到 \(f_{i+1,A,B}\)，但是贡献系数呢？

不妨考虑记录 \(cnt_{p,q}\) 表示 \(A_1,A_2\ldots A_p,B_1,B_2\ldots B_q\) 中不同数的出现次数，则我们发现选择 \(i\) 时 \(c\) 一定要出现某 \(c1=cnt_{p,q}-2i\) 个数，到选择 \(i+1\) 时需要出现某 \(c2=cnt_{A,B}-2(i+1)\) 个数，我们考虑此时如何计算贡献系数。

我们发现，除了这 \(c2\) 个数，剩下的 \(c\) 被钦定的数可以先不管了，我们采用延后钦定的套路，等到需要确定的时候再来处理，此时我们考虑容斥系数，我们发现我们需要在 \(i-c1\) 个数中，确定 \(c2-c1\) 个数，而且可以随便排序，所以转移系数是：

\[\binom {i-c1}{c2-c1}(c2-c1)! \]

然后我们考虑计算最后 \(f_{n/3,p,q}\) 对于答案的贡献，我们剩下 \((\frac n 3-(cnt_{p,q}-\frac 2 3 n))\) 个数还未确定，他们可以任意排列，就是 \((n-cnt_{p,q})!\)，记得乘上剩下 \(\frac 2 3n\) 个数插入的方案。

此时是 \(O(n^5)\)，然后拆开组合数，发现 \(p,q\) 和 \(A,B\) 独立，前缀和优化就是 \(O(n^3)\) 的了。

QOJ9128 Priority Queue 3

放个 eltaos 的博客，真的不想写了/dk

杂题

AT_arc153_d Sum of Sum of Digits

首先不难想到数位 dp，我们设 \(f_{i,j}\) 表示考虑了从小到大前 \(i\) 位，有 \(j\) 个数进位的最小代价，我们把所有数按只考虑前 \(i\) 位的相对大小排序，这样我们进位的一定是前 \(j\) 个数。

然后我们枚举这一位 \(X\) 是多少，以及上一位进位了前 \(j\) 个数，计算此时进位了 \(c\) 个数和这一位产生的贡献都可以在从计算 \(j-1\) 后 \(O(1)\) 得到。

CF1188D Make Equal

我们首先将 \(a\) 排序，然后假设所有数最后都变成了 \(x+a_n(x\ge 0)\)，然后我们就需要 \(\sum \text{popcnt}(x+a_n-a_i)\) 最小，然后令 \(a'_i=a_n-a_i\)，不难发现就是上面那一个题。

AT_abc134_f Permutation Oddness

我们考虑拆贡献，我们在左右两边各放 \(n\) 个点，然后左第 \(i\) 个点向右边的第 \(p_i\) 个点连黑色边。

然后我们在所有的 \(i\) 和 \(i+1\) 之间连红色边，如图所示，则不难知道实际上怪异度就是红黑之间的交点个数。

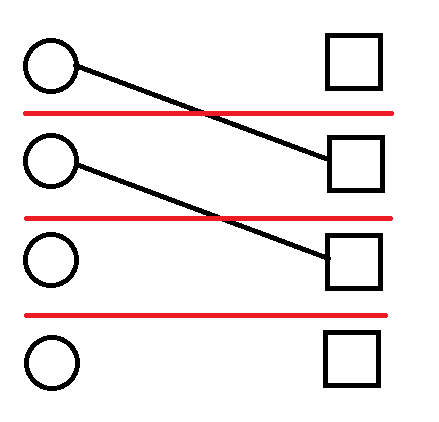
然后我们考虑如何 dp 这个东西，首先肯定有考虑了前 \(i\) 对点，怪异度为 \(j\) 这两个需要记录的量，但是我们考虑转移，发现根本无法计算新产生的怪异度，我们考虑把怪异度的贡献拆到每一条红色的边上，发现此时一条红色边的贡献就是还未匹配的点的数量。

所以此时我们只需要额外记录一个有多少对点还未匹配即可，每次多考虑一对点时，考虑新出现了 \(0/1/2\) 对匹配即可。

时间复杂度 \(O(n^4)\)。

AT_arc176_d Swap Permutation

我们考虑对于我们最后统计答案的一对位置 \((A,B)\)，最后其他数来到这里的概率都是相同的，所以我们把其他数都看成一个等价类 \(C\)，那么最后的概率只有 \(7\) 种：\((A,B),(A,C),(B,A),(B,C),(C,A),(C,B),(C,C)\)。

然后我们发现从一种局面变成另外一种局面的方案数都是一定的，可以写成矩阵形式，这样我们是可以矩阵快速幂计算出每种情况的方案数。

得到方案数后，这个题的计算就变得简单了。

因为只有 \(O(n)\) 个对，直接暴力枚举每个对，计算七种情况的贡献即可。

类似题目：P4223 期望逆序对

CF1060F Shrinking Tree

非常困难的题目。

卧槽，我本来记得这个题非常困难，写着写着发现就是小 D 与随机，然后卡精度，出题人私募了，构式。

考虑计算计算 \(x\) 的答案的时候，考虑以 \(x\) 为根，那么如果一条边是他到根路径上的最后一个收缩的，那么就有 \(\frac 1 2\) 杀了这个根，概率乘上 \(\frac 1 2\)，你发现这个就是小 D 与随机，然后出题人卡精度，私募了。

不想讲其他做法了，大家可以直接看题解。

算了，讲一个神秘做法，我们把排列考虑成 \(n-1\) 个 \([0,1]\) 的随机变量，然后设 \(f_u(x)\) 表示 \(u\) 到根最大值是 \(x\) 的时候系数的期望，则我们枚举这条边的边权为 \(t\)，可以知道：

\[\begin{aligned} f_u(x)=\prod_{v\in son(x)}(\int_0^xf_v(x)\mathrm d t+\frac 1 2\int_x^1f_v(t)\mathrm dt) \end{aligned} \]

答案就是 \(f_{rt}(0)\)，然后直接维护多项式积分和乘法即可，\(O(n^3)\)

P5405 [CTS2019] 氪金手游

有了上面的题的经验，这个题就很简单了。

首先我们考虑一颗叶向树，如果 \(x\) 是子树的根，那么他的贡献是多少，不难知道就是 \(\frac {w_x}{\sum w}\)，原因显然。

然后我们考虑原题，发现有向上和向下的两种边，我们考虑对于向上的边容斥，变成向下的时候有 \(-1\) 的容斥系数，不理他的时候容斥系数为 \(1\)，然后我们就可以 dp 了。

设 \(f_{u,i}\) 表示考虑了 \(u\) 子树内，且 \(u\) 所在子树 \(\sum w\) 为 \(i\) 的情况，那么考虑 \(u\) 的一个儿子 \(v\)。

• \(u\to v\)，此时我们发现直接卷积即可。
• \(v\to u\)，我们考虑是否容斥这一条边，钦定向上的话就是 \(f'_{u,i+j}\gets -f_{u,i}\times f_{v,j}\)，否则是不管他相当于断开这条边：\(f'_{u,i}\gets f_{u,i}\times f_{v,j}\)

注意每次处理完一个节点 \(u\) 后 \(f_{u,i}\) 都要乘上 \(\frac 1 i\)。

CF868E Policeman and a Tree

很厉害的题目。

首先一种想法是我们在某一条点上，暴力状压每个相邻的点有多少人，显然比较爆炸。

考虑把状态弄在边上，然后我们考虑此时只有两个方向，那么我们就可以把状态设置为 \(f_{i,j,k}\) 表示剩下 \(i\) 个人，在第 \(j\) 条有向边上，此时指向方向的连通块有 \(k\) 个点的方案数。

首先设 \(j\) 是 \(u\to v\) 的边，那么：

• \(v\) 是叶子，\(f_{i,j,k}=f_{i-k,j^1,i-k}\)。
• 否则我们考虑 \(v\) 相邻的除去 \(u\) 的点集 \(a_1,a_2,\ldots a_p\)，

\[f_{i,j,k}=\max_{c_1+c_2+\ldots c_p=k}\min_{i=1}^p f_{i,v\to a_i,c_i}+w \]

啊嘞，是不是变量重名了来着，不管了。

首先我们可以归纳知道 \(f_{i,j,i}\le f_{i,j,i-1}\le f_{i,j,i-2}\le \ldots \le f_{i,j,0}\).

然后二分最小值套二分 \(c_i\) 就是 \(O(n^3\log^2 n)\)，但是我们可以做到更加好，我们现在已经知道 \(f_{i,v\to a_i,c_i}\) ，然后拿一个堆维护 \(f_{i,v\to a_i,c_i+1}\) 的最小值，这样我们就可以 \(O(n\log n)\) 统计完所有的 \(f_{i,j,0\ldots i}\)，复杂度 \(O(n^3\log n)\)。

AT_agc056_e [AGC056E] Cheese

首先我们假设我们当前考虑的第一只老鼠，坐标为 \(0.5\)，然后我们可以怎么做呢，首先考虑一个奶酪放在 \(x\) 处的位置，如果 \(x\) 不是 \(0\)，不妨先让他转完一圈，并考虑会不会被吃掉的问题，这个过程可以 dp 计算，记 \(f_{i,j,k}\) 表示考虑到 \(i\)，放了 \(j\) 个奶酪，被吃了 \(k\) 块的概率和。

好，然后现在我们假设有 \(x\) 块奶酪在 \(0\) 处，考虑不被 \(0.5\) 吃的概率：

第一块概率是

\[\sum_{i=0}(\frac {1}{2^{x+1}})(1-\frac 1 {2^x})=\frac {1-\frac 1 {2^x}}{1-\frac 1{2^{x+1}}} \]

所以总概率是：

\[\prod_{i=1}^x\frac {1-\frac 1 {2^i}}{1-\frac 1 {2^{i+1}}}=\frac 1 {2(1-\frac 1 {2^{x+1}})} \]

然后计算答案即可。

CF1810G The Maximum Prefix

首先考虑从前往后做，发现要记录当前权值和当前最大值，很邪恶，考虑倒过来，从后往前做，我们记录当前前缀最大值。

然后我们发现，最前面加入一个数的时候，只需要令当前 \(v\gets \max(v+a_i,0)\) 即可，此时只需要记录一个值了，非常好。

然后我们考虑确定了一个 \(k\) 怎么做，不难发现可以直接 \(O(k^2)\) dp，设 \(f_{i,j}\) 表示考虑到 \(i\)，然后目前最大前缀和是 \(j\) 的概率，统计答案就是 \(\sum_{i=0}^k i\times f_{1,i}\)。

对于一个 \(k\) 计算答案是 \(O(k^2)\) 的，然后考虑对于所有的 \(k\) 怎么做，观察到每次转移都是一样的，最后每个位置对于答案的贡献也是一定的，所以我们反过来 dp，记录 \(g_{i,j}\) 表示 \(f_{i,j}\) 对于答案的贡献系数，然后这样我们只需要一次 dp 就能求出每个位置对于答案的贡献系数，复杂度变成了 \(O(n^2)\)。

CF1988F Heartbeat

首先我们考虑一定的 \(m\) 怎么做，考虑 \(m\) 所在位置，那么左边是不存在后缀最大值的，右边也不存在前缀最大值。

我们考虑 dp 左边方案数，记 \(f_{i,j,k}\) 表示考虑长度为 \(i\) 的序列，有 \(j\) 个前缀最大值，\(k\) 个上升值的方案数。

然后我们考虑转移，如果每次放 \(i+1\) 会推平一段后缀，所以考虑每次加入最小值：

• 加到开头：\(f_{i+1,j+1,k+1}\gets f_{i,j,k}\).
• 加到结尾:\(f_{i+1,j,k}\gets f_{i,j,k}\).
• 加到本来是上升的间隔里:\(f_{i+1,j,k}\gets f_{i,j,k}\times k\).
• 加到不是上升的间隔里:\(f_{i+1,j,k+1}\gets f_{i,j,k}\times (i-1-k)\).

此时的预处理部分是 \(O(n^3)\) 的.

考虑如果统计答案,枚举左边长度 \(i\),左边前缀最大值个数 \(p\),左边上升长度 \(x\),右边长度 \(j\),右边后缀最大值个数 \(q\),上升个数 \(y\).

则不难知道:

\[ans_{i+j+1}\gets \binom {i+j}if_{i,p,x}g_{j,q,y}a_{p+1}b_{q+1}c_{x+y+(i>0)} \]

我们令 \(f_{i,p,x}\gets f_{i,p,x}\times a_{p+1},g_{j,q,y}\gets g_{j,q,y}\times b_{q+1}\)

此时变成了:

\[ans_{i+j+1}\gets \binom {i+j}if_{i,p,x}g_{j,q,y}c_{x+y+(i>0)} \]

发现贡献系数和 \(p,q\) 无关,再把组合数拆开,记录:

\[F(i,x)=\frac 1{i!}\sum_p f_{i,p,x},G(j,y)=\frac 1{j!}\sum_q g_{j,q,y} \]

然后我们把 \(i>0\) 限制分成两部分,\(i=0\) 暴力处理即可,只考虑剩下的部分.

得到:

\[\frac 1 {(i+j)!}ans_{i+j+1}=\sum_i\sum_x\sum_j\sum_y F(i,x)G(j,y)c_{x+y+1} \]

首先发现我们可以二维 NTT,但是 poly 是邪恶的,放弃这一部分.

然后我们发现，似乎 \(i\) 和 \(y\) 没有一点关系，考虑在枚举 \(i\) 时不枚举 \(y\)，预处理 \(t_{x,j}=\sum_y G(j,y)c_{x+y+1}\)。

然后此时转移变成了 \(\frac 1 {(i+j)!}ans_{i+j+1}=\sum_i\sum_x\sum_j F(i,x)t(x,j)\)

然后计算即可，时间复杂度 \(O(n^3)\)。

AT_ddcc2017_final_d なめらかな木

首先我们应该有一个 \(f_{i,u,v,S}\) 的做法，表示考虑了 \(i\) 个点，\(i-1,i\) 对应节点分别是 \(u,v\)，填数集合是 \(S\) 的方案数。

因为 \(|S|=i\)，所以状态数是 \(O(n^22^n)\) 的，看起来不大能过的样子。

我们考虑再发掘一些性质，首先每个点度数 \(\le 4\)，否则一定无解。

所以我们考虑删掉任意两个点之后只会剩下最多 \(7\) 个连通块。

然后我们考虑这些连通块有什么性质，不难发现要么全填过数了要么全都没有填过数，否则一定不合法。

那么此时对于连通块状态状压，状态数实际上只有 \(O(n^2\times 2^7)\)，转移是 \(O(n)\) 的，复杂度 \(O(n^3\times 2^7)\)。

QOJ9561 树数叔术

首先我们挖掘一下性质：

• \(0\) 只有一个。
• 每种权值都必须出现。

所以我们可以只计算 \(V\le n\) 的数据。

然后考虑对于每种权值 \(i(i>0)\) 找找性质，由于有 \(\text{mex}\)，所以我们考虑 \([0,i]\) 形成的虚树，考虑什么条件是合法的：

手玩后发现是下面两种情况满足一个就合法：

• \(i\) 只出现 \(1\) 次。
• 不存在 \(i\) 是虚树叶子。

然后考虑 dp，我们先计数不带编号的，最后乘上 \(n!\) 即可。

设 \(f_{i,j,k}\) 表示考虑了 \([0,i]\) 权值，虚树大小为 \(j\)，有 \(k\) 个点是虚树上还未分配权值的点。

然后分成 \(i\) 是叶子和不是叶子转移。

• \(i\) 是叶子

  • 是某个节点连出来的： \(f_{i+1,j+1,k}\gets f_{i,j,k}\times j\)。
  • 是某条边连出来的；\(f_{i+1,j+2,k+1}\gets f_{i,j,k}\times (j-1)\)。

• \(i\) 不存在叶子，枚举树边插入了 \(p\) 个点，给未分配权值的分配了 \(q\) 个，则 \(f_{i+1,j+p,k-q}\gets f_{i,j,k}\binom k q\binom {j+p-2}{j-2}\)，注意此时要满足 \(p+q>0\)。

答案是 \(n!f_{V,n,0}\)。

然后直接 dp 是 \(O(n^5)\)，但是可以直接 \(1s\) 内通过/jy

考虑如何优化，不难发现 \(i\) 不存在叶子部分是重点，考虑优化这个部分。

不难发现此时贡献系数 \(p,q\) 独立，考虑分步转移即可，复杂度降至 \(O(n^4)\)。

AT_tdpc_grid マス目

首先看到 \(H\le 6\) 的限制，不难想到状压，然后我们发现一列只有不超过 \(3\) 个连通块，然后我们考虑给每列标注一种状态，首先不能走的位置是 \(0\)，然后跟 \(1\) 连通的位置记作 \(1\)，剩下的连通块从下标从小到大记作 \(2,3\)，转移时枚举下一列的格子颜色，复杂度 \(O(m8^n)\)，大概可以过。

但是发现应该状态数根本没到 \(4^n\)，搜一下发现只有 \(S=200\) 左右，预处理出下一位每种情况的转移，复杂度降至 \(O(m2^nS)\)，非常快，发现这个转移是递推形式，然后直接矩阵快速幂 \(O(S^3\log m)\)，可以把 \(m\) 开到 \(10^9\)。