网络流学习笔记

首先是单纯形算法，大概是先找出一颗支撑树作为基，然后从 \(S\to T\) 连一条流量为 INF，费用为 -INF 的边，在上面不断找负环推流，这个东西跟 EK 相似，相当于每次找一条边增广，但是差别是不一定每次增广的是费用最小的路径，即过程不具有凸性。

扔个板子：

namespace MCMF{
	const int N=3e4+50,M=2e4+50,INF=1e6;
	struct Edge {
		int u,v,nxt,f,w;
	}E[N];
	int h[M],tot=1;
	inline void addedge(int u,int v,int f, int w=0){
		// cerr<<u<<" "<<v<<" "<<f<<" "<<w<<"\n";
		E[++tot]={u,v,h[u],f,w},h[u]=tot;
		E[++tot]={v,u,h[v],0,-w},h[v]=tot;
	}
	int pre[M];
	int f[M],fw[M],cir[M],tag[M];
	int Now,S,T;
	inline void build(int x,int e, int now=1){
		fw[x]=e,f[x]=E[e].u,tag[x]=now;
		for(int i=h[x];i;i=E[i].nxt) 
			if(tag[E[i].v]!=now&&E[i].f) build(E[i].v,i,now);
	}
	inline int Sum(int x){
		if (tag[x]==Now) return pre[x];
		tag[x]=Now,pre[x]=Sum(f[x])+E[fw[x]].w;
		return pre[x];
	}
	inline int calc(int x){
		int rt=E[x].u,lca=E[x].v,cnt=0,id=0,fl=2;
		++Now;
		while(rt) tag[rt]=Now,rt=f[rt];
		while(tag[lca]!=Now) tag[lca]=Now,lca=f[lca];
		int F=E[x].f,cost=0;
		for(int u=E[x].u;u!=lca;u=f[u]){
			cir[++cnt] = fw[u];
			if (F>E[fw[u]].f)  F=E[fw[u]].f,id=u,fl=0;
		}
		for(int u=E[x].v;u!=lca;u=f[u]){
			cir[++cnt]=fw[u]^1;
			if (F>E[fw[u]^1].f) F=E[fw[u]^1].f,id=u,fl=1;
		}
		cir[++cnt]=x;
		for (int i=1;i<=cnt;++i) 
			cost+=F*E[cir[i]].w,E[cir[i]].f-=F,E[cir[i]^1].f+=F;
		if(fl==2) return cost;
		int u=E[x].u,v=E[x].v;
		if(fl==1) swap(u,v);
		int Lste=x^fl,Lstu=v,Tmp;
		while(Lstu!=id)
			Lste^=1,--tag[u],swap(fw[u],Lste),
			Tmp=f[u],f[u]=Lstu,Lstu=u,u=Tmp;
		return cost;
	}
	int cost;
	inline int Simplex (){
		memset(f,0,sizeof f);
		addedge(T,S,INF,-INF),build(T,0,++Now),tag[T]=++Now,f[T]=0;
		bool fl=1;
		while(fl){
			fl=0;
			for(int i=2;i<=tot;++i) 
				if(E[i].f&&E[i].w+Sum(E[i].u)-Sum(E[i].v)<0) cost+=calc(i),fl=1;
		}
		cost+=E[tot].f*INF;
		return E[tot].f;
	}
	#define S MCMF::S
	#define T MCMF::T
	#define add MCMF::addedge
	#define INF MCMF::INF
}using MCMF::N;

P4701 粘骨牌

我们将棋盘黑白染色，设 \((1,1)\) 是黑色的，我们发现，空出来的点一定是黑色的，然后我们考虑 \(S\) 往空点连边，对于不能露出的点，我们将其往 \(T\) 连边，然后对于一个白点，若他所在骨牌可以移动，相当于空白可以从一个黑点跳到另一个黑点，费用为固定这个骨牌的费用，然后求最小割即可。

P4003 无限之环

我们发现，每个水管都需要一个入水口和一个出水口，所以我们考虑黑白染色，然后旋转的费用我们分讨一下即可得出，判断有无解只需要知道最大流是不是总水管口数量的一半即可。

P3965 循环格

我们发现，如果要出现循环，即每个格子的出入度都要为 \(1\)，那么我们拆点，对本来方向的点连流量为 \(1\) ，费用为 \(0\) 的边，剩下的三个方向连流量为 \(1\)，费用为 \(1\) 的边。

然后跑最小费用最大流即可。

区间选择

给定 \([1,n]\) 中的 \(m\) 个区间 ，每个区间 选择一次 的代价为 \(w_i\)，最多选 \(p_i\) 次

要求使 任意点 \(j\) 被选择的次数在 \([l_j,r_j]\) 之间，求 代价最值

我们先建立一条长度为 \(n+1\) 的链，考虑对于 \((j,j+1)\) 这条边的流量，表示 \(j\) 被选择的次数，然后对于一个 \([L,R]\) 的区间，我们从 \(L\) 往 \(R+1\) 连一条流量为 \(p\)，代价为 \(w\) 的边，表示这个区间被选一次。

然后我们不妨设总流量为 \(F\)，那么第 \((i,i+1)\) 的上下界就是 \([F-r_i,F-l_i]\)，跑上下界网络流即可。

P6967

我们不妨假设猫咪每个时间都在睡觉，那么我们可以得到每一个长度为 \(k\) 的区间需要吃饭的时间，而每个时间猫猫吃饭都会有一个贡献，且会让一段长度为 \(k\) 的区间的吃饭时间 +1，这就转化成了上面的问题。

P4134

我们考虑拆点后暴力连边，然后费用为 \(x+y\)，流量为 \(1\)，但是我们要怎么保证不会出现 \(x\to y'\) 和 \(y\to z'\) 同时出现呢，我们发现，因为费用对于一个 \(y\) 来说两两不同，我们会匹配到 \(x\to y'\) 和 \(y\to x'\)，然后我们就可以把费用除 \(2\) 即可。

P4542

这个限制就很坏，我们考虑如何去掉，首先假设我们有一个点在 \(x\)，然后要去 \(y\) 把这个点爆了，那么我们的最短路就是不经过编号超过 \(y\) 的点的最短路，这个我们可以用 Floyd \(O(n^3)\) 求出来新图中的两两距离，然后我们可以发现，现在问题转化成了需要 \(k\) 条路径，使其并为全集。

我们还是拆点，然后我们对于 \(i\to i'\) 连一条费用 -INF，流量 \(1\)，和费用为 \(0\)，流量为 INF 的边，这样因为我们需要最小费用，就一定会流过每个点，最后费用加上 \(n\times \text{INF}\) 即可。

P4486

我们考虑将每个点抽象成边，然后他会造成贡献的格子抽象成点，且把所有格子先变成最小的可行值，然后我们跑最小费用可行流即可。

CF1383F

有点牛的题，我们考虑最大流 = 最小割，由于 \(k\le 10\)，我们不妨枚举有哪些特殊边为割边，以及此时的最小割。

我们发现，对于假设我们枚举了 \(S\) 为割边集合，那么把 \(S\) 内的边权设为 \(0\)，非 \(S\) 设为 INF，跑最大流即可。

然后我们我们发现，一个 \(S\) 一定是在一个 \(S'\) 的基础上修改一条边而来，我们可以每次记录 \(S'\) 的残量网络，然后跑 EK 或者 单纯性这种每次增广一条边的算法。

然后对于询问，枚举割集，找到最小割，这个就是询问的答案。

P3347

第一问是简单的。

对于第二问，我们对函数求导即可知道单位函数的代价是 \(2ax+b\)，不妨设函数 \(f(x)=y\) 表示当单位费用不超过 \(x\) 时，我们的最大流量是 \(y\)，然后我们发现这个函数一定是凸的，且只有 \(O(n)\) 段，如图所示：

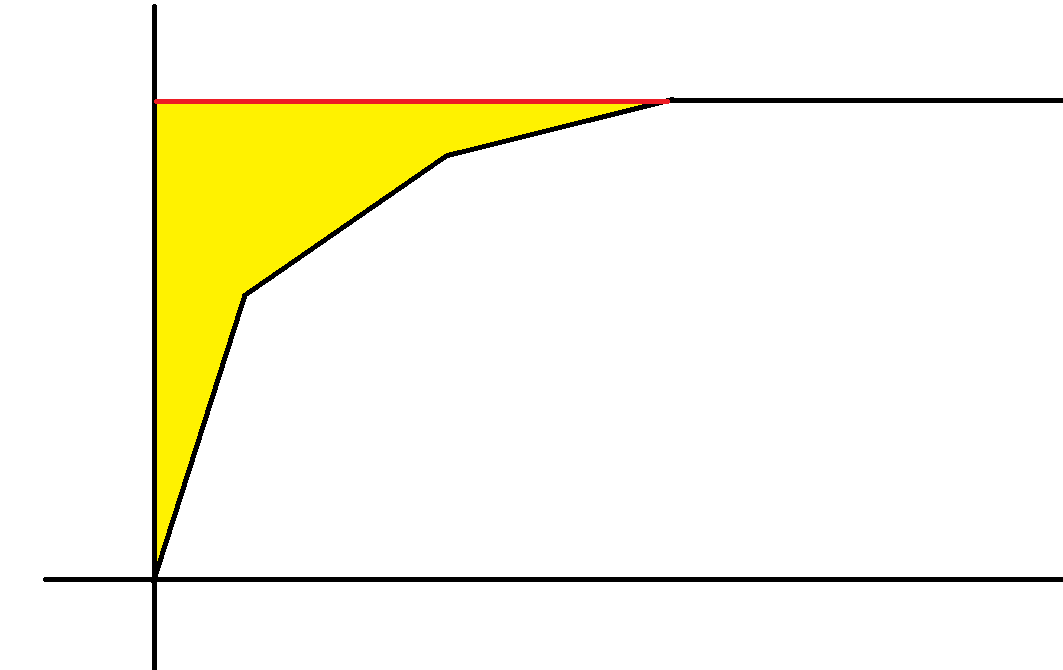
黄色部分就是我们的最小费用。

我们考虑了如何求出这个这个函数，首先我们应该能知道边界的两个线段，且我们对于一个 \(x\) 我们可以以跑一次最大流的代价求出 \(f(x)\)。

我们考虑如何找出所有的断点，我们先找出边界的两个线段的交点，如果在一条线段上说明这是唯一的断点，否则说明我们中间还有若干段函数，分治下去找即可。

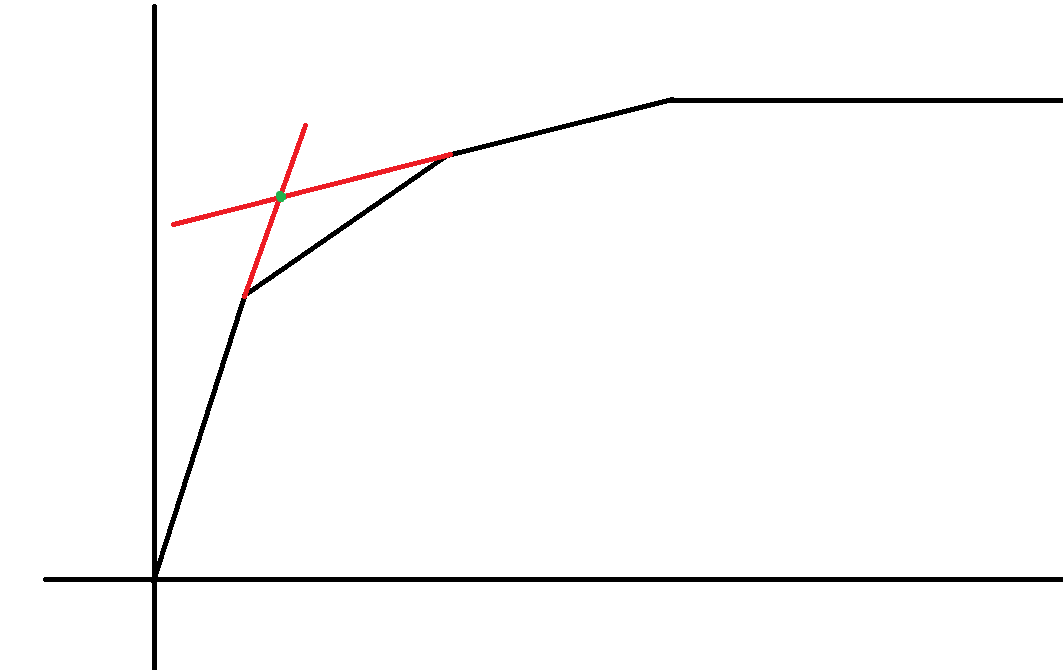
由于防止出题人卡，我们也许需要一些微扰，比如加上 eps 之类。

然后求出断电后，求面积是简单的。