BUUCTF—Crypto（完结版本—_—）

BUUCTF—Crypto

1.一眼就解密

考点：base64

我的解答：

字符串后面的等号，看来是base大家族，由字母和数字范围来看是base64，不管了，先扔CyberCher，仙女魔法棒变出flag。

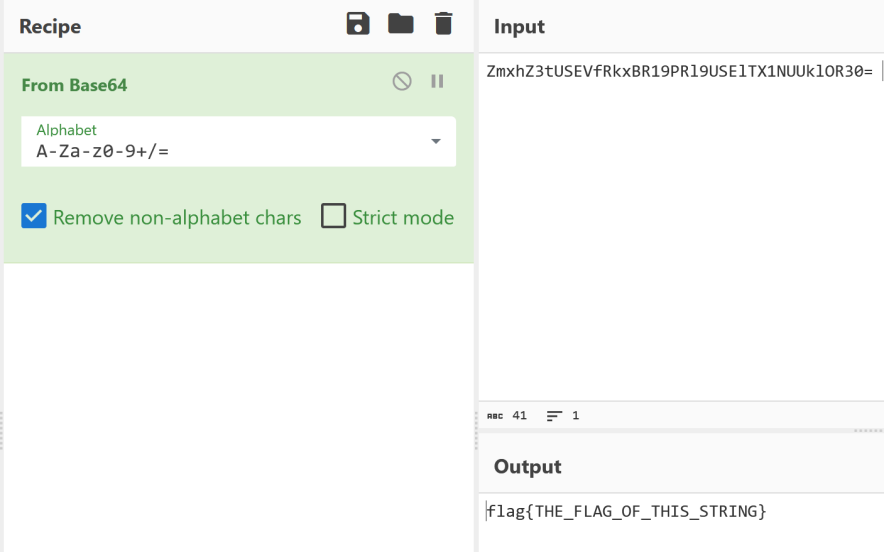
2.MD5

考点：MD5

我的解答：

打开文件出现一串由数字和字母拼出的字符串，MD5的特征：长度为32或16。由题目名提示MD5，得出为MD5解密，打开工具解密

成功解出flag内容，复制上交一条龙。

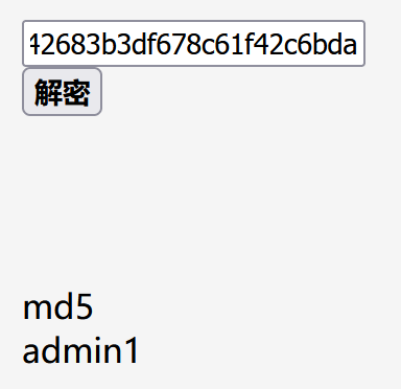
3.URL编码

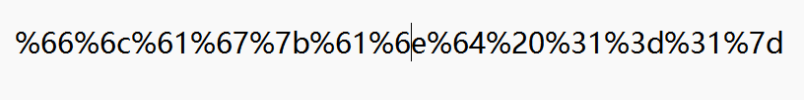
考点：URL编码

我的解答：

下载文件，打开text。%间隔，是百分号编码，标准的URL，用工具进行解码直接得出flag

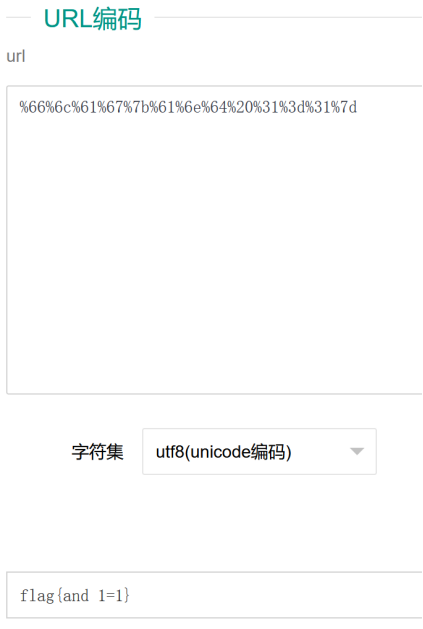
4.看我回旋踢

考点：词频分析Quipqiup）

我的解答：

有大括号，前面四个字母，标准的flag格式，猜测是凯撒，synt转为flag，都位移为13，直接放入凯撒解码脚本，当然，还有工具也是可以滴。

进行凯撒解密，得出flag

5.摩丝

考点：摩斯密码

我的解答：

光题目就猜测是莫斯，给了题目，这个点和杠，标准的莫斯密码咧。哎嘿！

立刻复制粘贴，工具工具！转出flag

进行输入flag{iloveyou}，豁！错误，试试大写，flag{ILOVEYOU}。nice！大写通过！

6.passwork

考点：古典密码

我的解答：

题目……题目给了这个东西。姓名和生日，key有什么意义不？先直接勇敢尝试张三+19900315，不出所料的出错了。加密试试，AES？出不来，Rabbitt也出不来。

尝试了key{zs19900315}，错误，可能是顺序不对，把zs移到到后面也不对。开始迷茫，突然不知道怎么着，去改了下key，感觉还是flag。好家伙，flag{19900315zs}，最后给我个烟雾弹，我真的，哭死。（这道题真的想了段时间）

7.Quoted-ptintable

考点：Quoted-printable

我的解答：

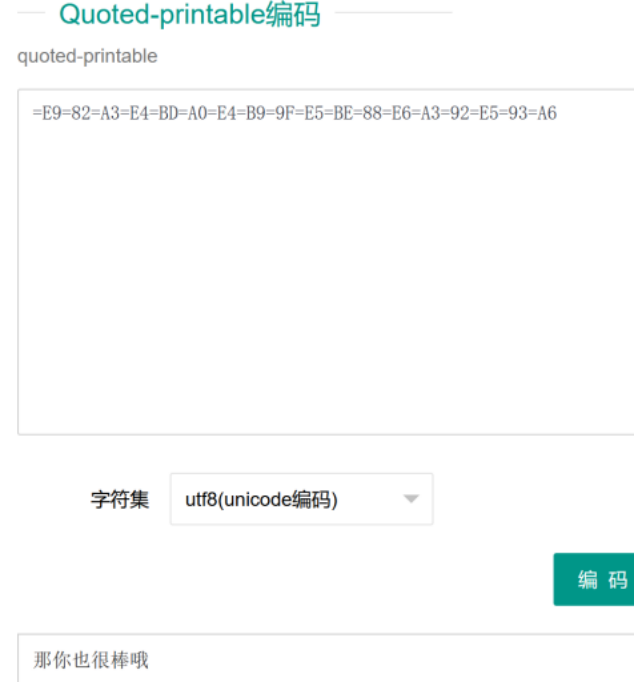
开题目，等号，嘿嘿，记得这个密码，找工具。

但是我不知道这类密码叫啥了，看了下知识点，是我没落实到位，就是题目名字Quoted-printable（尴尬.jpg，小丑竟是我自己）。直接工具解码，flag出来了。

8.Rabbit

考点：Ribbit加密

我的解答：

这题目，盲猜一波是兔子密码，打开题目，固定U2Fs……开头，红烧兔肉我来啦！

直接工具解密

9.篱笆墙的影子

考点：栅栏密码

我的解答：

打开题目，是长串字符串，题目叫篱笆墙的影子，篱笆对应栅栏，说明是栅栏加密。还有一方面是因为有大括号，但是前面的字数不对，可能是移位，栅栏加密大概率符合。

加密几位不是很清楚，题目给了一大串的中文歌词，去搜了下，是我孤若寡闻了，那个歌词的歌曲名字就叫篱笆墙的影子,没找出到底是移了几位。

打开了随波逐流，直接用栅栏解密进行暴力破解，出来啦！

10.RSA

考点：RSA，素数解码

我的解答：

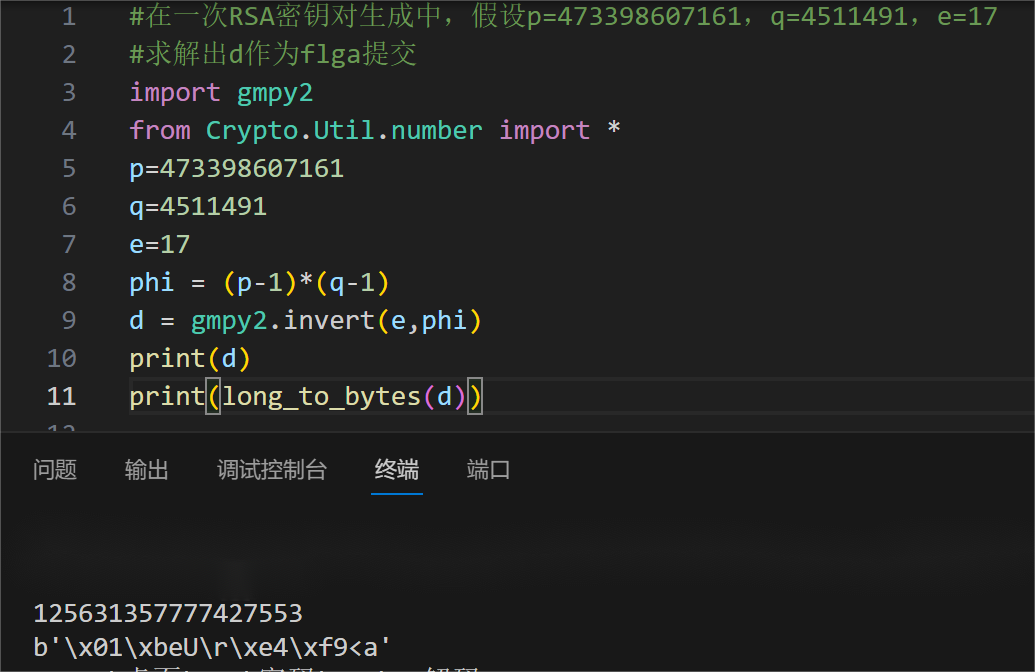
标准的RSA解码，给出了p，q还有e，d的取值就很简单

发现d只能是数字，而不能转换成字符串。那就flag放数字，没出错。

11.Alice与Bob

考点：RSA，大数分解

我的解答：

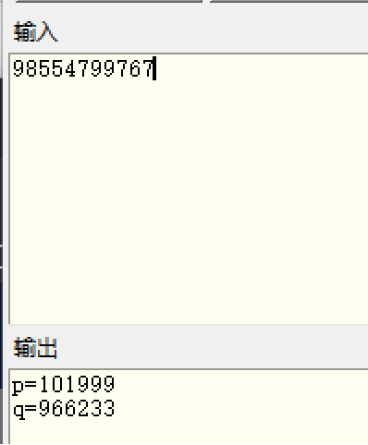
按照题目所说，用分解工具进行素数分解

得出的p、q将小的方前大的放后组成新的数字，放入MD5的加密，进行32为小写加密得出flag内容：（两位伟大的爱情值得歌颂，坚定.jpg）

12.大帝的密码武器

考点：凯撒密码

我的解答：

我滴妈！给了一个不知道什么格式的文件，我直接用txt打开时乱码

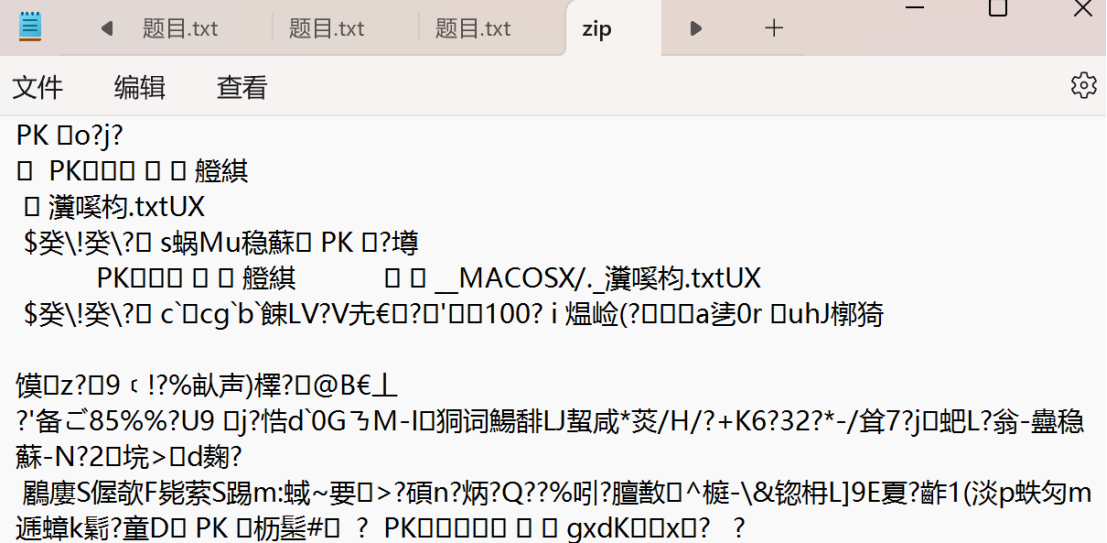
尝试了vscode，还是失败了。然后因为文件名称是zip（师傅指导说是因为文件头是PK，是典型的压缩包头格式）是压缩包格式，尝试改变了文件格式，出来了一个可以成功打开的压缩包。

Zip尝试成功，给出两个txt文件

涉及罗马，那就是凯撒加密，需要把给出的FRPHEVGL进行解密随波逐流出动

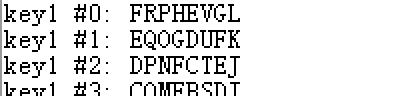
说真的，英语不好的我伤不起，改成了小写，因为大写太陌生了#.#。

小写找到了，key为13

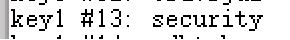
然后用第二个文本中的字符进行凯撒加密，得出flag。

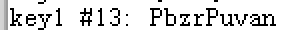
13.rasrsa

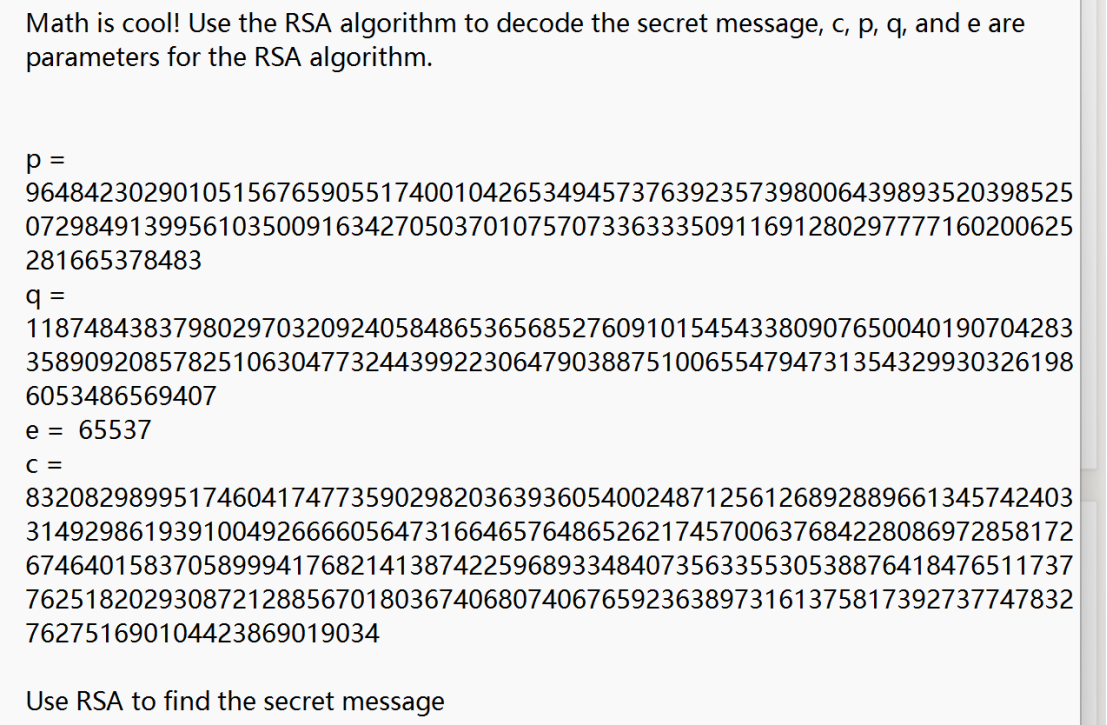
考点：RSA大素数解码

我的解答：

RSA的明显提示，有p、q、e、c，复制黏贴放入大素数解码的vscode脚本。

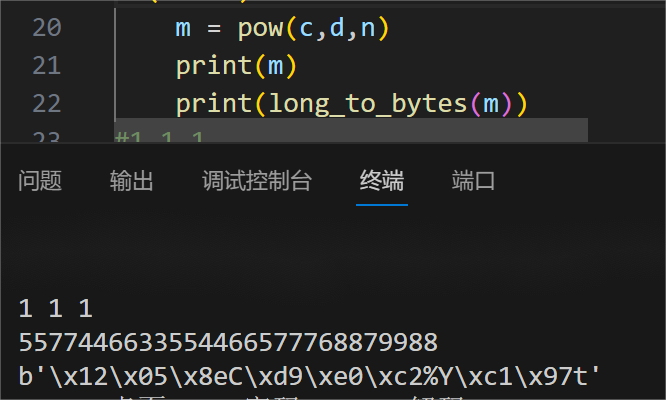
发现m求出数据只能是数字，不能转为字符串我自我怀疑了一下，但是值都是互素没有问题，我觉着可以用m本身尝试一下，没有出错，这次的m是数字

14.萌萌哒的八戒

考点：猪圈密码

我的解答：

这道题我直接连题目都打不开了@=@

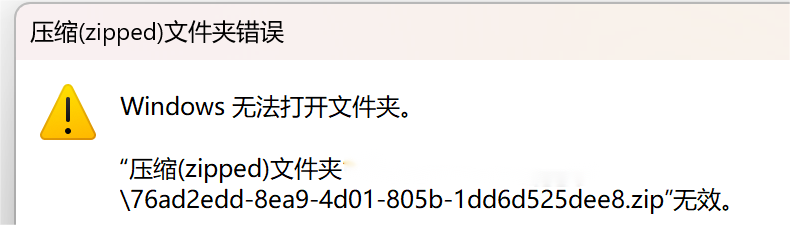
既然是压缩文件夹出错，我找到了我下载的文件换了个压缩方式打开了

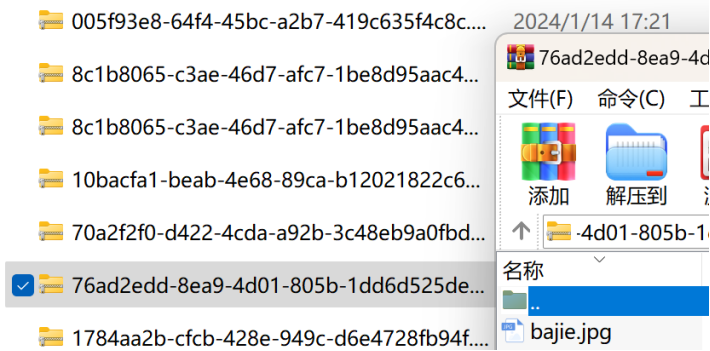
打开图片，是一只猪猪，图片下面明显有密码图案，是猪圈密码，直接查表得。

15.old-fashion

考点：词频分析

我的解答：

一段英文的乱文，直觉告诉我flag应该是最后的那串奇奇怪怪的东西，但是我不太能想到是什么加密。

凯撒硬破解还是乱文，不是凯撒。？= ？栅栏更不是。

实在不会，我去找了找解答，新知识点：词频分析，给了暴力破解的网站，Quipqiup网站。解出来一大串，有两种flag，都是一遍，第一个就是。

16.Unencode

我的解答：

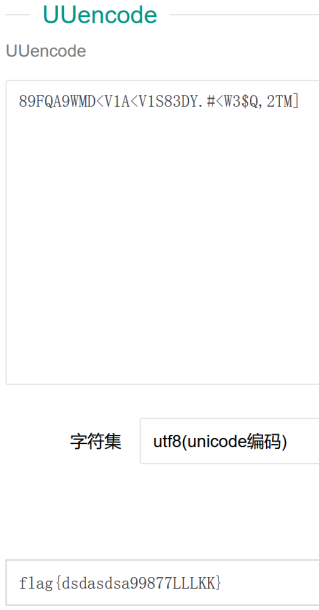
这题出来了以下内容，我一时半会儿没想出来，好像没有什么符合这个字符串。

没有思路去找了古典密码的博客，看见了一个加密类型叫UUencode，找工具就能直接解码。

17.[AFCTF2018]Morse

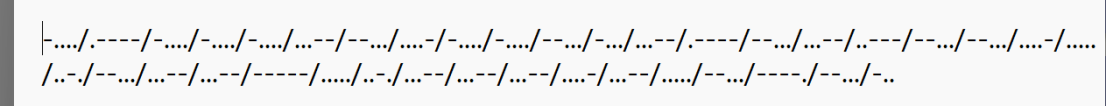
考点：摩斯密码

我的解答：

标准的莫斯密码，把斜杠换成空格，方便解码

解码出来是长串的数字和几个英文字符，猜测是16进制

使用魔法棒，自动转换出flag，是十六进制转换成ASCII码

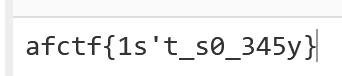
18.变异凯撒

考点：凯撒加密

我的解答：

由题目可得为凯撒加密，稍微变换一下

用脚本，把开头固定的flag对应的四位进行计算，得出后退的大小从5开始逐渐递增。

（师傅提醒也可以用随波逐流直接解密的）

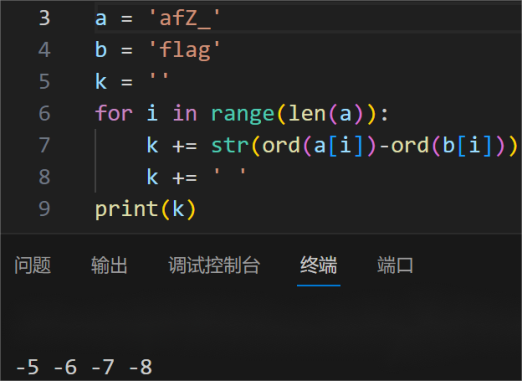
开始写脚本，进行解码，得出了flag

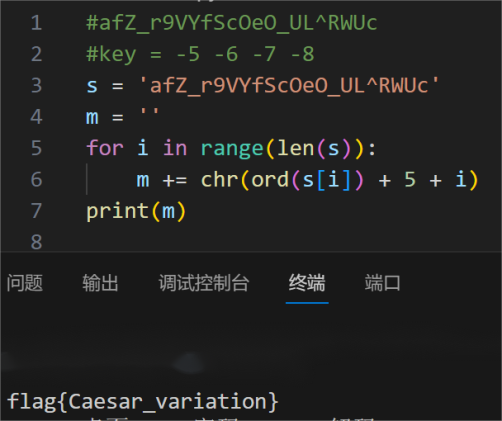
19.丢失的MD5

考点：MD5加密

我的解答：

哇！代码加密？MD5不可逆转，但是这个代码出错了！

输出错误改正，但是下面这个，看不懂。百度百科一下下

哦，找到了修改方法，需要把Unicode字符串改为字节，在后面统一加上.encode(‘utf-8’)

运行代码，成功输出字符，flag，我来了。

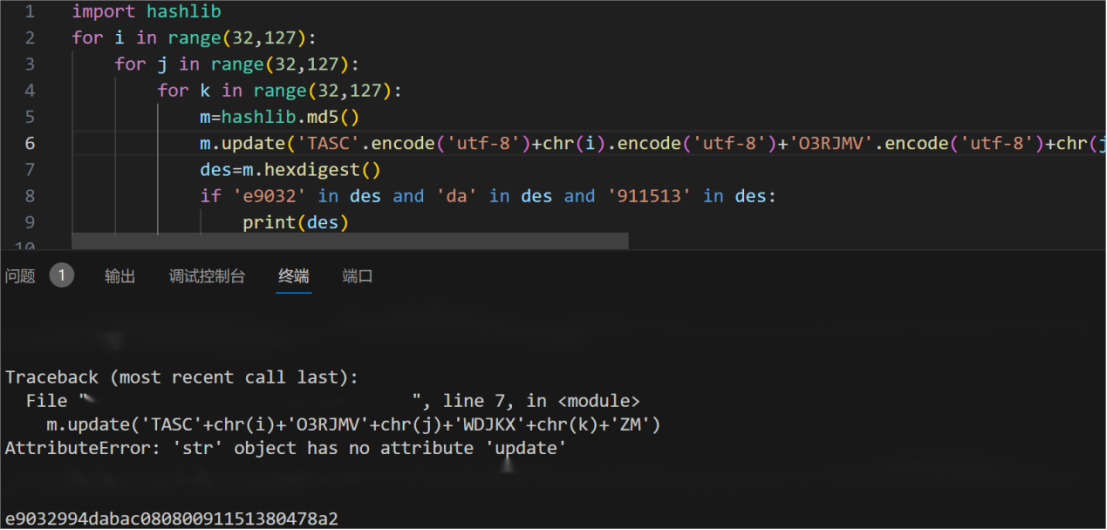
20.Windows系统密码

考点：哈希加密，MD5解密

我的解答：

我大大眼睛里面是大大的迷惑，这啥呀？*_*

没头绪，但是文件尾缀很奇怪

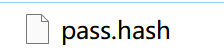
hash去搜了下，是哈希算法，果然，我是个傻叉# . #

既然是哈希算法，那尝试下MD5加密，好像要尝试好多次啊。一个都不行了。

求助于师傅！尝试解码，八段字符串，师傅说看提示，那就是ctf：第二段。前面有重复的，后面是独苗，盲猜是后面的。工具解码：

出来了出来了，嘿嘿 ==^==

21.信息化时代的步伐

考点：中文电报码

我的解答：

题目给提示flag是一串中文

啊哦，是一串字符，试试进制转换，没试出来。

（在线网址：https://dianma.bmcx.com/）

进行大海捞针，扔进随波逐流，一眼看见了相当不合群的中文，鹤立鸡群嗷。新学一个加密：中文电报码，四个数字表示一个中文字。

22.凯撒？替换？呵呵！

考点：词频分析

我的解答：

凯撒试过了。。。没有规律可言。

那就替换试试，进行爆破，工具出来的第一句就是flag，去掉空格就有了（写不出来啊，还是找的题目，看见是密码替换可以用爆破工具，我直接跑入了凯撒的坑一去不复返了）

23.权限获得第一步

考点：MD5解密

我的解答：

让我来看看是啥题目，熟悉的题目！第三题的Windows系统密码，一模一样的形式，嘿嘿（猥琐.jpg）

来来来，重复下解题过程，扔进MD5解密工具。两个密文，按顺序，第一个出来结果是乱文，不要慌，第二个启动！Flag出来了！那个3617656。

24.传统知识+古典密码

考点：古典密码和凯撒加密

我的解答：

两个包，我有点迷茫

提示：

（随波逐流天干地支解码XZSDMFLZ。或写脚本“+甲子”代表每个数字再加60，分别为：88 90 83 68 77 70 76 90。每个数字对应的ASCII码值为：XZSDMFLZ）

第二个文件里面，出处都感觉是十六进制转换，但是转不了咧，提示：曼联，没有头绪，想去看复联了---_---（最后才发现其实这个文件就是来混淆视听的）

还是师傅给的提示：[然后将XZSDMFLZ，先栅栏（key=2)，再凯撒（key=5)，得到结果：SHUANGYU。至于先栅栏还是先凯撒顺序无所谓]

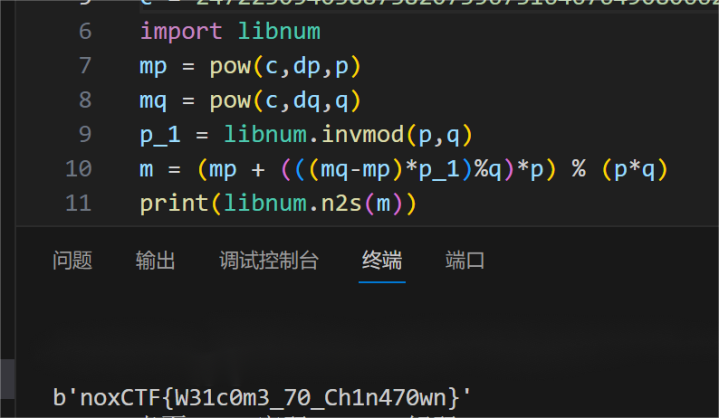
25.RSA1

考点：RSA，dp、dq泄露

我的解答：

打开我亲爱的小题目，dp，dq还有n，c，q，p。看见dp和dq

Emmm，dp，dq泄露，找我滴脚本

把题目中的信息复制入我的脚本，当当当，flag出来了！

26.世上无难事

考点：词频分析、密码爆破

我的解答：

题目是熟悉又陌生的乱码，掏出我的那个词频分析

列表第一个，我看见你了，the key is……，我竟然能看懂，太感动了

复制黏贴——错误，嗯？哦~~题目上表示是小写字母，把大写转成小写，成功！

27.RSA2

考点：RSA，dp泄露

我的解答：

哈！有dp，dp泄露，脚本脚本脚本。

传统形式的dp泄露，成功出flag

28.RSA3

考点：RSA、共模攻击

我的解答：

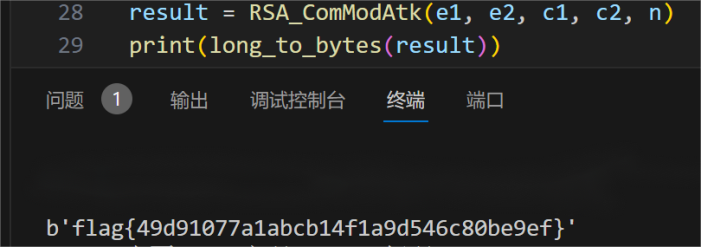
txt中出现了c1,c2,e1,e2,n，RSA中的共模攻击

放入脚本内，运行出现flag

29.还原大师

考点：MD5

我的解答：

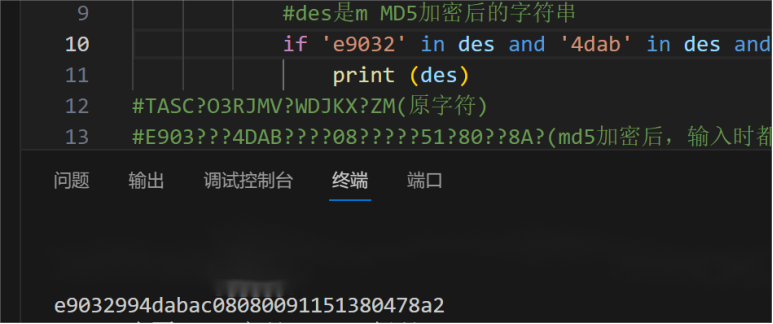
咱就是说，那个去恢复题目丢失的MD5的我真的很狼狈

进行代码改动，换掉需要查找的字符，最后找出加密后的字符串，不能用大写字符进行查找

最后输入flag时，出现了错误，是我忘记把小写改成大写了。所以如果是小写，记得改成大写我总是跳这种坑T_T

30.异性相吸

考点：二进制转换？异或，进制转换

我的解答：

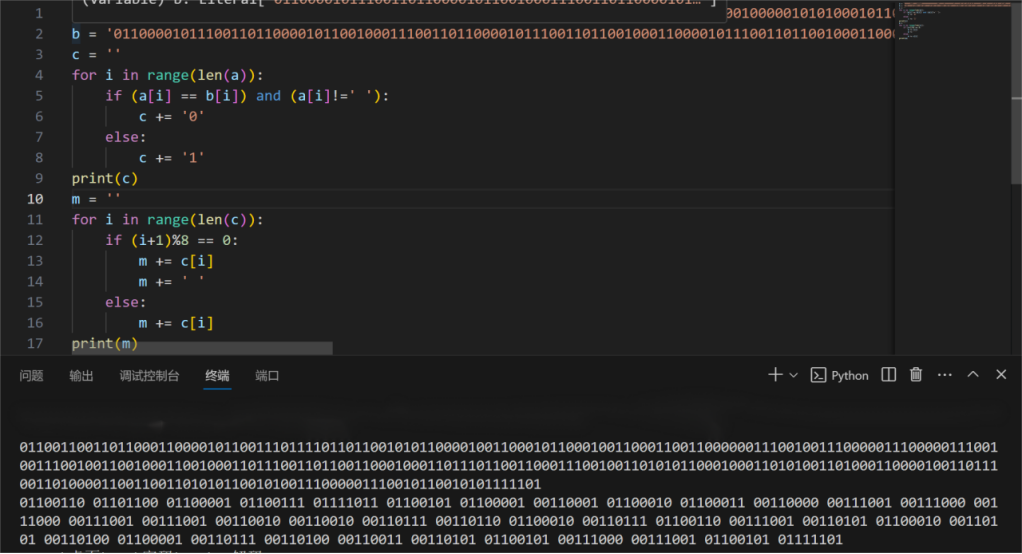
没有头绪的一道题，师傅说转为二进制，观察长度，长度一样，进行异或。写好异或代码，输出是连续的01，在进行8位分割，输出异或后的二进制

hint:互相吸引你可知什么是疑惑

放入进制转换工具，出现flag

31.RSAROLL

考点：RSA多组c

我的解答：

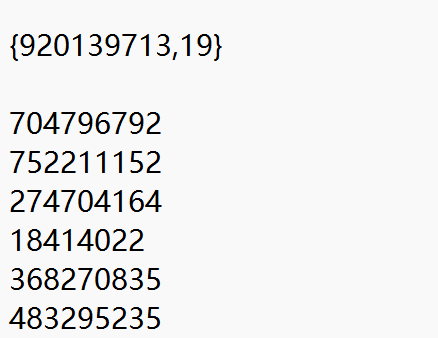
是我那伟大的师傅提醒，n和e是前面大括号里面的数据，下面一连串是c的可能，需要进行逐个尝试

n可以用分解工具分界出p和q

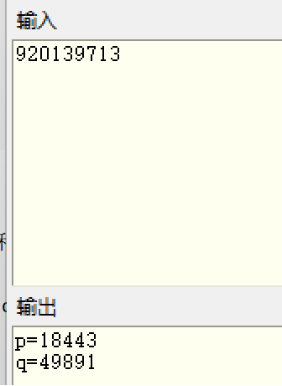
按照师傅所说，打开文件建立列表储存c的全部值，采用for循环进行挨个解密，能发现flag是所有c破解出来拼起来的。flag{13212je2ue28fy71w8u87y31r78eu1e2b}

32.RSA

考点：公钥解密，RSA

我的解答：

师傅滴提示：公私钥？

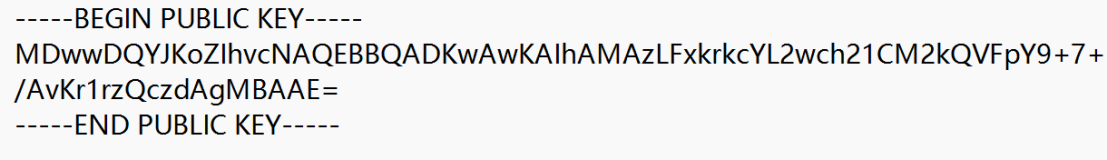
遇事不决百度百科

然后我在工具包里找到了公钥解析的工具，放进去出来了这个。出现了e,n，去分解q,p

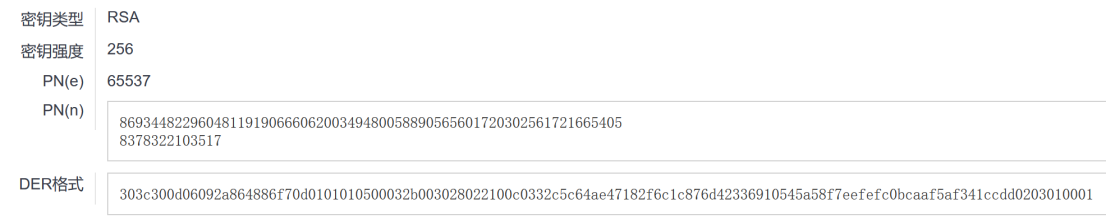
把其中的n进行分解出q和p，但是发现没有c。

询问师傅，给出了代码，需要打开文件。

[MRCTF2020]babyRSA

题目：

import sympy
import random
from gmpy2 import gcd, invert
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
from z3 import *
flag = b"MRCTF{xxxx}"
base = 65537


def GCD(A):
    B = 1
    for i in range(1, len(A)):
        B = gcd(A[i-1], A[i])
    return B


def gen_p():
    P = [0 for i in range(17)]
    P[0] = getPrime(128)
    for i in range(1, 17):
        P[i] = sympy.nextprime(P[i-1])
    print("P_p :", P[9])
    n = 1
    for i in range(17):
        n *= P[i]
    p = getPrime(1024)
    factor = pow(p, base, n)
    print("P_factor :", factor)
    return sympy.nextprime(p)


def gen_q():
    sub_Q = getPrime(1024)
    Q_1 = getPrime(1024)
    Q_2 = getPrime(1024)
    Q = sub_Q ** Q_2 % Q_1
    print("Q_1: ", Q_1)
    print("Q_2: ", Q_2)
    print("sub_Q: ", sub_Q)
    return sympy.nextprime(Q)


if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_p : 206027926847308612719677572554991143421
P_factor : 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
Q_1:  103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2:  151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q:  168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Ciphertext =  1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832
'''

题解：

对P和Q进行自定义函数设置

对gen_p进行解码，n是17个连续素数组成，知道第九个素数，对p进行了RSA加密，求出P

P_factor = 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
P = [0 for i in range(17)]
P[9] = 206027926847308612719677572554991143421

for i in range(10,17):
    P[i] = sympy.nextprime(P[i - 1])
for i in range(8, -1, -1):
    P[i] = sympy.prevprime(P[i + 1])
n_p = 1
phi_p = 1
for i in P:
    n_p *= i
    phi_p *= (i-1)
d_p = gmpy2.invert(base,phi_p)
p = pow(P_factor,d_p,n_p)
p = sympy.nextprime(p)

gen_q加密，简单rsa的加密

Q_1 = 103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2 = 151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q = 168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Q = pow(sub_Q,Q_2,Q_1)
Q = sympy.nextprime(Q)

整体解码

import sympy
from gmpy2 import *
from Crypto.Util.number import *
base = 65537

P_factor = 213671742765908980787116579976289600595864704574134469173111790965233629909513884704158446946409910475727584342641848597858942209151114627306286393390259700239698869487469080881267182803062488043469138252786381822646126962323295676431679988602406971858136496624861228526070581338082202663895710929460596143281673761666804565161435963957655012011051936180536581488499059517946308650135300428672486819645279969693519039407892941672784362868653243632727928279698588177694171797254644864554162848696210763681197279758130811723700154618280764123396312330032986093579531909363210692564988076206283296967165522152288770019720928264542910922693728918198338839
P = [0 for i in range(17)]
P[9] = 206027926847308612719677572554991143421

for i in range(10,17):
    P[i] = sympy.nextprime(P[i - 1])
for i in range(8, -1, -1):
    P[i] = sympy.prevprime(P[i + 1])
n_p = 1
phi_p = 1
for i in P:
    n_p *= i
    phi_p *= (i-1)
d_p = gmpy2.invert(base,phi_p)
p = pow(P_factor,d_p,n_p)
p = sympy.nextprime(p)

Q_1 = 103766439849465588084625049495793857634556517064563488433148224524638105971161051763127718438062862548184814747601299494052813662851459740127499557785398714481909461631996020048315790167967699932967974484481209879664173009585231469785141628982021847883945871201430155071257803163523612863113967495969578605521
Q_2 = 151010734276916939790591461278981486442548035032350797306496105136358723586953123484087860176438629843688462671681777513652947555325607414858514566053513243083627810686084890261120641161987614435114887565491866120507844566210561620503961205851409386041194326728437073995372322433035153519757017396063066469743
sub_Q = 168992529793593315757895995101430241994953638330919314800130536809801824971112039572562389449584350643924391984800978193707795909956472992631004290479273525116959461856227262232600089176950810729475058260332177626961286009876630340945093629959302803189668904123890991069113826241497783666995751391361028949651
Q = pow(sub_Q,Q_2,Q_1)
Q = sympy.nextprime(Q)

Ciphertext =  1709187240516367141460862187749451047644094885791761673574674330840842792189795049968394122216854491757922647656430908587059997070488674220330847871811836724541907666983042376216411561826640060734307013458794925025684062804589439843027290282034999617915124231838524593607080377300985152179828199569474241678651559771763395596697140206072537688129790126472053987391538280007082203006348029125729650207661362371936196789562658458778312533505938858959644541233578654340925901963957980047639114170033936570060250438906130591377904182111622236567507022711176457301476543461600524993045300728432815672077399879668276471832

phi = (Q-1)*(p-1)
d = gmpy2.invert(base,phi)
m = pow(Ciphertext,d,Q*p)
print(long_to_bytes(m))
b'MRCTF{sti11_@_b@by_qu3st10n}'

[MRCTF2020]Easy_RSA

import sympy
from gmpy2 import gcd, invert
from random import randint
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger, bytes_to_long, long_to_bytes
import base64

from zlib import *
flag = b"MRCTF{XXXX}"
base = 65537

def gen_prime(N):
    A = 0
    while 1:
        A = getPrime(N)
        if A % 8 == 5:
            break
    return A

def gen_p():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("P_n = ", n)
    F_n = (p - 1) * (q - 1)
    print("P_F_n = ", F_n)
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


def gen_q():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("Q_n = ", n)
    e = getRandomNBitInteger(53)
    F_n = (p - 1) * (q - 1)
    while gcd(e, F_n) != 1:
        e = getRandomNBitInteger(53)
    d = invert(e, F_n)
    print("Q_E_D = ", e * d)
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)


if __name__ == "__main__":
    _E = base
    _P = gen_p()
    _Q = gen_q()
    assert (gcd(_E, (_P - 1) * (_Q - 1)) == 1)
    _M = bytes_to_long(flag)
    _C = pow(_M, _E, _P * _Q)
    print("Ciphertext = ", _C)
'''
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201

Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
'''

解码：

需要先求出P和Q，看加密的自定义函数 gen_p 和 gen_q

gen_p：

def gen_p():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("P_n = ", n) 得知 P_n => P_p * P*q
    F_n = (p - 1) * (q - 1)
    print("P_F_n = ", F_n) 得知 P_F_n => (P_p-1)*(P*q-1)
    factor2 = 2021 * p + 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)

那么计算 P = factor2 = 2021 * p + 2020 * q

已知 P_p * P*q 和 (P_p-1)*(P*q-1)

可用解方程得

P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
p_q= P_n - P_F_n +1
P_p=(p_q-gmpy2.iroot(p_q*p_q-4*P_n,2)[0])//2
P_q= P_n // P_p
factor1 = 2021*P_p + 2020*P_qif factor1 < 0:
    factor1 = (-1) * factor1
P= sympy.nextprime(factor1)

gen_q：

def gen_q():
    p = getPrime(1024)
    q = getPrime(1024)
    assert (p < q)
    n = p * q
    print("Q_n = ", n)
    e = getRandomNBitInteger(53)
    F_n = (p - 1) * (q - 1)
    while gcd(e, F_n) != 1:
        e = getRandomNBitInteger(53)
    d = invert(e, F_n)
    print("Q_E_D = ", e * d)
    factor2 = 2021 * p - 2020 * q
    if factor2 < 0:
        factor2 = (-1) * factor2
    return sympy.nextprime(factor2)

Q_n 可以直接分解

Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Q_p = 120538849514661970159855851547577637711900368732462953774738483480759950867244867240401273864984981385806453735655967797329769252143125966966236767391995563418243748302685348336642872306042286401427581501609713577329945760930395130411743322595026287853073310150103535873078436896035943385067893062698858976291
Q_q = 171847486694659608706336923173786708071603689972942289760669690002615525263534483261477699540482615520223300780778172120221008417518590133753701145591943840552802072474293556608389677806415392384924913911677288126066245025731416399656855625839288752326267741979436855441260177305707529456715625062080892327017
factor2 = 2021 * Q_p - 2020 * Q_q
if factor2 < 0:
    factor2 = (-1) * factor2
Q = sympy.nextprime(factor2)

得出P和Q后，按正常rsa解码：

import sympy
import gmpy2
from Crypto.Util.number import *
P_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024336556028267742021320891681762543660468484018686865891073110757394154024833552558863671537491089957038648328973790692356014778420333896705595252711514117478072828880198506187667924020260600124717243067420876363980538994101929437978668709128652587073901337310278665778299513763593234951137512120572797739181693
P_F_n =  14057332139537395701238463644827948204030576528558543283405966933509944444681257521108769303999679955371474546213196051386802936343092965202519504111238572269823072199039812208100301939365080328518578704076769147484922508482686658959347725753762078590928561862163337382463252361958145933210306431342748775024099427363967321110127562039879018616082926935567951378185280882426903064598376668106616694623540074057210432790309571018778281723710994930151635857933293394780142192586806292968028305922173313521186946635709194350912242693822450297748434301924950358561859804256788098033426537956252964976682327991427626735740
P_p = 118153578345562250550767057731385782963063734586321112579869747650001448473633860305142281504862521928246520876300707405515141444727550839066835195905927281903880307860942630322499106164191736174201506457157272220802515607939618476716593888428832962374494147723577980992661629254713116923690067827155668889571
P_q = 118975085954858660642562584152139261422493348532593400307960127317249511761542030451912561362687361053191375307180413931721355251895350936376781657674896801388806379750757264377396608174235075021854614328009897408824235800167369204203680938298803752964983358298299699273425596382268869237139724754214443556383
factor1 = 2021 * P_p + 2020 * P_q
if factor1 < 0:
    factor1 = (-1) * factor1
P = sympy.nextprime(factor1)
p_q= P_n - P_F_n +1
P_p=(p_q-gmpy2.iroot(p_q*p_q-4*P_n,2)[0])//2
P_q= P_n // P_p
factor1 = 2021*P_p + 2020*P_q
if factor1 < 0:
    factor1 = (-1) * factor1
P= sympy.nextprime(factor1)

Q_n =  20714298338160449749545360743688018842877274054540852096459485283936802341271363766157976112525034004319938054034934880860956966585051684483662535780621673316774842614701726445870630109196016676725183412879870463432277629916669130494040403733295593655306104176367902352484367520262917943100467697540593925707162162616635533550262718808746254599456286578409187895171015796991910123804529825519519278388910483133813330902530160448972926096083990208243274548561238253002789474920730760001104048093295680593033327818821255300893423412192265814418546134015557579236219461780344469127987669565138930308525189944897421753947
Q_E_D =  100772079222298134586116156850742817855408127716962891929259868746672572602333918958075582671752493618259518286336122772703330183037221105058298653490794337885098499073583821832532798309513538383175233429533467348390389323225198805294950484802068148590902907221150968539067980432831310376368202773212266320112670699737501054831646286585142281419237572222713975646843555024731855688573834108711874406149540078253774349708158063055754932812675786123700768288048445326199880983717504538825498103789304873682191053050366806825802602658674268440844577955499368404019114913934477160428428662847012289516655310680119638600315228284298935201
Q_p = 120538849514661970159855851547577637711900368732462953774738483480759950867244867240401273864984981385806453735655967797329769252143125966966236767391995563418243748302685348336642872306042286401427581501609713577329945760930395130411743322595026287853073310150103535873078436896035943385067893062698858976291
Q_q = 171847486694659608706336923173786708071603689972942289760669690002615525263534483261477699540482615520223300780778172120221008417518590133753701145591943840552802072474293556608389677806415392384924913911677288126066245025731416399656855625839288752326267741979436855441260177305707529456715625062080892327017
factor2 = 2021 * Q_p - 2020 * Q_q
if factor2 < 0:
    factor2 = (-1) * factor2
Q = sympy.nextprime(factor2)

Ciphertext =  40855937355228438525361161524441274634175356845950884889338630813182607485910094677909779126550263304194796000904384775495000943424070396334435810126536165332565417336797036611773382728344687175253081047586602838685027428292621557914514629024324794275772522013126464926990620140406412999485728750385876868115091735425577555027394033416643032644774339644654011686716639760512353355719065795222201167219831780961308225780478482467294410828543488412258764446494815238766185728454416691898859462532083437213793104823759147317613637881419787581920745151430394526712790608442960106537539121880514269830696341737507717448946962021
base = 65537

phi = (Q-1)*(P-1)
d = gmpy2.invert(base,phi)
m = pow(Ciphertext,d,P*Q)
print(long_to_bytes(m))

#b'MRCTF{Ju3t_@_31mp13_que3t10n}'

posted @ 2024-01-18 20:01 Nineday_九日之景阅读(1036) 评论(2) 收藏举报

刷新页面返回顶部

Ninedayneverlostroad

BUUCTF—Crypto（完结版本—_—）

BUUCTF—Crypto

1.一眼就解密

2.MD5

3.URL编码

4.看我回旋踢

5.摩丝

6.passwork

7.Quoted-ptintable

8.Rabbit

9.篱笆墙的影子

10.RSA

11.Alice与Bob

12.大帝的密码武器

13.rasrsa

14.萌萌哒的八戒

15.old-fashion

16.Unencode

17.[AFCTF2018]Morse

18.变异凯撒

19.丢失的MD5

20.Windows系统密码

21.信息化时代的步伐

22.凯撒？替换？呵呵！

23.权限获得第一步

24.传统知识+古典密码

25.RSA1

26.世上无难事

27.RSA2

28.RSA3

29.还原大师

30.异性相吸

31.RSAROLL

32.RSA

[MRCTF2020]babyRSA

[MRCTF2020]Easy_RSA

公告