单调队列优化

Rudolf and k Bridges

题面翻译

有一条 \(n \times m\) 的河。第 \(i\) 行第 \(j\) 列的深度为 \(a_{i, j}\)。保证 \(a_{i, 1} = a_{i, m} = 0\)。

如果在第 \(i\) 行第 \(j\) 列安置桥墩，所需代价为 \(a_{i, j} + 1\)。

你需要选择连续的 \(k\) 行，每行都要架起若干个桥墩，并满足以下条件：

1. 每行的第 \(1\) 列必须架桥墩；
2. 每行的第 \(m\) 列必须架桥墩；
3. 每行的相邻两个桥墩的距离不超过 \(d\)。其中 \((i, j_1)\) 和 \((i, j_2)\) 之间的距离为 \(|j_1 - j_2| - 1\)。

求最小代价和。

样例 #1

样例输入 #1

5
3 11 1 4
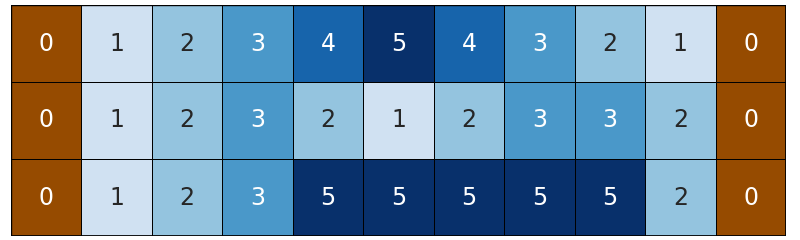
0 1 2 3 4 5 4 3 2 1 0
0 1 2 3 2 1 2 3 3 2 0
0 1 2 3 5 5 5 5 5 2 0
4 4 2 1
0 3 3 0
0 2 1 0
0 1 2 0
0 3 3 0
4 5 2 5
0 1 1 1 0
0 2 2 2 0
0 2 1 1 0
0 3 2 1 0
1 8 1 1
0 10 4 8 4 4 2 0
4 5 3 2
0 8 4 4 0
0 3 4 8 0
0 8 1 10 0
0 10 1 5 0

样例输出 #1

4
8
4
15
14

提示

思路

我们可以创建动态规划，\(dp[i][j]\)为每个点的最小花费，显而易见的状态转移为\(dp[i][j-d]\)的范围到\(dp[i][j-1]\)的最小花费加\(g[i][j]\)的花费

那我们怎么样找\(dp[i][j-d]\)的范围到\(dp[i][j-1]\)的最小花费呢，可以一个个枚举，但是太麻烦了，我们可以考虑用单调队列优化，记录队列中可使用的最小花费，每次把最优取出即可

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t, n, m, k, d;
    cin >> t;
    while (t--) {
        cin >> n >> m >> k >> d;
        // 使用 vector 定义二维数组
        vector<vector<long long>> g(n + 1, vector<long long>(m + 1));
        vector<vector<long long>> dp(n + 1, vector<long long>(m + 1,0x3f3f3f3f));
        // 输入二维数组 g
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                cin >> g[i][j];
            }
        }
        // 动态规划
        for (int i = 1; i <= n; i++) {
            dp[i][1] = 1;
            //初始一定放桥
        }
        for (int i = 1; i <= n; i++) {
            deque<int> q;
            q.push_back(1);
            for (int j = 2; j <= m; j++) {
            	//更少花费且后进来的，后结束又优，前进来的没有价值了
                while(q.size()>0&&dp[i][q.back()]>dp[i][j-1]) q.pop_back();
                q.push_back(j-1);
                //花费少但是过期了也要删掉
                while(q.size()>0&&q.front()<j-d-1) q.pop_front();
                //最优加当前花费
                dp[i][j] = dp[i][q.front()]+g[i][j]+1;
            }
        }
        int l=1,r=1,co=0;
        long long res = 1e12,tmp=0;
        //滑动窗口找连续k个
        while(r<=n){
        	if(dp[r][m]!=0x3f3f3f3f){
        		tmp += dp[r][m];
        		co++;
        		r++;
        	}
        	else{
        		tmp = 0;
        		k = 0;
        		r++;
        		l = r;
        		co = 0;
        	}
        	if(co==k){
        		res = min(res,tmp);
        		tmp -= dp[l][m];
        		l++;
        		co--;
        	}
        }
        cout << res << endl;
    }

    return 0;
}