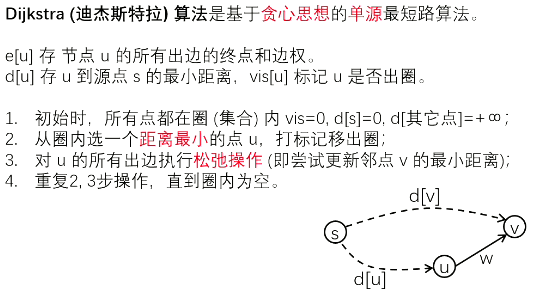
单源最短路 Dijkstra

单源最短路

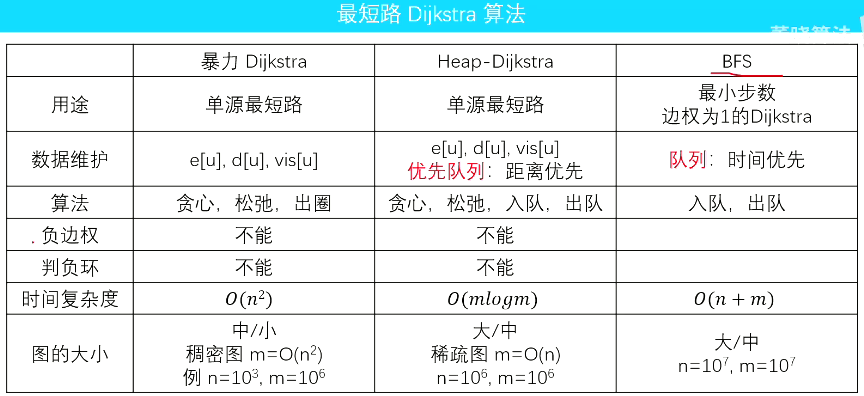
朴素做法

//dijkstra算法 单源最短路
//思路 d[u]存点u到原点s的最小距离，vis[u]记录是否走过 
//1.初始化 2.选一个距原点s最小的点 3.将该点相邻点改写最短距离 

struct edge{
	int v,w;
};

const int N = 1005;
vector <edge> g[N];
int vis[N]={},d[N],n,m;

//时间复杂度 n^2+m	空间复杂度 m
void dijkstra(int s){
	//初始化 所有点到原点的距离 d 所有点未被标记 
	memset(d,0x3f,sizeof(d));
	//原点到自己距离为 0 
	d[s] = 0;
	for(int i=1;i<n;i++){
		int u = 0;
		//注意u为 0不为 1,0相当于哨兵节点,其他点可能被标记 
		for(int j=1;j<=n;j++){
			if(!vis[j]&&d[u]>d[j])
				u = j;
			//找距离最近且没标记的点 
		}
		for(auto a:g[u]){
			if(d[u]+a.w<d[a.v]){
				d[a.v] = d[u]+a.w;
			}
 		}
 		vis[u] = 1;
	}
}

堆优化

//堆优化dijkstra 单源最短路 
//贪心策略 找到离原点最近距离的点 更新邻点重复
//代码实现 优先队列存节点和距原点距离 vis记录是否走过点数组  

struct edge{
	int v,w;
};
//存点相邻边

struct node{
	int d,l;
	friend bool operator<(node n1,node n2){
		//注意希望顶元素为小，所以排序从大到小 
		n1.l > n2.l;
	}
};
//存节点给大根堆 
const int N = 1005;
int vis[N]={},d[N],n,m,s;
priority_queue <node> pq; 
vector <edge> g[N];
//时间复杂度 mlognm 空间复杂度 m
void dijkstra(){
	pq.push({s,0});
	memset(d,0x3f,sizeof(d));
	d[s] = 0;
	while(!pq.empty()){
		auto nd = pq.top();
		cout << nd.d << " " << nd.l << endl;
		pq.pop();
		//队列可能有多个同节点，不过没有关系
		//顶元素最小 
		if(vis[nd.d]==1) continue;
		for(auto a:g[nd.d]){
			int le = a.w+nd.l;
			d[a.v] = min(d[a.v],le);
			pq.push({a.v,le});
		}
		vis[nd.d] = 1;
	}
}

搜索路径

//dijkstra算法 单源最短路
//思路 d[u]存点u到原点s的最小距离，vis[u]记录是否走过 
//1.初始化 2.选一个距原点s最小的点 3.将该点相邻点改写最短距离 
struct edge{
	int v,w;
};

const int N = 1005;
vector <edge> g[N];
int vis[N]={},d[N],n,m,pre[N];

//时间复杂度 n^2+m	空间复杂度 m
void dijkstra(int s){
	//初始化 所有点到原点的距离 d 所有点未被标记 
    memset(d,0x3f,sizeof(d));
	//原点到自己距离为 0 
	d[s] = 0;
	for(int i=1;i<n;i++){
		int u = 0;
		//注意u为 0不为 1,0相当于哨兵节点,其他点可能被标记 
		for(int j=1;j<=n;j++){
			if(!vis[j]&&d[u]>d[j])
				u = j;
			//找距离最近且没标记的点 
		}
		for(auto a:g[u]){
			if(d[u]+a.w<d[a.v]){
				d[a.v] = d[u]+a.w;
				//记录上一点 
				pre[a.v] = u;
			}
 		}
 		vis[u] = 1;
	}
}

//搜索路径
void dfs(int x,int s){
	if(x==s){
		cout << x << " ";
		return;
	}
	dfs(pre[x],s);
	cout << x << " ";
}