平衡二叉搜索树

PART 0：引子

二叉树想必大家都很熟悉，它在编程中具有很广泛的应用，而二叉树又分为很多种，这里介绍的了两种二叉树和一种他们的结合体。

PART 1：二叉搜索树

二叉搜索树的定义

二叉搜索树要求任意一个节点的左子节点小于它，右子节点大于它。

如图

在二叉搜索树上查找的时间复杂度相比线性结构一般要快一些，但是它有可能退化为链表，那样的话就和线性结构并无二致了。当然，这不是我们在这里要解决的问题。

二叉搜索树的查找

由于二叉搜索树的节点有一定顺序，查找起来其实非常方便，可以用递归实现：

//这里用的是int类型，运用时根据实际需求可以改变
int find(Node x,int key){
    //在以x为根结点的子树中查找并返回键key所对应的值
    //如果找不到，就返回null
    if(x==null) return null;
    if(key<x.key) return find(x.left,key);
    else if(key>x.left) return find(x.right,key);
    else return x.value;
}

下面用一个动图给大家演示一下在这个二叉搜索树里查找32的过程

最大值与最小值

根据二叉搜索树的定义，最大值就是最右端的节点，而最小值就是最左端的节点，只需要从根节点一直往右或往左走就行了。

二叉搜索树的插入

插入和查找其实很相似，只需要在树上查找要插入的元素的值，如果树上已经有了该元素，则不必插入，如果没有，那么终止的位置就是要插入的位置

Node insert(Node x,int key,int value){
    //如果key存在于以x为根节点的子树中则更新它的值；
    //如果不在就创建新节点插入到合适的位置；
    if(x==null) return new Node(key,value);
    if(key<x.key) x.left=insert(x.left,key,value);
    else if(key>x.key) x.right=insert(x.right,key,value);
    else x.value=value;
    return x;
}

如图：

二叉搜索树的删除

删除分为三种情况：

1. 要删除的节点没有子节点

直接删，不用管。

如图，我们要删除 \(27\)

2. 要删除的节点只有一个子节点

将它父亲指向它的指针修改为指向它的子节点，然后删除它。

如图，我们要删除 \(50\)

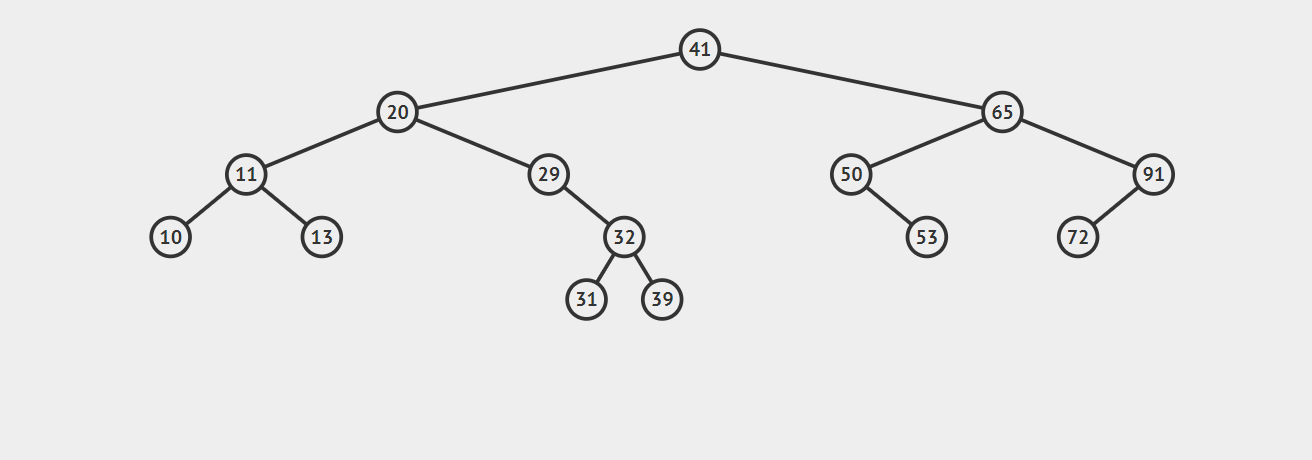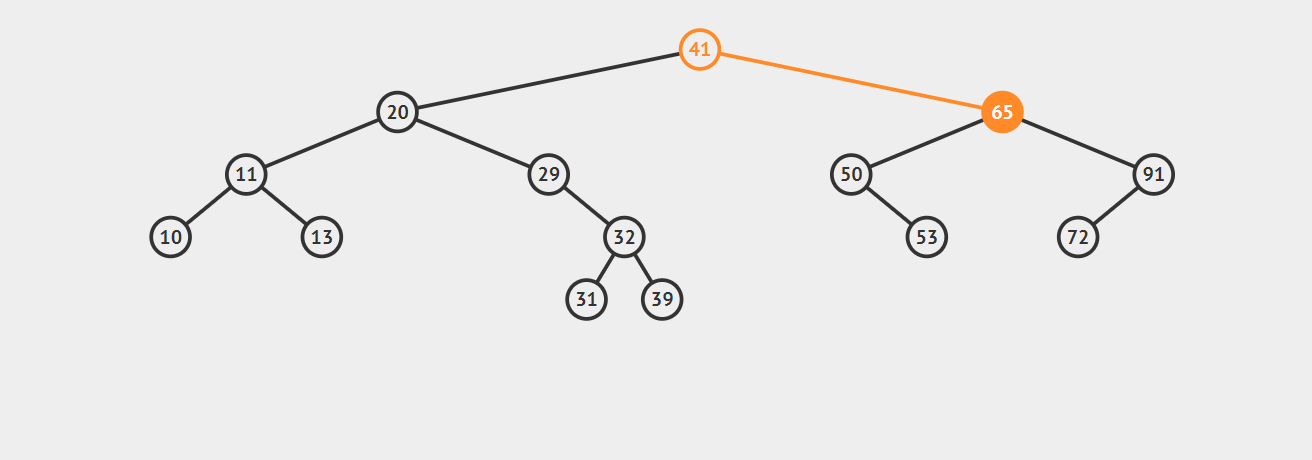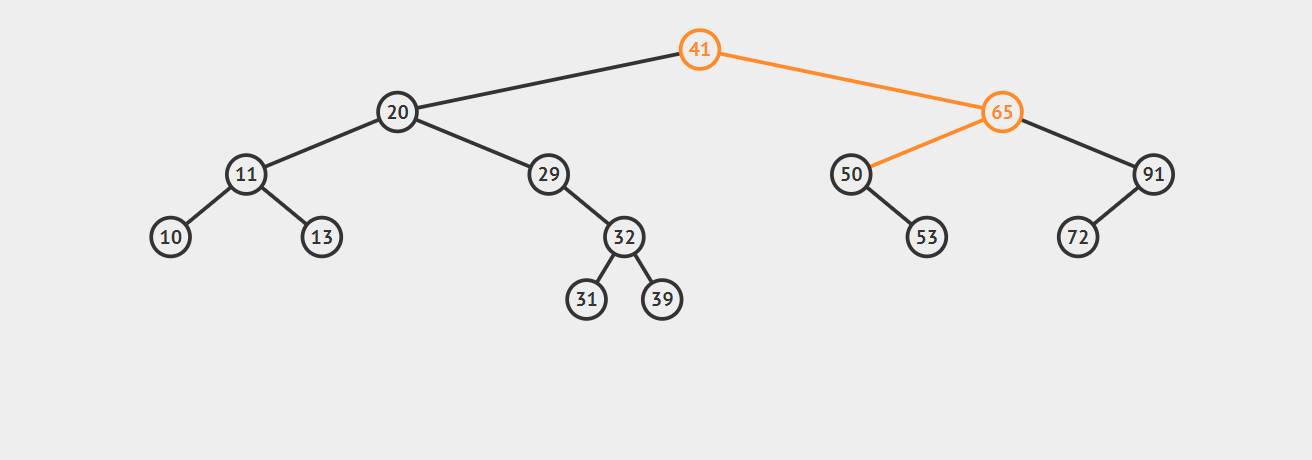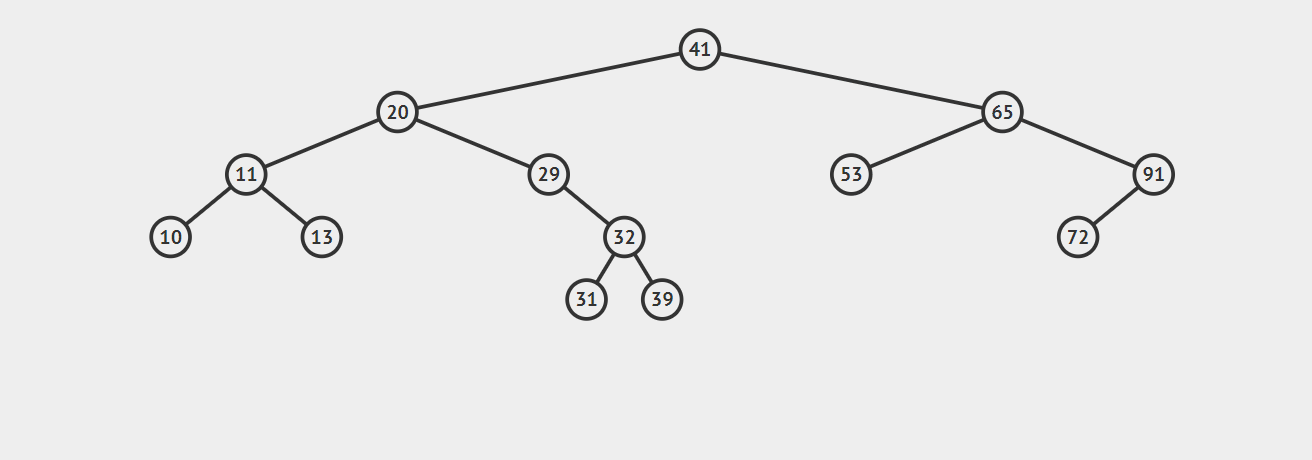
3. 要删除的节点有多个子节点

这是最麻烦的一种情况，有两种做法，取它左子树上最大的点或右子树上最小的点来代替它。

如图，我们要删除节点 \(20\)，这里取的是右子树上最小的点

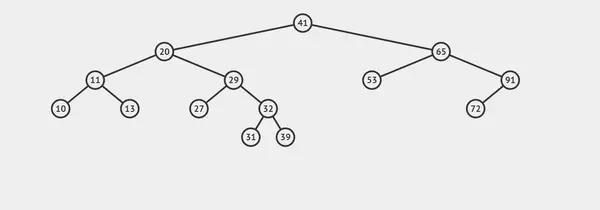
PART 2：平衡二叉树

平衡二叉树的定义

平衡二叉树要求任意一个节点的左子树和右子树的高度差小于等于 \(1\)，当然，也可以是空树

如图，这就是一个平衡二叉树

平衡因子

在上图中，我们在每一个节点上都标记了一个数字，这就是平衡二叉树的平衡因子。

平衡因子就是是某节点的左子树和右子树的高度差。在平衡二叉树中，平衡因子只能为 \(0,1,-1\) 这三者之一，否则就不满足平衡二叉树的定义。

如图，下面是平衡因子的三种情况的图示

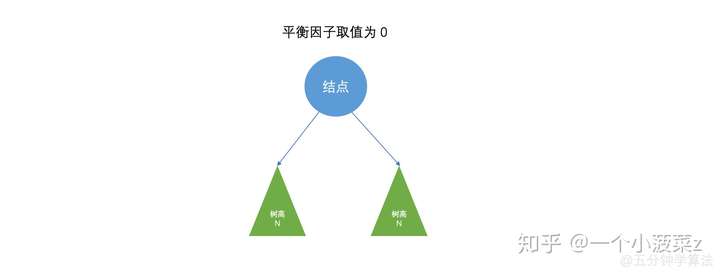
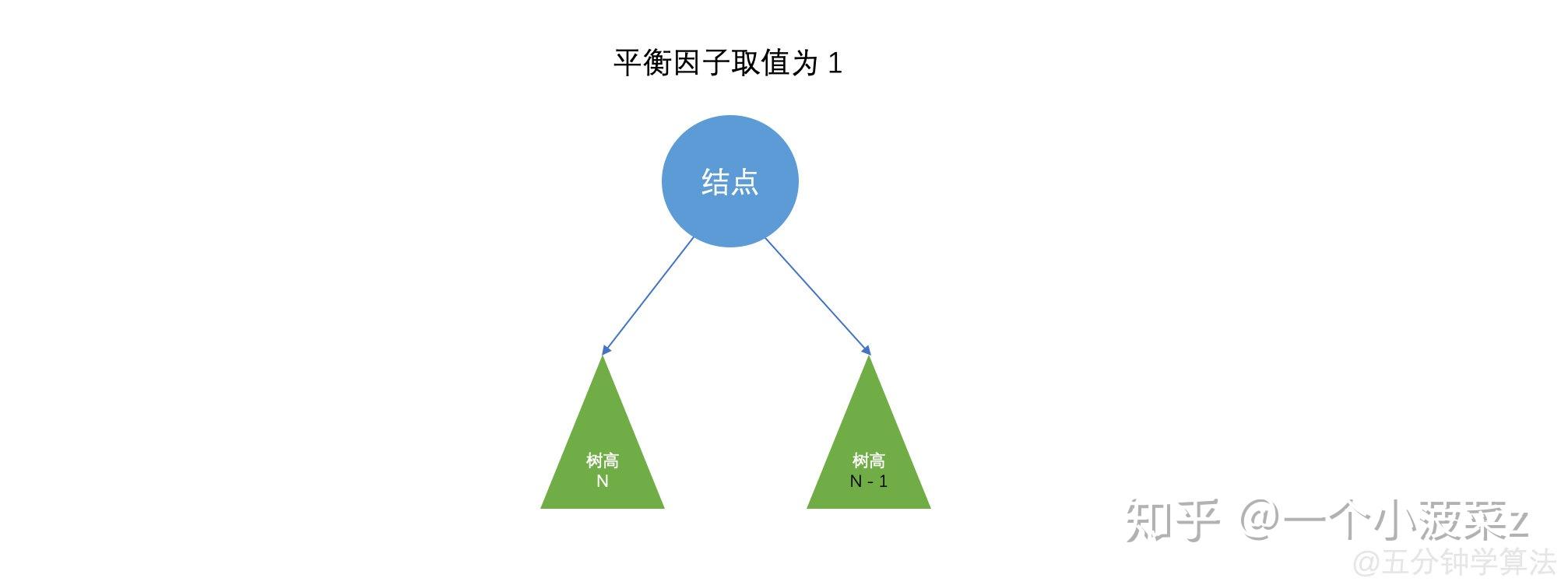
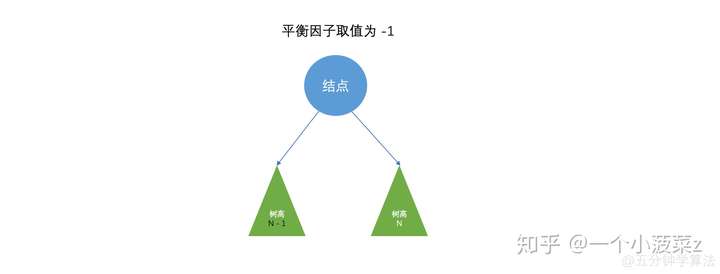
平衡二叉树的调整

上面介绍了平衡二叉树，那么如果一颗二叉树不是平衡二叉树，我们应该怎么将其调整为平衡二叉树呢？

这里有四种调整情方法，对应四种不合法的情况：

左单旋(RR)

如图，这是一颗平衡二叉树

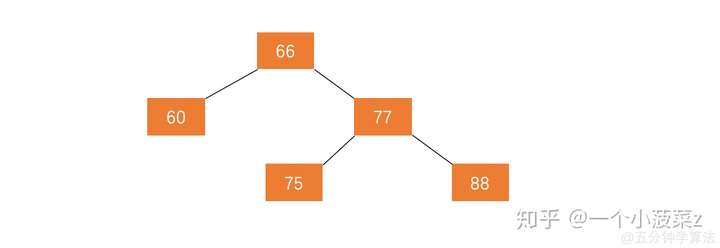
在这棵树上插入节点99，得到的树如下所示

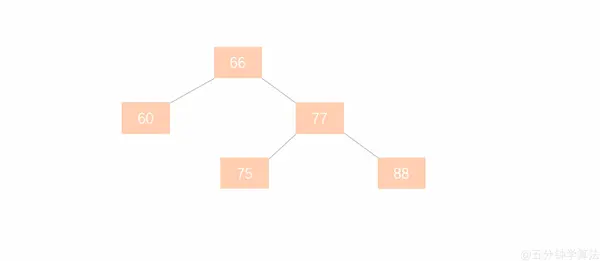
这样的话，这棵树就失去了平衡，因此我们要将他调整为一颗平衡树，
由于右子树高于左子树，所以我们将这颗树逆时针旋转，流程如下：

1. 节点的右子节点替代此节点位置

2. 右子节点的左子树变为该节点的右子树

3. 节点本身变为右子节点的左子树

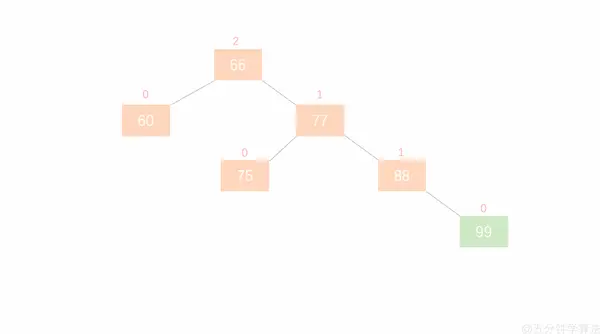
这样，这棵树就又恢复了平衡。

这种情况是在节点的右子节点的右侧插入节点，因此又称为 RR。

右单旋(LL)

右单旋的情况与左单旋类似，操作流程如下：

1. 节点的左子节点代表此节点

2. 节点的左子节点的右子树变为节点的左子树

3. 将此节点作为子节点节点的右子树。

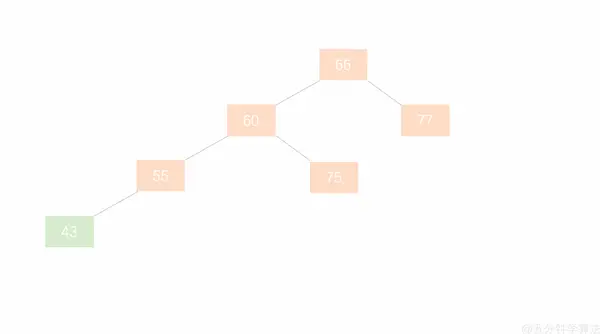
这种情况是在节点的左子节点的左侧插入节点，因此又称为 LL。

先左旋，再右旋（LR）

若 \(A\) 的左孩子节点 \(B\) 的右子树 \(E\) 插入节点 \(F\)，导致节点 \(A\) 失衡，如图：

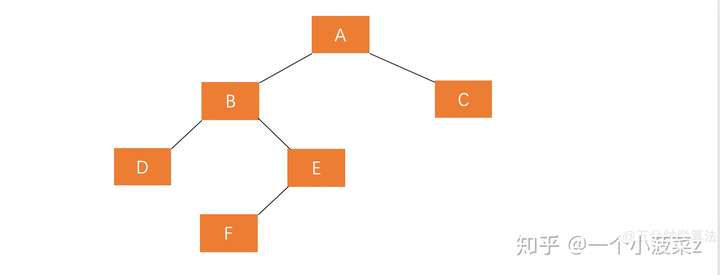
这个时候，仅仅一次旋转无法将其转化为平衡树，需要两步操作：

1. 对失衡节点 \(A\) 的左子节点 \(B\) 进行左旋

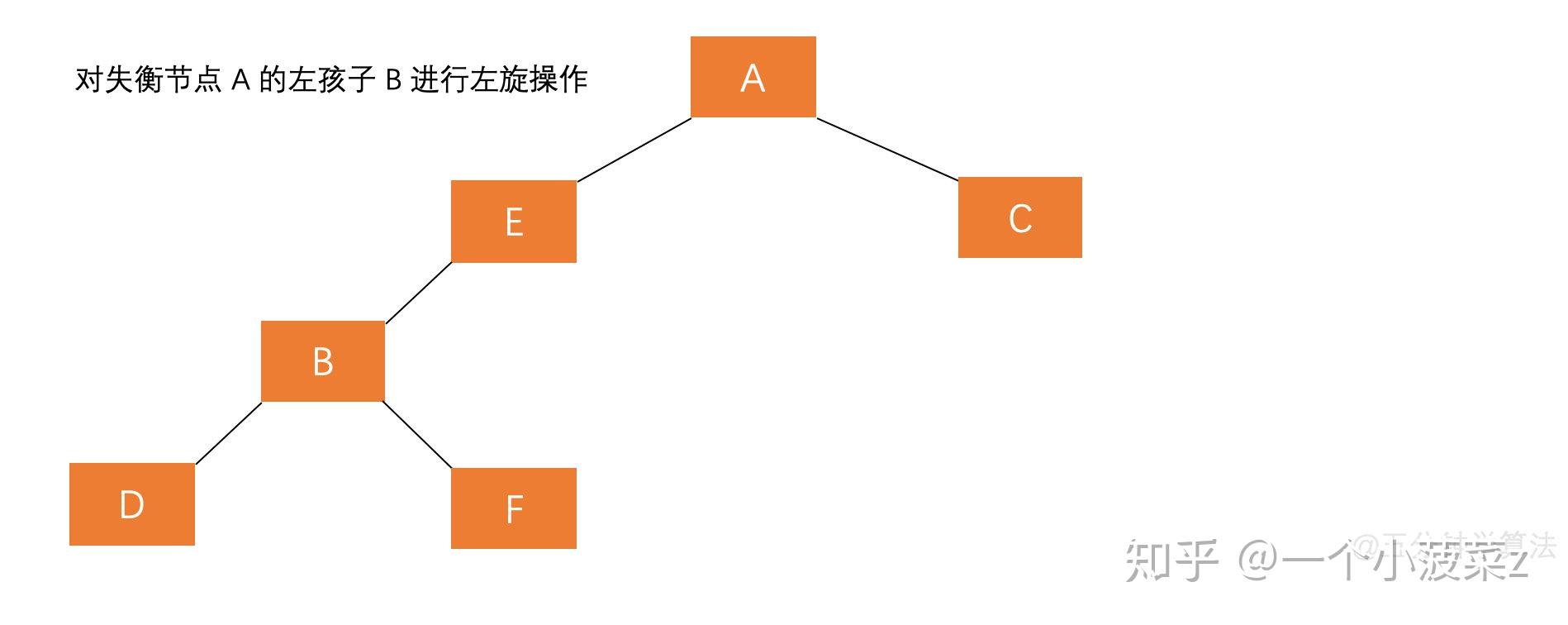
2. 对失衡节点 \(A\) 进行右旋

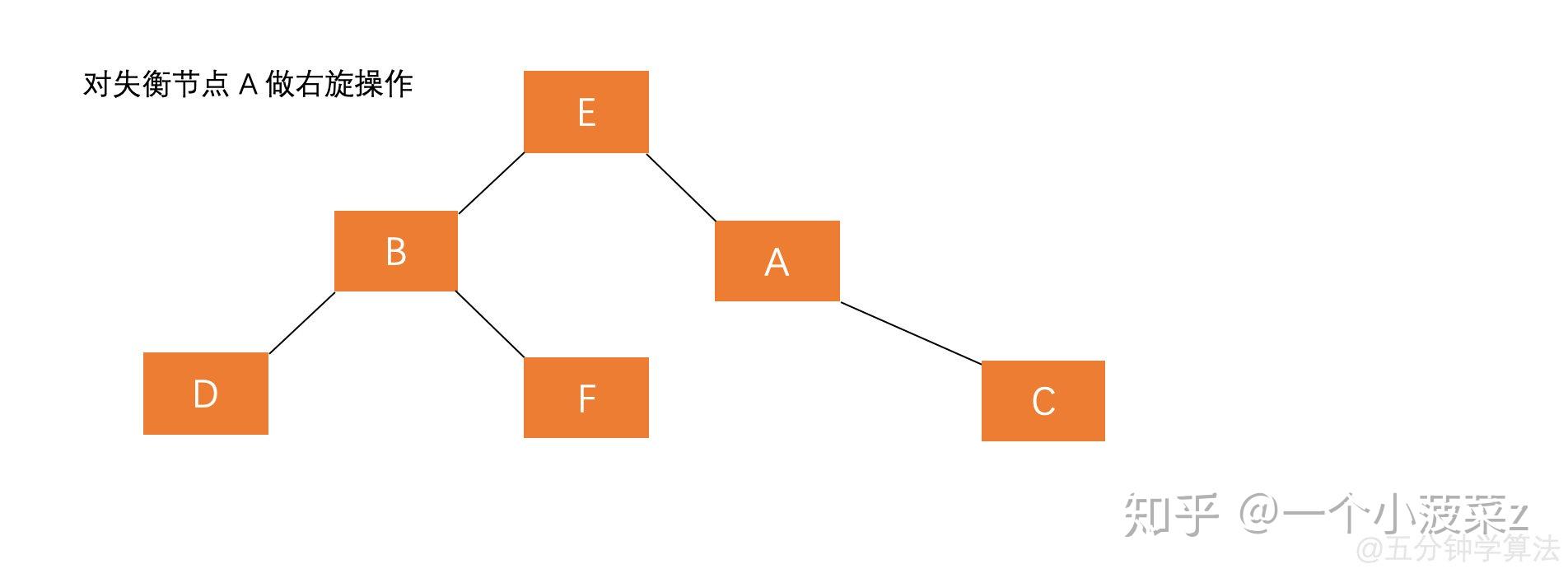
经过这两步操作，使得树恢复了平衡，同时原来根节点的左子节点的右子节点 \(E\) 成为了新的根节点。

先右旋，再左旋（RL）

与上面类似，在右子节点的左子树上插入节点也需要两部操作：

1. 对失衡节点 \(A\) 的右子节点 \(C\) 进行右旋

2. 对失衡节点 \(A\) 进行左旋

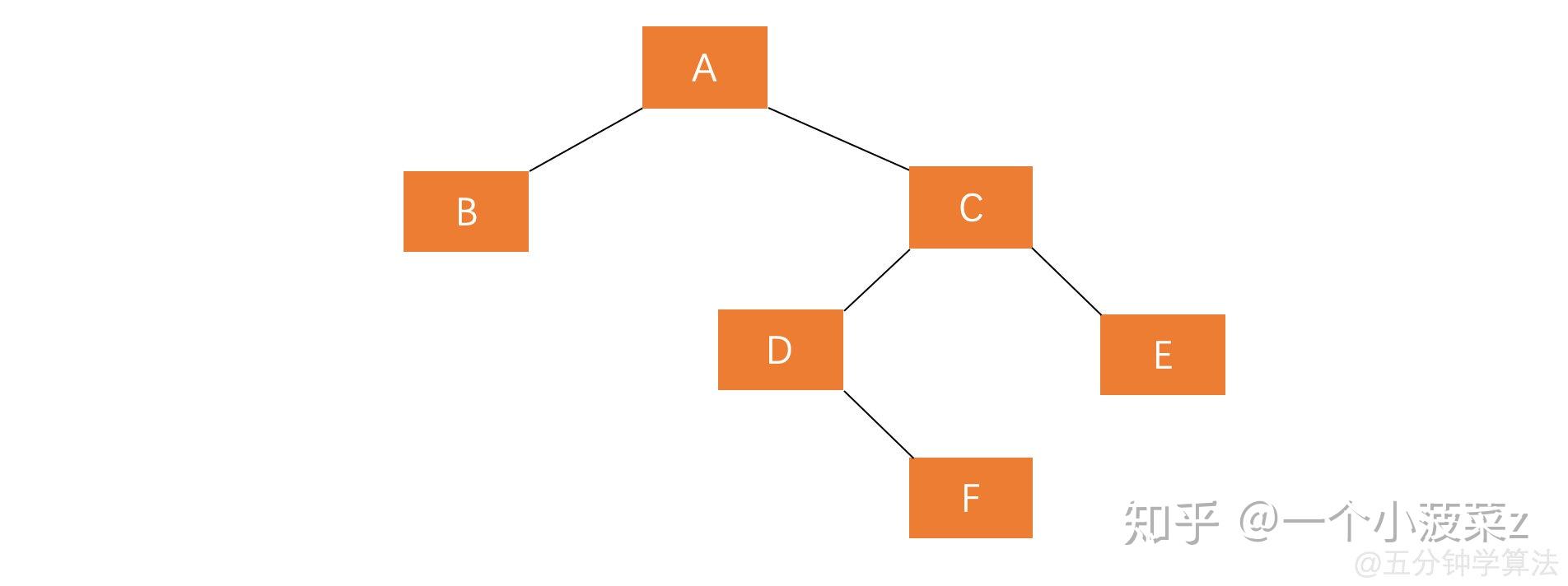
经过这两步操作，使得树恢复了平衡，同时原来根节点的右子节点左子节点 \(D\) 成为了新的根节点。

PART 3：二叉搜索平衡树

还记得上文中提到的二叉搜索树退化的事吗，退化成链后，二叉树相比于线性结构就没有任何的优势了，这个时候就要推出我们的二叉搜索平衡树。什么意思呢，就是使二叉搜索树满足平衡树的条件，这样的话可以防止它的退化，一旦有退化的趋势，就可以通过旋转将其再次变为平衡树。实际上，在平衡树的状态下，二叉搜索树的时间复杂度应该是最优的，是 \(O(\log n)\)。

对于平衡二叉树的操作，其实在上面两个部分已经分开讲完了，这里不再赘述。