UVA11504 Dominos 题解

PART 1：题目描述

题目是给出 \(n\) 块多米诺骨牌的关系，a b 表示 a 号骨牌能够推到 b 号骨牌。要求的是最少推几次才能够推到。

考虑把题意转化建模：给出一个 \(n\) 个点的有向图，a b 表示有一条从 a 到 b 的边，求最少从几个点开始遍历才能够覆盖整个图。

PART 2：解题思路

简化模型

先不考虑一般的图，考虑一个最简单的 DAG。你会用什么方法做？

并查集行吗？

本人一开始想到的是这种方法，用并查集维护关系，最后统计总共有几个并查集。如果是双向边的话，这种方法确实可行，但是由于是有向图，需要考虑方向的问题，所以需要在并查集中维护节点之间的父子关系，显然麻烦了，而且最后建出来的并查集就是原来的图，相当于是做无用功

怎么做？

想一想，加入在一个无向图中，我们怎么统计并查集的思路，一般来说可以枚举每个节点看有哪些节点的父节点还是初始值，也就没有父节点。换到有向图中，同样是这个想法。在有向图中，没有父节点的点就是入度为 \(0\) 的点，所以我们只要统计 DAG 中每个点的入度就可以了，而答案就是入度为 \(0\) 的点的数量。其实按照题目意思也可以想到，我们求的是最少从几个点开始遍历才能够覆盖整个图。而入度为 \(0\) 的点显然不可能从别的点开始遍历然后遍历到。

难度加大

刚刚是对于 DAG 的情况，现在我们考虑一般的图。

一般的图可就没有 DAG 那么友好了，它是有环的。如果你对它的恶意没有体会的话，你可以试着构造一个简单的图，比如整张图只有一个环，那么我们上面得到的结论就显然不成立了。

怎么办？

考虑怎么把一张一般的图变成 DAG

看下面的一张图片

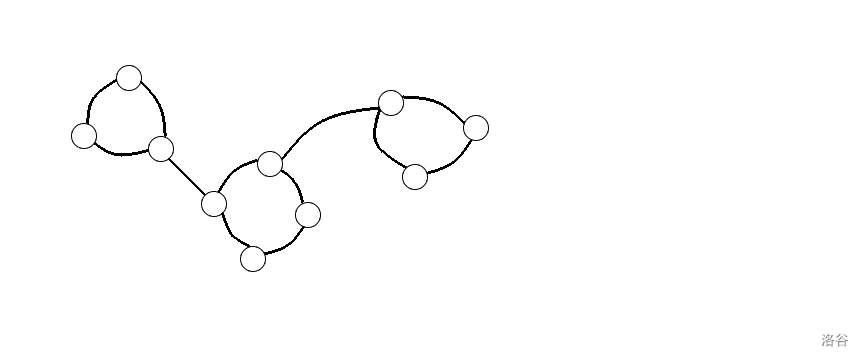
它的答案显然是二，那它会让你想到一张怎样的 DAG 图呢？

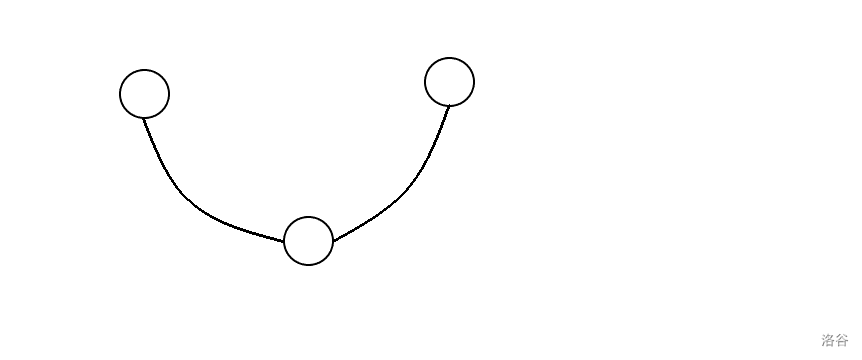
想必是这张。这两张图答案是一样的，实际上性质也很类似。那么下面的图是怎么变过来的呢？你可能会说是把环变成一个点，但实际上，不仅仅是环，只要是一个强连通分量都可以缩成一个点。而强连通分量缩点是可以用 tarjan 算法简单完成的。

PART 3：AC 代码

代码很简单，但注意多组数据。

#include<bits/stdc++.h>
#define MAXN 100010
#define MAXM 100010
using namespace std;
struct edge{
    int pre,to;
};
edge e[MAXM];
stack<int> s;
int t, n, m, cnt, tot, times;
int head[MAXN], dfn[MAXN], low[MAXN], col[MAXN], deg[MAXN];
bool vis[MAXN];
void add_edge(int u, int v){
    e[++cnt].pre = head[u];
    e[cnt].to = v;
    head[u] = cnt;
}
void tarjan(int now){
    dfn[now] = low[now] = ++times;
    vis[now] = true; s.push(now);
    for(int i = head[now]; i; i = e[i].pre){
        if(!dfn[e[i].to]){
            tarjan(e[i].to);
            low[now] = min(low[now], low[e[i].to]);
        }else if(vis[e[i].to]){
            low[now] = min(low[now], low[e[i].to]);
        }
    }
    if(low[now] == dfn[now]){
        col[now] = ++tot; vis[now] = false;
        while(!s.empty() && s.top() != now){
            int p = s.top(); s.pop();
            col[p] = tot; vis[p] = false;
        }
        s.pop();
    }
}
int main(){
    scanf("%d",&t);
    while(t--){
        memset(dfn, 0, sizeof(dfn));
        memset(low, 0, sizeof(low));
        memset(vis, 0, sizeof(vis));
        memset(col, 0, sizeof(col));
        memset(deg, 0, sizeof(deg));
        memset(head, 0, sizeof(head));
        tot = 0; cnt = 0; times = 0;
        scanf("%d%d",&n,&m);
        for(int i = 1; i <= m; i++){
            int u, v;
            scanf("%d%d",&u,&v);
            add_edge(u, v);   
        }
        for(int i = 1; i <= n; i++){
            if(!dfn[i]) tarjan(i);
        }
        for(int p = 1; p <= n; p++){
            for(int i = head[p]; i; i = e[i].pre){
                if(col[p] != col[e[i].to]){
                    deg[col[e[i].to]]++;
                }
            }
        }
        int ans = 0;
        for(int i = 1; i <= tot; i++) if(deg[i] == 0) ans++;
        printf("%d\n",ans);
    }
    return 0;
}