最通俗易懂的计算机底层教学,二进制到汇编学习
汇编语言
汇编语言-编译器--》0100000(机器语言)
汇编一般用于底层的编写,单片机
进制
1进制:一进一,结绳记事。11
2进制:二进一,计算机
八进制:八进一。8个符号组成:01234567
10进制:10进-。10个符号组成:0123456789
16进制:16进-。16个符号组成:0123456789abcdef

狂神的十进制:02478abrdf,可以自己随便定义的,学习,创造者!
加密解密:程序员,破解程序的人!进制的加密(自己定义进制)
数字量一大,总是有规律的!
进制的运算
八进制计算下面结果
2+3=5(2后面往3位)
23=6(3个2)
4+5=11
45=24
运算的本质就是查数
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 20 21 22 23 24 25

277+333=632
276*54=20250
277
333
-----
632
276
54
----
1370
1666
----
20250
减法的本质其实就是加法
除法的本质 其实就是乘法,47*4,找到最接近234的数
234
4
47
结论:无论是什么进制,本身都有一套完美的运算体系,我们都可以通过列表将它计算出来
二进制和16进制的深层理解
计算机使用二进制0 1 状态:电子 物理极限:摩尔定律
追求语言的极限,并发操作,Go语言
量子计算机:使用量子计算的机器
传统计算机:集成电路0:1 硅晶片
量子计算机!提高计算机的计算力
示例:
二进制 1101 1010 → 十六进制 DA
1101 → D,1010 → A
二进制 0011 1110 → 十六进制 3E
(左侧补零后)0011 → 3,1110 → E
2. 十六进制 → 二进制
规则:将每位十六进制数直接展开为 4 位二进制数(按上表反向对应)。
示例:
十六进制 F5 → 二进制 1111 0101
F → 1111,5 → 0101
十六进制 A3 → 二进制 1010 0011
A → 1010,3 → 0011
- 为什么这种关系重要?
简化表达:
二进制数过长时(如 1101 1010 1111 0001),用十六进制表示为 DAF1,更易读写。
例如,内存地址、颜色代码(如 #FF0000 表示红色)均用十六进制简化二进制表达。
计算机底层兼容性:
计算机以二进制存储数据,但十六进制更便于人类理解和调试(如查看内存数据或机器码)。
快速转换:
无需通过十进制中转,直接按 4 位分组转换,效率极高。
- 应用场景
编程与调试:内存地址、寄存器值常用十六进制显示(如 0x1A3F)。
网络协议:MAC 地址(如 00:1A:2B:3C:4D:5E)使用十六进制。
文件编码:二进制文件内容常以十六进制形式查看(如 Hex 编辑器)。
总结
二进制和十六进制的关系本质是 4 位二进制 ⇄ 1 位十六进制,这种设计既保留了二进制在计算机中的底层逻辑,又通过十六进制提升了人类处理数据的效率。
忘记十进制的运算,不要将二进制转化为十进制来计算,而是直接用二进制来运算,这样才能学会汇编
为什么要学习理解二进制?
寄存器,内存,位,底层每一个位都是有含义的,汇编入门的基础!
汇编高级:了解程序的深层,操作系统的内核
数据宽度的理解
计算机:内存!给数据增加数据宽度
C和C++ JAVA都要定义数据类型,计算机底层需要我们给这些数据定义宽度
位 01
字节 0-0xFF(如果直接写 FF,编译器可能认为它是一个 变量名 或 字符串(如 "FF"),而非数值。加上 0x 后(如 0xFF),程序会明确知道这是一个 十六进制数。)
双字 0-0XFFFFFFF
在计算机中,每一个数据都需要给它定义数据类型,给它定义宽度,在内存中的宽度
有符号数和无符号数规则理解
无符号数规则
你这数字是什么,那就是什么
1001 1010 十六进制:0X9A 十进制154,一般都是二进制往十六进制转,不往十进制
有符号数规则
最高位是符号位:1(负数) 0(正数)
1001 1010 如何转换?原码反码补码
案例补充
为什么有符号的范围是-128-127,无符号的范围是0-255?
有符号和无符号整数的范围差异源于二进制位的分配方式不同,尤其是符号位的存在以及计算机用补码表示负数的方式。下面以 8位(1字节) 整数为例详细解释:
- 无符号整数(Unsigned)
所有8位均用于表示数值,没有符号位:
最小:0000 0000 ➔ 0
最大:1111 1111 ➔ 255
计算方式:2⁸ - 1 = 256 - 1 = 255
(所有位为1时,是从0到255共有256个可能值)
2. 有符号整数(Signed)
最高位(第8位)为符号位,剩下7位表示数值。
关键点:计算机用补码(Two's Complement) 表示负数,具体规则如下:
正数:符号位为 0,其余位直接表示数值(如 0010 1010 = 42)。
负数:符号位为 1,其他位通过取反后加1得到绝对值的二进制(如负数 -42 表示为 1101 0110)。
范围计算
最大正数:0111 1111 ➔ 127
(符号位为0,其他7位全1:2⁷ - 1 = 127)
最小负数:1000 0000 ➔ -128
原因:补码系统的特殊设计,1000 0000不表示-0,而是分配到-128,使得范围对称性被打破,但能多表示一个负数。
因此,有符号8位整数的范围是 -128 到 127(共256个数)。
原码反码补码
补充,帮助理解,现在计算机用补码表示负数
原码、反码和补码是计算机中用于表示有符号整数的三种编码方式。以下是它们的定义及示例说明:
1. 原码(Sign-Magnitude)
定义:最高位为符号位(0正1负),其余位表示数值的绝对值。
特点:
直观,但加减法需处理符号位,硬件实现复杂。
0有两种表示(+0和-0),如 00000000 和 10000000。
示例(8位):
+5:00000101
-5:10000101
2. 反码(Ones' Complement)
定义:
正数:与原码相同。
负数:符号位不变,其余位按位取反。
特点:
简化了减法,但仍有正负零问题。
示例(8位):
+5:00000101(与原码相同)
-5:
原码:10000101
反码:11111010
3. 补码(Two's Complement)
定义:
正数:与原码相同。
负数:反码加1。
特点:
统一加减法运算,消除正负零问题,硬件实现简单。
现代计算机普遍使用补码。
示例(8位):
+5:00000101(与原码相同)
-5:
原码:10000101
反码:11111010
补码:11111011
案例演示
场景1:计算 5 - 5
补码运算:
5 的补码:00000101
-5 的补码:11111011
相加:00000101 + 11111011 = 1 00000000(溢出后结果为 00000000,即 0)。
场景2:计算 3 + (-2)
补码运算:
3 的补码:00000011
-2 的补码:11111110
相加:00000011 + 11111110 = 1 00000001(溢出后结果为 00000001,即 1)。
关键区别总结
编码方式 正数表示 负数表示 0的表示 硬件实现
原码 符号位+绝对值 符号位+绝对值 +0和-0(两种) 复杂(需处理符号)
反码 与原码相同 符号位不变,其余位取反 +0和-0(两种) 较简单
补码 与原码相同 反码加1 唯一0(00000000) 最简单
补码的溢出处理
溢出规则:
若符号位进位(最高位溢出)且数值位无进位,结果为负数(如 -128 的补码 10000000)。
若符号位和数值位均进位,结果为正数(如 -1 + (-1) 补码运算:11111111 + 11111111 = 1 11111110,溢出后为 -2)。
总结
原码:直观但运算复杂,适合人类阅读。
反码:过渡方案,仍存在双零问题。
补码:计算机标准,高效统一加减法,彻底解决零的歧义。
编码规则
有符号数的编码规则
1、原码:最高位是符号位,对齐它的为本身绝对值
2、反码:
--正数:反码和原码相同
--负数:符号位一定是1,其余位对原码取反
3、补码:
--正数:反码和原码相同
--负数:符号位一定是1,反码+1
示例
1
原码 0000 0001
反码 0000 0001
补码 0000 0001
结论:如果是正数,原码、反码、补码都是一样的
-1
原码 1000 0001
反码 1111 1110
补码 1111 1111 就是1111 1110+1
-7
原码 1000 0111
反码 1111 1000
补码 1111 1001
看到一个数字,二进制的,需要了解它是有符号数还是无符号数
位运算理解-计算机的运算方法,不是我们理解的加减乘除
学习通过直接操作查看最有效,往寄存器存了-1,计算机显示FFFFFFFF 1111 1111...计算机是用补码进行存储
本质就是加减乘除
1就是接通,0就是没接通
与运算(and &)
计算机的本质
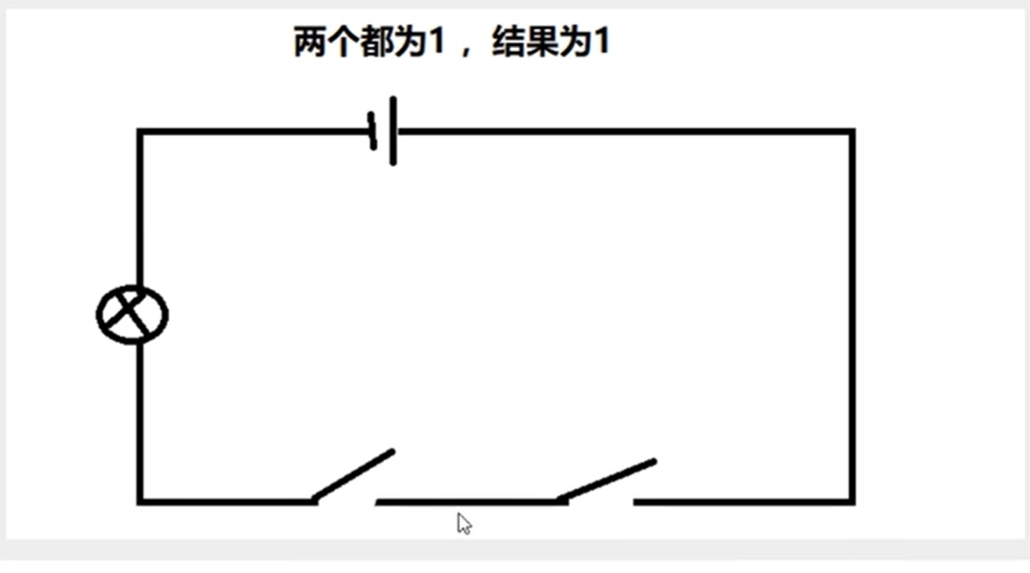
这个图的理解就是两个开关,只要其中一个开关接通了电路就能通
1011 0001
1101 1000
---------与运算,
1001 0000
或运算(or |)
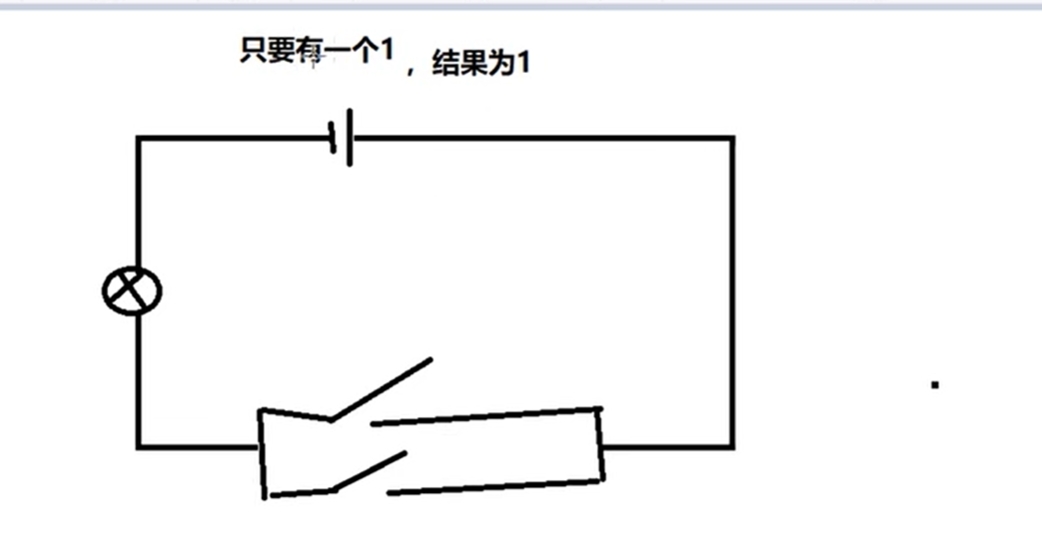
1011 0001
1101 1000
---------或运算,
1111 1001
异或运算(xor^)
不一样就是1 相同就是0

1011 0001
1101 1000
--
0110 1001
非运算(单目运算符 not~)
1110 0001
----
0001 1110
位运算(移动位,左移*2,右移除2)
左移*2 右移/2这只是相对于十进制而言
相对于计算机(纯二进制理解)
左移:(shl<<)
0000 0001 所有二进制位全部左移若干位,高位就丢弃了,低位补0
0000 0010
右移:(shr>>)
0000 0001 所有二进制位全部右移若干位,低位就丢弃了,高位补0,1(符号位决定)
0000 0010
0000 0001 1
0000 0010 2
0000 0100 4
0000 1000 8
位运算实现加减乘除
4+5=?
计算机是怎么操作的
0000 0100
0000 0101
---------加法(计算机是不会直接加的)
0000 1001(我们是会,直接加的)
计算机的实现原理

解释为什么会存在上面的步骤
第一步:如果不考虑进位的情况,异或运算和正常的加法是一样的结果
第二步:由于与运算不为0,所以肯定是存在进位1的情况,所以计算机会将与运算的结果向左移一位(就像正常的进位一样)
第三步:继续异或(就是相当于加法)
第四步:继续与运算判断,如果为0,那就是第三步异或后的结果了,如果不为0,那就继续进位,继续上面的流程
帮助理解位运算的链接
上面链接间帮助理解位运算的,这个案例有点抽象
汇编
在学习汇编之前,大家需要先掌握环境的配置 1、Vc6(程序到汇编的理解),2、OD!3、抓包工具、4、加密解密工具)前面两个工具是重点
C语言(应用)汇编(安全)二进制




 浙公网安备 33010602011771号
浙公网安备 33010602011771号