骗分论 2

排版 + 修改后的，~~虽然洛谷有很多人排版了~~（例如这里），不过窝还加了一些私货（
~~原作者是谁~~ /yiw

\[\textsf{骗分新论} \]

\[\mathbb{THE\;NEW\;GUIDE\;OF\;INFORMATICS\;OLYMPIAD} \]

第 $1$ 章绪论
第 $2$ 章 从无解出发
第 $3$ 章 “艰苦朴素永不忘”
- $3.1$ 模拟
- $3.2$ 万能钥匙——DFS
第 $4$ 章 骗分的关键——猜想
- $4.1$ “听天由命”
- $4.2$ 猜测答案
- $4.3$ 寻找规律
- $4.4$ 小数据杀手——打表
第 $5$ 章 做贪心的人
- $5.1$ 贪心的算法
- $5.2$ 贪心地得分
第 $6$ 章 Cpp 的福利
- $6.1$ 算法库（函数）
- $6.2$ STL
  - $6.2.1$ std::vector
  - $6.2.2$ ``
第 $7$ 章 “宁为玉碎，不为瓦全”
第 $8$ 章 实战演练（例子）
- $8.1$ CSP-J 2021
- $8.2$ CSP-S 2024
第 $9$ 章结语

\[\LARGE \text{第}\,1\,\text{章}\quad\text{绪论} \]

在 OIer 中，有两个定理广为流传：

著名的 lzn 定理：任何蒟蒻必须经过大量的刷题练习才能成为大牛乃至于大犇；
单调队列定理：OI 圈若是单调队列，那么即使有比你小，或比你强的，你都能被接受；但是，绝不能有比你小也比你强的。

然而，我们这些蒟蒻们，没有经过那么多历练，却要和大犇、和比你小的天才们同场竞技，我们该怎么以弱胜强呢？答案就是：骗分！

那么，骗分是什么呢？就是用简单的程序（比标算简单很多，保证~~大多数~~人能轻松搞定的程序），尽可能多得拿（pian）到部分分，甚至发现题目解法。

让我们走进《骗分新论 》，来学习骗分的技巧，来挑战大奖吧！

\[\Large \text{第}\,2\,\text{章}\quad\text{从无解出发} \]

在很多题目中都有类似于这样的话：

若无解，请输出 -1。

看到这句话时，骗分的蒟蒻们就欣喜若狂，因为——数据中很可能会有无解的情况！~~But，有很多题为了防骗分没有无解数据或是多测（~~

那么，只要在程序里打出下面这一行代码：

cout << -1;

就能得到最少一个测试点的分，甚至更多！

如：

[NOIP2012 普及组] 文化之旅

题目描述

有一位使者要游历各国，他每到一个国家，都能学到一种文化，但他不愿意学习任何一种文化超过一次（即如果他学习了某种文化，则他就不能到达其他有这种文化的国家）。不同的国家可能有相同的文化。不同文化的国家对其他文化的看法不同，有些文化会排斥外来文化（即如果他学习了某种文化，则他不能到达排斥这种文化的其他国家）。

现给定各个国家间的地理关系，各个国家的文化，每种文化对其他文化的看法，以及这位使者游历的起点和终点（在起点和终点也会学习当地的文化），国家间的道路距离，试求从起点到终点最少需走多少路。

输入格式

第一行为五个整数 $N,K,M,S,T$，每两个整数之间用一个空格隔开，依次代表国家个数（国家编号为$1$ 到 $N$），文化种数（文化编号为 $1$ 到 $K$），道路的条数，以及起点和终点的编号（保证 $S$ 不等于 $T$）；

第二行为 $N$个整数，每两个整数之间用一个空格隔开，其中第 $i$个数 $C_i$，表示国家 $i$的文化为 $C_i$。

接下来的 $K $行，每行 $K$ 个整数，每两个整数之间用一个空格隔开，记第$ i$ 行的第 j 个数为 $a_{ij}$，$a_{ij}= 1$ 表示文化 $i$ 排斥外来文化$ j$（$i$ 等于 $j$ 时表示排斥相同文化的外来人），$a_{ij}= 0$ 表示不排斥（注意 $i$ 排斥 $j$ 并不保证 $j$ 一定也排斥 $i$）。

接下来的 $M$ 行，每行三个整数 $u,v,d$，每两个整数之间用一个空格隔开，表示国家 $u$与国家 $v $有一条距离为$ d $的可双向通行的道路（保证$ u $不等于 $v$，两个国家之间可能有多条道路）。

输出格式

一个整数，表示使者从起点国家到达终点国家最少需要走的距离数（如果无解则输出$-1$）。

样例 #1

样例输入 #1
2 2 1 1 2 
1 2 
0 1 
1 0 
1 2 10
样例输出 #1
-1
样例 #2

样例输入 #2
2 2 1 1 2 
1 2 
0 1 
0 0 
1 2 10
样例输出 #2
10
提示

输入输出样例说明$1$

由于到国家 $2$ 必须要经过国家 $1$，而国家 $2$ 的文明却排斥国家 $1$ 的文明，所以不可能到达国家 $2$。

输入输出样例说明$2$

路线为 $1 \rightsquigarrow 2$。

【数据范围】

对于 $100\%$ 的数据，有

$2≤N≤100$，

$1≤K≤100$，$1≤k_i≤K$，

$1≤M≤N^2$，

$1≤u, v≤N$，

$1≤d≤1000,S≠T,1≤S,T≤N$

对于此题，只输出 -1 可以得 $10$ 分。（

现在，你已经掌握了最基础的骗分技巧。只要你会基本的输入输出语句，你就能实现这些骗分方法。

如果你有一定的基础，请看下一章——我将教你怎样用简单方法骗取部分分数。

\[\LARGE \text{第}\,3\,\text{章}\quad\text{“艰苦朴素永不忘”} \]

本章的标题来源于《学习雷锋好榜样》的一句歌词，但我不是刻意教导你们学习雷锋精神，而是学习骗分！

看到 “朴素” 这两个字了吗？它们代表了一类算法，主要有模拟和 DFS。下面我就来介绍它们在骗分中的应用。

$3.1$ 模拟

所谓模拟，就是用计算机程序来模拟实际的事件。
例如 [NOIp 2017 提高组] 时间复杂度，题意简而言之就是写一个程序来模拟一个简化程序的运行。

较繁甚至毒瘤的模拟就不叫骗分了，这里也不再讨论这个问题。

模拟主要可以：

骗数据结构题上的分，例如线段树、树状数组等；
骗任何可以打出模拟代码的分（废话

下面举一个例子。

[USACO07JAN] Balanced Lineup G

题目描述

每天，Farmer John 的 $n\ (1\le n\le 5\times 10^4)$ 头牛总是按同一序列排队。

有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊，牛的身高不应该相差太大。John 准备了 $q(1\le q\le 1.8\times10^5)$ 个可能的牛的选择和所有牛的身高 $h_i(1\le h_i\le 10^6,1\le i\le n)$。他想知道每一组里面最高和最低的牛的身高差。

输入格式

第一行两个数 $n,q$。

接下来 $n$ 行，每行一个数 $h_i$。

再接下来 $q$ 行，每行两个整数 $a$ 和 $b$，表示询问第 $a$ 头牛到第 $b$ 头牛里的最高和最低的牛的身高差。

输出格式

输出共 $q$ 行，对于每一组询问，输出每一组中最高和最低的牛的身高差。

样例输入 #1
6 3
1
7
3
4
2
5
1 5
4 6
2 2
样例输出 #1
6
3
0

对于这个例子，可以写线段树，也可以写 ST。而我们这种蒟蒻，就模拟吧。

附部分模拟程序：

cin.tie(0) -> sync_with_stdio(0);
// 输入 h[i]
for(int i=1; i<=q; ++i){
    cin >> a >> b;
    int minn=INT_MAX, maxn=INT_MIN;
    for(int i=a; i<=b; ++i){
        if (h[i] < minn){
            minn = h[i];
        } else if (h[i] > maxn){
            maxn = h[i];
        }
    }
    cout << maxn-minn;
}

程序简洁明了，并且能高效骗分。本程序可得 $\bf50$ 分。

$3.2$ 万能钥匙——DFS

$\texttt{DFS}$ 是图论中的重要算法。DFS 序可以用来求 LCA，转化树上问题（树链剖分），难度跨度极大。

但在我们看来，关键就是如何骗分。

这对于你的骗分是至关重要的。比如说，一些 DP 题，可以 DFS；数学题，可以 DFS；图论的巧题，还能 DFS。
下面以一道极其简单的 DP 题为例，解释一下 DFS 骗分。

[NOIP2005 普及组] 采药

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 $2$ 个整数 $T$（$1 \le T \le 1000$）和 $M$（$1 \le M \le 100$），用一个空格隔开，$T$ 代表总共能够用来采药的时间，$M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间（包括 $1$ 和 $100$）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

样例输入 #1
70 3
71 100
69 1
1 2
样例输出 #1
3
提示

对于 $30\%$ 的数据，$M \le 10$；

对于全部的数据，$M \le 100$。

我们瞄准 $30\%$ 的数据来做，可以用 DFS 枚举方案，然后模拟计算出最优解。

附一个大致的代码：

void DFS(int d, int c){
    if(d == n) {
        ans = min(c, ans);
        return ;
    }
    DFS(d+1, c+w[i]);
    DFS(d+1, c);
}

虽然大佬们可以秒掉这题，但是我们（即使你成为了大佬）打暴力却很有必要，这有利于我们想到怎么优化。

例如类似于这题的动态规划题，利用空间换时间的思想，将上面的没有回溯（即无后效性）的暴搜记忆化，得分会大大提高（不需要太成熟的思路，但常数略大），甚至得到满分。

\[\LARGE\text{第}\,4\,\text{章}\quad\text{骗分的关键——猜想} \]

$4.1$ 听天由命

如果你觉得你 RP 很好，可以试试这一招—— 输出随机数。

先看一下代码：

#include <bits/extc++.h>
using namespace std;

int main() {
    mt19937 rnd(time(nullptr));
    cout << rnd();
    return 0;
}

这种方法适用于输出一个整数（或判断是否）的题目中，答案的范围越小越好。
让老天决定你的得分吧。(

$4.2$ 猜测答案

有些时候，问题的答案可能很有特点：对于大多数情况，答案是一样的。这时，骗分就该出手了。你需要做的，就是发掘出这个答案，然后直接输出。

例如，2022 年，吃薯片杠哀思中有一道题：

[CSP-S 2022] 星战

题目描述

在这一轮的星际战争中，我方在宇宙中建立了 $n$ 个据点，以 $m$ 个单向虫洞连接。我们把终点为据点 $u$ 的所有虫洞归为据点 $u$ 的虫洞。

战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：

敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。

敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。

注意：摧毁只会导致虫洞不可用，而不会消除它的存在。

为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：

A 型特种部队则可以将某个特定的虫洞修复。

B 型特种部队可以将某据点的所有损坏的虫洞修复。

考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。

我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。

为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：

如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以实现反击。

为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当只有一个从该据点出发的虫洞可用时，这个据点可以实现连续穿梭。

如果我方所有据点都可以实现反击，也都可以实现连续穿梭，那么这个时刻就是一个绝佳的反攻时刻。

总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次反攻。

输入格式

输入的第一行包含两个正整数 $n,m$。

接下来 $m$ 行每行两个数 $u,v$，表示一个从据点 $u$ 出发到据点 $v$ 的虫洞。保证 $u \ne v$，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。

接下来一行一个正整数 $q$ 表示询问个数。

接下来 $q$ 行每行表示一次询问或操作。首先读入一个正整数 $t$ 表示指令类型：

若 $t = 1$，接下来两个整数 $u, v$ 表示敌人摧毁了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且未被摧毁。

若 $t = 2$，接下来一个整数 $u$ 表示敌人摧毁了据点 $u$。如果该据点的虫洞已全部被摧毁，那么这次袭击不会有任何效果。

若 $t = 3$，接下来两个整数 $u, v$ 表示我方修复了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且被摧毁。

若 $t = 4$，接下来一个整数 $u$ 表示我方修复了据点 $u$。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。

在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。

输出格式

输出一共 $q$ 行。对于每个指令，输出这个指令执行后能否进行反攻。

样例输入 #1
3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2
样例输出 #1
NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO
提示

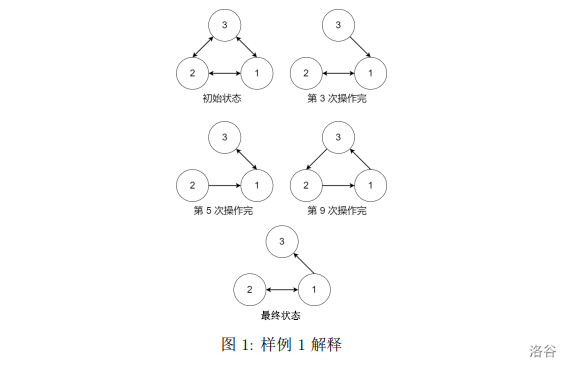
样例解释

虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：

数据范围

对于所有数据保证：$1 \le n \le 5 \times {10}^5$，$1 \le m \le 5 \times {10}^5$，$1 \le q \le 5 \times {10}^5$。

根据思考，我们发现，可以反攻的条件较为苛刻，所以我们可以直接想到：对于每一次询问，输出 NO。

这样写法，在官方数据下，可得 $\bf{45}$ 分。这样高的得分，甚至塑造了一个名梗。

现在知道猜测答案的厉害了吧？

不过有时，你需要运用第 $3$ 章中学到的知识，先写出朴素算法，然后造一些数据，可能就会发现规律，甚至是满分解法！（如下文 4.4

$4.3$ 寻找规律

宇宙安全声明：本节讲的规律不是正当的算法规律，而是数据的特点。

某些题目会给你很多样例，你就可以观察他们的特点了。有时，数据中的某一个（或几个）数，能通过简单的关系直接算出答案。

只要你找到了规律，在很多情况下你都能得到可观的分数。

这样的题目大多出现在较高等级的比赛中，本人蒟蒻一个，就不举例了。

4.4 小数据杀手——打表

打表，一门门道很深的骗分道路。以最基础的情况为例，它适用于数据小，答案可能性少的时候；但需要一定的码力。

表虽然不能乱打，但还是很有用的。

普通打表：$O(1)$ 复杂度

先看一个例子：

[NOIP2003 普及组] 栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

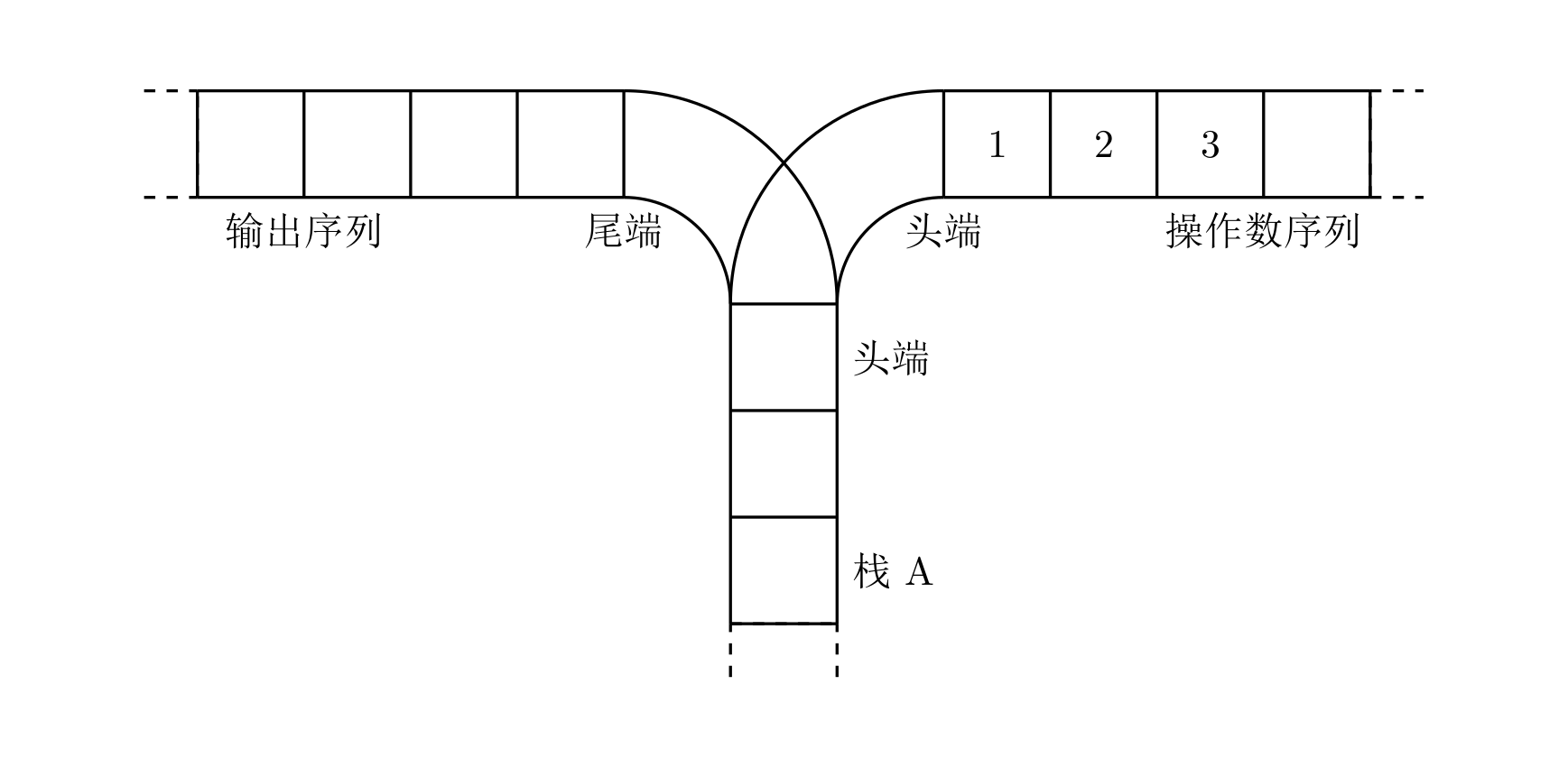
宁宁考虑的是这样一个问题：一个操作数序列，$1,2,\ldots ,n$（图示为 1 到 3 的情况），栈 A 的深度大于 $n$。

现在可以进行两种操作，

将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）

将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

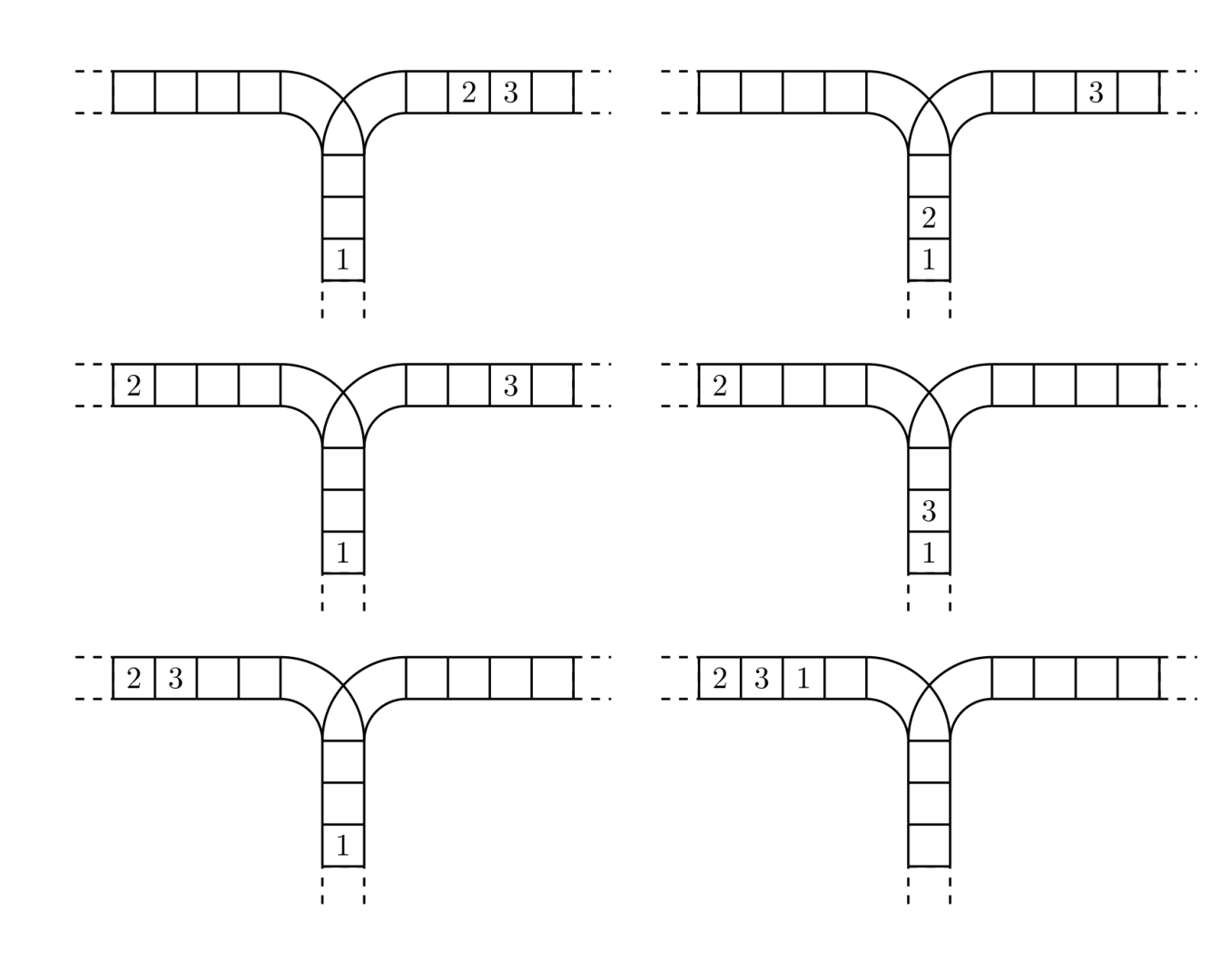
使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

（原始状态如上图所示）

你的程序将对给定的 $n$，计算并输出由操作数序列 $1,2,\dots,n$ 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 $n$（$1 \le n \le 18$）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例输入 #1
3
样例输出 #1
5

这题看似复杂，但数据范围太小。我们可以将暴力搜索的代码改成表程，程序就好写了：

#include <bits/stdc++.h>
int a[18]={1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790,477638700}, n;
int main(){
    std::cin >> n;
    std::cout << ans[n-1];
}

测试结果不言而喻，AC 了。

高级打表：辅助思考

upd：手滑打错周期了，痛失 $80$ 分，1= 废了！
upd2：文件名打错了，痛失 $100$ 分，4 了！/dk

来看看我考 CSP-J 的那一年的 T3——小木棍：

题目描述

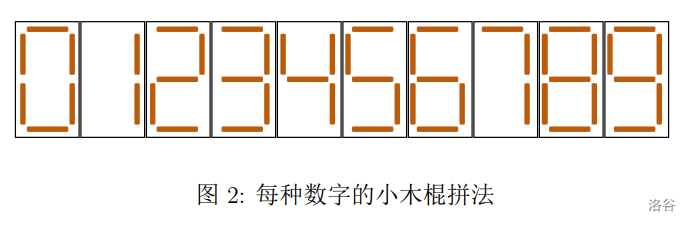
小 S 喜欢收集小木棍。在收集了 $n$ 根长度相等的小木棍之后，他闲来无事，便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。

现在小 S 希望拼出一个正整数，满足如下条件：

拼出这个数恰好使用 $n$ 根小木棍；

拼出的数没有前导 $0$；

在满足以上两个条件的前提下，这个数尽可能小。

小 S 想知道这个数是多少，可 $n$ 很大，把木棍整理清楚就把小 S 折腾坏了，所以你需要帮他解决这个问题。
如果不存在正整数满足以上条件，你需要输出 $-1$ 进行报告。

输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 $T$，表示数据组数。

接下来包含 $T$ 组数据，每组数据的格式为：一行一个整数 $n$，表示木棍数。

输出格式

对于每组数据：输出一行，如果存在满足题意的正整数，输出这个数；否则，输出 $-1$。

样例输入 #1
5
1
2
3
6
18
样例输出 #1
-1
1
7
6
208
提示

【样例 1 解释】

对于第一组测试数据，不存在任何一个正整数可以使用恰好一根小木棍摆出，故输出 $-1$。

对于第四组测试数据，注意 $0$ 并不是一个满足要求的方案。摆出 $9$、$41$ 以及 $111$ 都恰好需要 $6$ 根小木棍，但它们不是摆出的数最小的方案。

对于第五组测试数据，摆出 $208$ 需要 $5 + 6 + 7 = 18$ 根小木棍。可以证明摆出任何一个小于 $208$ 的正整数需要的小木棍数都不是 $18$。注意尽管拼出 $006$ 也需要 $18$ 根小木棍，但因为这个数有前导零，因此并不是一个满足要求的方案。

【数据范围】

对于所有测试数据，保证：$1 \leq T \leq 50$，$1 \leq n \leq \color{red}{10^5}$。

测试点编号 $n\leq$ 性质

$1$ $20$ 无

$2$ $50$ 无

$3$ $10^3$ A

$4,5$ $10^5$ A

$6$ $10^3$ B

$7,8$ $10^5$ B

$9$ $10^3$ 无

$10$ $10^5$ 无

性质 A：保证 $n$ 是 $7$ 的倍数且 $n \geq 100$。

性质 B：保证存在整数 $k$ 使得 $n = 7k + 1$，且 $n \geq 100$。

测试点编号	\(n\leq\)	性质
\(1\)	\(20\)	无
\(2\)	\(50\)	无
\(3\)	\(10^3\)	A
\(4,5\)	\(10^5\)	A
\(6\)	\(10^3\)	B
\(7,8\)	\(10^5\)	B
\(9\)	\(10^3\)	无
\(10\)	\(10^5\)	无

这是一道解法较多的题。DP，贪心，等等都能解。

考虑枚举所有数字（0 到 9）的个数，预处理所有答案。显然会超时。

不过，我们可以打表...... 等等，$10^5$ 的数据，如何打表？暴力在考场上可能都跑不完，还要写高精度，表长还可能到 100 K。

这时候，大多数人当然可以打 $n \le 20$ 的表，艹个 $10$ 分，争 T4 暴搜抢 1=。

但是由于 T4 的毒瘤，加上我在 GD，想 1=，T3 只有 $10 \text{ pts}$ 是远远不够的。
~~然后我就大挂分，无缘 1=。控诉 CCF 不给 T3 大样例！但，也许我不配。~~

我是以下面的方式做出此题的。

不过，我们可以把表打稍大一点，到 $n\le50$。（懒得再打一遍，这里借用了题解区中的一张图片的部分）

这时你可以发现一个惊人的规律（甚至不用打完就可以发现）：

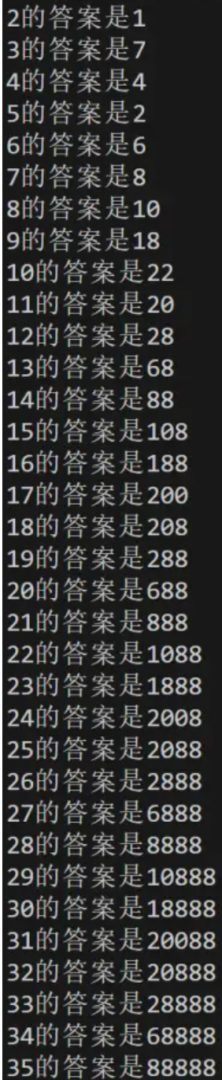
从 $22$ 开始，末尾的 $8$ 逐渐有规律的变多。

又发现，周期为 $\bf7$，在 $n\ge20$ 时，可以通过在 $n\in[8,14]$ 的结果的数后添 $8$ 得到。（要看好间隔！5555）

所以，我们可以直接打出 $n\le 21$ 的表 $a$，再根据 $a_{n \bmod 7 + 8}$ 的值，不断在其末尾添 $8$，直到不能再添为止。

这也就是后文所说的贪心思想。突然正解化了属于是。

最后，这里 要用 string 存数字，否则会爆炸。期望得分 $\bf 100\textbf{ pts}$。

总之，打表是很有用的。

学完这一章，你已掌握了一些有用的骗分技巧。如果你在有一定的算法基础，最起码可以在 CSP-J 艹到 220 分以上了。

下面的内容涉及一点算法知识，难度有所增加。几乎只能做大水题的~~和只会 ctj 的~~可以止步于此了。

\[\LARGE \text{第}\ 5\ \text{章}\quad\text{做贪心的人} \]

5.1 贪心的思想

给你一堆奖，让你挑一个，相信你一定会挑自己认为最好的。其实，这就是贪心思想。

贪心是个简单而又极复杂的思想，但你现在先不用管那么多。我们只关心骗分。

这种方法在在 DP 题中骗分时，较为有用。如 3.2 中的例子，使用贪心也可以骗去一定的分。

不过，这种假算的得分与数据强度有很大联系，请在大赛中谨慎使用。

$5.2$ 贪心地得分

我们已经学了很多骗分方法，但他们中的大多效率并不高，一般能骗 $10\sim 20$ 分。这不能满足我们的贪心。

我们可以组合骗分的程序。这样也许能拿到多一点的分。当然，合并骗分方法时要注意，不要重复骗同一种情况，或漏考虑一些情况。也要注意细节，不要“一着不慎，满盘皆输”。

骗分集大成者——“面向数据范围” 的编程，在数据点分段明显时，极其有用。

这不仅可以防止正解或高分解挂分影响得小数据的分，还能让自己的代码有条理，便于理清思路。大佬应该也爱这么写吧（不是

大量能骗分的问题都能用上述方法。大家可以试试用新方法骗 $2.1$ 中的例子，NOIP 2012 PJ 组 T3——文化之旅。

下文将讲述一些（C++14 及其之前的）小技巧，可以帮助你节省码量。

\[\LARGE \text{第}\,6\,\text{章}\quad\texttt{C++}\,\text{的福利} \]

在 C++ 中，有两个好东西。

其一，名唤 STL（Standard Template Library，标准模板库）；
其二，名唤算法库，主要包含 <numeric> 和 <algorithm> 等头文件。

这些东西受 OIer 们喜爱，推崇。

（注意：这里与主题相关度较低，之后可能会拆分）

6.1 算法库中的函数

太简单的，人尽皆知的，将不再次提及。

施工 ing。

6.2 STL

注意：STL 人傻常数大，在时间效率吃紧的情况下（尤其是没有 -O2 时）请少用（或卡常）。数据量大时，一个快读/输可能就可以加快 50+ ms！

6.2.1 `std::vector`

C++ 里有一种东西，叫 vector 容器。它好比如意金箍棒，可以随着元素的数量而改变大小。

它其实就类似于数组，却比数组强得多，但常数较大。

下面看看它的几种操作：

vector<int> V(n, 0);//定义，后面括号可以不写。第一个参数表示大小，第二个为初始值。
V.push_back(x);//末尾增加一个元素x
V.pop_back();//末尾删除一个元素
V.size();//返回容器中的元素个数

它同样可以使用下标访问。（从 $0$ 开始）

6.2.2

施工ing。

\[\Large \text{第}\,7\,\text{章}\quad\text{“宁为玉碎，不为瓦全”} \]

至此，我已介绍完了我所知的骗分方法和小技巧。如果上面的方法都不奏效，我也无能为力。

\[\LARGE \text{第}\,8\,\text{章}\quad\text{实战演练} \]

下面我们来做一些习题，练习我们学过的骗分技巧。

来一起分析一下 CCF CSP-J/S 的历年真题吧。

8.1 CSP-J 2021

（题目详情略）

第 $1$ 题，枚举可能拿到的糖果数。期望得 $70$ 分。实际上，这道题很简单，轻松 $100$ 分。
第 $2$ 题，暴力完成每一个操作，得 $36$ 分。~~优化一下好像可以拿 76 分。~~
第 $3$ 题，是一道磨你题，得分得看自己的修行了。（
第 $4$ 题，可以暴力模拟取水果的操作，得 $[10,70]$ 分。（这题的做法非常多，各种数据结构维护好像都可以）

这样下来，一共得 $[116,216] + x$ 分，最低的分数已经比部分省的 2= 要高了！(

甚至往上一点就是大部分省的 1= 的分数线！

8.2 CSP-S 2024

（题目详情略）

第一题，简单。手玩样例，写暴力模拟，再自己造数据，可发现答案即为战斗力的众数的出现次数。（其实是正确解法！可证明）可得 $\bf100$ 分；（可我赛时没拿到 /ll
第二题，特殊性质 A 贪心问题 + 前两个测试点枚举，得 $\bf40$ 分；（这题也是 PJ 题，可我没调配好二分，Joker
第三题，看到动态规划，先暴力 DFS，可得 $\bf20$ 分。也可想到朴素二维 dp，可得 $50$ 分，优化空间后可得 $65$ 分；
第四题，太难。个人觉得，除随机数和找规律外，无法通过较简单手段（PJ 组水平算法）骗分。

总分 $[160,205]$ 分。这很接近甚至超过 6 级勾的一个水平了（差一点，还是要学的），在大部分省里，你已经可以拿 1=，领先许多人~~包括我这个畜二生~~了！你的信心一定会得到鼓舞的。

这就是骗分的神奇之处。

\[\LARGE \text{第}\ 9\ \text{章}\quad\text{结语} \]

骗分是蒟蒻的有力武器，~~可以在比赛中骗得大量分数~~。相信大家在这篇文章中收获了很多，希望本文能帮助你在考试时多得一些分，助力你完成竞赛入门。

但是，最后还是要说一句：

\[\Large \color{3498db}\text{不骗分，是骗分的最高境界。} \]

posted @ 2025-07-25 03:21 RedAccepted 阅读(30) 评论(0) 收藏举报

刷新页面返回顶部

NewbieZZZ

骗分论 2

目录

[NOIP2012 普及组] 文化之旅

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

输入输出样例说明\(1\)

输入输出样例说明\(2\)

\(3.1\) 模拟

[USACO07JAN] Balanced Lineup G

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

\(3.2\) 万能钥匙——DFS

[NOIP2005 普及组] 采药

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

提示

\(4.1\) 听天由命

\(4.2\) 猜测答案

[CSP-S 2022] 星战

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

提示

样例解释

数据范围

\(4.3\) 寻找规律

4.4 小数据杀手——打表

普通打表：\(O(1)\) 复杂度

[NOIP2003 普及组] 栈

题目背景

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

高级打表：辅助思考

题目描述

输入格式

输出格式

样例输入 #1

样例输出 #1

提示

5.1 贪心的思想

\(5.2\) 贪心地得分

6.1 算法库中的函数

6.2 STL

6.2.1 std::vector

6.2.2

8.1 CSP-J 2021

8.2 CSP-S 2024

公告

6.2.1 `std::vector`