各种建图优化

\(n\) 个点的有向图，\(m\) 次加边操作。
每次可以由 \([l,r]\) 内的所有点向 \(u\) 点连一条权为 \(w\) 的边，或者由 \(u\) 向 \([l,r]\) 内所有点连一条权为 \(w\) 的边。

求出所有操作之后以给定一点开始的最短路。

线段树优化建图

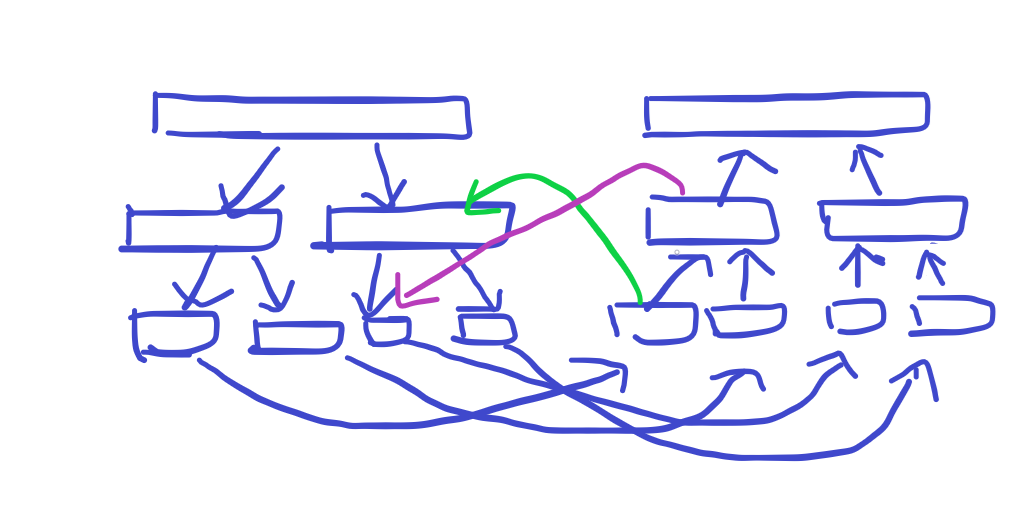
两棵树，边的方向相反。蓝边权值为 \(0\)，红绿边权值为 \(w\)。

时间复杂度单次操作 \(\mathcal{O}(\log n)\)。

如果是区间向区间连边，复杂度应该是 \(\mathcal{O}(\log^2n)\)，暂时我还想不到进一步的优化方法。

---

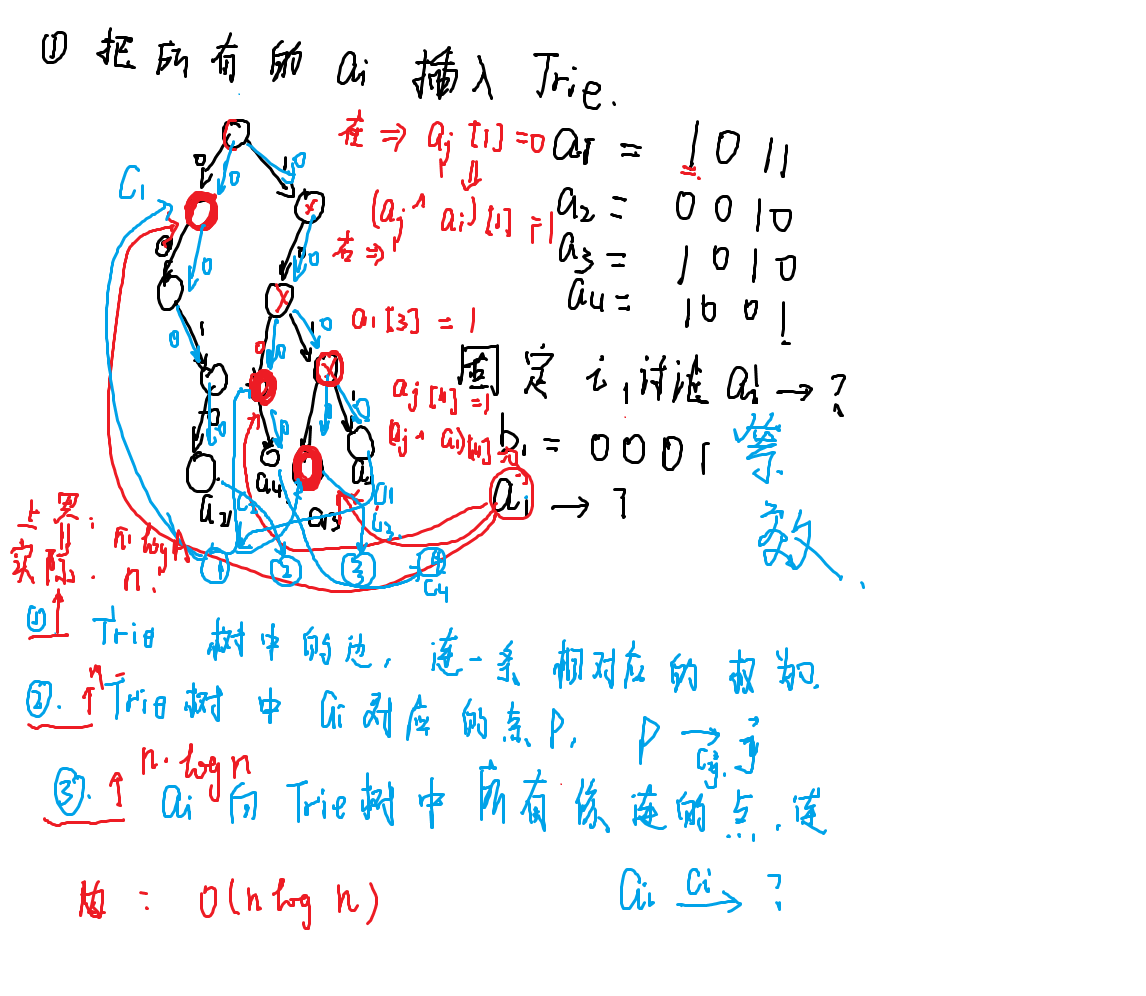
\(n\) 个点的有向图，每个点都有点权 \(a_u\)，\(m\) 次加边操作。

每次可以由 \(u\) 向所有 \(a_v\ \text{xor}\ a_u\ge c\) 的 \(v\) 连一条权为 \(w\) 边。

求出所有操作之后以给定一点开始的最短路。

Trie 树优化建图