「题解」小胡的硬币

描述

小胡站在原点，手里拿着两枚硬币。抛第一枚硬币正面向上的概率为 \(p\)，第二枚正面向上的概率为 \(q\)。

小胡开始抛第一枚硬币，每次抛到反面小胡就向 \(x\) 轴正方向走一步，直到抛到正面。

接下来小胡继续抛第一枚硬币，每次抛到反面小胡就向 \(y\) 轴正方向走一步，直到抛到正面。

现在小胡想回来了，于是他开始抛第二枚硬币，如果小胡抛到正面小胡就向 \(x\) 轴的负方向走一步，否则小胡就向 \(y\) 轴的负方向走一步。

现在小胡想知道他在往回走的时候经过原点的概率是多少呢？

思路

小胡从原点走到 \(x\) 坐标为 \(x\) 的点的概率为 \((1-p)^x\cdot p\)；

假设小胡现在的 \(x\) 坐标为 \(x\)，小胡走到 \(y\) 坐标为 \(y\) 的点的概率为 \((1-p)^y\cdot p\)；

假设小胡现在位于 \((x,y)\)，小胡走回原点的概率为 \(q^x\cdot (1-q)^y\cdot\binom{x+y}{x}\)。

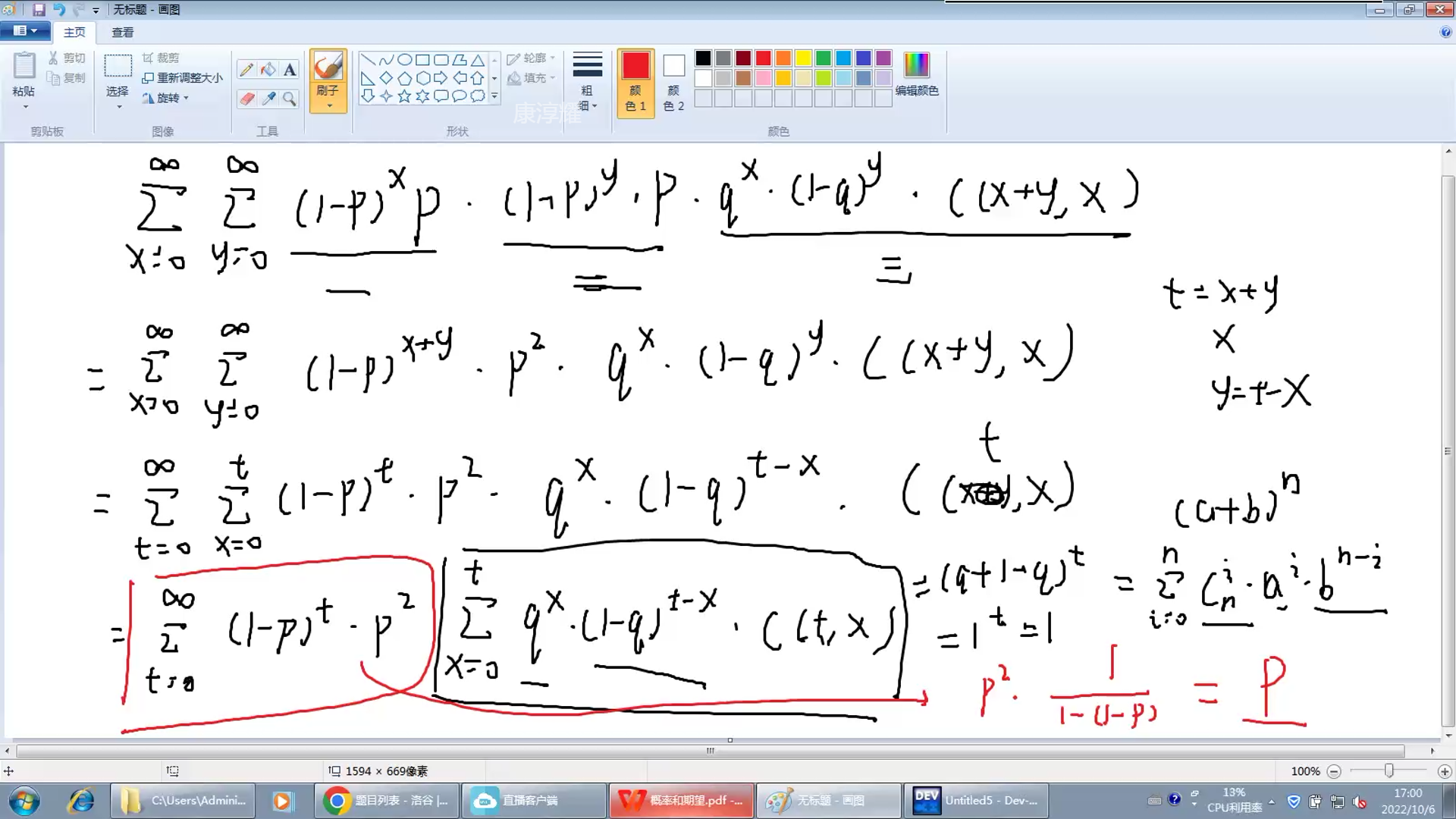
所以，小胡走到任意点又走回原点的概率为：

\[P=\sum_{x=0}^{\infty}\sum_{y=0}^{\infty}(1-p)^x\cdot p\cdot (1-p)^y\cdot p\cdot q^x\cdot (1-q)^y\cdot\binom{x+y}{x} \]

令 \(t=x+y\)，得：

\[P=\sum_{t=0}^{\infty}\sum_{x=0}^{t}(1-p)^t\cdot p^2\cdot q^x\cdot (1-q)^{t-x}\cdot\binom{t}{x} \]

整理，得：

\[P=\sum_{t=0}^{\infty}(1-p)^t\cdot p^2\cdot\sum_{x=0}^{t} q^x\cdot (1-q)^{t-x}\cdot\binom{t}{x} \]

根据二项式定理化简，得：

\[P=\sum_{t=0}^{\infty}(1-p)^t\cdot p^2 \]

根据等比数列求和公式化简，得：

\[P=p \]