PTA大作业四和期中考试总结
面对对象程序设计————PTA前三次作业总结
期中考试——题目集1
整体总结:
题目集01-03考察的是继承与多肽,以及抽象类函数的使用,并且考察了对类图的理解。
题目集1 7-1 点与线(类设计)
整体思路分析 :
1.本题逻辑十分清晰,无十分严重的踩坑;
2.本题主要要求实现对类Point,类Line的创建;
3.对于私有数据的使用,要注意其使用范围只能在类中使用;
核心代码分析:
1.类Point
class Point { private double x=0; private double y=0; Point(double x,double y) { if(x>0&&x<=200&&y>0&&y<=200)//判断数据是否符合要求 { this.x=x; this.y=y; } } public double getX()//获取私有数据y { return x; } public void setX(double x0)//修改私有数据y { x=x0; } public double getY()//获取私有数据y { return y; } public void setY(double y0)//修改私有数据y { y=y0; } public void display()//展示x,y { System.out.printf("%.2f %.2f", x,y); } }
2.类Line
class Line { private Point point1; private Point point2; private String color; Line(Point p1,Point p2,String color)//构造函数 { point1=p1; point2=p2; this.color=color; } public Point getPoint1()//获取私有数据 { return point1; } public void setPoint1(Point p)//修改私有数据 { point1=p; } public Point getPoint2()//获取私有数据 { return point2; } public void setPoint2(Point p)//修改私有数据 { point2=p; } public String getColor()//获取私有数据 { return color; } public void setColor(String p)//修改私有数据 { color=p; } public double getDistance()//返还距离 { return Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getY()-point2.getY(),2)); } public void display()//展示 { if(point1.getX()!=0&&point1.getY()!=0&&point2.getX()!=0&&point2.getY()!=0) { System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); System.out.println("("+String.format("%.2f", point1.getX())+","+String.format("%.2f", point1.getY())+")"); System.out.println("The line's end point's Coordinate is:"); System.out.println("("+String.format("%.2f", point2.getX())+","+String.format("%.2f", point2.getY())+")"); System.out.print("The line's length is:"); System.out.printf("%.2f", Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getY()-point2.getY(),2))); } else System.out.print("Wrong Format"); } }
缺陷:
1.在进行展示的时候没有理清Point中display的作用,把要求的展示全部集中于Line中了;
改进建议:
1.类中获取私有数据的方法重复度高,需要采取方法降低其复杂度。
题目集1 7-2 点线面问题重构(继承与多态)
整体思路分析:
1.本题主要要求实现对类Point,类Line,类Plane,以及抽象类Element的创建;
2.主要需要注意抽象类方法的使用;
度量分析
圈复杂度分析使用 SourceMonitor 软件
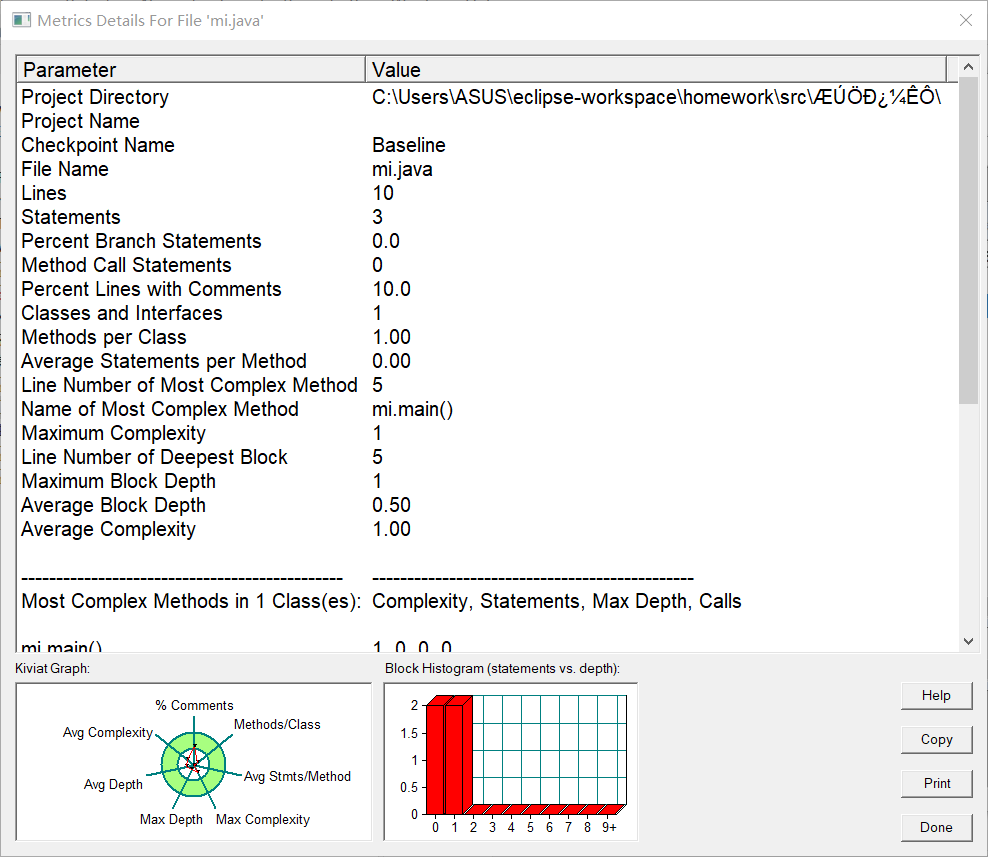
核心代码分析
1.抽象类Element的建立
abstract class Element { public abstract void display();//抽象方法的建立 }
2.类Plane的建立
class Plane extends Element//继承抽象类 { private String color; Plane(String color)//构造函数 { this.color=color; } public String getcolor()//获取私有数据 { return color; } public void setcolor(String c)//改变私有数据 { color=c; } public void display()//展示 { System.out.println("The Plane's color is:"+color); } }
类Point,以及类Line与7-1中基本一样,不作分析
踩坑点:
1.抽象类的使用不熟练,需要翻书才能确定其使用的正确方式。
改进建议:
多尝试一些复杂的抽象类题目,增强自己对其了解程度。
题目集1 7-3 点线面问题再重构(容器类)
整体思路分析:
1.本题主要要求实现对类Point,类Line,类Plane,以及抽象类Element的创建,与7-2一致,但多了一个容器类GeometryObject的创建和使用
2.主要需要注意抽象类方法的使用;
3.本题考察了对ArrayList类方法的使用;
度量分析
圈复杂度分析使用 SourceMonitor 软件
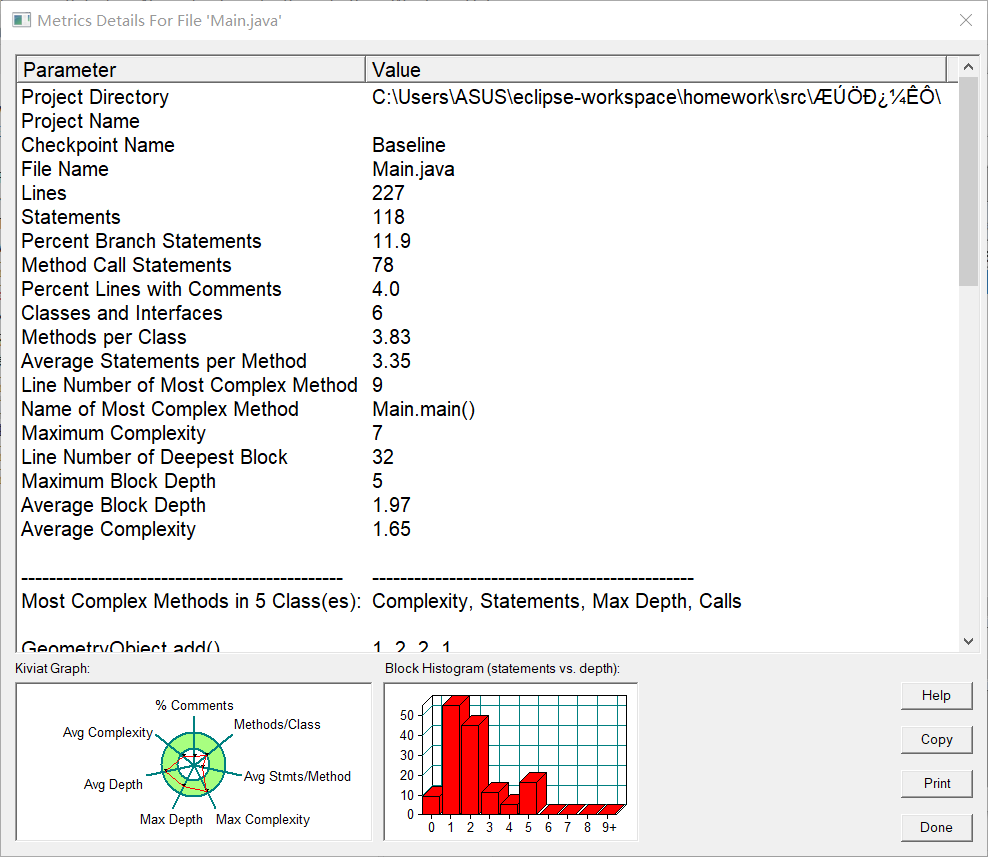
核心代码分析
1.Main函数
public static void main(String[] args) { Scanner in=new Scanner(System.in); GeometryObject t=new GeometryObject(); Point p1=new Point(in.nextDouble(),in.nextDouble()); t.add(p1); Point p2=new Point(in.nextDouble(),in.nextDouble()); t.add(p2); Point m1=new Point(in.nextDouble(),in.nextDouble()); t.add(m1); Point m2=new Point(in.nextDouble(),in.nextDouble()); t.add(m2); String color=in.next(); Line line=new Line(p1,p2,color); t.add(line); Plane plane=new Plane(color); t.add(plane); int choice = in.nextInt(); while(choice != 0) { switch(choice) { case 1: Point p3=new Point(in.nextDouble(),in.nextDouble()); t.add(p3); break; case 2: Point p4=new Point(in.nextDouble(),in.nextDouble()); Point p5=new Point(in.nextDouble(),in.nextDouble()); String color0=in.next(); Line line1=new Line(p4,p5,color0); t.add(line1); break; case 3: String color1=in.next(); Plane plane1=new Plane(color1); t.add(plane1); break; case 4: int index = in.nextInt(); t.remove(index); } choice = in.nextInt(); } t.list(); }
2.类GeometryObject的建立
class GeometryObject { private ArrayList<Element> list=new ArrayList<Element>() ;//建立列表 int dex=0; public void add(Element ele)//添加新对象 { list.add(ele); dex++; } public void remove(int dex)//删除对象 { list.remove(dex-1); } public void list()展示列表对象 { for( Element element : list) { element.display(); } } }
类abstract,类Point,类Plane以及类Line与7-2中基本一样,不作分析
踩坑点:
1.抽象类的使用不熟练,需要翻书才能确定其使用的正确方式。
2.忘记了将选择前确立的点,线,面数据加入列表中,而导致没有拿到全分
改进建议:
1.多尝试一些复杂的抽象类题目,增强自己对其了解程度。
2.写代码时遇到问题要冷静分析,不能因为时间而慌了手脚。
PTA大作业四——题目集2
整体总结:
此题目集难度陡然上升,每个题难度都很大,测试样例少并且测试点达到50之多,许多测试点都不能根据题目退出,得自己寻找边界数据测试然后进行修改,耗时很长。
题目集2 7-1 sdut-String-2 识蛟龙号载人深潜,立科技报国志
整体分析:
1.这一题的内容较简单,测试样例较少,仅需要简单的截取每排的数据进行相加在展示即可;
度量分析
圈复杂度分析使用 SourceMonitor
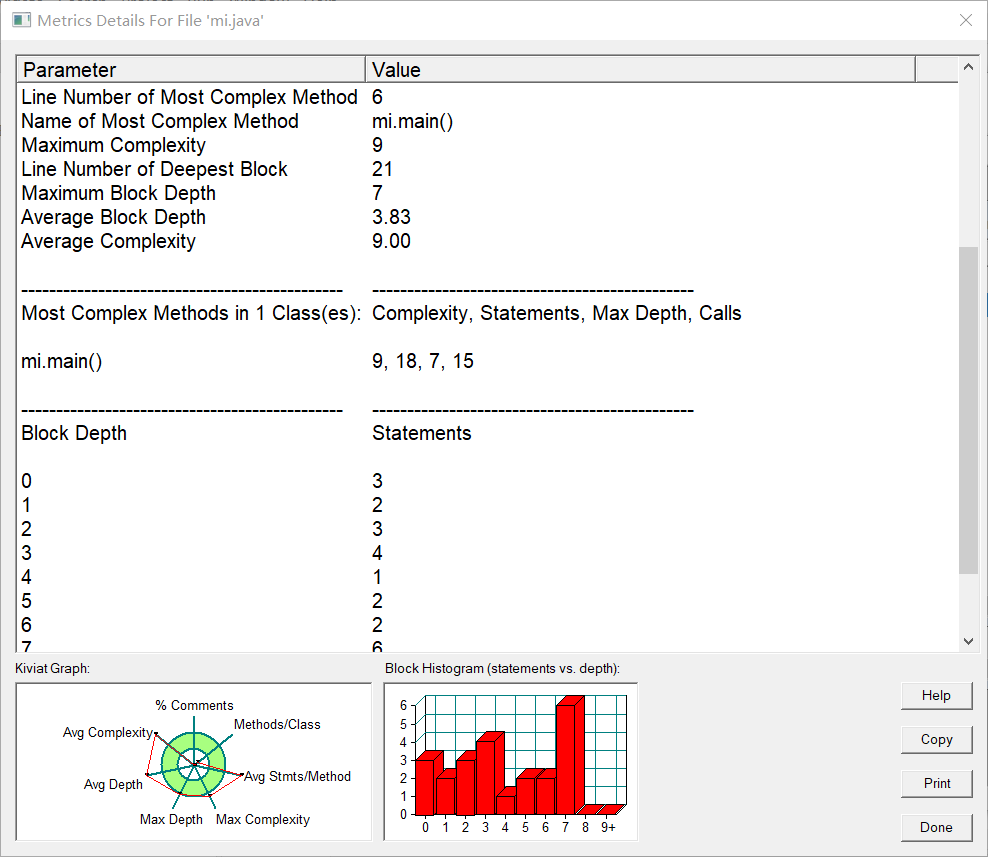
核心代码分析
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); String s =in.nextLine(); while(s!="end") { int sum=0; for (int i=0;i<s.length();i++) { if(s.charAt(i)>='0'&&s.charAt(i)<='9') { int j=i,k; for (k=j;k<s.length();k++) { if(s.charAt(k)<'0'||s.charAt(k)>'9') { i=k; String m =s.substring(j, k); sum=sum+Integer.parseInt(m); break; } else if(k==s.length()-1) { i=k; String m =s.substring(j, k+1); sum=sum+Integer.parseInt(m); break; } } } } s=in.nextLine(); System.out.println(sum); } } }
踩坑心得:
1.由于通过一个非0-9来判断截取数据的起点,另一个非0-9来判断结束的原因,导致一排最后的数据无法截取(最后没有字了);
改进建议:
1.无
题目集 7-2 点线形系列4-凸四边形的计算
整体分析
1.本题考察判断输入数据是否合法,以及判断是否是四边形、平行四边形,判断是否是菱形、矩形、正方形,判断是凹四边形(false)还是凸四边形(true),以及交点相关问题等平面问题;
2.此题涉及内容较多,且很多地方用到重复判断,所以采用建立各种方法进行判断, K(计算斜率),coinside(判断点重叠),Correct(判断是否合法输入)
3.判断输入数据是否合法:
题目明面上给的要求非常简单,但由于关于是否合法的要求没有完全给出,导致许多测试点都过不去。经过多次尝试,得出一下输入格式:
合法输入:(1)1,1 1,2 (2)+1,1 1,2 (3)1,1 1.0 1
非法输入:(1)++1,1 1,2 (2)+1+,1 1,2 (3)+01,1 1,2 (4).1,1 1,2 (5)1.,1 1,2 (6).,1 1,2 (7)+++,1 1,2 (8)000,1 1,1
点的数量坐标过多:(1)1,1 1,2 1,3
4.计算斜率:直接计算两直线斜率。斜率相同,返还0,斜率不同,返还1;
5.通过线段斜率以及线段长度来判断各种形状的判断;
6.coinside:通过Double.parseDouble(a[i])方法将传入的字符串转换为整数型,便于判断是否为同一点。
度量分析
6.选项1-4的主函数部分较简略,且无踩坑点,5的逻辑判断较为复杂;
圈复杂度分析使用 SourceMonitor
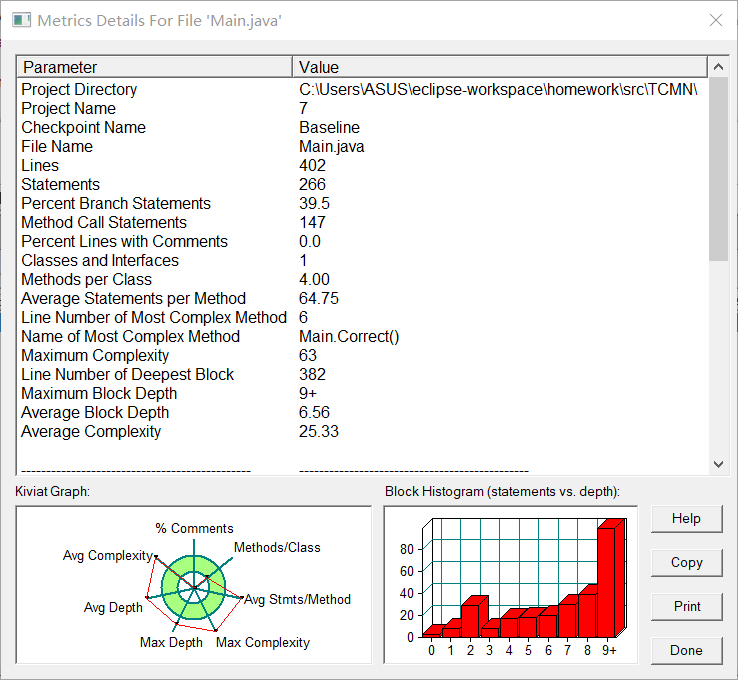
核心代码分析
斜率计算:
重合点判断:
public static int coinside(int x,String s)
{
int flag=1,i=0,j=0;
String[] a=s.split(" |,");
for(i=0;i<2*(x-1);i+=2)
{
double m1=Double.parseDouble(a[i]);
double n1=Double.parseDouble(a[i+1]);
for (j=i+2;j<2*x-1;j+=2)
{
double m2=Double.parseDouble(a[j]);
double n2=Double.parseDouble(a[j+1]);
if(m1==m2&&n1==n2)
flag=0;
}
}
return flag;
}
选项1:判断是否是四边形、平行四边形
if(flag2==0)
System.out.println("points coincide");//判断点重合
else
{
if(K(x1,y1,x2,y2,x2,y2,x3,y3)==1&&K(x2,y2,x3,y3,x3,y3,x4,y4)==1&&K(x3,y3,x4,y4,x1,y1,x4,y4)==1&&flag3==1)//判断相邻边斜率是否一致
{
System.out.print(true+" ");
if(K(x1,y1,x2,y2,x3,y3,x4,y4)==0&&K(x1,y1,x4,y4,x2,y2,x3,y3)==0)
System.out.print(true);
else
System.out.print(false);
}
else
System.out.print(false+" "+false);
}
选项2:判断是否是菱形、矩形、正方形
if(K(x1,y1,x2,y2,x2,y2,x3,y3)==1&&K(x2,y2,x3,y3,x3,y3,x4,y4)==1&&K(x3,y3,x4,y4,x1,y1,x4,y4)==1&&flag2==1&&flag3==1) { double c1=Math.pow(y2-y1, 2)+Math.pow(x2-x1, 2); double c2=Math.pow(y3-y2, 2)+Math.pow(x3-x2, 2); double c3=Math.pow(y4-y3, 2)+Math.pow(x4-x3, 2); double c4=Math.pow(y1-y4, 2)+Math.pow(x1-x4, 2); if(c1==c2&&c2==c3&&c3==c4) System.out.print(true+" "); else System.out.print(false+" "); if(K(x1,y1,x2,y2,x3,y3,x4,y4)==0&&c1==c3&&isvertical(x1,y1,x4,y4,x4,y4,x3,y3)==1) System.out.print(true+" "); else System.out.print(false+" "); if(c1==c2&&c2==c3&&c3==c4&&isvertical(x1,y1,x4,y4,x4,y4,x3,y3)==1) System.out.print(true); else System.out.print(false); } else System.out.print("not a quadrilateral");
选项3:判断是凹四边形(false)还是凸四边形(true),输出四边形周长、面积,结果之间以一个英文空格符分隔
if(K(x1,y1,x2,y2,x2,y2,x3,y3)==1&&K(x2,y2,x3,y3,x3,y3,x4,y4)==1&&K(x3,y3,x4,y4,x1,y1,x4,y4)==1&&flag2==1&&flag3==1) { System.out.print(concave_convex(x1,y1,x2,y2,x3,y3,x4,y4)+" "); double C,S1,S2,p1,p2,p3,p4; double len1=Math.sqrt(Math.pow(x1-x2, 2)+Math.pow(y1-y2, 2)); double len2=Math.sqrt(Math.pow(x2-x3, 2)+Math.pow(y2-y3, 2)); double len3=Math.sqrt(Math.pow(x3-x4, 2)+Math.pow(y3-y4, 2)); double len4=Math.sqrt(Math.pow(x4-x1, 2)+Math.pow(y4-y1, 2)); double len5=Math.sqrt(Math.pow(x1-x3, 2)+Math.pow(y1-y3, 2)); double len6=Math.sqrt(Math.pow(x2-x4, 2)+Math.pow(y2-y4, 2)); p1=(len1+len2+len5)/2; p2=(len3+len4+len5)/2; p3=(len1+len4+len6)/2; p4=(len3+len2+len6)/2; S1=Math.sqrt(p1*(p1-len1)*(p1-len2)*(p1-len5))+Math.sqrt(p2*(p2-len3)*(p2-len4)*(p2-len5)); S2=Math.sqrt(p3*(p3-len1)*(p3-len4)*(p3-len6))+Math.sqrt(p4*(p4-len2)*(p4-len3)*(p4-len6)); C=len1+len2+len3+len4; prinf(C); System.out.print(" "); if(S1<=S2) prinf(S1); else prinf(S2); } else System.out.print("not a quadrilateral");
选项4:
if(x1==x2&&y1==y2) System.out.println("points coincide"); else { double[] k=new double[5]; int num=0; k[1]=K(m[0],n[0],m[1],n[1],m[1],n[1],m[2],n[2]); k[2]=K(m[1],n[1],m[2],n[2],m[2],n[2],m[3],n[3]); k[3]=K(m[2],n[2],m[3],n[3],m[3],n[3],m[0],n[0]); k[4]=K(m[3],n[3],m[0],n[0],m[0],n[0],m[1],n[1]); for (int j=1;j<5;j++) if(k[j]==0) num++; if(lines_coincidence(x1,y1,x2,y2,m[0],n[0],m[1],n[1])||lines_coincidence(x1,y1,x2,y2,m[1],n[1],m[2],n[2])||lines_coincidence(x1,y1,x2,y2,m[2],n[2],m[3],n[3])||lines_coincidence(x1,y1,x2,y2,m[3],n[3],m[0],n[0])) System.out.println("The line is coincide with one of the lines"); else { if(num==0) { if(isquad(m[0],n[0],m[1],n[1],m[2],n[2],m[3],n[3])==0) System.out.println("not a quadrilateral or triangle"); else { double S0=calculateS(m[0],n[0],m[1],n[1],m[2],n[2],m[3],n[3]); double[] p=new double[4]; double[] q=new double[4]; int G=0,G0; for (int i=0;i<4;i++) { if(K(x1,y1,x2,y2,m[i],n[i],m[(i+1)%4],n[(i+1)%4])==1) { double z1,z2; z1=cross(1,x1,y1,x2,y2,m[i],n[i],m[(i+1)%4],n[(i+1)%4]); z2=cross(2,x1,y1,x2,y2,m[i],n[i],m[(i+1)%4],n[(i+1)%4]); if(z1>=Math.min(m[i],m[(i+1)%4])&&z1<=Math.max(m[i],m[(i+1)%4])&&z2>=Math.min(n[i],n[(i+1)%4])&&z2<=Math.max(n[i],n[(i+1)%4])) { p[G]=z1; q[G]=z2; G++; } } } G0=G; for (int i=0;i<G0;i++) { for (int j=i+1;j<G0;j++) if(p[i]==p[j]&&q[i]==q[j]) G--; } if(G<=1) System.out.print(G); else { double x0=p[0],y0=q[0],xt=0,yt=0; for (int i=0;i<G0;i++) if(x0!=p[i]||y0!=q[i]) { xt=p[i];yt=q[i];break; } if(G0-G==0) { int f=-1; for (int i=0;i<4;i++) if(K(m[i],n[i],x0,y0,x0,y0,m[(i+1)%4],n[(i+1)%4])==0) { f=i; break; } double S=calculateS(m[f],n[f],m[(f+3)%4],n[(f+3)%4],xt,yt,x0,y0); double s0=S0-S; if(S<s0) { double o=S; S=s0; s0=o; } System.out.print(G+" "); prinf(s0); System.out.print(" "); prinf(S); } if(G0-G==1||G0-G==2) { int f=-1; for (int i=0;i<4;i++) if((x0==m[i]&&x0==n[i])||(xt==m[i]&&xt==n[i])) { f=i; break; } double S=calculateS(m[f],n[f],m[(f+3)%4],n[(f+3)%4],xt,yt,x0,y0); double s0=S0-S; if(S<s0) { double o=S; S=s0; s0=o; } System.out.print(G+" "); prinf(s0); System.out.print(" "); prinf(S); } } } } else if(num==1||num==2) { int fg=0,dex=-1; for (int i=0;i<4;i++) { int j=(i+1)%4; if(m[i]==m[j]&&n[i]==n[j]&&K(m[i],n[i],m[(i+1)%4],n[(i+1)%4],m[i],n[i],m[(i+3)%4],n[(i+3)%4])==1) { fg=1; dex=i; break; } } int t=-1; for(int i=0;i<4;i++) { if(T(m[i],n[i],m[(i+1)%4],n[(i+1)%4],m[(i+1)%4],n[(i+1)%4],m[(i+2)%4],n[(i+2)%4])==0) t=0; } if(t==0&&fg==0) System.out.println("not a quadrilateral or triangle"); else { double[] r=new double[3]; double[] u=new double[3]; if(fg==1) { for(int i=0,j=0;i<4;i++) { if(i==dex) continue; r[j]=m[i]; u[j]=n[i]; j++; } } else { dex=0; for(int i=0;i<4;i++) { if(K(m[(i+3)%4],n[(i+3)%4],m[i],n[i],m[i],n[i],m[(i+1)%4],n[(i+1)%4])==0) { dex=i; break; } } for(int i=0,j=0;i<4;i++) { if(i==dex) continue; r[j]=m[i]; u[j]=n[i]; j++; } } double[] p=new double[4]; double[] q=new double[4]; int G=0,G0; for (int i=0;i<3;i++) { if(K(x1,y1,x2,y2,r[i],u[i],r[(i+1)%3],u[(i+1)%3])==1) { double z1,z2; z1=cross(1,x1,y1,x2,y2,r[i],u[i],r[(i+1)%3],u[(i+1)%3]); z2=cross(2,x1,y1,x2,y2,r[i],u[i],r[(i+1)%3],u[(i+1)%3]); if(z1>=Math.min(r[i],r[(i+1)%3])&&z1<=Math.max(r[i],r[(i+1)%3])&&z2>=Math.min(u[i],u[(i+1)%3])&&z2<=Math.max(u[i],u[(i+1)%3])) { p[G]=z1; q[G]=z2; G++; } } } G0=G; for (int i=0;i<G0;i++) { for (int j=i+1;j<G0;j++) if(p[i]==p[j]&&q[i]==q[j]) G--; } if(G<=1) System.out.print(G); else { double S0=der(r[0],u[0],r[1],u[1],r[2],u[2]); double x0=p[0],y0=q[0],xt=0,yt=0; for (int i=0;i<G0;i++) if(x0!=p[i]||y0!=q[i]) { xt=p[i];yt=q[i];break; } if(G0-G==0) { int f=-1; for (int i=0;i<3;i++) if(K(r[i],u[i],x0,y0,x0,y0,r[(i+1)%3],u[(i+1)%3])==0&&K(r[(i+1)%3],u[(i+1)%3],xt,yt,xt,yt,r[(i+2)%3],u[(i+2)%3])==0) { f=i; break; } double S=calculateS(r[f],u[f],r[(f+2)%3],u[(f+2)%3],xt,yt,x0,y0); double s0=S0-S; if(S<s0) { double o=S; S=s0; s0=o; } System.out.print(G+" "); prinf(s0); System.out.print(" "); prinf(S); } if(G0-G==1) { int f=-1; double S=0; for (int i=0;i<3;i++) { if(x0==r[i]&&y0==u[i]) { S=der(r[i],u[i],r[(i+1)%3],u[(i+1)%3],xt,yt); break; } if(xt==r[i]&&yt==u[i]) { S=der(r[i],u[i],r[(i+1)%3],u[(i+1)%3],x0,y0); break; } } double s0=S0-S; if(S<s0) { double o=S; S=s0; s0=o; } System.out.print(G+" "); prinf(s0); System.out.print(" "); prinf(S); } } } } else System.out.println("not a quadrilateral or triangle"); } } } }
选项4所用函数:判断点的位置
根据线性代数的知识计算交点坐标
double a1 = y2- y1; double b1 = x1 - x2; double c1 = x1*y2 - x2*y1; double a2 = y4 - y3; double b2 = x3 - x4; double c2 = x3*y4 - x4*y3; double det= a1*b2 - a2*b1; double x0 = (c1*b2 - c2*b1)/det; double y0 = (a1*c2 - a2*c1)/det; if((x0==x1&&y0==y1)||(x0==x2&&y0==y2)||(x0==x3&&y0==y3)||(x0==x4&&y0==y4)) { System.out.println(x0+","+y0+" "+"false"); }
从网上学习的判断交点是否在线段内的函数用法 else if(!java.awt.geom.Line2D.linesIntersect(x1, y1, x2, y2, x3, y3, x4, y4)) { if(x1==Math.max(Math.max(x2, x3),Math.max(x2, x4))||x1==Math.min(Math.min(x2, x3),Math.min(x2, x4))) System.out.println(x0+","+y0+" "+"false"); else System.out.println(x0+","+y0+" "+"true"); } else { System.out.println(x0+","+y0+" "+"true");
选项5:判断点的位置
double[] k=new double[5]; int num=0; k[1]=K(m[0],n[0],m[1],n[1],m[1],n[1],m[2],n[2]); k[2]=K(m[1],n[1],m[2],n[2],m[2],n[2],m[3],n[3]); k[3]=K(m[2],n[2],m[3],n[3],m[3],n[3],m[0],n[0]); k[4]=K(m[3],n[3],m[0],n[0],m[0],n[0],m[1],n[1]); //k[5]=K(m[2],n[2],m[0],n[0],m[0],n[0],m[1],n[1]); for (int j=1;j<5;j++) if(k[j]==0) { num++; } if(num==0) { if(isquad(m[0],n[0],m[1],n[1],m[2],n[2],m[3],n[3])==0) System.out.println("not a quadrilateral or triangle"); else { int on=0; for (int i=0;i<4;i++) if(onorout(x,y,m[i],n[i],m[(i+1)%4],n[(i+1)%4])==1) on=1; if(on==1) System.out.println("on the quadrilateral"); else { double sum=0; for (int i=0;i<4;i++) { double sum0=der(x,y,m[i],n[i],m[(i+1)%4],n[(i+1)%4]); sum=sum+sum0; } double S=calculateS(m[0],n[0],m[1],n[1],m[2],n[2],m[3],m[3]); if(S==sum) System.out.println("in the quadrilateral"); else System.out.println("outof the quadrilateral"); } } } else if(num==1||num==2) { int fg=0,dex=-1; for (int i=0;i<4;i++) { for (int j=i+1;j<4;j++) if(m[i]==m[j]&&n[i]==n[j]&&K(m[i],n[i],m[(i+1)%4],n[(i+1)%4],m[i],n[i],m[(i+3)%4],n[(i+3)%4])==1) { fg=1; dex=i; break; } } int t=-1; for(int i=0;i<4;i++) { if(T(m[i],n[i],m[(i+1)%4],n[(i+1)%4],m[i],n[i],m[(i+2)%4],n[(i+2)%4])==0) t=0; } if(t==0&&fg==0) System.out.println("not a quadrilateral or triangle"); else { double[] r=new double[3]; double[] u=new double[3]; if(fg==1) { for(int i=0,j=0;i<4;i++) { if(i==dex) continue; r[j]=m[i]; u[j]=n[i]; j++; } } else { dex=0; for(int i=0;i<4;i++) { if(K(m[(i+3)%4],n[(i+3)%4],m[i],n[i],m[i],n[i],m[(i+1)%4],n[(i+1)%4])==0) { dex=i; break; } } } for(int i=0,j=0;i<4;i++) { if(i==dex) continue; r[j]=m[i]; u[j]=n[i]; j++; } int on=0; for (int i=0;i<3;i++) if(onorout(x,y,r[i],u[i],r[(i+1)%3],u[(i+1)%3])==1) on=1; if(on==1) System.out.println("on the triangle"); else { double sum=0; for (int i=0;i<3;i++) { double sum0=der(x,y,r[i],u[i],r[(i+1)%3],u[(i+1)%3]); sum=sum+sum0; } double S=der(r[0],u[0],r[1],u[1],r[2],u[2]); if(S==sum) System.out.println("in the triangle"); else System.out.println("outof the triangle"); } } } else System.out.println("not a quadrilateral or triangle"); } } else System.out.println("Wrong Format"); }
踩坑点:
1.错误的理解了点重叠在选项4中的应用,错误的认为4个点均不能重复,而导致许多测试点无法通过;
2.第一题的格式是否合法在第二题不完全适用,但由于测试点无法给出具体问题所在,而一直无法发现错误;
3.选项4中有关三角形能否构成的条件不是很理解,不能get到跟测试点符合的要求;
改进建议:
由于代码中多次运用Double.parseDouble(a[i])方法,而导致代码复杂度较高,建议将其在代码初始位置就转换完成,而不是每个选项都转换一次。
题目集 7-3 设计一个银行业务类
整体思路分析:
1.这一题考察了对类的创建和使用,总体较为基础。
度量分析
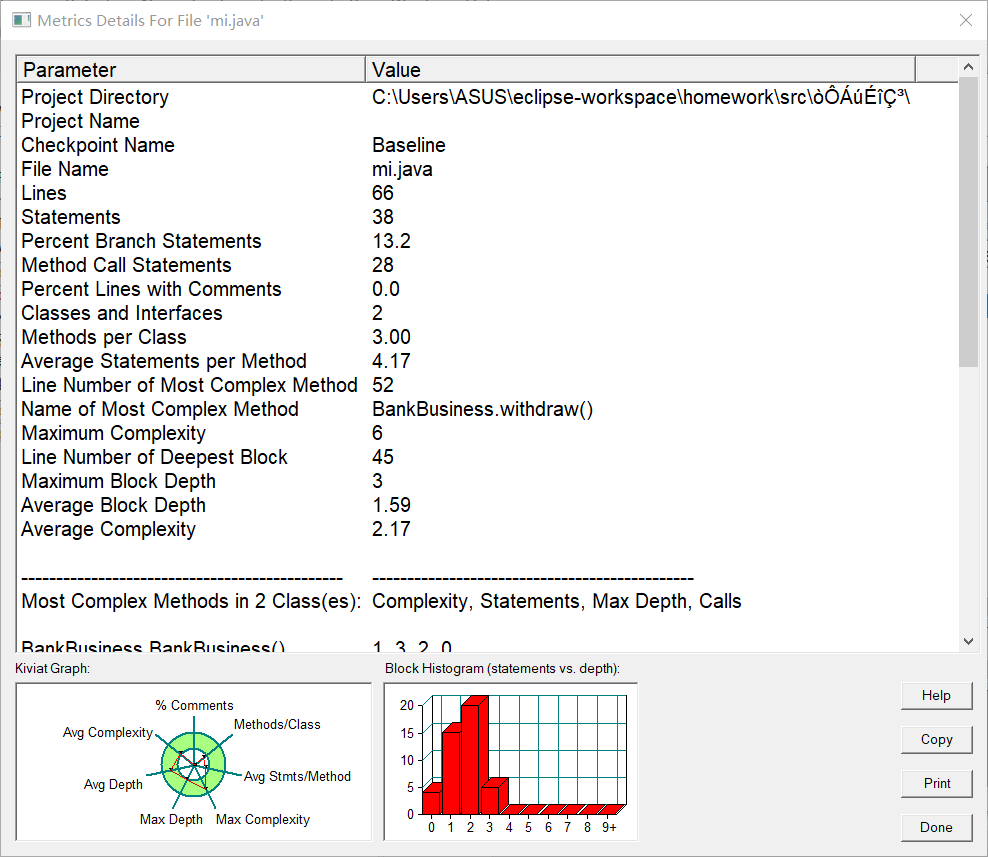
核心代码分析
1.银行类的创建
class BankBusiness { public static String bankname = "中国银行"; private String name,password; private double balance; BankBusiness(String n,String p) { name=n; password=p; balance =0; } public static void welcome() { System.out.println(bankname+"欢迎您的到来!"); } public static void welcomeNext() { System.out.print("请收好您的证件和物品,欢迎您下次光临!"); } public void deposit(String p,double b) { if(p.equals(password)) { balance+=b; System.out.println("您的余额有"+balance+"元。"); } else System.out.println("您的密码错误!"); } public void withdraw(String p,double b) { if(p.equals(password)&&b<=balance) { balance-=b; System.out.println("请取走钞票,您的余额还有"+balance+"元。"); } else if(p.equals(password)&&b>balance) { System.out.println("您的余额不足!"); } else System.out.println("您的密码错误!"); } }
踩坑点:
1.私有数据不能直接访问,需要用set方法进行调用;
2.密码的字符串不能直接比较,需要用equals方法判断密码是否正确。
改进建议:题目要求较简单,无改进建议。
总结
1.对于第四次大作业的编写,除了7-1,7-2还能静下心来减少代码的复杂度,7-3只完全执着于过测试点,而忽略了代码的复杂度问题,最终造成了900行代码的“惨烈壮举”(甚至在写的过程中,由于代码过多而出现无法提交的情况),希望以后能引以为戒,追求结果的同时也不能忽视质量的好坏,将其养成习惯,持之以恒;
2.这次作业和考试让我了解到,光靠上课听老师讲,看老师举例子,去理解,是完全不够的,必须需要自己勤加练习,经过这考试,我发现自己对列表和抽象类的使用有很多不熟悉和了解的地方,需要多看书,多敲代码,才能弥补这方面的不足;
3.这次作业唯一的缺陷还是类的建立和使用太少,一是不够熟练,二是类的建立可能会大幅度减少我的代码行数和复杂度;
4.这次大作业让我意识到,难度较高的代码如果出现错误,很难凭借眼力找出,这时,debug的重要性就显现了,通过debug,大幅度减少了我找bug的时间,所以,掌握每门语言、每种软件的debug技巧十分重要;
5.通过这次考试和作业,我更加体会到类的使用以及继承与多肽的使用带来的便利,非常值得学习;
6.希望老师能够多出一些继承与类的题目,而不是一些复杂的数学题,更希望自己能练习一些上课学的知识的题目。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号