【算法】【动态规划】背包问题

0-1背包

题目链接：https://www.acwing.com/problem/content/2/

思路

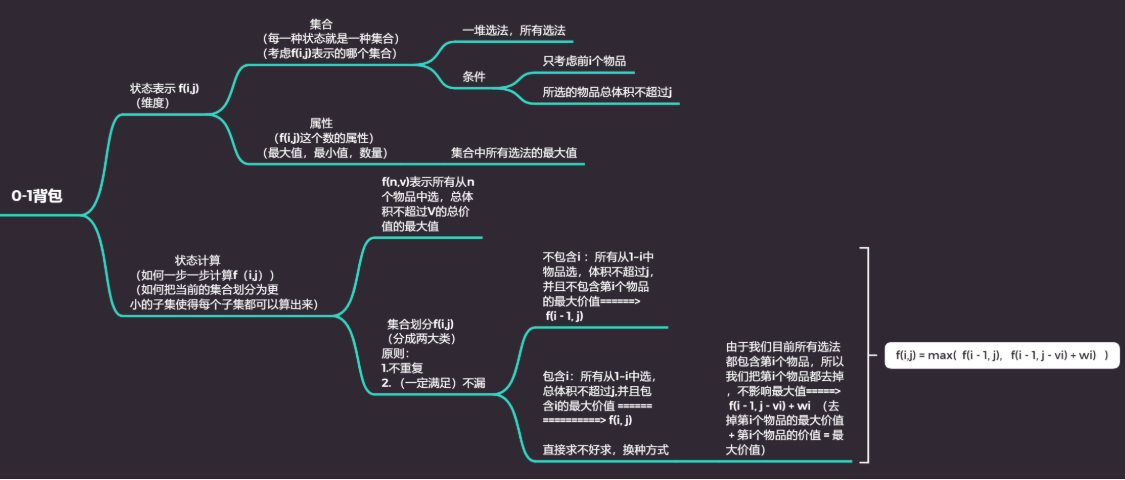
实现

#include <iostream>

using namespace std;

const int N = 1010;
int dp[N][N];
int V[N];
int W[N];

int main()
{
    int n, v;
    cin >> n >> v;
    for(int i = 1; i <= n; i++)
    {
        cin >> V[i] >> W[i];
    }
    
    
    for(int i = 1 ; i <= n; i++)
    {
        for(int j = 1; j <= v; j++)
        {
            dp[i][j] = dp[i - 1][j];
            if(j - V[i] >= 0) dp[i][j] = max(dp[i][j], dp[i - 1][j - V[i]] + W[i]);
        }
    }
    cout << dp[n][v] << endl;
}

完全背包

题目链接：https://www.acwing.com/problem/content/3/

思路

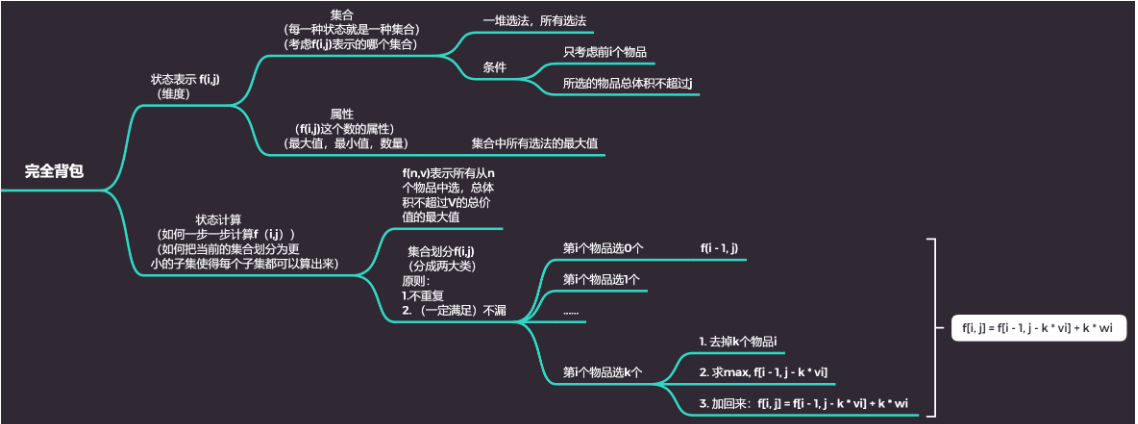
实现

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N]; //每个物品的体积  价值
int dp[N][N];//状态
int main()
{
    cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int  j = 1; j <= m; j++)
            for(int k = 0; v[i] * k <= j; k++)
                dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i] * k] + w[i] * k);

    cout << dp[n][m] << endl;
    return 0;
}

分割等和子集

题目链接：https://leetcode-cn.com/problems/partition-equal-subset-sum/