【排序】各种排序算法
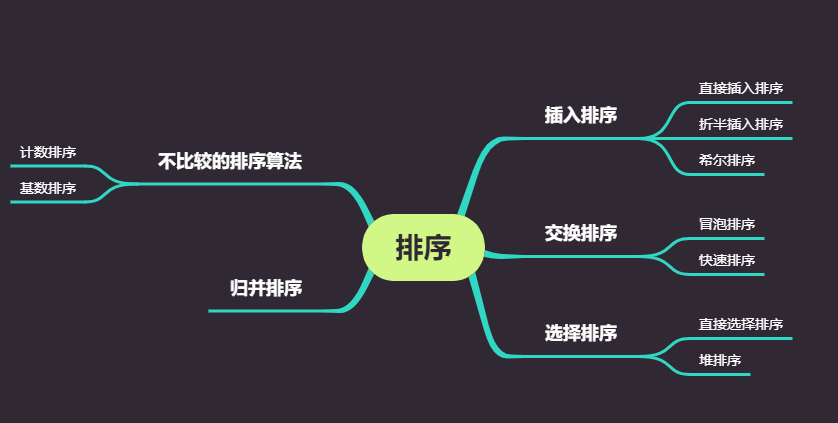
插入排序
每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子表中适当位置,直到全部记录插入完成为止;
直接插入排序
思想
- 待排序的记录放在数组R[0, n - 1]中;
- 排序过程中将R分成两个子区间,有序区R[0, i-1], 无序区R[i, n - 1];
- 将当前无序区的第1个记录,插入到有序区中适当的位置上;
每次是有序区增加一个记录,知道插入完毕为止
复杂度分析
O(n^2) 稳定排序
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void insert_sort(int a[], int n)
{
for(int i = 1; i < n; i++)
{
int tmp = a[i]; //无序区第一个元素
int j = i - 1;
//将无序区的第一个元素插入到有序区合适的位置
while(j >=0 && tmp < a[j]) a[j + 1] = a[j], j--;
a[j + 1] = tmp;
}
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
insert_sort(a, n);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
折半插入排序
复杂度分析
O(n^2) 非稳定排序
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void mid_insert_sort(int a[], int n)
{
for(int i = 1; i < n; i++)
{
int tmp = a[i]; //无序区第一个元素
int l = 0, r = i - 1;
//使用二分确定要插入的位置
while(l <= r)
{
int mid = (l + r) >> 1;
if(tmp < a[mid]) r = mid - 1;
else l = mid + 1;
}
//顺序移动进行插入
for(int j = i - 1; j >= r + 1; j--)
a[j + 1] = a[j];
a[r + 1] = tmp;
}
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
mid_insert_sort(a, n);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
希尔排序
思想
- 取一个小于n的整数d1作为第一个增量,将数组分成d1个组,索引为d1的倍数的数放在同一个组,在各组内进行直接插入排序
- 取第二个增量d2,重复上述分组和排序,直到dt = 1;所有数在同一组进行直接插入排序为止;
复杂度分析
时间复杂度约为O(n^1.3) 不是稳定排序
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void shell_insert(int a[], int n)
{
int gap = n / 2;
while(gap > 0)
{
//对所有索引相距gap位置的所有元素进行排序
for(int i = gap; i < n; i++)
{
int tmp = a[i];
int j = i - gap;
while(j >= 0 && tmp < a[j])
{
a[j + gap] = a[j];
j = j - gap;
}
a[j + gap] = tmp;
j -= gap;
}
gap /= 2;
}
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
shell_insert(a, n);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
交换排序
两两比较待排序记录的关键字,发现两个记录的次序相反时即进行交换,直到没有反序的记录为止;
冒泡排序
思想
通过数组相邻两个数间的比较和为止的交换,使得关键字最小的记录如气泡一样之间冒出水面
n个元素排序,n-1趟冒泡
复杂度分析
时间复杂度O(n^2) 稳定
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void bubble_sort(int a[], int n)
{
for(int i = 0; i < n - 1; i++)
{
for(int j = n - 1; j > i; j--)
if(a[j] < a[j - 1]) swap(a[j], a[j - 1]);
}
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
bubble_sort(a, n);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
快速排序
思想
- 在待排序的n个记录中任取一个记录(通常去第一个记录)作为基准
- 把该记录放入适当位置,数据序列被此记录划分为两部分,分别是比基准小和比基准大的记录。
- 对基准两边的序列用同样的策略进行操作
复杂度分析
时间复杂度O(nlogn) 空间复杂度O(logn) 非稳定
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void quick_sort(int a[], int l, int r)
{
if(l >= r) return;
int i = l - 1, j = r + 1, x = a[l + r >> 1];
while(i < j)
{
do i++; while(a[i] < x);
do j--; while(a[j] > x);
if(i < j) swap(a[i], a[j]);
}
quick_sort(a, l, j);
quick_sort(a, j + 1, r);
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
quick_sort(a, 0, n - 1);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
选择排序
每一次从待排序的记录中选出关键字最小的记录,顺序放在已排好序的数组的最后,直到全部排完;
直接选择排序
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void select_sort(int a[], int n)
{
for(int i = 0; i < n - 1; i++)
{
int k = i; //无序区的起始位置
//选择无序区中最小的数
for(int j = i + 1; j < n; j ++)
if(a[j] < a[k]) k = j;
//将最小的数交换到无序区开始
if(k != i) swap(a[i], a[k]);
}
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
select_sort(a, n);
for(int i = 0; i < n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
堆排序
思想
利用二叉树的顺序存储,将数组看成是二叉树;编号为i的节点的左孩子节点的编号为2i,右孩子节点的编号为2i+1;
小根堆:根节点小于等于左右节点
大根堆:根节点大于等于左右节点
排序的过程中,将数组看成是一颗完全二叉树,利用完全二叉树中双亲节点和孩子节点之间的内在关系,在当前无序区中选择关键字最大或最小的数;
核心:
构建大根堆,以节点i为根,左右子树为堆,将i的左右孩子中比大的与其进行交换,进行up操作
构建小根堆,以节点i为根,左右子树为堆,将i的左右孩子中比小的与其进行交换,进行down操作
复杂度分析
时间复杂度为O(nlogn)
#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
void down(int a[], int u, int n)
{
int t = u;
//找到u的左右节点中比它小的节点
if(u * 2 <= n && a[u * 2] < a[t]) t = u * 2;
if(u * 2 + 1 <= n && a[u * 2 + 1] < a[t]) t = u * 2 + 1;
if(u != t)
{
//交换两个节点
swap(a[u], a[t]);
//对
down(a, t, n);
}
}
int main()
{
int n;
cin>>n;
for(int i = 1; i <= n; i++)
cin>>a[i];
for(int i = n / 2; i; i--)
down(a, i, n);
int m = n;
while(m--)
{
cout<<a[1]<<" ";
a[1] = a[n];
n--;
down(a, 1, n);
}
cout<<endl;
}
归并排序
思想
多次将两个或两个以上的有序表合并成一个新的有序表
复杂度分析
时间复杂度O(nlogn) 空间复杂度O(n)
#include <iostream>
using namespace std;
const int N = 100010;
int a[N], tmp[N];
void merge_sort(int a[], int l, int r)
{
if(l >= r) return ;
int mid = (l + r) >> 1, i = l, j = mid + 1;;
merge_sort(a, l, mid);
merge_sort(a, mid + 1, r);
int k = 0;
while(i <= mid && j <= r)
{
if(a[i] < a[j]) tmp[k++] = a[i++];
else tmp[k++] = a[j++];
}
while(i <= mid) tmp[k++] = a[i++];
while(j <= r) tmp[k++] = a[j++];
for(int i = l, j = 0; i <= r; i++, j++) a[i] = tmp[j];
}
int main()
{
int n;
cin>>n;
for(int i = 0; i < n; i++)
cin>>a[i];
merge_sort(a, 0, n - 1);
for(int i = 0; i< n; i++)
cout<<a[i]<<" ";
cout<<endl;
}
不比较的排序算法
计数排序
思想
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 根据C[i]的值,整理排序结果
复杂度分析
时间复杂度O(n + MaxNum) 空间复杂度一般较高
适合于关键字数值密集的场合中
基数排序
思想
通过“分配”和“收集”来实现排序,借助多关键字排序的思想对单关键字排序
- 先按照最低位的值对记录进行分配、收集;
- 在前一趟的基础上,在对高位的值分配和收集,直至最高位,则完成了基数排序的整个过程
复杂度分析
时间复杂度O(d(n + r)) 分配O(n) 收集O(r) 分配-收集d趟
总结
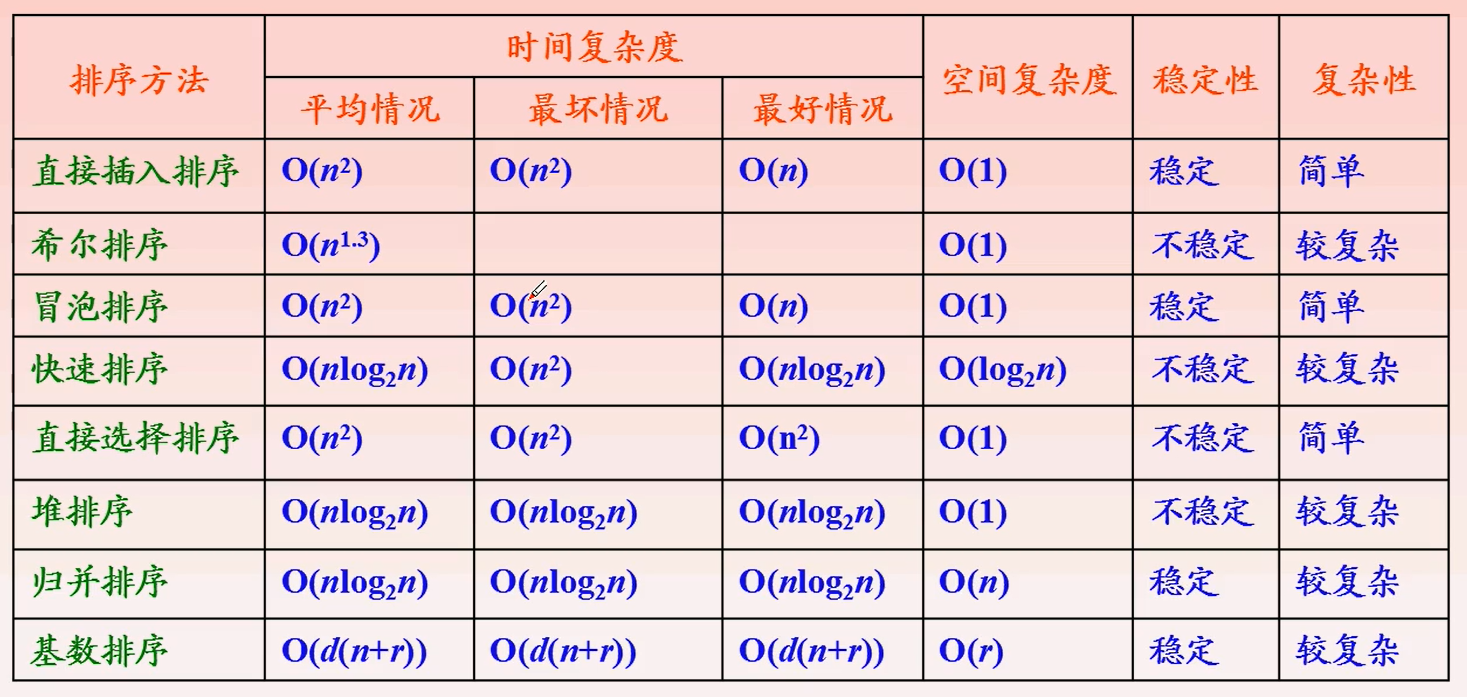
- 若n较小(小于50),直接插入排序和直接选择不错
- 数据基本有序,选用直接插入、冒泡、随机的快速排序;
- n较大,用O(nlogn)的算法
1) 快速排序当关键字的随机分布好时用
2) 堆排序空间复杂度好,且不会出现快速排序的最坏情况
3) 归并排序是稳定算法 - 基数排序可能在O(n)内完成,单关键字类型受限
知识的价值不在于占有,而在于使用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号