【剑指offer】【数学】62.圆圈中最后剩下的数字

题目链接：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/

思路

1. 只关心最终活着的那个人的序号变化，从编号（索引值）的角度考虑；
   
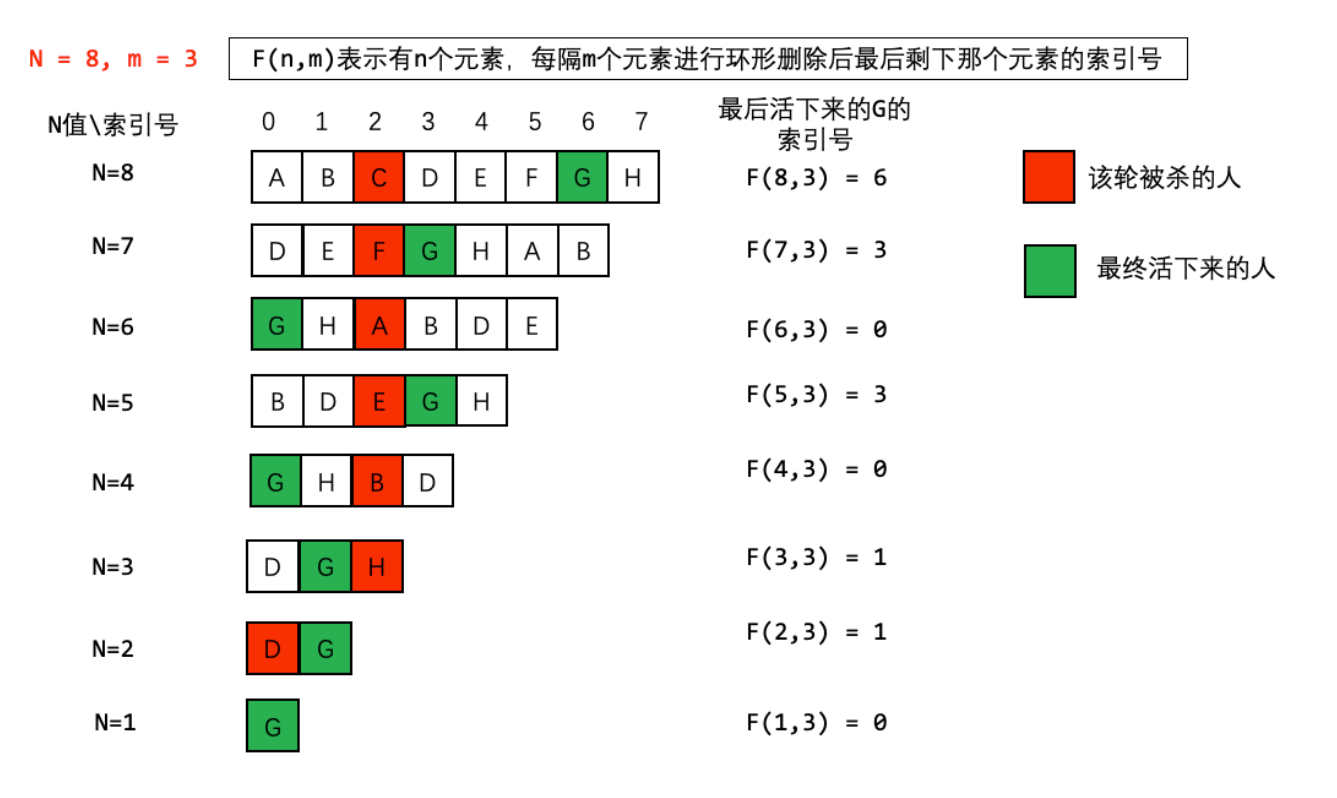
   从8个人开始，每次杀一个人，去掉被杀的人，然后把杀掉的那个人之后的第一个人作为开头重新编号；
   当只剩下一个人的时候，它的编号必定为0；
2. 反推（回退）
   从N = 7反推到N = 8
   
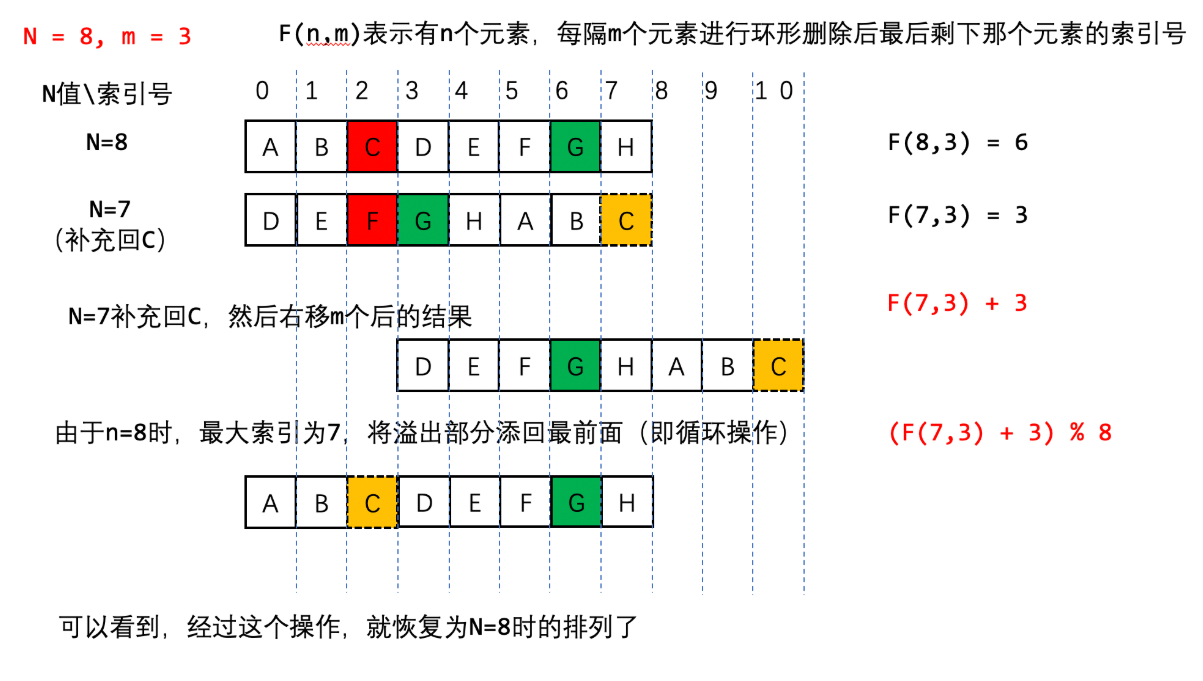
   因此我们可以推出递推公式f(8,3) = [f(7, 3) + 3] % 8
   进行推广泛化，即f(n,m) = [f(n-1, m) + m] % n;

递归

时间复杂度：O(n)
空间复杂度：O(n): 递归深度为n,需要使用O(n)的栈空间

class Solution {
public:
    int lastRemaining(int n, int m) {
        if(n == 1) return 0;
        return (lastRemaining(n - 1, m) + m) % n;
    }
};

迭代

时间复杂度：O(n)
空间复杂度：O(1)

class Solution {
public:
    int lastRemaining(int n, int m) {
        int ans = 0;
        for(int i = 2; i <= n; i++)
            ans = (ans + m) % i;
        return ans;
    }
};

动态规划

换种方法去想这个问题，找递推公式；
f[n][m]还是表示n个人每次淘汰第m号，最后剩下的人的编号；

f[n - 1][m]和f[n][m]有什么关系呢？
第一轮编号 0 1 2 3 …… m …… n - 1;
第二轮编号 去除m后

旧编号	0	1	……	m - 1	m	……	n
新编号				删除	0	……

也就是说 新编号 = (m + 旧编号) % n
即 f[n][m] = (m + f[n - 1][m]) % n;

初始状态的考虑，当n = 1的时候 f = 1；

参考：https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/solution/huan-ge-jiao-du-ju-li-jie-jue-yue-se-fu-huan-by-as/