CCCC团体程序设计天梯赛 L2-013 红色警报

记录天梯赛题目合集 跳转查看

题目链接

题目描述

战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序，当失去一个城市导致国家被分裂为多个无法连通的区域时，就发出红色警报。注意：若该国本来就不完全连通，是分裂的k个区域，而失去一个城市并不改变其他城市之间的连通性，则不要发出警报。

输入格式：
输入在第一行给出两个整数N（0 < N ≤ 500）和M（≤ 5000），分别为城市个数（于是默认城市从0到N-1编号）和连接两城市的通路条数。随后M行，每行给出一条通路所连接的两个城市的编号，其间以1个空格分隔。在城市信息之后给出被攻占的信息，即一个正整数K和随后的K个被攻占的城市的编号。

注意：输入保证给出的被攻占的城市编号都是合法的且无重复，但并不保证给出的通路没有重复。

输出格式：
对每个被攻占的城市，如果它会改变整个国家的连通性，则输出Red Alert: City k is lost!，其中k是该城市的编号；否则只输出City k is lost.即可。如果该国失去了最后一个城市，则增加一行输出Game Over.。

题目解析

这题的核心的是判断连通性和计算连通块。

判断连通性的方法可以使用DFS跑图。计算连通块同理，用DFS一次跑过的点都是同一个连通块的，用一个数组标记一下，然后继续跑没有标记的点，这样跑了多少次DFS就有多少连通块。

题目中改变整个国家连通性，即是原本同一个连通块的点因为某个点的连边断开后，分属不同的连通块，如下图:

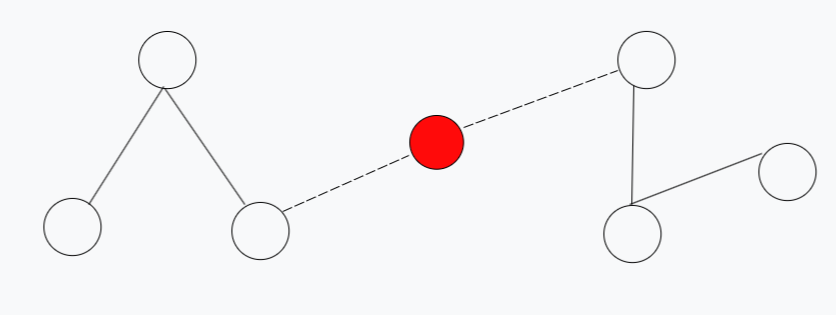
红色点相连的边如果断开，那么左边三个点和右边三个点原本是同一连通块的变为不同的连通块，而且连通块数从原本的1个变为3个，如果红色点不是警报点，它相连的边断开只会让它自己独立，即是连通块多出一个。所以，我们可以通过判断连通块数的变化，来确定红色警报点。

失去所有城市很好判断，看一下k是不是等于所有点数即可，因为题目保证不会重复。

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>

using namespace std;

typedef long long ll;
typedef pair<int, int> PII;

const ll inf = 1e18;
const int INF = 0x3f3f3f3f;
const int N = 1e6 + 10;
const int M = 1000 + 10;

int g[M][M];
bool vis[M];
int num;
int n, m, k;

void dfs(int x)
{
    for (int i = 0; i < n; i ++) 
    	if (!vis[i] && g[x][i]) {
            vis[i] = 1;
            dfs(i);
        }
}

int cal()
{
	int res = 0;
	for (int i = 0; i < n; i ++)
		if (!vis[i]) {
			dfs(i);
			res ++;
		}
	return res;
}

void solve()
{
	cin >> n >> m;

    while (m -- ) {
        int a, b;
        cin >> a >> b;
        g[a][b] = g[b][a] = 1;
    }
    
    num = cal();
    
    cin >> k;
    for (int i = 1; i <= k; i ++) {
        int x;
        cin >> x;
        for (int j = 0; j < n; j ++) 
			if(g[x][j]) g[x][j] = g[j][x] = 0;
        for (int i = 0; i < n; i ++) vis[i] = 0;
        
        int cnt = cal();
        if(cnt >= num + 2) cout << "Red Alert: City " << x << " is lost!\n";
        else cout << "City " << x << " is lost.\n";
        num = cnt;
    }
    if(k == n) cout << "Game Over.";
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	
	int T = 1;
//	cin >> T;
	while (T --) solve();
	return 0;
}