2025牛客寒假算法基础集训营3补题笔记

比赛链接

题目难度顺序大致为：\(A、M、F、L、C、\)

\(easy\)：\(A、M、F、L、C\)

太难了这场。。。E题卡了3个多小时。。。

A.智乃的博弈游戏

题意

有\(n\) 个石头，两人轮流取石头。每次能取小于石头个数且与石头个数互质的数量，当某人取时只有一颗石头则获胜。问先手是否可以必胜。

思路

博弈论，思维

首先，相邻的奇数是互质的，即当 \(n\) 是奇数时，\(n - 2\) 一定和其互质。所以，奇数的局面一定可以留下2个石头给下一个人，而2个石头是必输的局面。
接着考虑当 \(n\) 是偶数时，偶数只能和奇数互质，而偶数-奇数=奇数，留奇数个石头给下一个人，那么下一个人是必胜的，理由如上。
综上所述，先手是奇数个石头必胜，偶数个石头必败。

注意开long long！

时间复杂度： \(O(1)\)

代码

点击查看代码

#include <iostream>

#define ll long long

using namespace std;

ll x;

void solve()
{
    cin >> x;
    if (x % 2) cout << "Yes";
    else cout << "No";
}

int main()
{
  int t = 1;
  while (t --) solve();
  return 0;
}

---

M.智乃的牛题

题意

给一个字符串，询问该字符串的字母能否组成单词 \(nowcoder\)。

思路

模拟
记录每个字母次数，然后查看是否可以拼成 \(nowcoder\) 即可。

时间复杂度：\(O(n)\)

代码

点击查看代码

#include <iostream>
#include <map>

using namespace std;

string s;
map<char, int> mp;
string tmp = "nowcoder";

void solve()
{
    cin >> s;
    for (auto i : s) mp[i] ++;
    for (auto i : tmp)
        if (i == 'o' && mp[i] == 2) continue;
        else if (mp[i] == 1) continue;
        else return void(cout << "I AK IOI");
    cout << "happy new year";
}

int main()
{
    int t = 1;
    while (t --) solve();
    return 0;
}

---

F.智乃的捉迷藏

题意

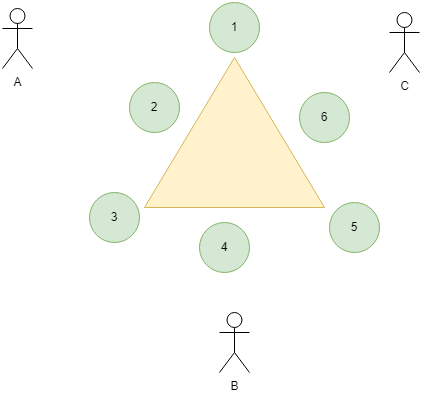
三个人分别可以看见躲藏在面前三个位置上的人，一共有n个人躲藏，询问三人是否可以分别看见\(a、b、c\)个人。
即：\(a = s_1 + s_2 + s_3, b = s_3 + s_4 + s_5, c = s_5 + s_6 + s_1\)

思路

数学
解上面的等式：

\[a + b + c = 2 \times (s_1 + s_3 + s_5) + (s_2 + s_4 + s_6) \\ n = (s_1 + s_3 + s_5) + (s_2 + s_4 + s_6) \\ \]

\[(s_1 + s_3 + s_5) = a + b + c - n \ge 0 \\ (s_2 + s_4 + s_6) = 2n - (a + b + c) \ge 0 \]

\[n \le a + b + c \le 2n \]

时间复杂度：\(O(1)\)

代码

点击查看代码

#include <iostream>

using namespace std;

int n;
int a, b, c;

void solve()
{
  cin >> n >> a >> b >> c;
  if (a + b + c <= 2 * n && a + b + c >= n) cout << "Yes" << '\n';
  else cout << "No" << '\n';
}

int main()
{
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);

  int t = 1;
  cin >> t;
  while (t --) solve();
  return 0;
}

---

L.智乃的三角遍历

题意

给一个 \(n\) 层的三角形，询问是否可以一笔不重不漏的经过三角形上的所有边，如果可以就给出一组序列表示经过的顶点顺序。

思路

模拟

顺序不止一种，自己纸上找到一种规律然后想办法模拟下来就好了。

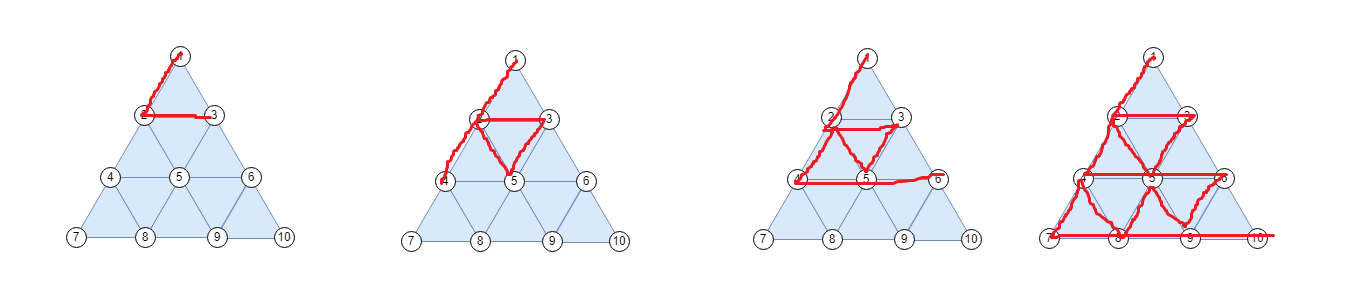
我的顺序是每层画完后接着画下一层

时间复杂度：\(O(n^2)\)

代码

点击查看代码

#include <iostream>
#include <vector>

using namespace std;

const int M = 1000 + 10;

int n, m;
vector<int> g[M];
vector<int> ans;

void solve()
{
    cin >> n;
    
    int num = 1;
    for (int i = 0; i <= n; i ++) {
        int j = i + 1;
        while (j --) g[i].emplace_back(num ++);
    }
    
    cout << "Yes" << '\n';
    for (int i = 0; i <= n; i ++) {
        for (int j = 0; j < g[i].size(); j ++) cout << g[i][j] << ' ';
        if (i + 1 > n) continue;
        for (int j = g[i + 1].size() - 2; j >= 1; j --) 
            cout << g[i + 1][j] << ' ' << g[i][j - 1] << ' ';
    }
    for (int i = n - 1; i >= 0; i --)
        cout << g[i].back() << ' ';
}

int main()
{
  ios::sync_with_stdio(false);
  cin.tie(0), cout.tie(0);

  int t = 1;
  while (t --) solve();
  return 0;
}

---

C.智乃的Notepad(Easy version)

题意

给 \(n\) 个单词，询问最少敲击键盘次数，在使用键盘输入过程中出现所有单词，删除键敲击也算一次。

思路

思维、贪心、字典树、\(dfs\)

存储多个单词，可以想到使用字典树来将所有单词存下。

那么问题就会转换为，遍历这颗字典树上所有节点的最小步数。

可以想到，如果是从根节点出发后再回到根节点，那么所有节点都会遍历两次。而我们并不需要回到根节点，要么从贪心角度出发，我们只需要停留在最深那个节点上即可，这样我们就不要将这最深的路径上的节点又遍历一次，答案为：所有节点个数乘二减去最深的层数。

时间复杂度：\(O(\sum|s_i| \times 26)\)

代码

点击查看代码

#include <iostream>

#define ll long long
#define si(x) int(x.size())

using namespace std;

const int N = 1e6 + 10;
const int M = 30;

int n, m;
int son[N][M], idx;
ll maxv;

void insert(string s)
{
    int p = 0;
    for (int i = 0; i < si(s); i ++) {
        int u = s[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
}

ll dfs(int u, ll stp)
{
    ll res = 1;
    maxv = max(maxv, stp);
    if (u == 0) res = 0;
    for (char i = 'a'; i <= 'z'; i ++) {
        int v = i - 'a';
        if (!son[u][v]) continue;
        ll sum = dfs(son[u][v], stp + 1);
        res += sum;
    }
    return res;
}

void solve()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++) {
        string s;
        cin >> s;
        insert(s);
    }
    int l, r;
    cin >> l >> r;

    int ans = dfs(0, 0);
    cout << ans * 2ll - maxv;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);

    int t = 1;
    while (t --) solve();
    return 0;
}

---

E.智乃的小球

题意

给 \(n\) 个小球，以及每个小球的位置 \(p_i\) 和方向 \(v_i\) ，求第 \(k\) 对完全弹性碰撞在什么时刻发生。

思路

二分、双指针

首先，假设在时刻 \(x\) 时发生了 \(k\) 对完全弹性碰撞，那么在大于 \(x\) 的时刻肯定发生了不小于 \(k\) 对的完全弹性碰撞，在小于 \(x\) 的时刻肯定没有达到 \(k\) 对完全弹性碰撞，所以时刻是具备二分性的，考虑用二分来解决。

接着，就是判断二分的时刻下发生了多少对完全弹性碰撞。
在此之前，还要知道一个点，就是两个小球完全弹性碰撞，可以看成两个小球交错而过。
假设现在向右的小球的位置为：2 4 6 8，向左的小球的位置为：3 5 7，模拟小球运动：当 2 与 3 5两个小球交错而过（即发生了两次完全弹性碰撞，后面的也如此）那么肯定的，4 在此之前一定已经和 5 相遇了一次，现在我们二分了一个时刻，可以预知向右的小球在 \(x\) 时刻后会在 \(p_i + x\) 的位置上，那么在 \([p_i, p_i + x]\) 区间内的向左的小球都会相遇一次，由此我们可以统计出所有向右的小球的碰撞总次数，再和 \(k\) 进行比较。

再计算 \([p_i, p_i + x]\) 区间内的相遇次数时，不能暴力枚举所有向右的小球，可以使用双指针去检测区间内的向左的小球的左右下标。

代码

点击查看代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <iomanip>

using namespace std;

typedef long long ll;

int n, k;
vector<int> u, v;

bool check(ll x)
{
    ll res = 0;
    int l = 0, r = 0;
    for (auto i : u) {
        while (l < v.size() && v[l] < i) l ++;
        while (r < v.size() && v[r] <= i + x) r ++;
        res += r - l;
    }
    return res >= k;
}

int main()
{
    cin >> n >> k;
    for (int i = 0; i < n; i ++) {
        int p, y;
        cin >> p >> y;
        if (y == 1) u.emplace_back(p);
        else  v.emplace_back(p);
    }
    
    sort(u.begin(), u.end());
    sort(v.begin(), v.end());
    
    ll l = 1, r = 1e9;
    while (l < r) {
        ll mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    if (!check(l)) cout << "No";
    else cout << "Yes" << '\n' << fixed << setprecision(6) << 1.0 * l / 2;
    
    return 0;
}

---

J.智乃画二叉树

题意

根据题目数据画二叉树。

思路

超级大模拟，不会。。。

代码

略

---

K.智乃的逆序数

题意

构造一个序列包含若干个值域互不相交子序列，且逆序对恰好为 \(K\) 对。

思路

求逆序数的方法有：冒泡排序、归并排序、树状数组、线段树等。

先简单化考虑，因为给出的是几段大小连续且重排的序列，那么先得出逆序数最少和逆序数最多的情况。
逆序数最少的情况就是每段从小到大进行段间排序，逆序数为每段内的逆序数之和。
最大的情况就是每段从大到小进行段间排序，逆序数要根据冒泡排序算出。

我们可以从最少的逆序数的情况开始构造，如果逆序数量不够，就在段间把各自两个元素进行位置交换，知道逆序数达到 \(k\) 对。

代码

点击查看代码

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;

int n, k;
vector<PII> a;

int main()
{
    cin >> n >> k;
    vector<vector<int>> b(n);
    
    for (int i = 0; i < n; i ++) {
        int l;
        cin >> l;
        for (int j = 0; j < l; j ++) {
            int x;
            cin >> x;
            b[i].emplace_back(x);
        }
    }
    
    sort(b.begin(), b.end(), [](vector<int> a, vector<int> b){
        return a[0] < b[0];
    });
    
    for (int i = 0; i < n; i ++) 
        for (int j : b[i])
            a.emplace_back(i, j);
    
    int sum = 0;
    for (int i = 0; i < a.size(); i ++) 
        for (int j = i + 1; j < a.size(); j ++)
            if (a[i] > a[j]) sum ++;
    
    if (k < sum) return cout << "No", 0;
    k -= sum;
    
    auto print = [&]() -> void {
        cout << "Yes" << '\n';
        for (auto it : a)
            cout << it.second << ' ';
    };
    
    if (k == 0) print();
    else {
        for (int i = 0; i < a.size() - 1; i ++)
            for (int j = 0; j < a.size() - 1 - i; j ++)
                if (a[j].first == a[j + 1].first) continue;
                else if (k && a[j].second < a[j + 1].second) {
                    swap(a[j], a[j + 1]);
                    k --;
                }
        if (k) cout << "No";
        else print();
    }
    
    return 0;
}