[CSP-S 2024] 超速检测 题解
[CSP-S 2024] 超速检测 题解
写在前头的话
这道题是一道很好的物理题,有效地巩固了必修一的知识。
但这道题没有想象中的好做,请看VCR洛谷图床:
题目大意
给定一条长度为 $L$ 的道路,上有 $N$ 个测速点和 $M$ 个摄像头。每个测速点有位置 $d_i$、初始速度 $v_i$ 和加速度 $a_i$。车辆在通过测速点后做匀变速直线运动。当车辆速度超过限速 $V$ 时,会被摄像头记录(记录第一个和最后一个拍到超速的摄像头之间所有摄像头)。求:
-
有超速行为且没有被其他测速点完全覆盖(隐藏)的测速点数量
-
没有被任何超速行为使用的摄像头数量
物理公式
事实上在这题我们会用到的运动学公式有且仅有 $2ax=V_t2-V_02$,如果你使用了太多其它公式进而使用了大量浮点数除法和开根,那么恭喜你由于精度问题会 $WA$ 上几个点。
什么你不会物理?(逃~)
题意分析
注意到 $N$ 和 $M$ 最大可达 $1e5$,这启迪我们思考一个 $O(NlogN)$ 的做法。
又因为这是 $CSP-S$ 组的第二题,那么可使用的方法就那么几个:排序、二分、log级数据结构……
这道题我们选用排序+二分+贪心的组合来解决此题。
具体问题具体分析,我们可以分五步走:
判断每个测速点是否超速
计算超速区间
找到对应覆盖的摄像头
处理隐藏的测速点(去重)
计算答案
判断每个测速点是否超速
这个简单,给你看一张图就明白了:
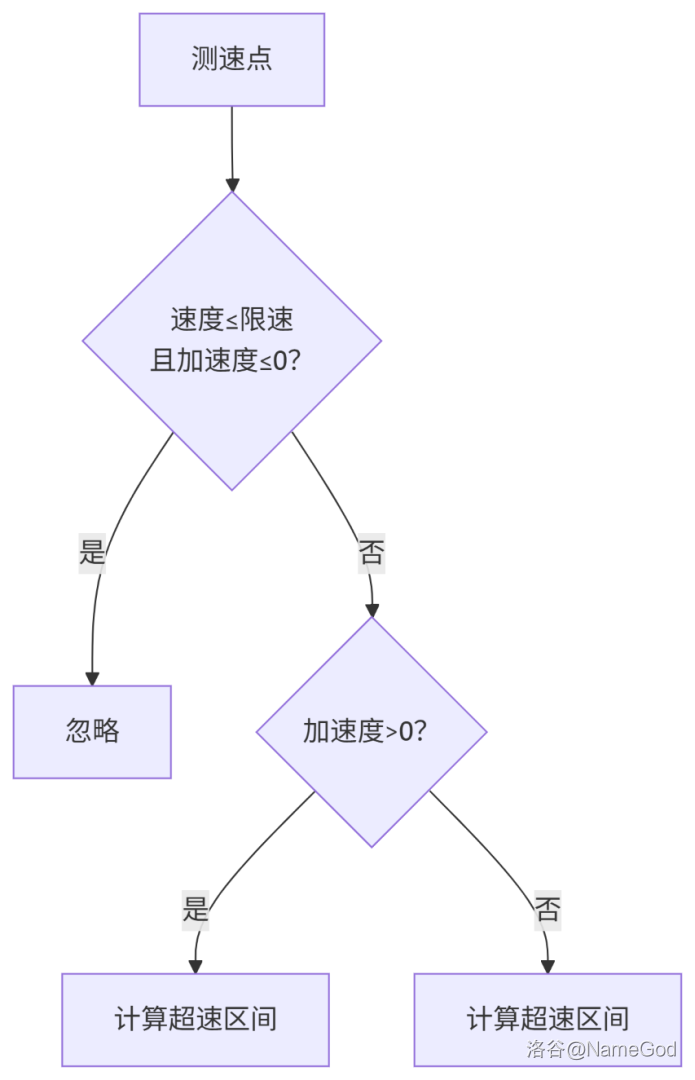
计算超速区间
回想一下你解物理题,从抽象的题干中抽象出抽象的模型,这是一个很抽象的过程。
这道 $OI$ 物理题也大差不差,学习解物理题的经验,我们考虑分类讨论:
根据加速度 $a$ 的正负性分类:
- 加速车(加速度 $a>0$):
如果起点就超速, 那么这辆小车车会从测速点开始一直超速到终点。
如果起点没超速,直接套公式计算从起点加速到限速的位置。
公式: $S=T+(V2-v_02)÷(2×a)$
其中 $S$ 为超速起点,$T$ 为测速点位置,$V$ 为限速,$v_0$ 为起点速度,$a$ 为加速度。
- 减速车(加速度 $a≤0$):
很显然在起点速度 $≤$ 限速时,减速只会越减越小,好比是喝水时别人推了你一把——水没喝完还呛。
所以我们只在起点速度 $>$ 限速时计算。直接套公式计算从起点减速到限速的位置。
公式: $S=T+(V2-v_02)÷(2×a)$
其中 $S$ 为超速终点,$T$ 为测速点位置,$V$ 为限速,$v_0$ 为起点速度,$a$ 为加速度。
找到对应覆盖的摄像头
说白话叫“找到对应覆盖的摄像头”,说鬼话叫“把超速区间变成摄像头编号区间”。
是不是有点迷糊了?
先把操作呈现给大家:
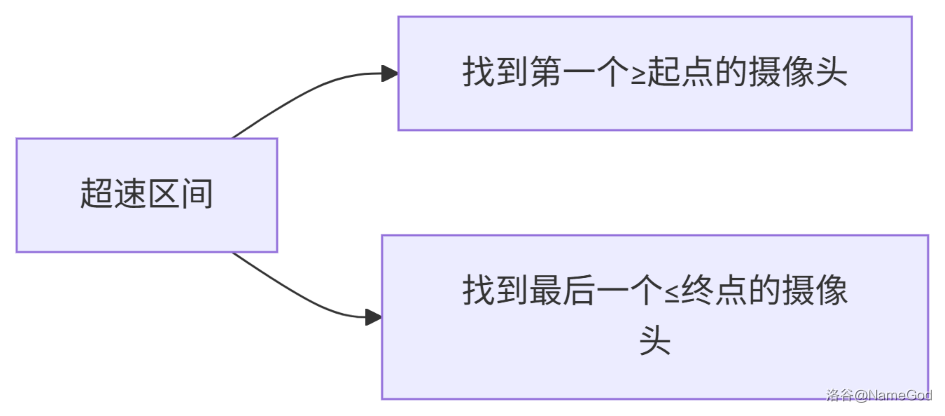
其实这步就是两头夹中间,把找到的抽象区间映射成具体的区间两端摄像头的编号,显然吧,这步(最大的最小 / 最小的最大)很容易联想到二分,给大家附上一个我的二分模板:
int L = 二分确下界, R = 二分确上界, ans = 0;
while (L <= R) {
int mid = (L + R) >> 1;
if (check(mid))// check函数需要具体问题具体分析
ans = mid, R = mid - 1;
else L = mid + 1;
}
// 答案存在ans里
处理隐藏的测速点(去重)
怎么定义“隐藏的测速点”呢?
我们来考虑什么样的区间我们不用单独保留。
显然当一个小区间被完全包含在一个大区间里的时候,这个小区间的占位功能被大区间完全取代。
形式化地,小区间 $[l, r]$,大区间 $[L, R]$,当且仅当 $L≤l≤r≤R$ 时,小区间对答案没有贡献。
这个很直观,妈妈给孩子交好学费了孩子自己就不用再交了嘛。
问题来了,我们怎么统计这样的区间呢?
答案时,把所有区间按起点从小到大排序,从后往前检查:
如果当前区间的终点 $≥$ 后面区间的最小终点 $→$ 当前区间被隐藏
举个例子大家就懂了:
$[1, 10]$ 包含 $[3, 5]$ $→$ $[3, 5]$ 被隐藏
计算答案
重新回到问题,题目要求输出两个答案:
-
有超速行为且没有被其他测速点完全覆盖(隐藏)的测速点数量
-
没有被任何超速行为使用的摄像头数量
那么我们有:
-
未被隐藏的测速点 $=$ 剩余区间数量
-
未使用的摄像头 $=$ 总摄像头数 $-$ 被覆盖的摄像头数
代码
Talk is cheap, show me the code.
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair <int, int> PII;
typedef pair <int, LL> PIL;
typedef pair <LL, int> PLI;
typedef pair <LL, LL> PLL;
inline LL read() {
LL x = 0, f = 1;
char ch = getchar();
while (ch > '9' || ch < '0') {
if (ch == '-')
f = -f;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void write(LL x) {
if (x < 0) {
putchar('-');
x = -x;
}
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
// 小小物理题 不自量力 一眼贪心
const int MAXN = 1e5 + 5;
LL a[MAXN], d[MAXN], v[MAXN], p[MAXN];
bool flag[MAXN];
struct node {
LL l, r; // [l, r]
friend bool operator<(const node &a, const node &b) {
if (a.l != b.l)
return a.l < b.l;
else return a.r > b.r;
}
}s[MAXN];
int main() {
//ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
//freopen("detect.in", "r", stdin);
//freopen("detect.out", "w", stdout);
LL T = read();
while (T--) {
LL N = read(), M = read(), L = read(), V = read(), tot = 0;
for (int i = 1; i <= N; ++i)
d[i] = read(), v[i] = read(), a[i] = read();
for (int i = 1; i <= M; ++i)
p[i] = read();
for (int i = 1; i <= N; ++i) {
// 1: a <= 0 && v <= V
if (a[i] <= 0 && v[i] <= V)
continue;
// 2: a > 0
if (a[i] > 0) {
LL w = (V * V - v[i] * v[i]) / (2 * a[i]) + d[i];
if (v[i] > V)
w = d[i] - 1;
LL l = 1, r = M, ans = 0;
while (l <= r) {
LL mid = (l + r) >> 1;
if (p[mid] > w)
ans = mid, r = mid - 1;
else l = mid + 1;
}
if (!ans)
continue;
s[++tot].l = ans, s[tot].r = M;
}
else {
// a < 0 && v > V
LL l = 1, r = M, pos = 0;
while (l <= r) {
LL mid = (l + r) >> 1;
if (p[mid] >= d[i])
pos = mid, r = mid - 1;
else l = mid + 1;
}
if (!pos)
continue;
l = pos, r = M;
LL ans = 0;
while (l <= r) {
LL mid = (l + r) >> 1;
double su = sqrt(v[i] * v[i] * 1.0 + 2.0 * a[i] * (p[mid] - d[i]));
if (su > V)
ans = mid, l = mid + 1;
else r = mid - 1;
}
if (ans < pos)
continue;
s[++tot].l = pos, s[tot].r = ans;
}
}
sort(s + 1, s + tot + 1);
// 去重
LL minr = LLONG_MAX;
for (int i = tot; i >= 1; --i) {
if (minr <= s[i].r)
flag[i] = 1;
minr = min(minr, s[i].r);
}
LL ans = 0, fu = 0;
for (int i = 1; i <= tot; ++i) {
if (flag[i]) {
flag[i] = 0;
continue;
}
if (fu < s[i].l) {
fu = s[i].r;
ans++;
}
}
write(tot);
putchar(' ');
write(M - ans);
putchar('\n');
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号