无限的路
甜甜从小就喜欢画图画,最近他买了一支智能画笔,由于刚刚接触,所以甜甜只会用它来画直线,于是他就在平面直角坐标系中画出如下的图形:
![]()
甜甜的好朋友蜜蜜发现上面的图还是有点规则的,于是他问甜甜:在你画的图中,我给你两个点,请你算一算连接两点的折线长度(即沿折线走的路线长度)吧。
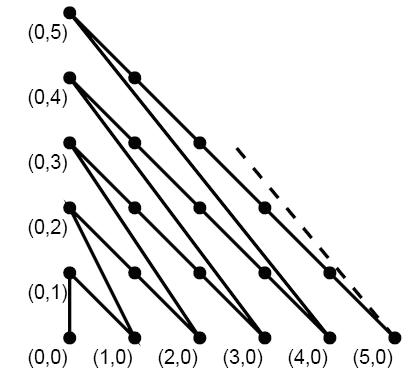
甜甜的好朋友蜜蜜发现上面的图还是有点规则的,于是他问甜甜:在你画的图中,我给你两个点,请你算一算连接两点的折线长度(即沿折线走的路线长度)吧。
Input
第一个数是正整数N(≤100)。代表数据的组数。
每组数据由四个非负整数组成x1,y1,x2,y2;所有的数都不会大于100。
每组数据由四个非负整数组成x1,y1,x2,y2;所有的数都不会大于100。
Output
对于每组数据,输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。
Sample Input
5
0 0 0 1
0 0 1 0
2 3 3 1
99 99 9 9
5 5 5 5
Sample Output
1.000
2.414
10.646
54985.047
0.000
#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
int xian(int &x, int &y)
{
int n,i;
for(i=0;i<=1000;i++)
{
if(y==(-x)+i)
{
n=i;
return n;
break;
}
}
}
int main()
{
int x1,x2,y1,y2,n1,n2,i,t,x11,y11,m,j;
double s1,s2,s3,s;
cin>>m;
for(j=1;j<=m;j++)
{
s1=s2=s3=0;
cin>>x1>>y1>>x2>>y2;
n1=xian(x1,y1);
n2=xian(x2,y2);
if(n1>n2)
{
t=n1;n1=n2;n2=t;
x11=x1;x1=x2;x2=x11;
y11=y1;y1=y2;y2=y11;
}
if(n1==n2) s=pow(pow(x1-x2,2)+pow(y1-y2,2),0.5);
else
{
for(i=n1+1;i<n2;i++)
{
s1+=pow(2,0.5)*i;
}
for(i=n1;i<n2;i++)
{
s2+=pow(i*i+(i+1)*(i+1),0.5);
}
s3=pow((x1-n1)*(x1-n1)+y1*y1,0.5)+pow(x2*x2+(y2-n2)*(y2-n2),0.5);
s=s1+s2+s3;
}
cout<<setiosflags(ios::fixed)<<setprecision(3)<<s<<endl;
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号