2023-07-08 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(五).md
2023-07-08 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(五)
考虑无约束最优化问题
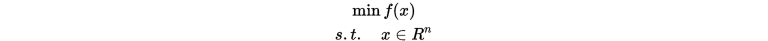
其中
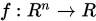 是一阶连续可微的 (记作
是一阶连续可微的 (记作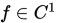 ), 也就具有连续的一阶偏导数. 最速下降法的基本思想正如其名字一样,就是在当前迭代点
), 也就具有连续的一阶偏导数. 最速下降法的基本思想正如其名字一样,就是在当前迭代点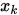 处寻找一个使目标函数下降最快的方向. 这样的方向由下述问题(下降量)
处寻找一个使目标函数下降最快的方向. 这样的方向由下述问题(下降量)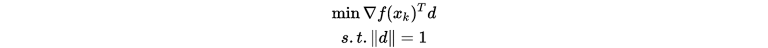
的解
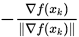 给出,因此
给出,因此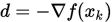 为函数
为函数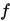 在
在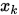 处的最速下降方向。
处的最速下降方向。
最速下降法
Step 1. 选取初始点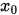 , 给定精度
, 给定精度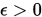 , 置
, 置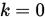 .
.
Step 2. 计算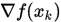 , 若
, 若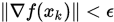 , 则停止,置最优解为
, 则停止,置最优解为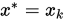 , 否则转下步.
, 否则转下步.
Step 3. 取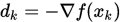 , 作精确线搜索
, 作精确线搜索
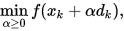
得解
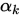 , 令
, 令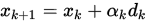 ,
, 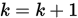 , 转 Step 1.
, 转 Step 1.
下面给出最速下降法的收敛性证明:
定理1 设函数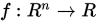 二阶连续可微有下界,存在
二阶连续可微有下界,存在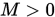 满足
满足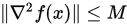 , 若最速下降法产生无穷点列
, 若最速下降法产生无穷点列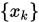 , 则
, 则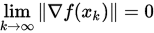 .#673AB7
.#673AB7
证明:由算法和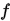 定义可知序列
定义可知序列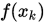 单调有界,即
单调有界,即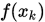 收敛. 对任意
收敛. 对任意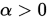 , 存在
, 存在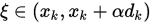 , 使得
, 使得
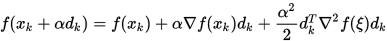
由假设和
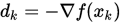 可得
可得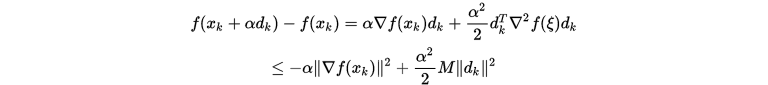
考虑合并
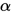 ,得到
,得到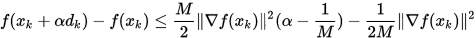
令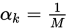 , 由精确线搜索可知
, 由精确线搜索可知
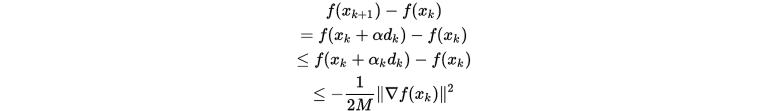
由于
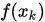 收敛,因此
收敛,因此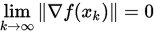 .
.
最速下降法迭代路径呈锯齿状的原因: 由于采用的是精确线搜索方法,在当前下降方向已经充分下降了。从这也可以知道如果是一维优化问题,最速下降法一步即可达到最优 (精确线搜索).
下面的程序可求解多维优化问题,使用的是成功-失败法搜索
- % 最速下降法
- function [x xlog] = SteepestDes(f, x0, epsilon)
- % f 目标函数,函数句柄
- % g 梯度函数 函数句柄
- % epsilon 精度要求
- % method 线搜索方法
- k = 0;
- while k <= 1e4
- diff_x = -My_Gradient(f, x0);
- if norm(diff_x) < epsilon
- x = x0;
- xlog(k+1) = norm(diff_x);
- break
- end
- [alpha tx] = SuccFa(f, 1, x0, diff_x, 1, epsilon, 1e4);
- x0 = x0 + alpha * diff_x;
- k = k + 1;
- xlog(k) = norm(diff_x);
- end
- end
- function [alphak xlog] = SuccFa(fun, alpha, x0, diff_x, h, epsil, maxIt)
- k = 0;
- xlog = alpha;
- while k <= maxIt
- alphak = alpha + h;
- if fun(x0 + alphak * diff_x) < fun(x0 + alpha * diff_x)
- h = 2 * h;
- alpha = alphak;
- else
- h = - h / 4;
- end
- k = k + 1;
- xlog(k) = alphak;
- if abs(h) < epsil
- break
- end
- end
- end
- function [x] = F_alpha(alpha)
- x = f(x0 + alpha * diff_x);
- end
- function [gd] = My_Gradient(f, x)
- gd = x;
- epsil = 1e-5;
- d = [-2* epsil, -epsil 0 epsil 2*epsil];
- tx = [x x x x x];
- fx = [0,0,0,0,0];
- for i = 1:length(x)
- tx(i,:) = tx(i,:) + d;
- for h = 1:5
- fx(h) = f(tx(:,h));
- end
- gf = gradient(fx);
- gd(i) = gf(3);
- end
- end
测试程序
- f = @(x) sin(x(1)) + cos(x(2));
- x0 = [1 ,2]';
- epsilon = 1e-8;
- [x xlog] = SteepestDes(f, x0, epsilon)
- f = @(x) sin(x);
- x0 = 1;
- epsilon = 1e-8;
- [x xlog] = SteepestDes(f, x0, epsilon)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号