2023-06-17《计算方法》- 陈丽娟 - 插值法(二).md
2023-06-17《计算方法》- 陈丽娟 - 插值法(二)
一、埃尔米特插值
埃尔米特插值即是找到一个插值函数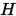 , 使得
, 使得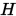 不仅在节点上与原函数值相同,且还要求与原函数在节点处有相同的一阶(n阶)导数。下面是该问题的数学表达:
不仅在节点上与原函数值相同,且还要求与原函数在节点处有相同的一阶(n阶)导数。下面是该问题的数学表达:
对于节点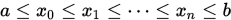 , 寻找插值多项式
, 寻找插值多项式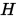 使得
使得
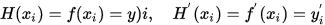
为了求解上述函数,可设两组函数
 分别满足
分别满足(1)
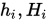 至多都是
至多都是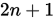 次多项式
次多项式(2) 以下条件成立:

以及
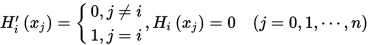
然后可设
 :
: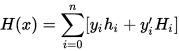
由于
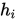 在
在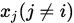 处函数值与导数值均为0,因此必定含有
处函数值与导数值均为0,因此必定含有 , 则令
, 则令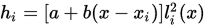 , 其中
, 其中 为拉格朗日基函数,定义为:
为拉格朗日基函数,定义为: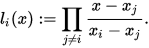
根据
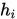 的要求,立即可得到
的要求,立即可得到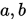 的取值:
的取值: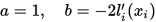
即
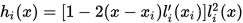
同样的可以得到
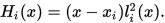
最终得到的埃尔米特插值公式即是
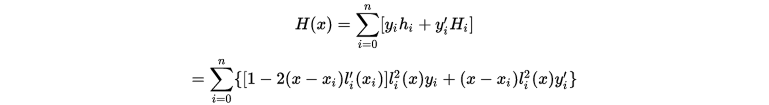
其中
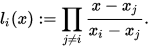
注意到
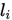 的形式,对于求导运算来说是比较复杂难计算的,因此埃尔米特插值公式常用于较少次数的插值。
的形式,对于求导运算来说是比较复杂难计算的,因此埃尔米特插值公式常用于较少次数的插值。最后,我们给出一个埃尔米特插值的程序,其中对导数的处理则是用的近似值
 :
:
- %Hermite插值法,传入待求x,已知节点xi,yi,yi_diff, 导数参数delta
- function [y] = Hermite(x, xi, yi, yi_diff, delta)
- y = 0; %初始化y
- n = length(xi);
- for i = 1:n
- base_insert = BaseInsert(x, i, n, xi);
- base_insert_diff = (BaseInsert(x+delta, i, n, xi) - BaseInsert(x, i, n, xi)) / delta;
- y = y + (1 - 2 * (x - xi(i)) .* base_insert_diff) .* base_insert .^2 ...
- * yi(i) + (x - xi(i)) .* base_insert .^2 * yi_diff(i);
- end
- end
- function z = BaseInsert(x, i, n, xi)
- z = 1;
- for j = 1:n
- if j ~= i
- z = z .* (x - xi(j)) ./ (xi(i) - xi(j));
- end
- end
- end
测试程序
- %Hermite插值法,传入待求x,已知节点xi,yi,yi_diff, 导数参数delta
- xi = 1:5;
- yi = sin(xi);
- yi_diff = cos(xi);
- delta = 1e-4;
- x = 1:0.1:5;
- y = Hermite(x, xi, yi, yi_diff, delta);
- plot(x,y)
- hold on
- scatter(xi,yi)
给定五个点的插值结果:
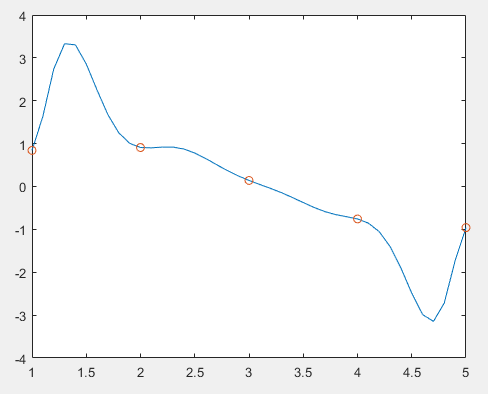
给定10个点的插值结果:
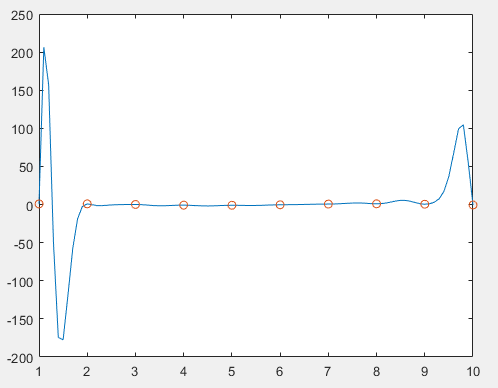
可以看到由于埃尔米特插值的次数为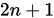 , 因此相比于拉格朗日和牛顿插值法所得到的曲线不太理想。
, 因此相比于拉格朗日和牛顿插值法所得到的曲线不太理想。
二、分段低次插值
为了解决上述提到的高次插值结果不理想问题,考虑每次只插值少数节点,得到分段低次插值法。
由于分段线性插值在节点处不平滑,下面主要考虑分段埃尔米特插值。
设节点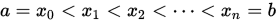 上的函数值为
上的函数值为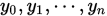 , 分段埃尔米特插值函数
, 分段埃尔米特插值函数 满足
满足
![]() 为区间
为区间![]() 上一阶导数连续的函数。
上一阶导数连续的函数。- 在各节点处函数值和其导数均与原函数相等。
![]() 在每个区间
在每个区间![]() 上面是三次多项式。
上面是三次多项式。
按照埃尔米特插值公式可以直接给出分段的结果:
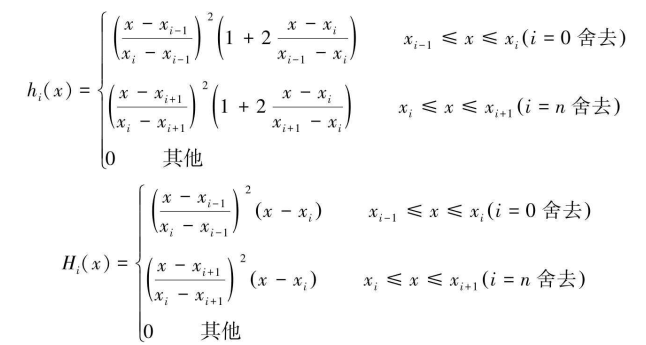
最后插值结果为

上述插值方法在左右两个端点处会强制变为0,此处不知道是否是理解错误
由上式我们给出下述插值程序
- %Hermite插值法,传入待求x,已知节点xi,yi,yi_diff,
- function [y] = SeqHermite(x, xi, yi, yi_diff)
- y = 0; %初始化y
- n = length(x);
- for i = 1:n
- %先找到x对应的位置k
- for k = 1:n
- if x(i) >= xi(k) && x(i) <= xi(k+1)
- break
- end
- end
- y(i) = yi(k) * Calh(x(i), k, xi) + ...
- yi(k+1) * Calh(x(i), k+1, xi) + ...
- yi_diff(k) * CalH(x(i), k, xi) + ...
- yi_diff(k+1) * CalH(x(i), k+1, xi);
- % y(i) = 0;
- % for j = 1:length(xi)
- % y(i) = y(i) + yi(j) * Calh(x(i), j, xi) + yi_diff(j) * CalH(x(i), j, xi);
- % end
- end
- end
- function [hix] = Calh(x, k, xi)
- if k == 1 || k == length(xi)
- hix = 0;
- else
- x1 = xi(k-1);
- x2 = xi(k);
- x3 = xi(k+1);
- if x >= x1 && x <= x2
- hix = ((x-x1)/(x2-x1))^2 * (1 + 2 * (x - x2)/ (x1 - x2));
- elseif x >= x2 && x <= x3
- hix = ((x-x3)/(x2-x3))^2 * (1 + 2 * (x - x2)/ (x3 - x2));
- else
- hix = 0;
- end
- end
-
- end
- function [Hix] = CalH(x, k, xi)
- if k == 1 || k == length(xi)
- Hix = 0;
- else
- x1 = xi(k-1);
- x2 = xi(k);
- x3 = xi(k+1);
- if x >= x1 && x <= x2
- Hix = ((x-x1)/(x2-x1))^2 * (x - x2);
- elseif x >= x2 && x <= x3
- Hix = ((x-x3)/(x2-x3))^2 * (x - x2);
- else
- Hix = 0;
- end
- end
- end
测试程序
- %Hermite插值法,传入待求x,已知节点xi,yi,yi_diff, 导数参数delta
- xi = 1:10;
- yi = sin(xi);
- yi_diff = cos(xi);
- delta = 1e-4;
- x = 1:0.1:10;
- y = Hermite(x, xi, yi, yi_diff, delta);
- plot(x,y)
- hold on
- scatter(xi,yi)
-
- y = SeqHermite(x, xi, yi, yi_diff);
- plot(x,y)
- hold on
- scatter(xi,yi)
最终得到下面的结果
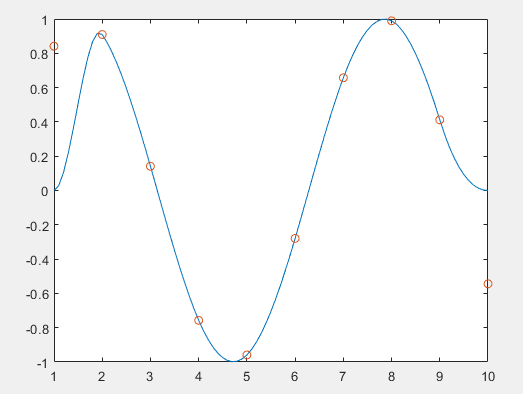
可以明显看到在左右端点处没有和原始值相同,但是在内部的结果则比较理想。
三、Matlab的插值命令
在Matlab中使用interp1()函数进行插值。
使用方法  , 其中
, 其中
- vq是返回的插值
- x是原始节点x坐标
- v是节点对应的函数值
- xq是需要插值的点
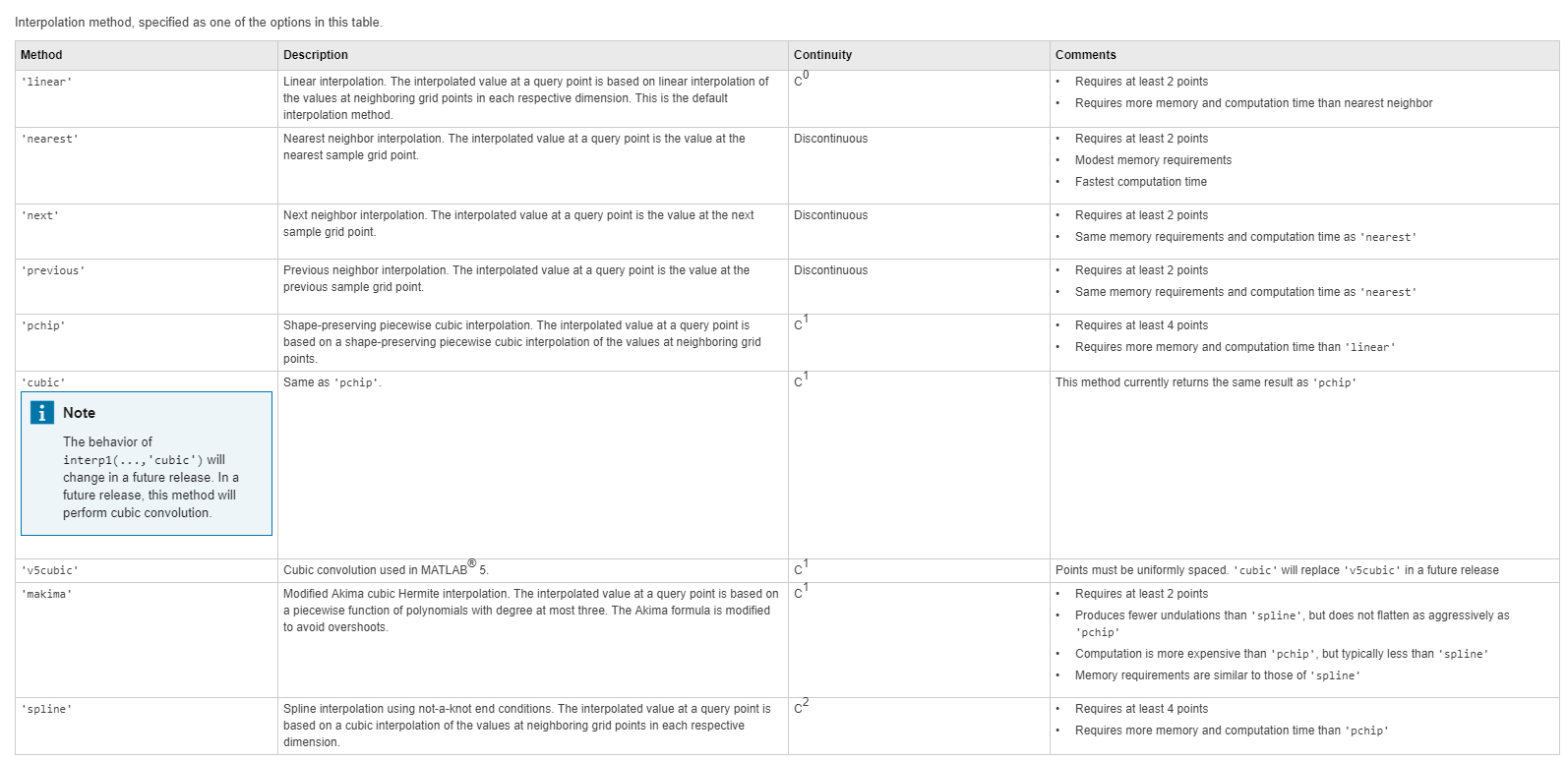
- method。在matlab的文档里面有method的详细介绍:
![method参数解释 method参数解释]()
例子:
- x = 1:10;
- v = cos(x);
- xq = 0:0.1:11;
- methods = ["linear", 'nearest', 'next', 'previous', 'pchip', 'cubic',...
- 'v5cubic', 'makima', 'spline'];
- m = length(methods);
- n = length(xq);
- vq = zeros(n,m);
- for i = 1:m
- vq(:,m) = interp1(x,v,xq,methods(i));
- plot(xq, vq(:,m));
- hold on
- end
- legend(methods)
- hold off
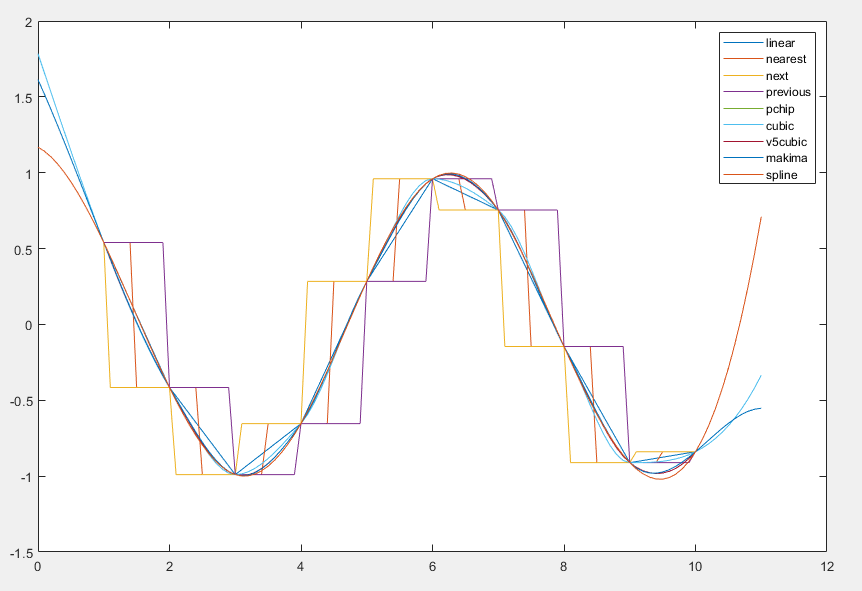
matlab自带函数插值结果
四、两道程序设计习题的解答
- 已知
![]() ,
, ![]() , 用线性插值和三次样条插值求
, 用线性插值和三次样条插值求![]() 的值。
的值。
- x = [0.1, 0.8, 1.3, 1.9,2.5,3.1];
- y = [1.2, 1.6, 2.7, 2.0, 1.3, 0.5];
- xq = interp1(x,y,2)
- xq = interp1(x,y,2,'spline')
- 1990年到2010年每隔10年的产量为75.995, 91.972, 105.711, 123.203, 131.699, 150.697, 179.323, 203.212, 226.505, 249.633, 256.344, 267.893, 给出每隔一年的三次样条插值曲线。
- x = 1900:10:2010;
- y = [75.995, 91.972, 105.711, 123.203, 131.699, 150.697, 179.323, ...
- 203.212, 226.505, 249.633, 256.344, 267.893];
- xq = 1900:2010;
- vq = interp1(x,y,xq,'spline')
- plot(xq,vq)
- hold on
- scatter(x,y)
- hold off
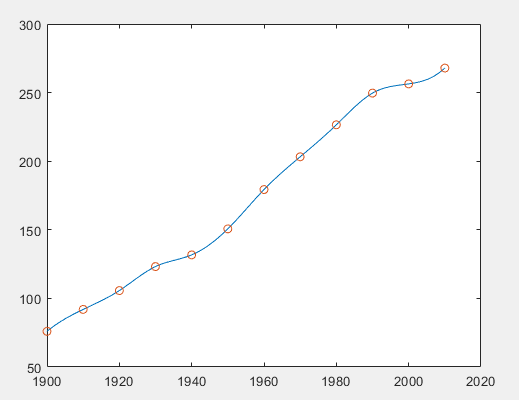
题11

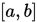
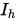


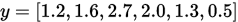
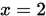

 浙公网安备 33010602011771号
浙公网安备 33010602011771号