Ryoku 的探索题解

2022-09-02 15:14:44 P6037 题解

闲话

当我看见这道绿题的时候，一时没有任何思路（没有看懂作者让我们干什么），看过一些题解的题意分析的我还是不是很清楚（语文太差了），于是，通过对样例的分析，我终于看懂了，题意明白后代码还是好写的（自己模拟才是最靠谱的）。

题意分析

其实不难看出其实题目让我们求的是从每个点开始进行按照美观度 \(p\) 优先和走过的边优先于没走过但是两端点都去过的边的原则来遍历求走过的路程。

如果真的按照这个思路去写， \(10^6\) 的数据显然是不会让你过的，看着样例整齐的数据，我陷入了沉思。

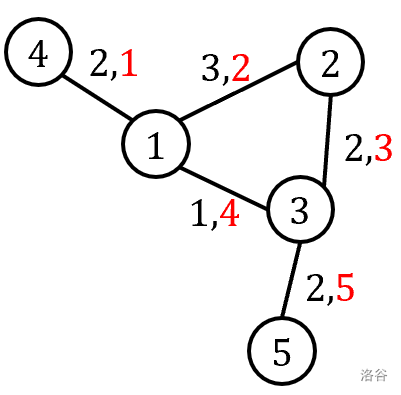(图片来源于原题)

从 \(4\) 出发，先到达处于环内的 \(1\) 中，此时根据 \(p\) 的优先级，我们显然是要选择走到 \(3\) 的，剩下的路就没有选择了，只能除了 \(1\) 到 \(2\) 的路以外全走。

同样，我们从 \(1\) 出发，结果与从 \(4\) 出发相同，从 \(5\) 出发，到 \(3\) 进行选择，\(p_1>p_2\) 于是选择走到 \(1\) 剩下的除了 \(2\) 到 \(3\) 以外的路全走。
从 \(3\) 出发与从 \(5\) 出发结果无异。

那么我们不难得出一个结论：在非环上的点，我们是不需要选择的，也就是非环的路必然要走。

而且，该点进入环中就算是选择，也是在刚进入环时就根据 \(p\) 选择去掉一条边，剩下的边也都要选。

也就是说，所有和环上点连接的非环上点的答案都与环上点相同（都是在该环上点选择去掉一条边），于是解决本题的方法就出来了。

记录所有路的长度之和 \(tot\)，找到环，遍历所有环上点，在与之相连的所有环上点中选择一条 \(p\) 最小的去掉，用 \(tot\) 减去该边的长度即为该环上点的答案，然后再去深搜遍历与该点相连的非环上点，将答案传递。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read(){
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar())if(c=='-')f=-1;
    for(;isdigit(c);c=getchar())x=(x<<1)+(x<<3)+(c^48);
    return x*f;
}
struct Edge{
	int to,w,p,next;
}edge[2000006];  //我用的链式前向星 
int n,pd[1000006],ent,head[1000006]; //因为我用的是拓扑，这个pd表示每个点的度 
ll tot,ans[1000006];//总长度和每个点的答案 ，最好开long long 
bool vis[1000006];//最后遍历树的时候防止重复赋值 
queue<int>Q;//拓扑的队列 
inline void add(int u,int v,int w,int p){
	edge[++ent].to=v;
	edge[ent].w=w;
	edge[ent].p=p;
	edge[ent].next=head[u];
	head[u]=ent;
	return;
}
inline void dfs(int x){
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(pd[y]<2&&!vis[y]){//度为一就是只有一条边连接，是非环节点 
			ans[y]=ans[x];//赋值 
			vis[y]=1;
			dfs(y);
		}
	}
}
int main(void){
    n=read();
    for(int i=1;i<=n;i++){
    	int u=read(),v=read(),w=read(),p=read();
    	add(u,v,w,p),add(v,u,w,p);
    	pd[u]++,pd[v]++;//度数加 
    	tot+=w;//累加答案 
	}
	for(int i=1;i<=n;i++){
		if(pd[i]==1)Q.push(i);//叶子节点就push 
	}
	while(!Q.empty()){//没什么好说的 
		int x=Q.front();
		Q.pop();
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to;
			if(--pd[y]==1){
				Q.push(y);
			}
		}
	}
	for(int x=1;x<=n;x++){
		if(pd[x]>=2){// 度超过一说明在环上 
			int minn=0x3f3f3f3f,jian;
			for(int i=head[x];i;i=edge[i].next){
				int y=edge[i].to;
				if(pd[y]>=2&&edge[i].p<minn){//去找同样是环上的最小p的边删除 
					minn=edge[i].p;
					jian=edge[i].w;
				}
			}
			ans[x]=tot-jian;//得到删除这条边后的答案 
			dfs(x);
		}
	}
	for(int i=1;i<=n;i++){
		printf("%lld\n",ans[i]);
	}
	return 0;
}

如果还没看懂建议自己模拟一下就知道了。