排序算法（js版本）

几个概念
1、稳定排序：如果 a 原本在 b 的前面，且 a == b，排序之后 a 仍然在 b 的前面，则为稳定排序。
2、非稳定排序：如果 a 原本在 b 的前面，且 a == b，排序之后 a 可能不在 b 的前面，则为非稳定排序。
3、原地排序：原地排序就是指在排序过程中不申请多余的存储空间，只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
4、非原地排序：需要利用额外的数组来辅助排序。

1.冒泡

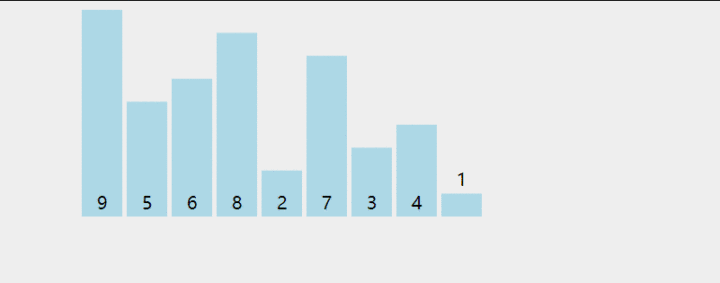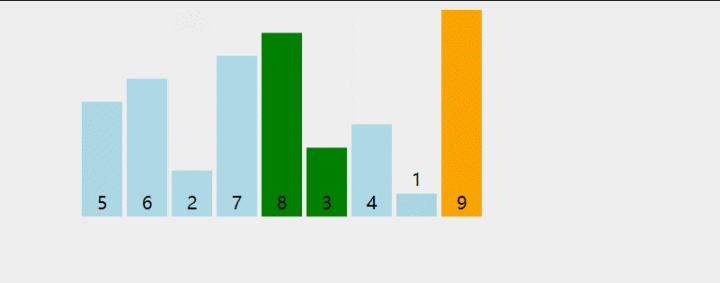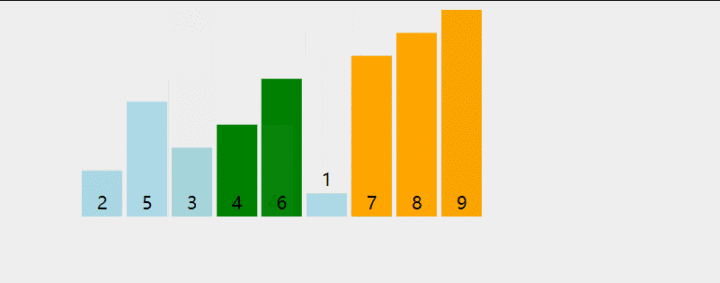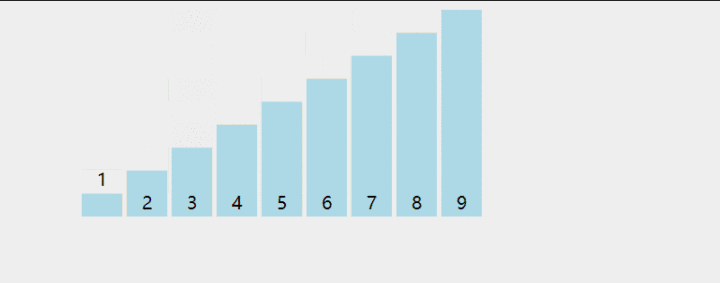
思想：把第一个元素与第二个元素比较，如果第一个比第二个大，则交换他们的位置。接着继续比较第二个与第三个元素，如果第二个比第三个大，则交换他们的位置....

未优化

int [] arry={2,4,1,0,8,5};
      int n=arry.length;
      int temp;
      for (int i = 0; i <n ; i++) { //  从0-i有序
            for (int j = 0; j <n-i-1 ; j++) {
                if (arry[j]<arry[j+1]){
                    temp=arry[j];
                    arry[j]=arry[j+1];
                    arry[j+1]=temp;
                }
            }
        }

优化
相邻的元素之间都没有发生交换的操作，这意味着右边的元素总是大于等于左边的元素，此时的数组已经是有序的了.

for (let i = 0; i < a.length; i++) {
    let flag = false;
    let temp;
    for (let j = 0; j < a.length - i - 1; j++) {
        if (a[j] > a[j + 1]) {
            flag = true;
            temp = a[j];
            a[j] = a[j + 1];
            a[j + 1] = temp
        } 
    }
     //如果没有交换，直接退出循环
     if (!flag) {
        break;
    }
}

插入排序

思路：
1、从数组第2个元素开始抽取元素。

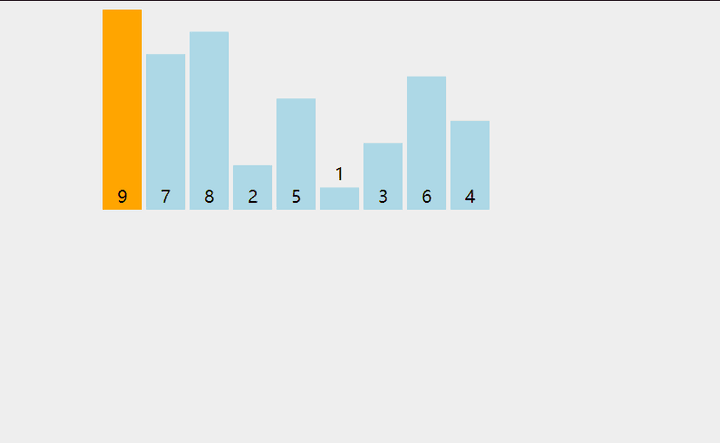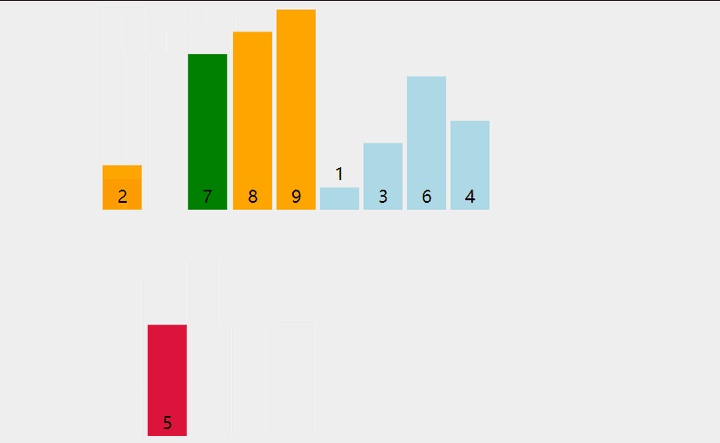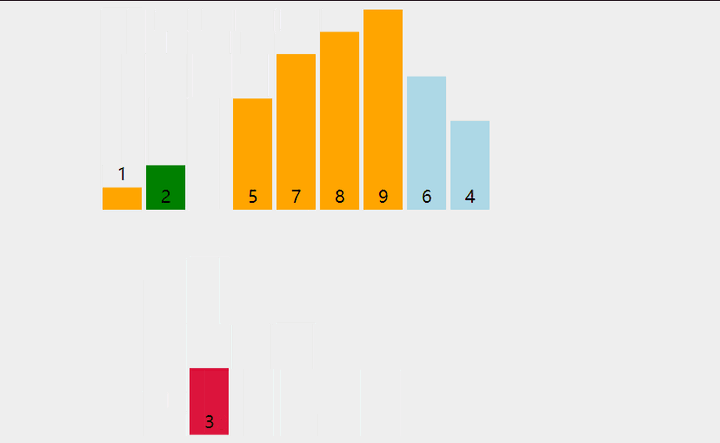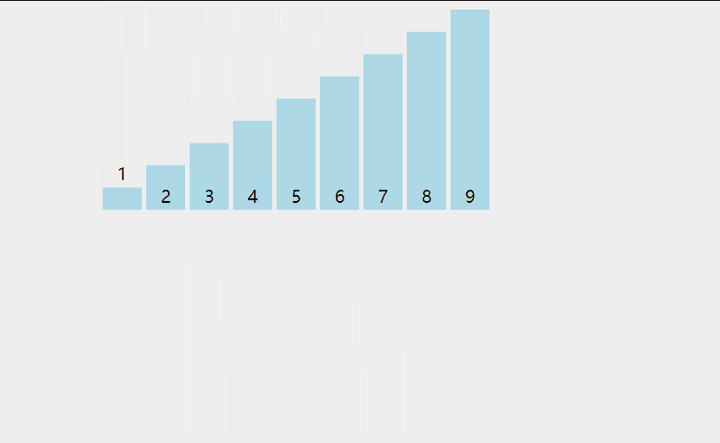
2、把它与左边第一个元素比较，如果左边第一个元素比它大，则继续与左边第二个元素比较下去，直到遇到不比它大的元素，然后插到这个元素的右边。

3、继续选取第3，4，....n个元素,重复步骤 2 ，选择适当的位置插入。
交换结束的条件:
1.左边没有数可以比较了。
2.不比左边的数小了。
（想象下打斗地主的情景）

let a = [1,4,5,1,2,9,0,3];
for(let i=1;i<a.length;i++){
    for(let j=i-1;j>=0 && a[j]>a[j+1]; j--){
    //这里用了解构来交换值
      [a[j],a[j+1]]=[a[j+1],a[j]];
    }
}

性质：
1、时间复杂度：O(N*N)

• 最坏：4 5 6 7 3 2 1 O(N*N)

• 最好：1 2 3 4 5 6 7 O(N)不需要交换

2、空间复杂度：O(1) 3、稳定排序 4、原地排序
注意这里不能自己写个swap（）函数来交换，牵扯到作用域的问题。
交换两个值有很多方法！

3.选择排序

思路：
1.在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置
2.再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。
3.以此类推，直到所有元素均排序完毕。

let a = [1,4,5,1,2,9,0,3];
let min;//无序区的最小值
let i;//有序区的末尾位置
let j;//无序区的开始位置
for( i=0;i<a.length;i++){
     min=i;
     //找出a[i+1]-a[n]之间最小的元素
     for(j=i+1;j<a.length;j++){
        if(a[j]<a[min]){
            //更新无序区最小值的位置
            min=j;
        }
     }
     //若min!=i，则交换 a[i] 和 a[min]。
     //交换后，保证了a[0]..a[i]之间元素有序
     if(min!=i){
        [a[min],a[i]]=[a[i],a[min]];
     }
    
}

性质：1、时间复杂度：O(n2) 2、空间复杂度：O(1) 4、原地排序
稳定性得具体问题具体分析
不同的实现方法有不同的结果.

• 如果是在数组中交换,那么就有可能不稳定,如
• 如果是链表或者开一个新的数组（自然不会破坏相同元素的相对位置）,那么又是稳定的。
  则可以这样说，当空间复杂度为O(1)的时候，是不稳定的。

---

《算法》p217,有提到，有很多办法可以将任意排序算法变成稳定的，但是，往往需要额外的时间或者空间。

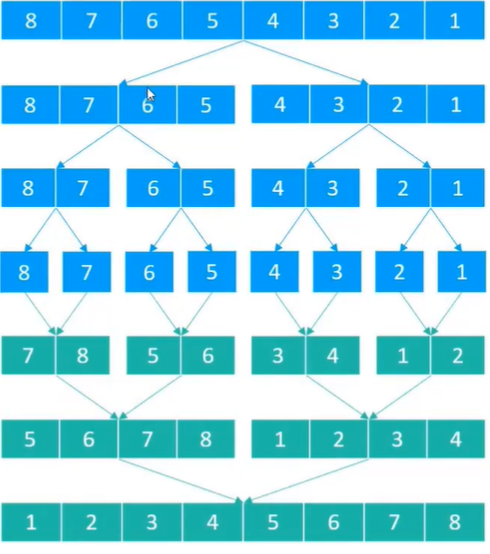
4.归并排序

思路：

• 1)整体就是一个简单递归，左边排好序、右边排好序、让其整体有序
• 2)让其整体有序的过程里用了排外序方法
• 3)利用master公式来求解时间复杂度
• 4)归并排序的实质

function merge(arry,left,mid,right){
    let size=right-left+1;
    let help=new Array(size);
    let p1=left;
    let p2=mid+1;
    let i=0;
    while(p1<=mid && p2<=right){
        help[i++]=arry[p1]<arry[p2]?arry[p1++]:arry[p2++];
    }
    while(p1<=mid){
        help[i++]=arry[p1++];
    }
    while(p2<=right){
        help[i++]=arry[p2++];
    }
    for(let j=0;j<help.length;j++){
        arry[left+j]=help[j];
    }
}

function sort(arry,left,right){
    if(left === right){
        return;
    }else {
        let mid = left + Math.floor((right - left) / 2);
        sort(arry, left, mid);
        sort(arry, mid + 1, right);
        merge(arry, left, mid, right);
    }
}
let a = [1,4,5,1,2,9,0,3];

sort(a,0,a.length-1);
console.log(a);

let mid = left + Math.floor((right - left) / 2);
这里一定注意下！

快速排序

思想：随机选取一个数，人为的把它放在最后，用它最后做划分。
最坏情况下时间复杂度是O(n²)
随机选取比较的那个值，数组中每个值被选到的概率都是1/n，最后时间复杂度求数学期望后是O(nlogn)。
空间复杂度也是概率累加求数学期望，是O(logn)

 public static void main(String []args){
            int [] arry={3,5,1,1,4,5};
            int n=arry.length;
            quickSort(arry);
            for (int i = 0; i <n ; i++) {
                System.out.println(arry[i]);
            }

        }

        public static void quickSort(int[] arr) {
            if (arr == null || arr.length < 2) {
                return;
            }
            quickSort(arr, 0, arr.length - 1);
        }

        public static void quickSort(int[] arr, int l, int r) {
            //这个是递归的出口
            if (l < r) {
                swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
                //p是划分值等于区域的范围，左右边界,只有两个值
                int[] p = partition(arr, l, r);
                //p[0] - 1 小于区域的右边界
                quickSort(arr, l, p[0] - 1);
                //p[1] + 1 大于区域的左边界
                quickSort(arr, p[1] + 1, r);
            }
        }

        //左侧<划分值、中间==划分值、右侧>划分值
        //2)对左侧范围和右侧范围，递归执行
        public static int[] partition(int[] arr, int l, int r) {
            int less = l - 1;//左边边界
            int more = r;//右区边界
            while (l < more) {
                if (arr[l] < arr[r]) {
                    //++less，先自增，再赋值，因为是和<区的下一个数交换
                    //l++,先赋值，再自增,
                    swap(arr, ++less, l++);
                } else if (arr[l] > arr[r]) {
                    // --more，先自减，再赋值，因为是和>区的前一个数交换
                    // l原地不变，因为是新过来的，原地不能变，还得比较
                    swap(arr, --more, l);
                } else {
                    //arry[L]=arry[r]，往下移动，l其实是个游标
                    l++;
                }
            }
            //more是第一个等于num的下标
            swap(arr, more, r);
            //more的值赋给r
            //less是<区的边界，less+1就成了等于区
            return new int[] { less + 1, more };
        }

        public static void swap(int[] arr, int i, int j) {
            int tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
        }

left是移动的指针
步骤：

• 1）arr[left]< arr[right] 也就是被随机选出来的那个数，则当前数与小于区域的下一个数做交换，小于区域右扩，left++（指针移动）。
• 2）arr[left]> arr[right],则当前数与大于区域的前一个数做交换，大于区域右扩，但是！left指针不移动因为这次交换过来的数没有进行判断（它是属于哪个区域的）
• 3）arr[left]= =arr[right]，此时就应该放到等于区域，不移动，left++；

循环的结束条件是： left= =more，指针走到了大于区域。

js版

swap写的不太优雅？

function sort(a,left,rigth){
   if(left<rigth){
      let swap=left+Math.floor(Math.random()*(rigth-left+1));
      let temp=a[swap];
      a[swap]=a[rigth];
      a[rigth]=temp;
      let p=patition(a,left,rigth);
      sort(a,left,p[0]);
      sort(a,p[1]+1,rigth)
   }
}
function patition(a,left,rigth){
   let more=rigth;
   let less=left-1;
   while(left<more){
      if(a[left]<a[rigth]){
         let temp=a[left];
         a[left++]=a[++less];
         a[less]=temp;
      }else if(a[left]>a[rigth]){
         let temp=a[left];
         a[left]=a[--more];
         a[more]=temp;
      }else{
         left++;
      }
   }
   let temp=a[more];
   a[more]=a[rigth];
   a[rigth]=temp;
   //这里 more和rigth,交换了，所以上面p[1]+1
   return [less,more];
}
let a=[1,4,2,0,8,2,7];
sort(a,0,a.length-1);
console.log(a);

具体过程

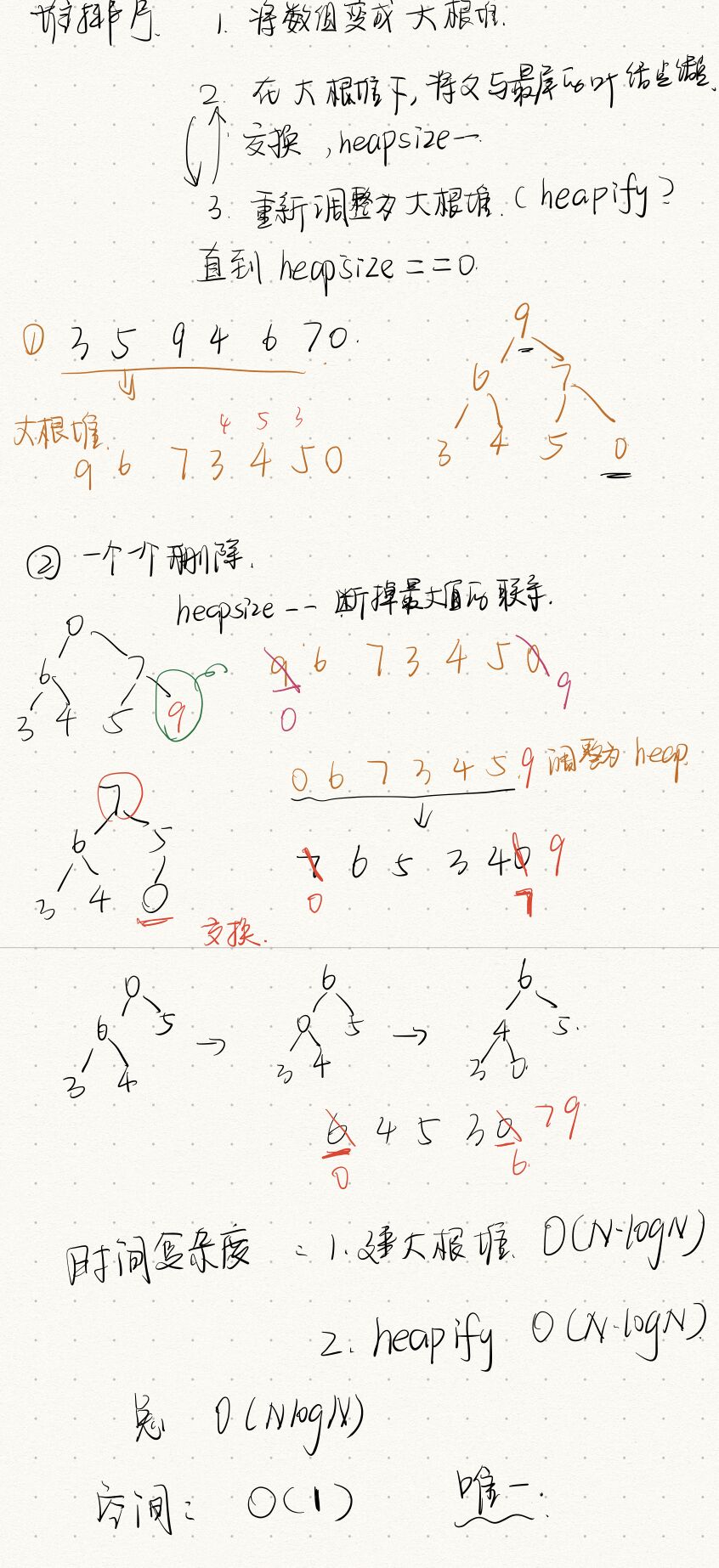
6.堆排序

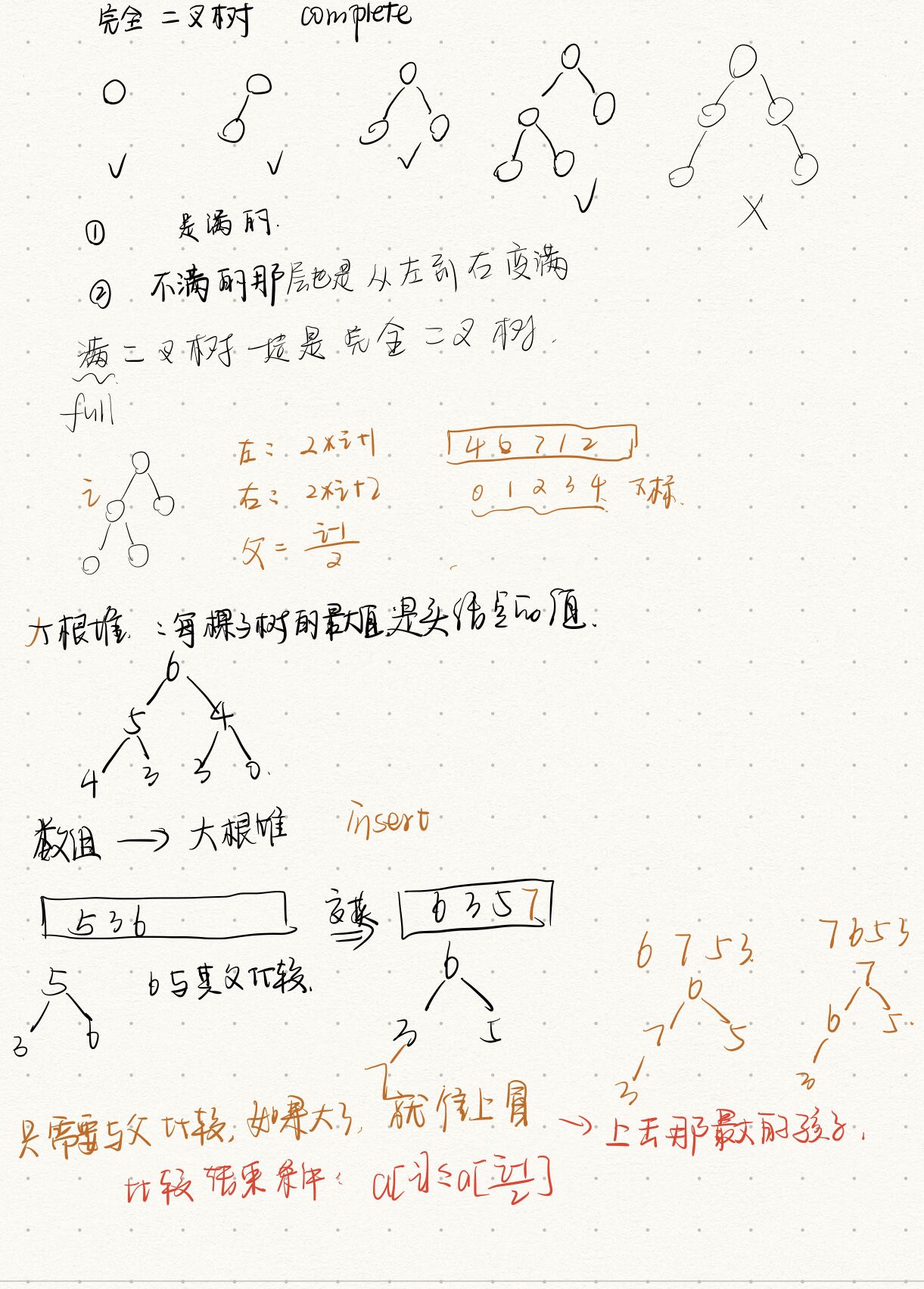
补充 ：堆结构（重要）

• 堆结构就是用数组实现的完全二叉树结构
• 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
• 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
• 堆结构的heap Insert与heapify操作
• 堆结构的增大和减少
• 优先级队列结构，就是堆结构
  
  
  

java

public class HeapSort {
    public static void main(String []args) {
        int[] arry = {6, 4, 1, 0, 8, 5};
        int n=arry.length;
        heapSort(arry);
        for (int i = 0; i <n ; i++) {
            System.out.println(arry[i]);
        }
    }
    public static void heapSort ( int[] arr){
            if (arr == null || arr.length < 2) {
                return;
            }
            for (int i =0; i < arr.length; i++) {
                heapInsert(arr, i);
            }
            int size = arr.length;
            //这里交换0和最末尾的数
            swap(arr, 0, --size);
            //循环结束条件是堆的大小为0
            while (size > 0) {
                heapify(arr, 0, size);
                swap(arr, 0, --size);
            }
        }

        public static void heapInsert ( int[] arr, int index){
        //插入的元素如果比他的父元素要大，应该换，这个步骤后，形成了堆结构
            while (arr[index] > arr[(index - 1) / 2]) {
                swap(arr, index, (index - 1) / 2);
                index = (index - 1) / 2;
            }
        }

        public static void heapify ( int[] arr, int index, int size){
            //left是左边孩子
            int left = index * 2 + 1;
            //如果没有左孩子肯定也没有右孩子，所以是左孩子为条件
            while (left < size) {
                //判断两个孩子哪个孩子的数值大,右>左 得满足两个条件：1.没有越界 2.右>左。否则的话是左大
                int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
                // 父亲和较大的孩子之间，谁的值大，把下标给largest
                largest = arr[largest] > arr[index] ? largest : index;
                //父亲连同孩子的范围内是最大的，不需要往下走了
                if (largest == index) {
                    break;
                }
                swap(arr, largest, index);
                //index往下走
                index = largest;
                left = index * 2 + 1;
            }
        }

        public static void swap ( int[] arr, int i, int j){
            int tmp = arr[i];
            arr[i] = arr[j];
            arr[j] = tmp;
        }
}

JS

let a=[3,2,7,1,7,0];
function heapSort(a) {
    if (a.length<2){
        return;
    }
    for (let i=a.length-1;i>=0;i--){
        heapify(a,i,a.length);
    }
    let heapSize=a.length;
    heapSize--;
    [a[0],a[heapSize]]=[a[heapSize],a[0]];

    while(heapSize>0){
        heapify(a,0,heapSize);
        //交换
        heapSize--;
        [a[0],a[heapSize]]=[a[heapSize],a[0]];
    }
}
function  heapify(a,index,size) {
    let left=index*2+1;
    //size不是索引
    while(left<size){
        let largest=left+1<size&& a[left+1]>a[left]? left+1:left;
        largest=a[index]>a[largest]?index:largest;
        if (largest===index){
            break;
        }
        //交换
        [a[largest],a[index]]=[a[index],a[largest]];
        //更新left index的值
        index=largest;
        left=index*2+1;
    }
}
heapSort(a);
console.log(a)

这里注意下！size值的范围是不是索引的范围！！是堆的个数。范围比数组下标多1