链表相关题目
92 反转链表M
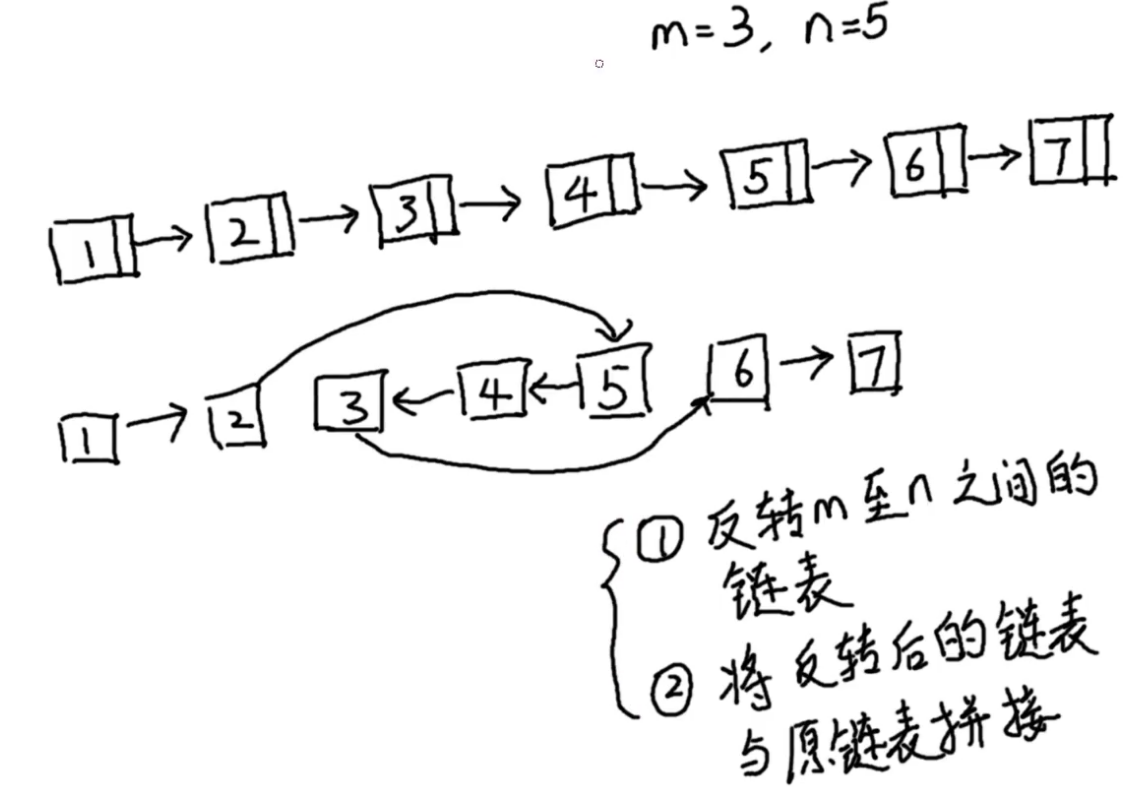
思想:
1.反转[left,right]之间的链表
2.将反转后的链表连接起来
这题其实不难,做的时候可以画图草图理解,注意边界条件
步骤:
1.先用for循环遍历,找到需要反转的的第一个结点。注意i是从1开始(索引从1开始),同时定义两个临时变量pre2 cur2,保存当前的位置。cur是当前位置,pre是当前结点的前一共个结点。
2.找到位置后,开始反转链表。这里还是要注意for的循环条件,m<=right,一共for循环要遍历 right-left+1次。其实意思就是需要遍历完需要反转的链表。循环结束后,cur指向索引为right的下一个结点(如果为空,也不影响),pre指向索引为right的结点。
3.连接三部分链表。
- 前半段连接反转后链表的头部,这时需要判断left是否为1,如果为1,也就是从头部反转的,需要给head复制(最终函数返回的是head),head=pre;非1,pre.next=pre2
- 反转链表尾部连接后半段,cur2.next=cur。如果没有后半段cur为null,也不影响。


class Solution {
public ListNode reverseBetween(ListNode head, int left, int right) {
if(head.next==null){
return head;
}
ListNode pre=head;
ListNode cur=head;
ListNode pre2=pre;
ListNode cur2=cur;
for(int i=1;i<left;i++){
pre=cur;
cur=cur.next;
}
pre2=pre;
cur2=cur;
for(int m=left;m<=right;m++){
next=cur.next;
cur.next=pre;
pre=cur;
cur=next;
}
while
if(left>1){//pre2!=null,如果是从头开始反转的,注意头结点
pre2.next=pre;
}else{
head=pre;
}
cur2.next=cur;
return head;
}
}
25. K 个一组翻转链表H
这个题算法不难,但是需要细心!注意边界条件.
一(需要获取到链表长度,遍历两次)
时间复杂度高但是空间复杂度低些.
把链表分成了三块
核心是 上一次翻转后的尾部要连接下一次(当前)翻转子链表的头部.所以需要有两个变量来保存这两个指针.
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
//k==1时,输出原链表
if(k==1){
return head;
}
int count=0;
ListNode current=head;
while(current!=null){
count++;
current=current.next;
}
int turns=count/k;
current=head;
// after befor 是记录循环中上一次的翻转的那一块链表的头和尾
ListNode before=null;
ListNode after=null;
ListNode result=null;
for(int i=0;i<turns;i++){
//这是当前翻转后链表的头和尾 [1,2,3,4] 注意是1是tail,4是head!!
ListNode thisHead=null;
ListNode thisTail=null;
ListNode pre=null;
for(int j=0;j<k;j++){
if(j==0){
thisTail=current;
}else if(j==k-1){
thisHead=current;
}
//最基础的翻转链表
ListNode next=current.next;
current.next=pre;
pre=current;
current=next;
}
//开始连接翻转后的链表,上一次的翻转后的链表组的尾部连接新翻转链表组的头部
if(after==null && before==null){
//这里是第一次
result=thisHead;
}else{
after.next=thisHead;
}
//更新after
before=thisHead;
after=thisTail;
}
//如果还有剩下不足的k个的,连接
after.next=current;
return result;
}
}
只需要遍历一次
时间复杂度低但是空间复杂度高些

class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode dummy=new ListNode(0);
dummy.next=head;
ListNode pre=dummy;
ListNode end=dummy;
ListNode next=null;
ListNode start=null;
while(end!=null){
for(int i=0;i<k && end!=null;i++){
end=end.next;
}
if(end==null){
break;
}
next=end.next;
start=pre.next;
end.next=null;
//start本来是头部的,但是翻转后,start指向尾部了
pre.next=reverse(start);
start.next=next;
pre=start;
end=pre;
}
return dummy.next;
}
public ListNode reverse(ListNode head){
ListNode temp=null;
ListNode next=null;
ListNode cur=head;
while(cur!=null){
next=cur.next;
cur.next=temp;
temp=cur;
cur=next;
}
return temp;
}
}
这里注意虽然子链表翻转后,链表的头部和尾部调换了,start不需要显式的更改,因为 reverse()返回的是翻转后子链表的头部,而start指针指向的链表根本没有变!!,直接指向子链表的尾部!
eg: 1->2->3->4, 翻转前 start指向1
翻转后 链表变成了4->3->2->1;start 还是指向了1,此时start是子链表的尾部.
这里注意和法一区别下.
看下面这个图

141. 环形链表E
https://leetcode-cn.com/problems/linked-list-cycle/
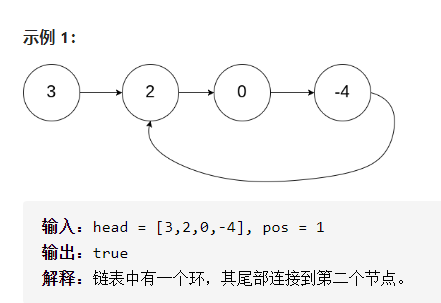
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
public class Solution {
public boolean hasCycle(ListNode head) {
//只有一个结点或者结点为空,直接返回false
if(head==null||head.next==null){
return false;
}
ListNode slow=head;
ListNode fast=head.next;
while(slow!=fast){
//首先判断用 fast来判断情况,fast跑的快,不能用slow来判断,因为可能存在fast.next==null
if(fast.next==null|| fast.next.next==null){
return false;
}
slow=slow.next;
fast=fast.next.next;
}
return true;
}
}
其实用到是Floyd 判圈算法,使用快慢指针(双指针)证明有点麻烦先不了解。定义两个指针,一快一满。慢指针每次只移动一步,而快指针每次移动两步。初始时,慢指针在位置 head,而快指针在位置head.next。这样一来,如果在移动的过程中,快指针反过来追上慢指针,就说明该链表为环形链表。否则快指针将到达链表尾部,该链表不为环形链表。
注意:规定初始时慢指针在位置 head,快指针在位置 head.next,而不是两个指针都在head位置。主要是使用的是while循环,循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合,如果我们将两个指针初始都置于 head,那么 while 循环就不会执行。因此,我们可以假想一个在 head 之前的虚拟节点,慢指针从虚拟节点移动一步到达 head,快指针从虚拟节点移动两步到达 head.next,这样我们就可以使用 while 循环了。
当然,我们也可以使用 do-while 循环。此时,我们就可以把快慢指针的初始值都置为 head。(摘抄于力扣题解)[题解](https://leetcode-cn.com/problems/linked-list-cycle/solution/huan-xing-lian-biao-by-leetcode-solution/)
142.环形链表2 (M)
算法的正确性:Floyd 判圈算法
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head ==null || head.next == null){
return null;
}
ListNode fast=head;
ListNode slow=head;
while(true){
if(fast==null || fast.next==null){
return null;
}
fast=fast.next.next;
slow=slow.next;
if(slow==fast){
break;
}
}
//其实只是需要将其中的一个指针指向链表头部就行
slow=head;
while(slow!=fast){
slow=slow.next;
fast=fast.next;
}
return fast;
}
}
算法:
1.定义两个快慢指针,快指针比慢指针多走一步。
2.如果两个指针没有相遇,则说明没有环,返回null;
3.如果相遇,将其中一个指针指向链表头部,此时两个指针每次都只走一步,则相遇时,时环的入口结点。
21.合并两个有序链表 easy(与剑指offer同题)
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head=new ListNode(0);
ListNode temp=head;
//注意这里需要有一个头指针head来保存,如果不保存,最后temp只能获得到合并链表的最后一个元素
while(l1!=null&&l2!=null){
if(l1.val<l2.val){
temp.next=l1;
temp=temp.next;
l1=l1.next;
}else{
temp.next=l2;
l2=l2.next;
temp=temp.next;
}
}
if(l1!=null){
temp.next=l1;
}
if(l2!=null){
temp.next=l2;
}
//注意返回的是什么
return head.next;
}
}
160. 相交链表(easy)
1.HashSet法(空间复杂度高O(N))
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode a=headA;
ListNode b=headB;
HashSet<ListNode> node=new HashSet<>();
while(a!=null){
node.add(a);
a=a.next;
}
while(b!=null){
if(node.contains(b)){
return b;
}
b=b.next;
}
return null;
}
}
2.双指针
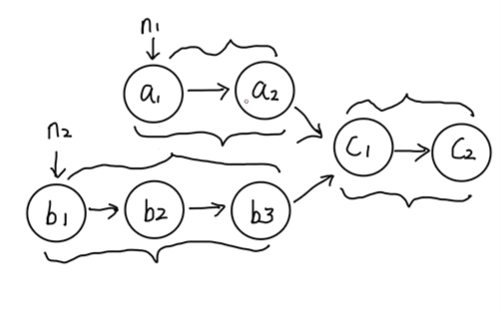
使用双指针,空间复杂度将为O(1)
短链表a,长链表b,短链表先走到底,此时将短链表指向较长的链表,一段时间后长链表也走到底,长链表指向短。最后肯定会在相交处相遇。
这个做法消除了两个链表的长度差!!a+b=b+a;
var getIntersectionNode = function(headA, headB) {
let a = headA;
let b = headB;
while(a!=b){
if(a!== null){
a = a.next;
}else{
a = headB;
}
if(b !==null){
b = b.next;
}else{
b = headA
}
}
return a;
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号