DataWhale八月组队学习-李宏毅深度学习Task05-网络设计的技巧
类神经网络的训练
局部最小值与鞍点
-
背景:随着参数更新,
training loss没有下降到足够小或者压根没有下降趋势。人们推测是走到的这些地方参数对loss的微分为零时,梯度下降无法再updata参数。 -
gradient为零的两种情况(统称为临界点)-
局部最小值:
local minima,卡在此处,无路可走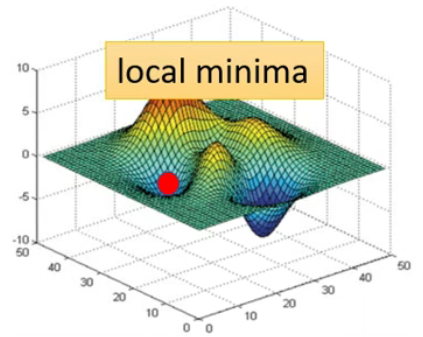
-
鞍点:
saddle point,卡在此处,有路可循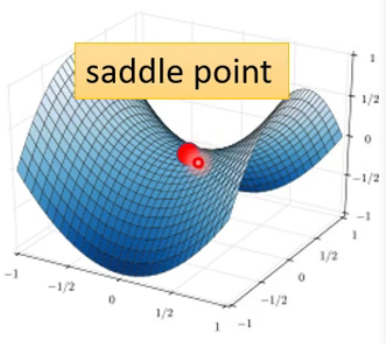
-
-
如何分析得出是卡在局部最小值还是卡在鞍点
-
泰勒多项式
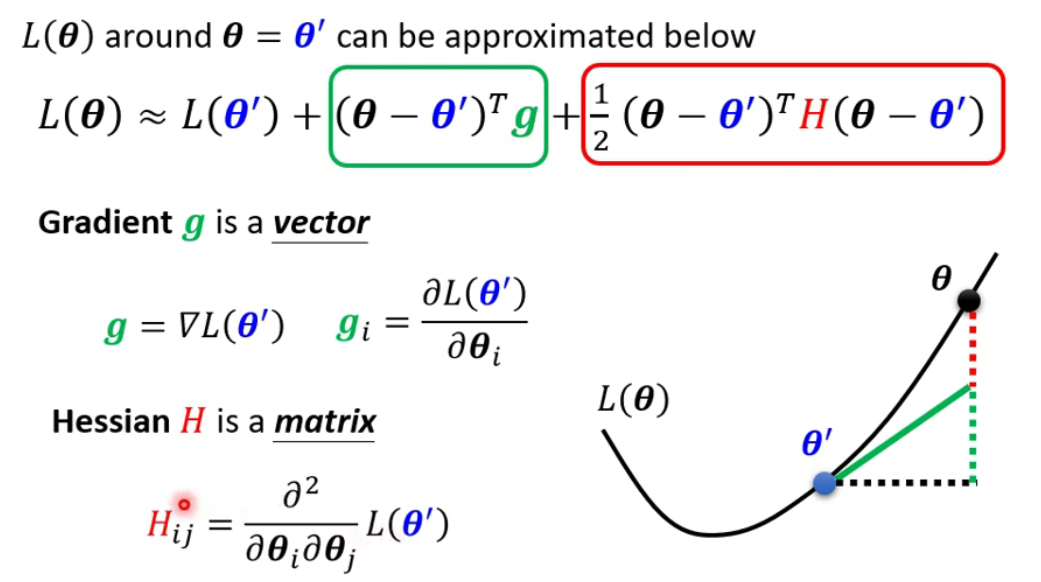
简单理解就是损失函数的泰勒展开式和梯度(具有一次微分的项目)、海塞矩阵(具有二次微分的项目)有关。
-
当
gradient为0时,我们可以根据点的分布来判断当前点的位置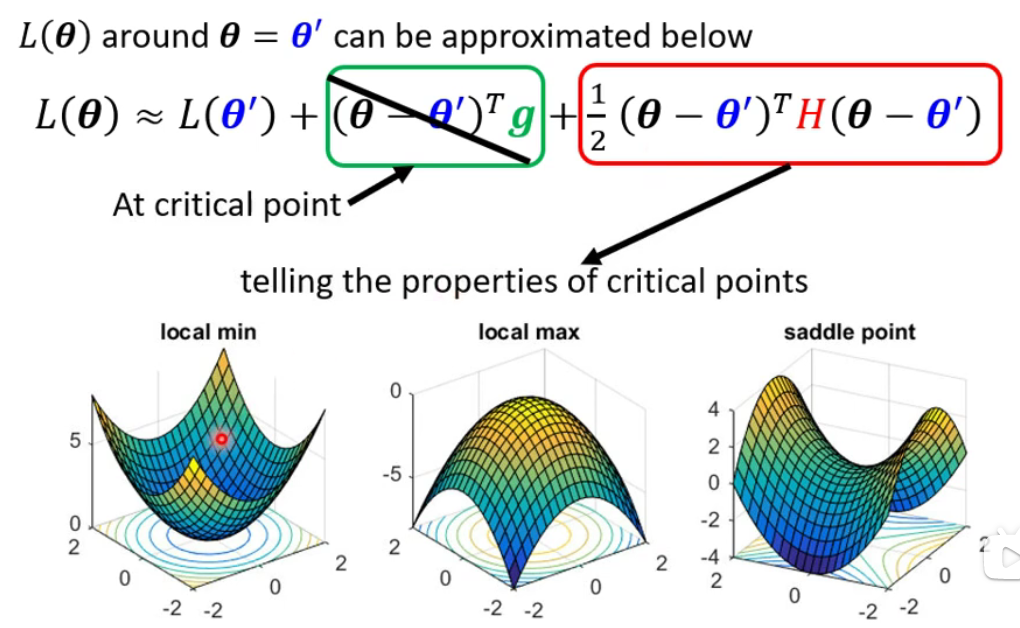
-
可能情况
算出一个
Hession,不需要将其和所有的v相乘。只需要看这个Hession的所有特征值都是整的,就代表这个条件成立。
-
-
卡在
saddle point-
Hession不仅可以判断当前卡住的位置是不是在saddle point,还可以指出了参数可以更新的方向。 -
当
gradient已经无法判断参数更新方向的时候
-
批次(Batch)与动量(Momentum)
-
利用
batch进行优化- 当我们进行参数更新的时候,我们是将所有的
data分为一个个的batch。每次更新参数就会使用一笔batch。所有的batch都进行一遍叫做一个epoch - 将资料分为
batch的过程叫做Shuffle,每次epoch开始之前会切分一次batch,所以每一个epoch对应的batch都不一样。
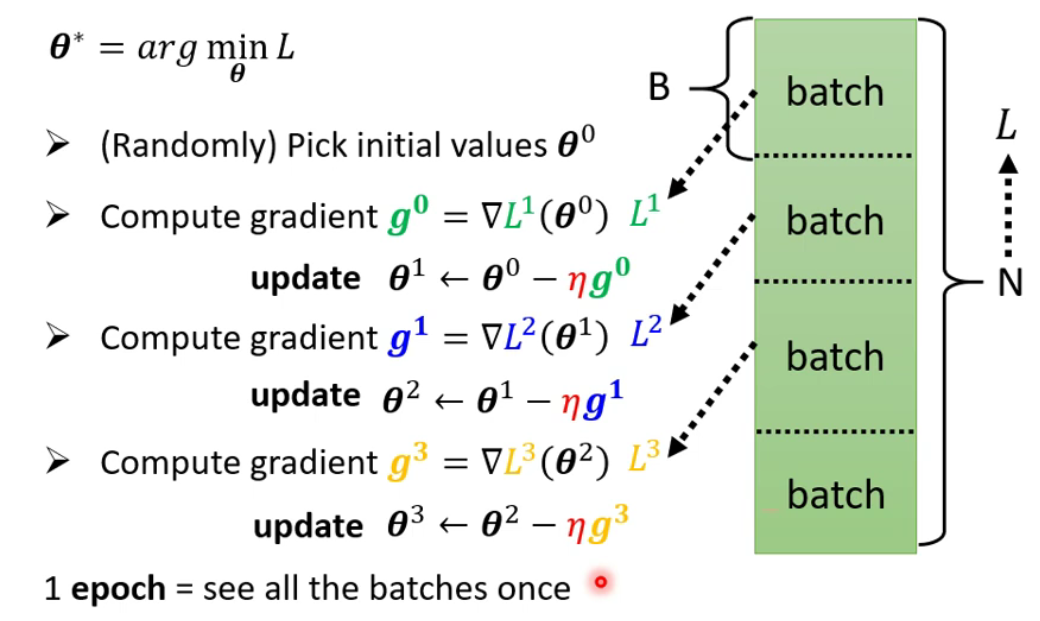
- 当我们进行参数更新的时候,我们是将所有的
-
为什么要使用
batch-
进行
batch和不进行batch情况的比较- 左边不进行
batch的情况冷却时间较长,但一步走的较为稳健(Powerful)。右边进行batch的情况冷却时间较短,但每一步走的不稳定(Noisy)。 - 由于
GPU可以进行并行运算的关系,所以batch size可能对花费时间的影响非常小。
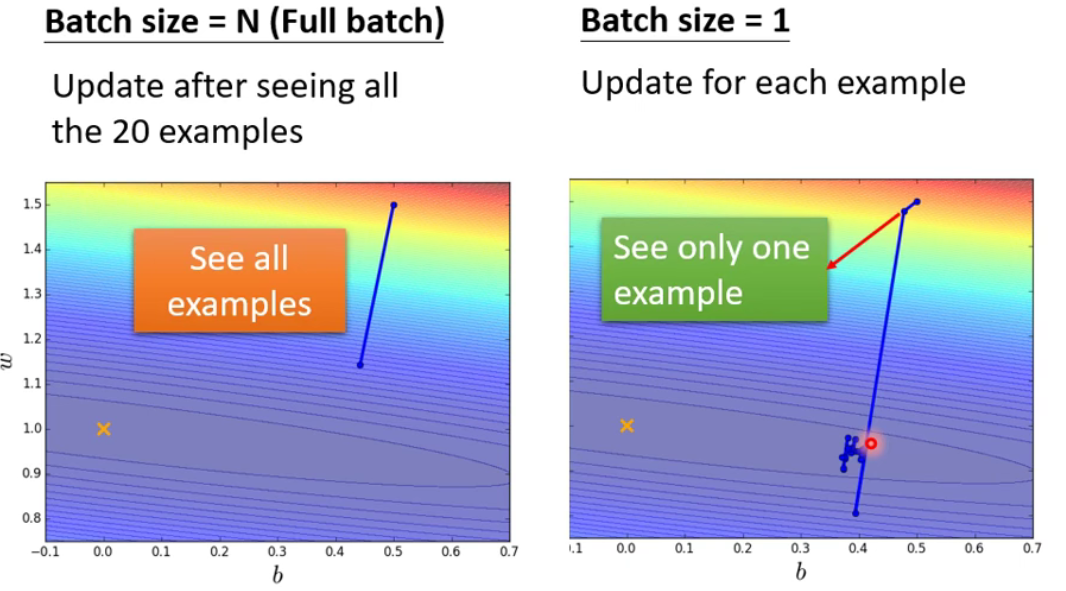
- 左边不进行
-
size大小对Batch的影响size的大小越大,需要参数更新的次数就越小,可能batch size大的batch进行一个epoch的时间更短。- 综上所述,使用GPU进行并行运算时不进行
batch不一定冷却时间比进行batch花费时间长

-
小
Batch与大Batch的比较Noisy的梯度下降反而可以帮助training
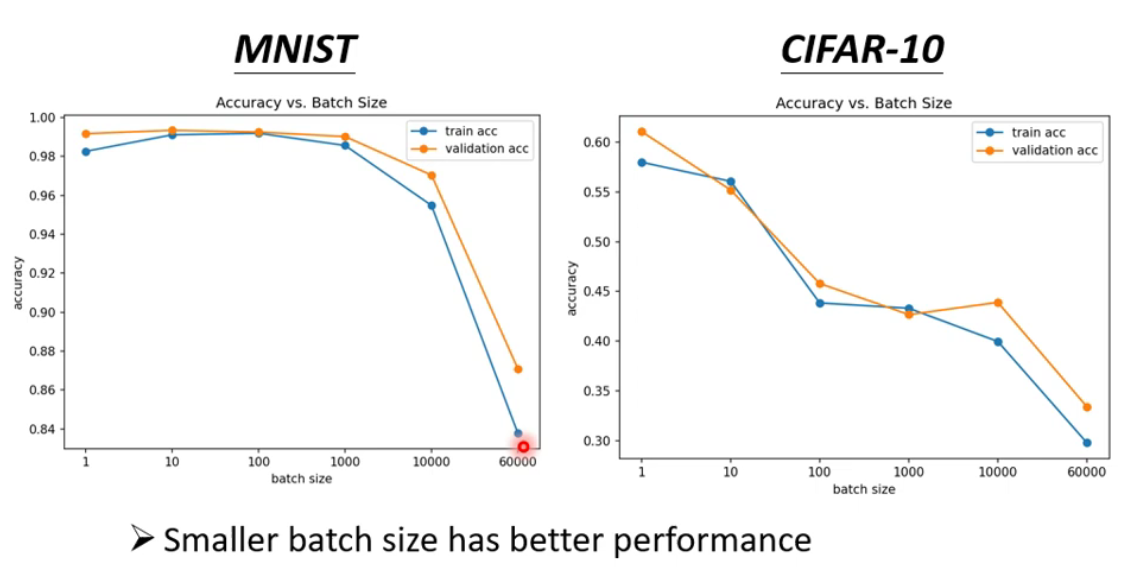
- 原因:如果是
full Batch,在遇到local minimum或者saddle point的时候参数更新就会停止。而如果是Small Batch,每一次使用的损失函数会有略微区别,使得遇到上述情况的时候可以继续进行下去。
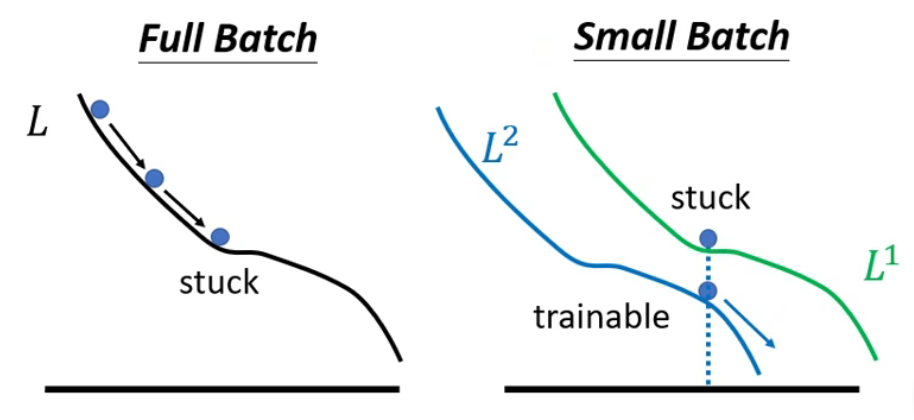
-
除了可以帮助
training,较小的batch还可能可以帮助testing。- 原因:当
Training Loss和Testing Loss之间有不匹配的地方,即两者的Loss函数不同(选取的样本不一样)。这样在testing的损失函数上,local minimum较平缓的最小值点比较陡峭的最小值点在training和testing的差别更小。大的batch size会让我们倾向于较为陡峭的最小值点,小的batch size会让我们倾向于较为平缓的最小值点。 Batch size是不得不去调整的超参数
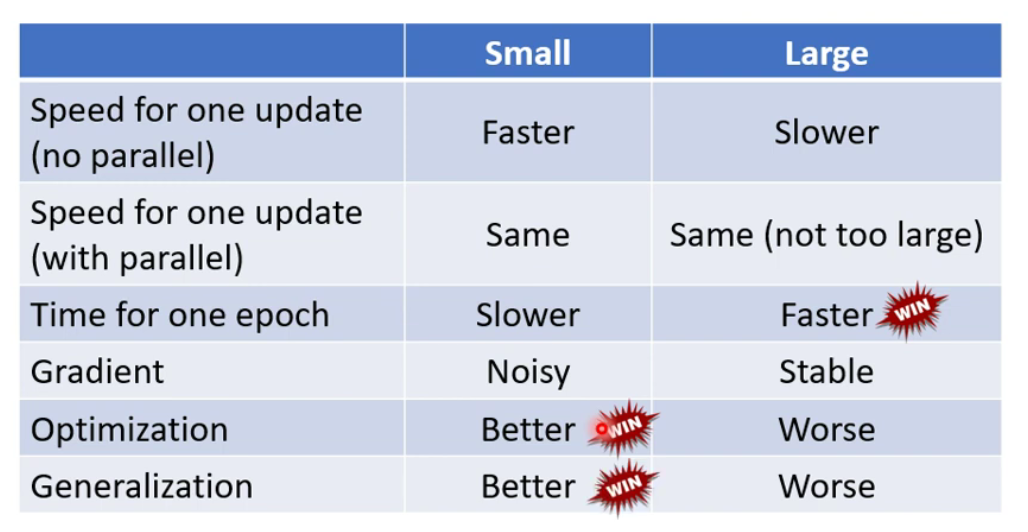
- 原因:当
-
-
Momentum-
背景:将Loss函数假象为真正的斜坡,参数想象成小球,在真实的物理世界中小球下降不一定会收到
saddle point和local minimum的阻拦。 -
一般的梯度下降
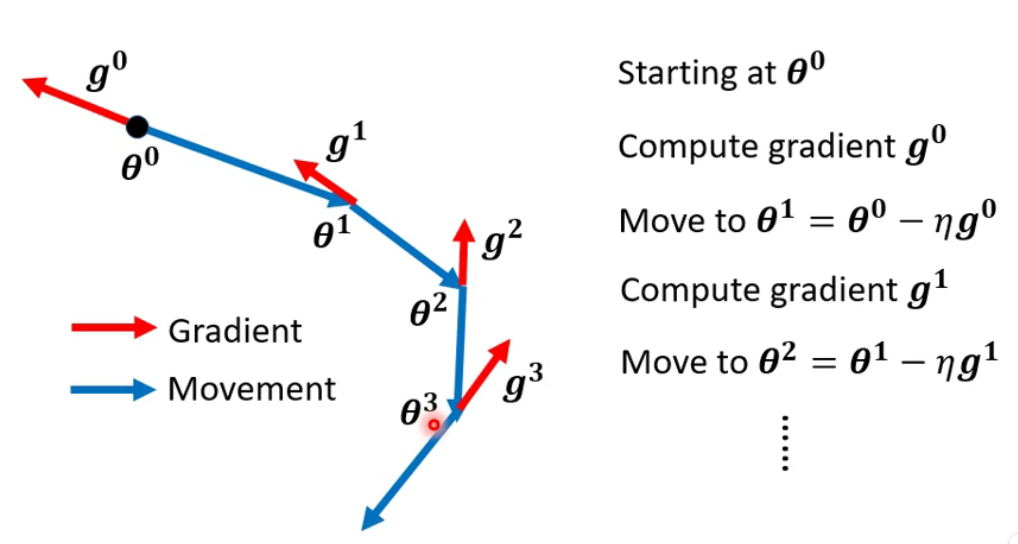
-
梯度下降加上动量
传统的梯度下降是向梯度的反方向移动参数。此时需要向梯度的反方向加上前一步移动的方向去移动参数。
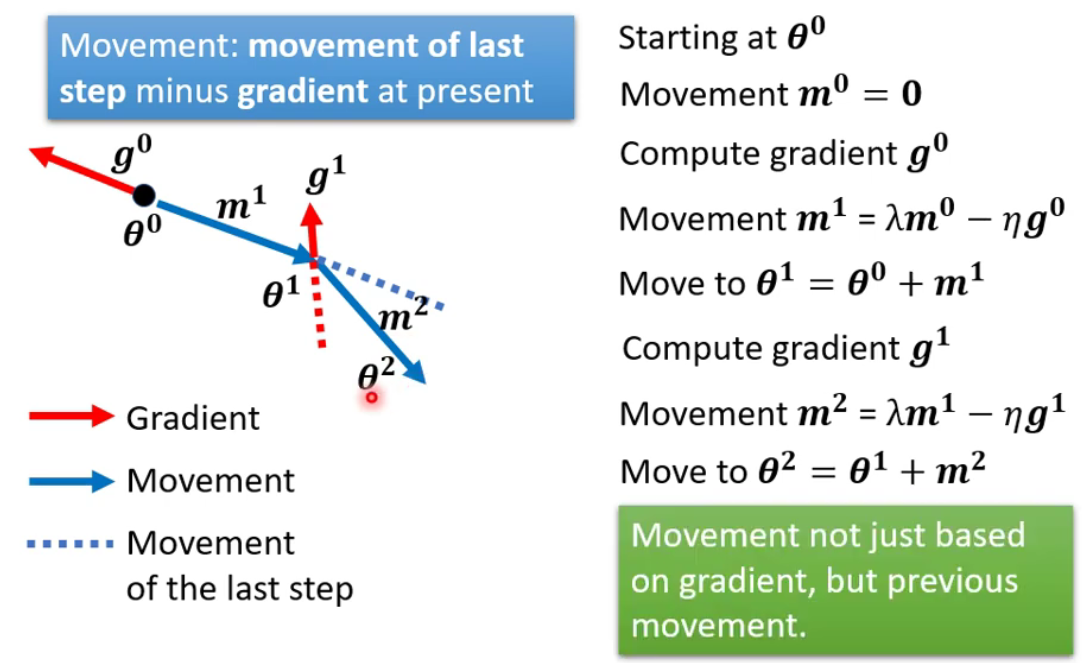
-
updata的方向不是考虑当前的梯度方向而是考虑过去所有的梯度总和
-
自动调整学习率(Learning Rate)
-
当Loss不再下降的时候,不一定卡在
Local minimum和saddle minimum,只是梯度确实无法继续下降了。 -
学习率产生的影响
- 当学习率较大时,梯度会来回震荡。当学习率较小时,梯度下降较慢,但在稍微平滑的地方就不再移动,无法到达
local minimum。 - 需要客制化学习率
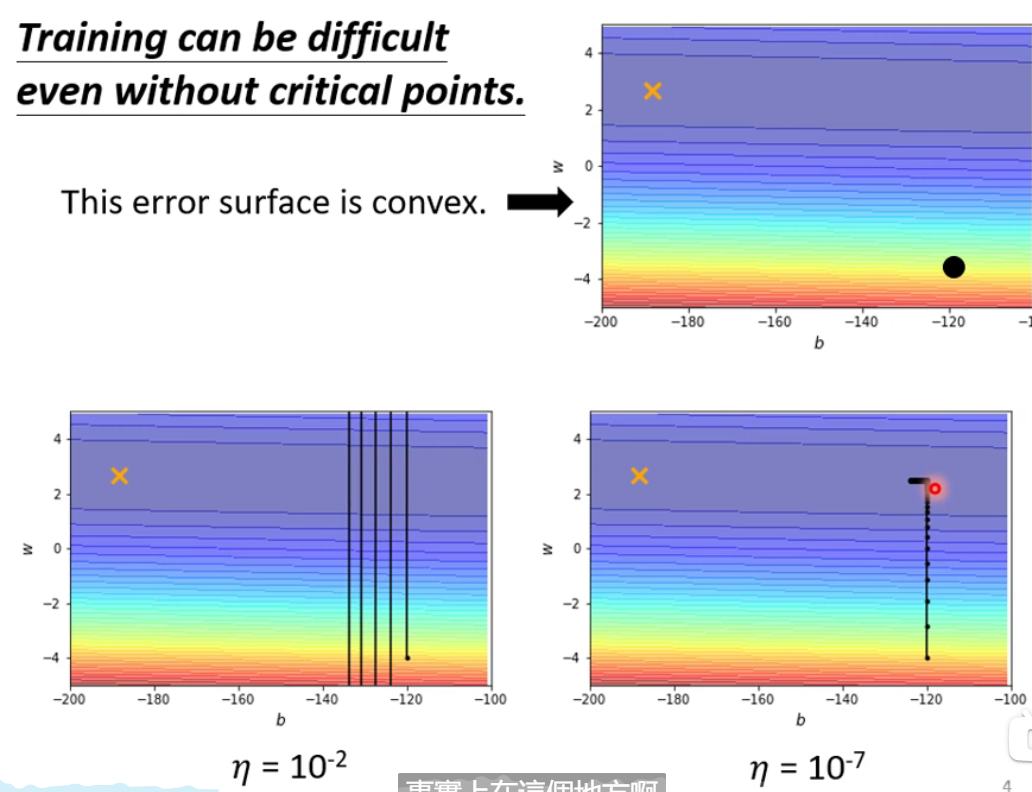
- 当学习率较大时,梯度会来回震荡。当学习率较小时,梯度下降较慢,但在稍微平滑的地方就不再移动,无法到达
-
改变梯度下降的公式,变为
Adagrad,当坡度小的时候,学习率就增大。坡度大的时候,学习率减小。原因:梯度小,对应均方根小,对应的学习率就变大。
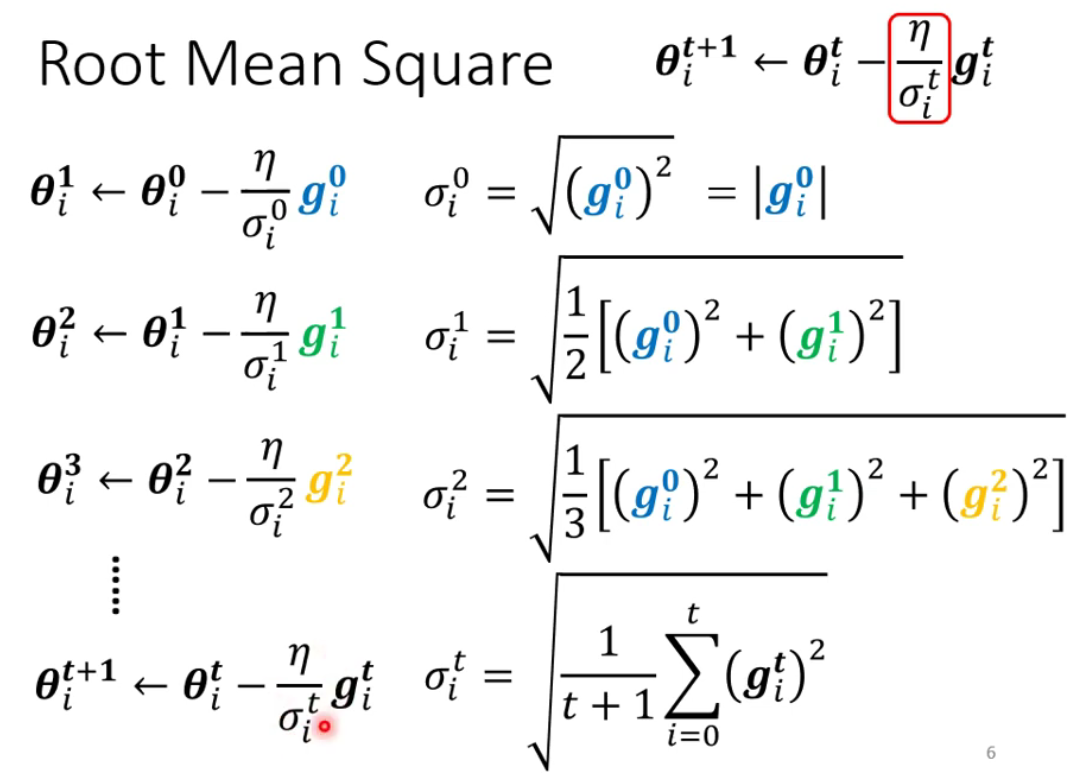
-
RMSProp(动态调整学习率)- 可以自由调整当前梯度的权重系数
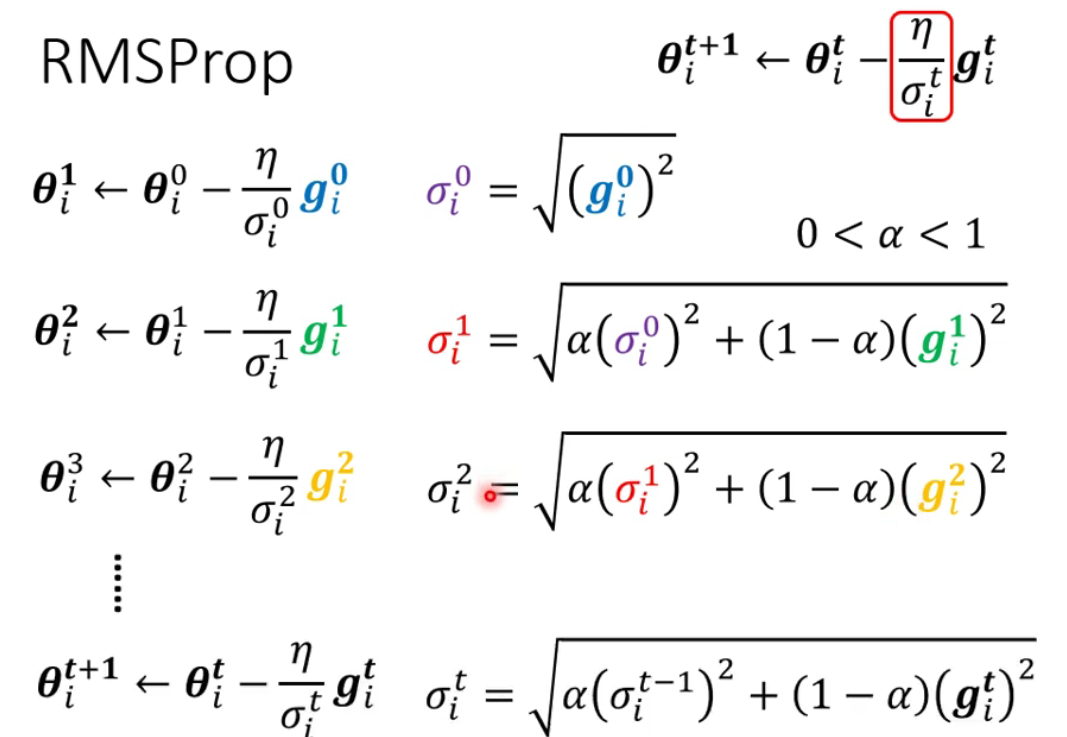
- 目前最常用的优化策略(optimization)是
Adam: RMSProp + Momentum
-
使用
Adagrad的表现: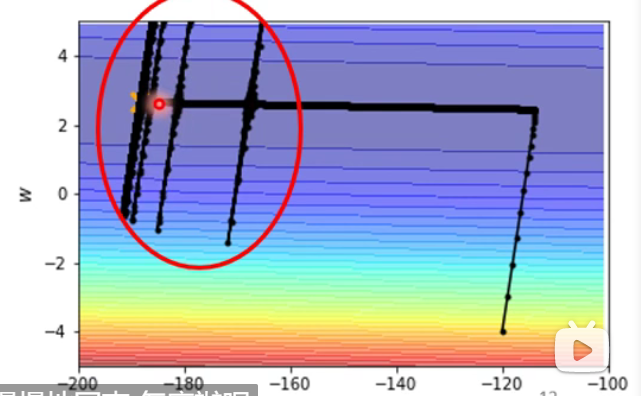
-
原因:在多个小均方根累积后会出现井喷式增长,但到梯度较大的地方又会返回。
-
解决方案:
Learning Rate Scheduling,将学习率预设为与时间有关。-
Learning Rate Decay:随着时间不断地进行,让学习率越来越小。
-
Warm Up:让学习率先变大后变小。
首先学习率较小,先收集有关均方根的数据,再让学习率爬升。
-
进一步了解
WarmUP
-
-
-
-
总结

分类与损失函数的影响
-
分类
-
分类标签标识的常见做法:将类别用
one-hot vector表示。 -
output如何输出成vector形式
-
回归得到的
y是数值型,而分类得到的y是一个向量,向量通过softmax得到最后的label。softmax就是将y(可以取任何值)的值限定于范围0到1之间
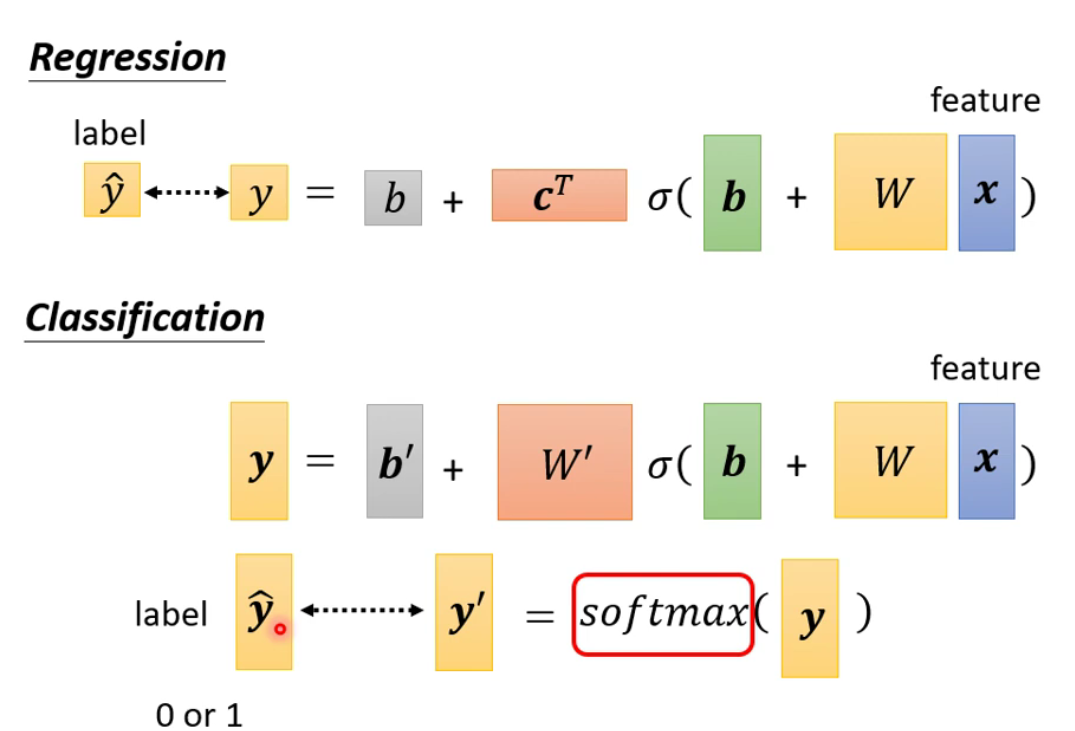
-
softmax的内部原理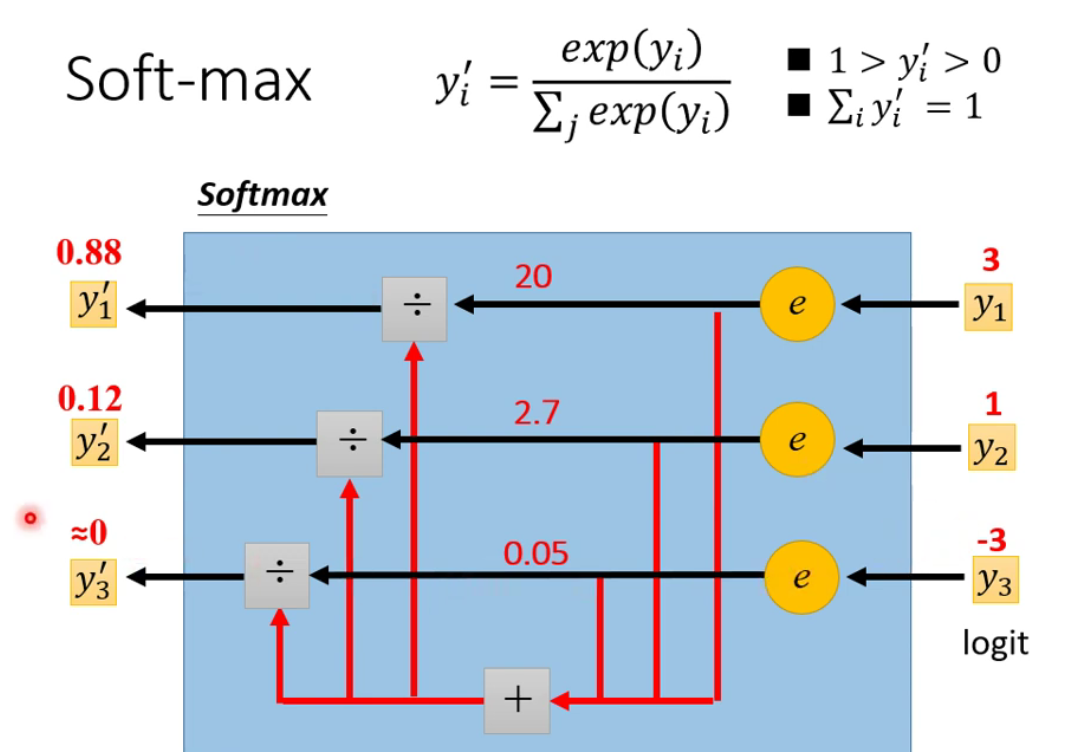
-
分类问题损失函数的计算
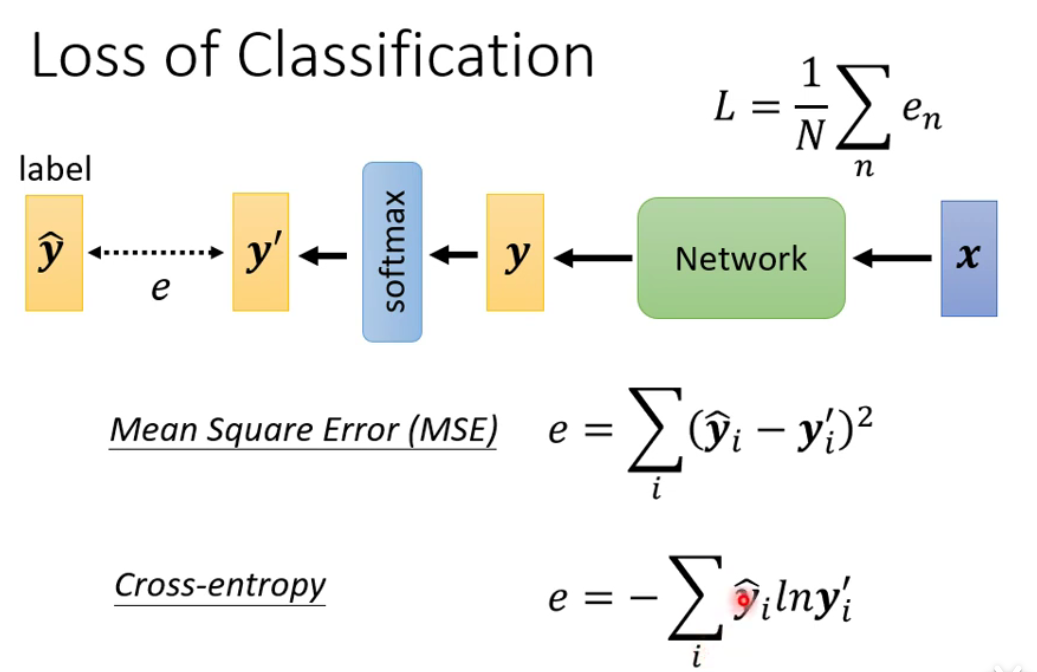
maximizing likelihood = minimizing cross-entropy最大似然估计和最小交叉熵是一件事
最小交叉熵比均方根更加适合用在分类问题上。
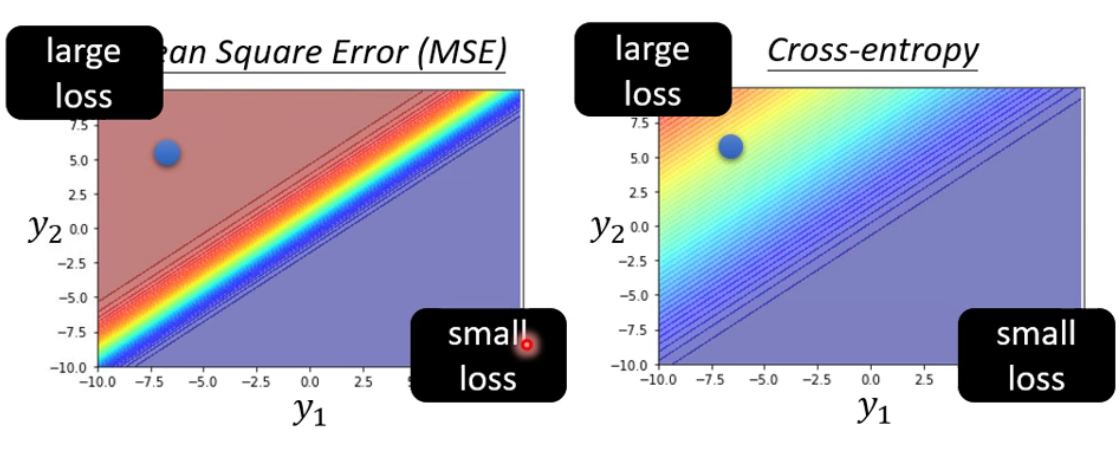
MSE在Loss较大的地方,梯度趋近于零,所以如果其初始位置在左上角,就很难通过梯度下降到达右下角。所以就算是损失函数的定义都可能影响training的过程。
-
批次标准化(Batch Normalization)
-
背景:想要直接改变
error surface的landscape,需要将特征值限定于相同的范围内,使得training过程更加容易。 -
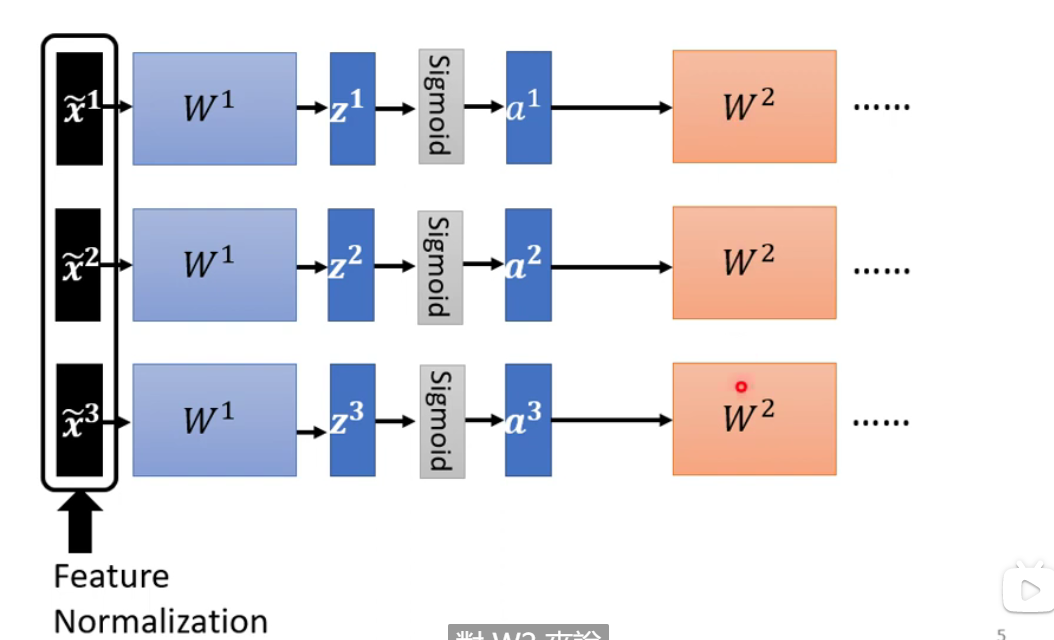
Feature Normalization-
做法:
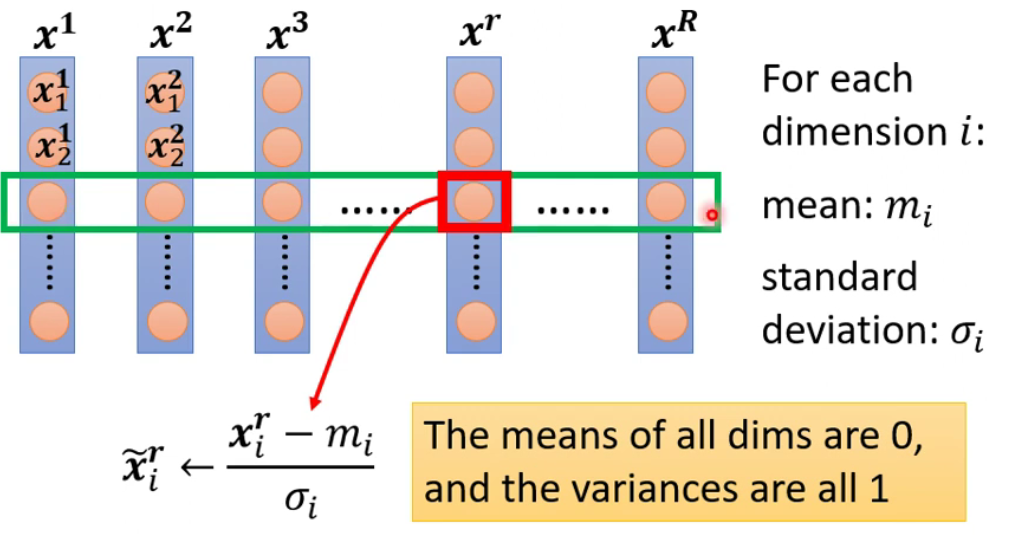
-
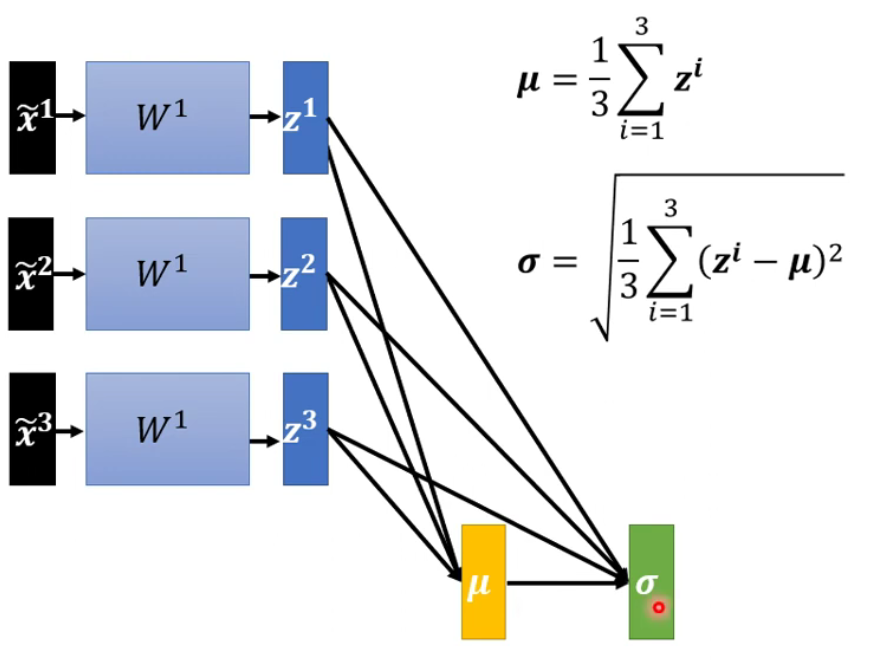
针对深度学习:通过相应层数之后的数值也需要进行标准化,在激活函数之前做还是在激活函数之后都可以。

-
由于现在
x决定z,z又决定a,可谓牵一发而动全身,所以当前需要将所有经历了标准化的变量过程当作network的一部分
GPU内存此时无法加载所有的data,所以在实践的时候只会考虑一个batch中的数据
-
下一步,
β和γ是另外被取出来的,是network的参数。原因是z~的平均值为0会对网络产生一些限制。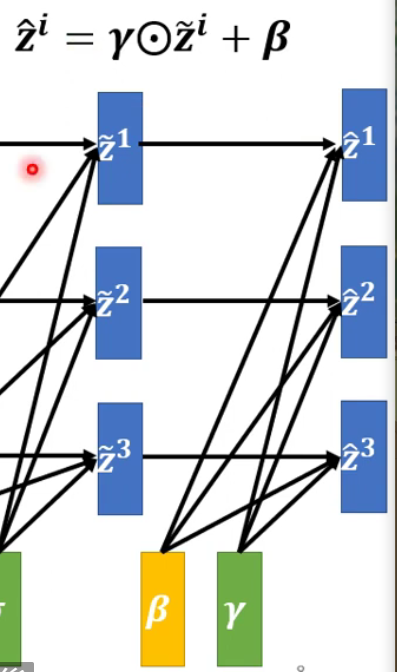
-


 浙公网安备 33010602011771号
浙公网安备 33010602011771号