AcWing 4957. 飞机降落 -- dfs

题目

有 \(N\) 架飞机准备降落到某个只有一条跑道的机场。

其中第 \(i\) 架飞机在 \(T_i\) 时刻到达机场上空，到达时它的剩余油料还可以继续盘旋 \(D_i\) 个单位时间，即它最早可以于 \(T_i\) 时刻开始降落，最晚可以于 \(T_i + D_i\) 时刻开始降落。

降落过程需要 \(L_i\) 个单位时间。

一架飞机降落完毕时，另一架飞机可以立即在同一时刻开始降落，但是不能在前一架飞机完成降落前开始降落。

请你判断 \(N\) 架飞机是否可以全部安全降落。

输入格式

输入包含多组数据。

第一行包含一个整数 \(T\)，代表测试数据的组数。

对于每组数据，第一行包含一个整数 \(N\)。

以下 \(N\) 行，每行包含三个整数：\(T_i\)，\(D_i\) 和 \(L_i\)。

输出格式

对于每组数据，输出 YES 或者 NO，代表是否可以全部安全降落。

数据范围

对于 \(30\%\) 的数据，\(N ≤ 2\)。
对于 \(100\%\) 的数据，\(1 ≤ T ≤ 10\)，\(1 ≤ N ≤ 10\)，\(0 ≤ T_i, D_i, L_i ≤ 10^5\)。

输入样例：

2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20

输出样例：

YES
NO

样例解释

对于第一组数据，可以安排第 \(3\) 架飞机于 \(0\) 时刻开始降落，\(20\) 时刻完成降落。安排第 \(2\) 架飞机于 \(20\) 时刻开始降落，\(30\) 时刻完成降落。安排第 \(1\) 架飞机于 \(30\) 时刻开始降落，\(40\) 时刻完成降落。

对于第二组数据，无论如何安排，都会有飞机不能及时降落。

题解

这道题数据范围非常小 \(1≤N≤10\) 所以我们采用dfs暴搜的方法 核心代码与基础课里dfs排列数字类似

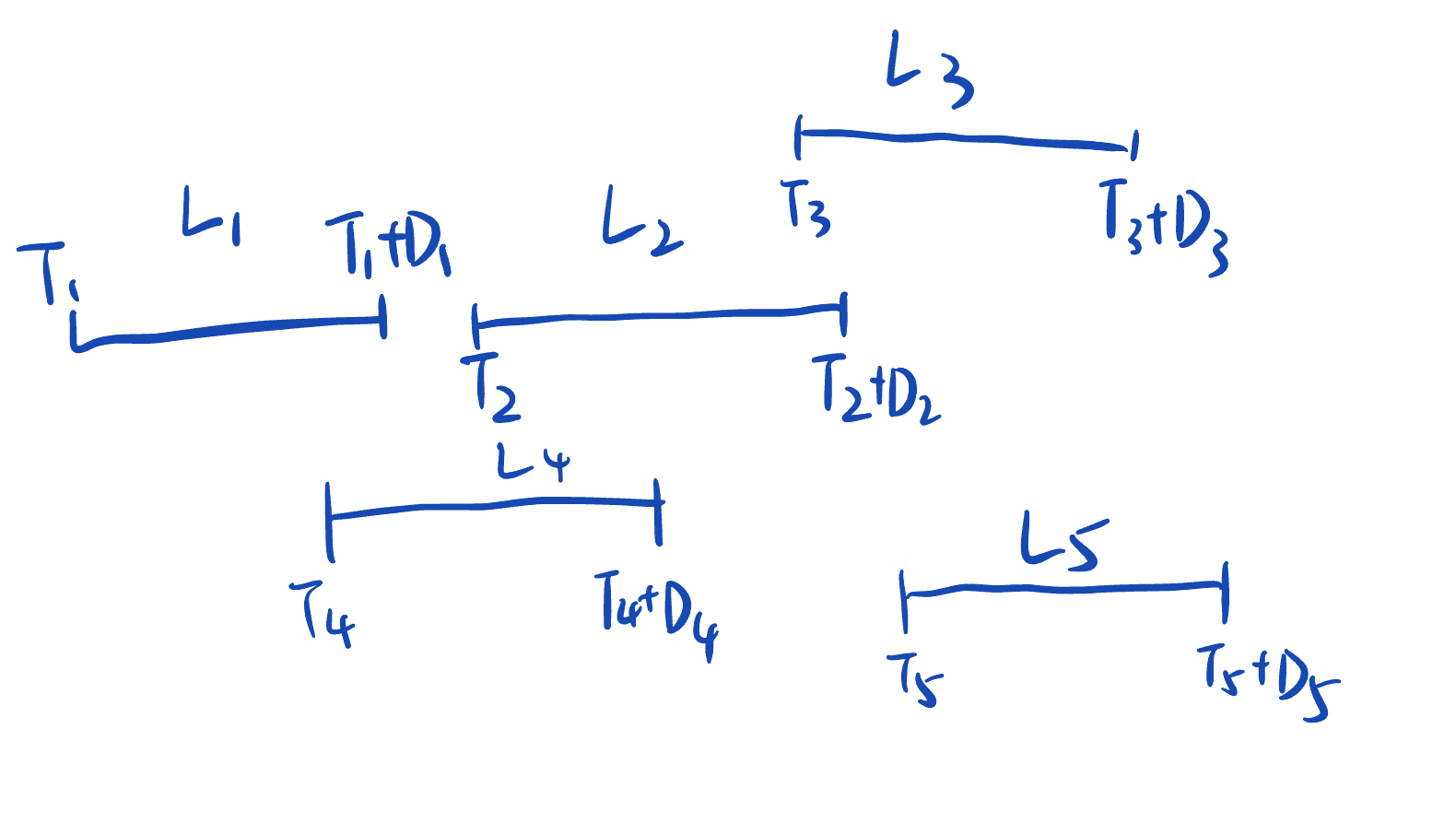
本质就是我们将这些无序的区间(表示飞机的到达时间T、最晚开始降落时间T+D、降落时间L) 像排列数字一样排列出不同的方案 选出其中能使所有区间均不重叠的方案，就能使全部飞机成功降落

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 15;

int n;
bool st[N]; //判断该飞机有没有降落

struct Plane //用结构体定义一架飞机的三个属性
{
    int t, d, l;
}p[N];

bool dfs(int u, int last) //u表示已经降落的飞机数量，last表示上一架飞机降落完成的时间
{
    if (u == n) return true; //u的范围是0~n-1 当u=n时，表示所有飞机已经降落

    for (int i = 0; i < n; i ++ )
    {
        int t = p[i].t, d = p[i].d, l = p[i].l;
        if (!st[i] && t + d >= last) //如果该飞机没有降落 并且 该飞机最晚降落时间 >= 上一家飞机降落时间
        {
            st[i] = true;
            if(dfs(u + 1, max(t, last) + l)) return true; //该飞机降落后向下搜索下一架飞机是否能降落 max(t, last)是取 上一架飞机降落时间 和 该飞机到达机场时间 取最大值，
                                                       // 目的是看该飞机最终是啥时候开始降落的(不能在上一架飞机降落时就降落也不能在还没到机场时就降落)再加上本次飞机降落时间l，就是本次飞机降落完成时间
                                                       //如果递归到dfs(n - 1, last)也能进入if(!st[i] && t + d >= last)(也就是最后一架飞机也可以正常降落) 那么if内我们就会递归到下一层dfs(n, last)最终u==n返回true
                                                       //返回到if(dfs(u + 1, max(t, last) + l))成立，继续return true，不断返回，最终返回到dfs(0, 0) 最终函数就会return true
            st[i] = false; //进行到这里表示上一句话没有return true 也就是下一架飞机不能降落 那么恢复现场，保证这架飞机可以在下一次for循环被继续利用
        }

    }
    return false; //如果循环内没有搜索到可以将全部飞机成功降落的顺序，就返回false
}

int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ )
        {
            int t, d, l;
            scanf("%d%d%d", &t, &d, &l);
            p[i] = {t, d, l};
        }
        memset(st, 0, sizeof st); //每次排列飞机降落顺序前都要把标记数组清空，防止被上一组数据影响(每次会测试很多组数据T)
        if (dfs(0, 0)) puts("YES"); //从已经降落的飞机数量为0 降落时间为0的点开始搜索
        else puts("NO");
    }

    return 0;
}