AcWing 5562. 最大生产----二分

题目

为了让所有奶牛的牛蹄都能得到及时修剪，约翰计划向某工厂定制一批自动修蹄车。

制作一辆修蹄车需要用到 \(n\) 种零件，其中第 \(i\) 种零件需要用 \(a_i\) 个。

由于约翰对于修蹄车数量的需求是越多越好，所以工厂也希望制作出尽可能多的修蹄车以满足客户的需求。

已知，对于第 \(i\) 种零件，工厂的库存为 \(b_i\) 个。

此外，工厂中还有 \(k\) 个未加工原材料，每个原材料都可以被加工为一个任意种类的零件。

请你计算，利用现有的零件以及原材料，工厂最多可以生产出多少辆修蹄车。

输入格式

第一行包含两个整数 \(n,k\)。

第二行包含 \(n\) 个整数 \(a_1,a_2,…,a_n\)。

第三行包含 \(n\) 个整数 \(b_1,b_2,…,b_n\)。

输出格式

一个整数，表示可以生产的修蹄车的最大可能数量。

数据范围

前 \(6\) 个测试点满足 \(1 \le n \le 10\)。
所有测试点满足 \(1 \le n \le 10^5\)，\(1 \le k \le 10^9\)，\(1 \le a_i,b_i \le 10^9\)。

输入样例1：

1 1000000000
1
1000000000

输出样例1：

2000000000

输入样例2：

10 1
1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
1 1 1 1 1 1 1 1 1 1

输出样例2：

0

输入样例3：

3 1
2 1 4
11 3 16

输出样例3：

4

输入样例4：

4 3
4 3 5 6
11 12 14 20

输出样例4：

3

---

题解

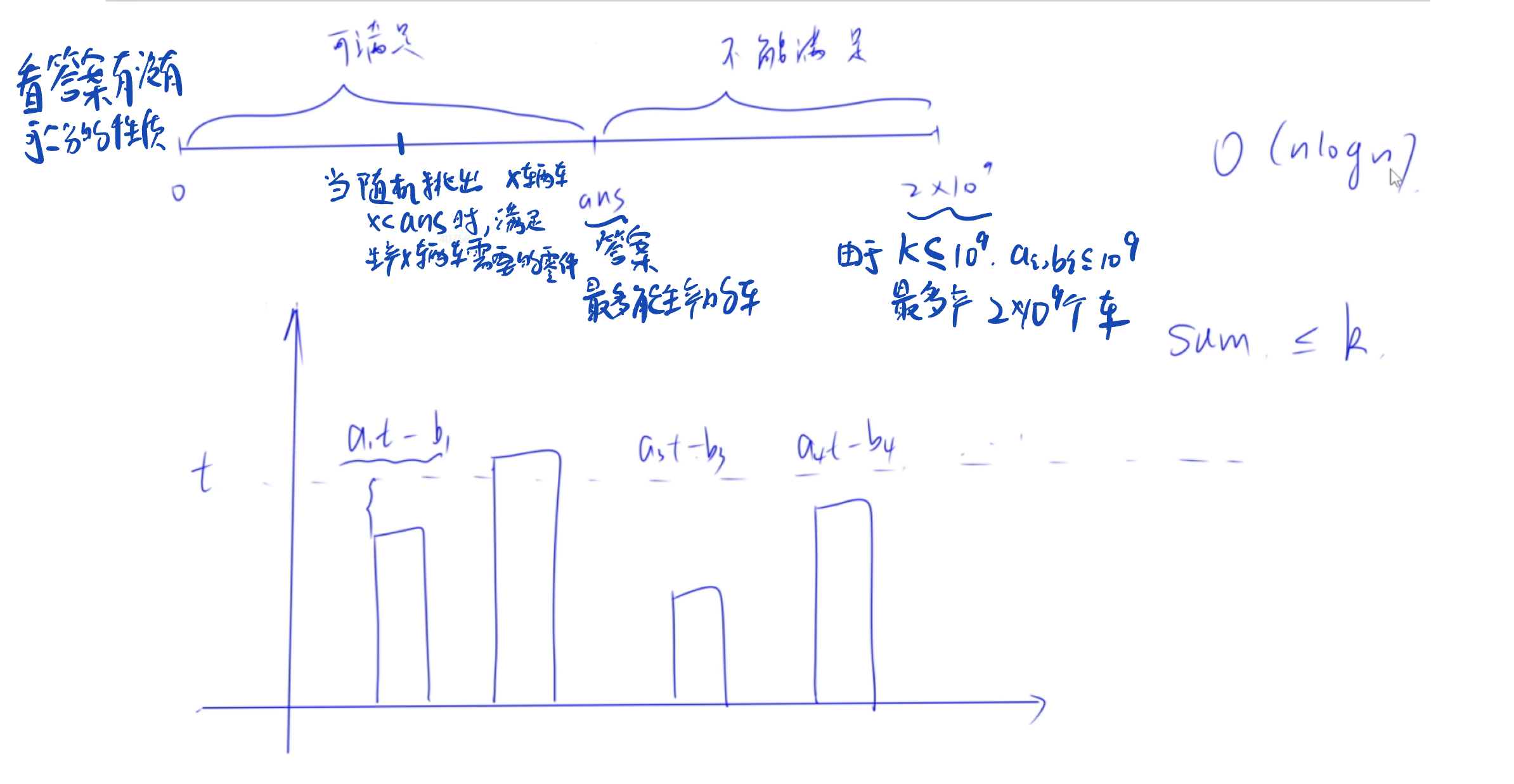
//int型范围差不多21亿
#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n, m;
int a[N], b[N];

bool check(int mid)
{
    LL res = 0;
    for (int i = 0; i < n; i ++ )
    {
        LL need = a[i] * (LL)mid;  //这里乘法可能溢出 我们要强转 强转加在可能爆int的运算的其中一个数据上
        if (need > b[i])
        {
            res += need - b[i];
            if (res > m) return false;
        }
    }
    return true;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]); //每种零件需要的数量
    for (int i = 0; i < n; i ++ ) scanf("%d", &b[i]); //每种零件的库存

    int l = 0, r = 2e9;  //边界范围
    while (l < r) //求右边界
    {
        int mid = l + (LL)r + 1 >> 1; //这里的l + r可能会溢出int 要强转LL
        if (check(mid)) l = mid;
        else r = mid - 1; //有加必有减
    }

    printf("%d\n", r);

    return 0;
}