洛谷 P2241. P2241 统计方形---暴力枚举

统计方形（数据加强版）

题目背景

1997年普及组第一题

题目描述

有一个 \(n \times m\) 方格的棋盘，求其方格包含多少正方形、长方形（不包含正方形）。

输入格式

一行，两个正整数 \(n,m\)（\(n \leq 5000,m \leq 5000\)）。

输出格式

一行，两个正整数，分别表示方格包含多少正方形、长方形（不包含正方形）。

样例 #1

样例输入 #1

2 3

样例输出 #1

8 10

---

题解

第一道暴力枚举的题 以为很简单 没写出来…
其实本题考察的是数学思维
我们怎么枚举一个正方形
利用图形内右下角坐标(i, j) i，j表示目前这个点 是长为i宽为j的的图形右下角
那么我们利用坐标(i, j)就明确了这个图形 当i == j 就说明这个图形是正方形
怎么计算当前这个以(i, j)作为右下角点的数量呢
以(2, 2)作为右下角的点的数量是(n - 2 + 1)(m - 2 + 1) 因为从右下角枚举 要加1

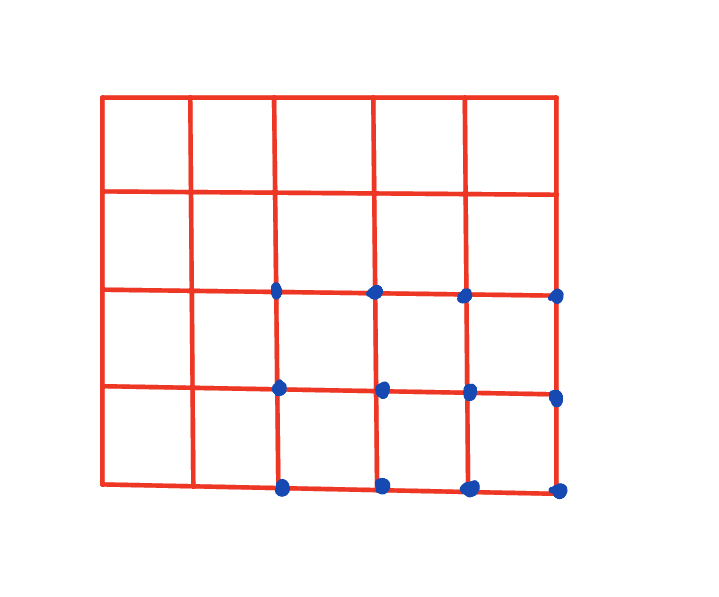
公式 以(i, j)为右下角的正方形数量为(n - i + 1)(m - j + 1)

---

长方形同理

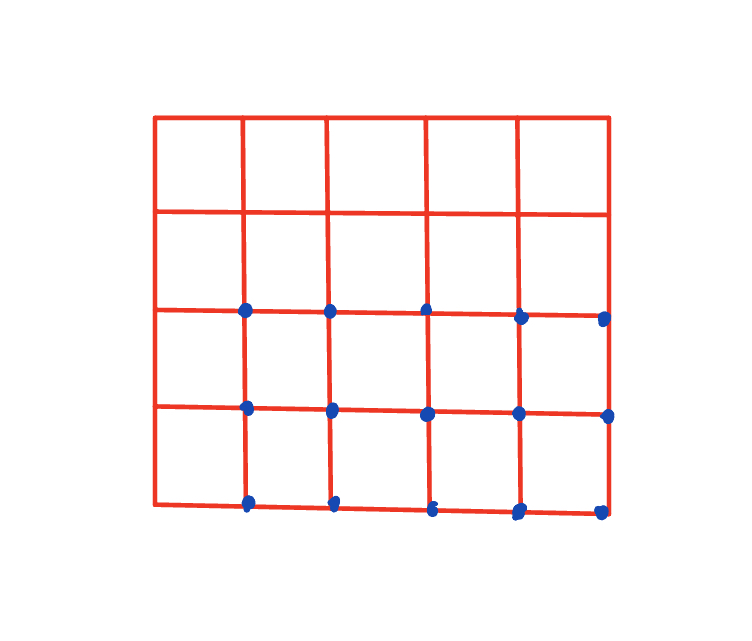
以(2, 1)为右下角的长方形数量为(n - 2 + 1)(m - 1 + 1)
公式 以(i, j)为右下角的长方形数量为(n - i + 1)(m - j + 1)
https://www.luogu.com.cn/article/u8t1hyks 更详细的公式解释

#include <bits/stdc++.h>

using namespace std;

int n, m;
long long cnt0, cnt1;

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) //由于从图形的右下角枚举 所以点的坐标至少是1 
    {
        for (int j = 1; j <= m; j ++ )
        {
            if (i == j) cnt0 += (long long)(n - i + 1) * (m - j + 1);
            else cnt1 += (long long)(n - i + 1) * (m - j + 1);
        }
    }

    printf("%lld %lld", cnt0, cnt1);

    return 0;
}