洛谷 P1149. 火柴棒等式 ---思路很重要 利用枚举和搜素两种方式

[NOIP2008 提高组] 火柴棒等式

题目描述

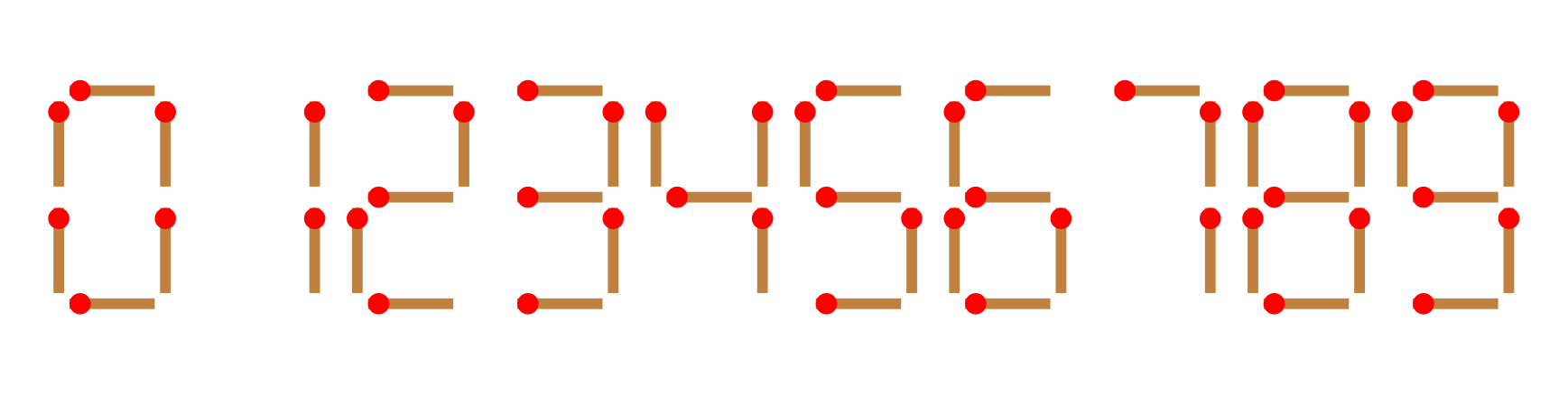
给你 \(n\) 根火柴棍，你可以拼出多少个形如 \(A+B=C\) 的等式？等式中的 \(A\)、\(B\)、\(C\) 是用火柴棍拼出的整数（若该数非零，则最高位不能是 \(0\)）。用火柴棍拼数字 \(0\sim9\) 的拼法如图所示：

注意：

1. 加号与等号各自需要两根火柴棍；
2. 如果 \(A\neq B\)，则 \(A+B=C\) 与 \(B+A=C\) 视为不同的等式（\(A,B,C\geq0\)）；
3. \(n\) 根火柴棍必须全部用上。

输入格式

一个整数 \(n(1 \leq n\leq 24)\)。

输出格式

一个整数，能拼成的不同等式的数目。

样例 #1

样例输入 #1

14

样例输出 #1

2

样例 #2

样例输入 #2

18

样例输出 #2

9

提示

【输入输出样例 1 解释】

\(2\) 个等式为 \(0+1=1\) 和 \(1+0=1\)。

【输入输出样例 2 解释】

\(9\) 个等式为

\(0+4=4\)、\(0+11=11\)、\(1+10=11\)、\(2+2=4\)、\(2+7=9\)、\(4+0=4\)、\(7+2=9\)、\(10+1=11\)、\(11+0=11\)。

noip2008 提高第二题

---

题解

这题的思路太巧妙了 我们只需要将所有数(2000以下)需要用多少根火柴棒给预处理出来
然后直接从0开始枚举a和b 等式右边的数就是a+b 这样就能将该等式的火柴棒数量算出来了
我们再找满足题目要求用满n根火柴棒的等式有多少个即可
核心代码
if (a[i] + a[j] + a[i + j] + 4 == n) cnt ++ ;

---

方法一 枚举

#include <bits/stdc++.h>

using namespace std;

int a[2001] = {6}; //我们用一个数组来记录 表示数字i需要的火柴棒数量
                   //注意这里{6} 是为了特殊处理数字0 因为下面的循环内算不了0 我们利用{6} 将数字0初始化为6 其余的数字i需要的火柴棒数量初始化为0
int n, cnt;
int c[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; //存一下0~9每个数字需要的火柴棒数量

int main()
{
    scanf("%d", &n); //读入拥有的火柴棒数量

    //开始计算数字1 ~2000需要的火柴棒数量
    for (int i = 1; i <= 2000; i ++ )
    {
        int j = i; //临时变量 确保i始终是当前数字的真实值 不会被循环内的操作改变 
        while (j >= 1)
        {
            //从数字i的最低位向最高位计算每一位需要的火柴棒数量 然后相加 
            a[i] = a[i] + c[j % 10]; //通过每次求i数字最低位上需要的火柴棒数量来计算总共需要的数量
            j /= 10; //除去已经计算过的最低位 
            //最高位计算完成后j==0 退出循环 
        }
    }
    for (int i = 0; i <= 1000; i ++ ) //循环数量够大就行 我们这里选的是1000+1000=2000这个等式作为最大值 
    {
        for (int j = 0; j <= 1000; j ++ )
        {
            if (a[i] + a[j] + a[i + j] + 4 == n) cnt ++ ; //关键一步！！我们直接在a数组内将其计算结果表示出来 这样就不用考虑前导0的问题 一定要记得加上+和=号的火柴棒数量 
        }
    }
    printf("%d\n", cnt);

    return 0;
}

---

方法二 更加通用
回溯搜索 (标准dfs模型)
和暴力枚举一样 也是利用代码
if (a[i] + a[j] + a[i + j] + 4 == n) cnt ++ ;
只不过我们是利用函数搜索 一个一个数搜索 搜索到等式的第三个数字时判断这行代码

#include <bits/stdc++.h>

using namespace std;

int x[1001] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; //初始化0 ~ 1000需要的火柴棒数量 并将0~9初始化题目的要求
int b[4]; //存构成一个等式的三个数分别所需的火柴棒数目 
int n, cnt;

void dfs(int l)
{
    //枚举构成等式三个数字中 当前函数所递归到的等式第l个数字的值 
    for (int i = 0; i <= 999; i ++ )
    {
        if (n - x[i] >= 0) //火柴棒数目够用
        {
            b[l] = i; //将构成等式的第l位数字所需火柴棒数目放入b数组 
            n = n - x[i]; //上一个等式数字消耗完后的剩余火柴棒数量 减去当前数字所需火柴棒数量 
            if (l == 3) //如果已经搜索到等式最后一位数字 
            {
                if(b[1] + b[2] == b[3] && n == 0) //如果满足题目要求 并且剩余火柴棒数量等于0
                    cnt ++ ; //方案数加1 
            }
            else dfs(l + 1); //若还未搜索到等式第三个数字 继续向下搜索
            n = n + x[i]; //恢复现场 保证回溯时剩余火柴棒数量没有被当前数字i影响 
        } 
    }
}

int main()
{
    scanf("%d", &n);
    n = n - 4; //先减去构成 +和=号 需要的火柴棒
    for (int i = 10; i <= 999; i ++ ) //预处理数i需要的火柴棒数量 由于本题数据量小 999预处理三位数已经够用 可以继续扩大 
    {
        x[i] = x[i % 10] + x[i / 10]; //这里非常巧妙！对于两位数分别计算其个位及第二位上的数需要的火柴棒  
                                      //当i++到三位数后 i%10计算其个位 i/10计算其第二位和第三位 一共两位数 由于前面两位数需要的火柴棒数目都计算出来了 所以这里x[两位数]可以直接加了
    }
    dfs(1); //从构成等式A+B=C的第一个数A开始搜 
    printf("%d\n", cnt);
    return 0;
}