洛谷 P3799. 小Y拼木棒 --- 排列与组合数的表示 暴力枚举

小 Y 拼木棒

题目背景

上道题中，小 Y 斩了一地的木棒，现在她想要将木棒拼起来。

题目描述

有 \(n\) 根木棒，现在从中选 \(4\) 根，想要组成一个正三角形，问有几种选法？

答案对 \(10^9+7\) 取模。

输入格式

第一行一个整数 \(n\)。

第二行往下 \(n\) 行，每行 \(1\) 个整数，第 \(i\) 个整数 \(a_i\) 代表第 \(i\) 根木棒的长度。

输出格式

一行一个整数代表答案。

样例 #1

样例输入 #1

4 
1
1
2
2

样例输出 #1

1

提示

数据规模与约定

• 对于 \(30\%\) 的数据，保证 \(n \le 5 \times 10^3\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n \le 10^5\)，\(1 \le a_i \le 5 \times 10^3\)。

关于标题：因为一些不可抗力的原因，名称进行了更改。深表歉意。

题解

---

题解

我们要从n根木棒里选4根出来 拼成一个等边三角形
刚开始都看错题意了 选出来的四根是必须要求能拼成一个等边三角形的
关键点就是这个四根木棒拼成等边三角形
若能拼成 必然存在: 两根长度相等 且另外两根木棒长度之和等于前两根木棒的长度
太妙了我只能说 不论你是用两根木棒凑成三角形的一条边 还是一根木棒单独作为一条边 都是符合这个结论的
好了 接下来就枚举吧 分别枚举这两种木棒的长度 记录方案数

来自 https://www.luogu.com.cn/article/5zvy12ri
我们来回顾一下组合数怎么求

所以

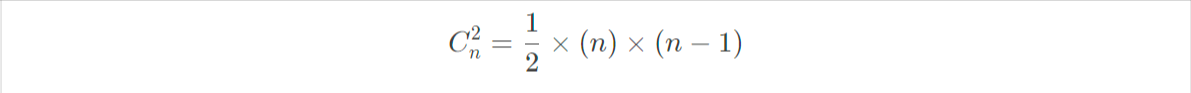
来自 https://www.luogu.com.cn/article/6p9hbrbq
现在我们把每层循环要干啥给搞清楚了 就可以开始实现代码了
注意计算过程中随时都要取mod 避免哪一环就给溢出了
也是debug了一会儿 像这种代码多的 就有很多细节 感觉也是debug量积累起来 才能一眼就看出的
以后代码提交ac不了 先留五分钟自己检查代码哪里出问题了 再去看答案 这也是对代码是否理解的一个考察

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10, mod = 1e9 + 7;

typedef long long LL;

int n, a[N], num[N]; //nums数组存的是长度为i的木棒有多少根 
int maxa; //我们需要记录最长的木棒长度大小 用来开枚举长度的边界 
LL times, ans; //times存枚举前两根木棒的组合情况 ans记录取出全部木棒的组合情况 

LL C(int x, int y) //求组合数的函数 
{
    if (y == 1) return x % mod; //取出一个数的情况 
    if (y == 2) return (x * (LL)(x - 1) / 2) % mod; //取出两个数的情况 
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ )
    {
        scanf("%d", &a[i]);
        num[a[i]] ++ ; //a[i]长度的木棒个数++
        maxa = max(maxa, a[i]); 
    } 

    for (int i = 1; i <= maxa; i ++ ) //枚举两根长度相等的木棒 
    {
        if (num[i] >= 2) //确保当前枚举到的长度 存在着至少两根木棒
        {
            times = C(num[i], 2) % mod; //先求出从所有长度为i的木棒中取出2根的组合数
            for (int j = 1; j <= i / 2; j ++ ) //j只用枚举到2/i即可 后面的用i-j去表示 要不然会重复
            {
                if (j == i - j && num[j] >= 2) //如果剩下两根长度相等 那我们只需要从长度为j的木棒中取两根出来即可 
                {
                    ans += (times * C(num[j], 2)) % mod;
                    //cout << ans << endl;
                }
                if (j != i - j && num[i - j] >= 1 && num[j] >= 1) //如果剩下两根长度不一致 那我们就分别从长度为j和长度为i-j的木棒里取一根出来 再将其组合数相乘 这两根木棒的个数要求也只需要比一根多即可 
                {
                    ans += (times * C(num[i - j], 1) * C(num[j], 1)) % mod;
                    //cout << ans << endl;
                }
                ans %= mod; //ans+=之后也可能溢出 在这里也mod一下 
            }
        }
    }

    printf("%lld", ans);

    return 0;
}