树的重心、点分治学习笔记

树的重心常常作为一种优化复杂度的好工具，同时其优秀的性质给一些并不可做的题目提供了许多思路。

而点分治正是运用了树的重心的算法，通常用于处理带权路径统计问题。

树的重心

一.定义

找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心。

~~它还有个很丑的名字叫树的最大独立集。~~

那么我们的思路就很清晰了:
通过树形dp计算出各个子树的结点值，维护一个Max[x]表示删除x结点后的最大子树。转移方程如下：

\[Max_{u∈son[x]} ({Max[u],sum-Max[u])} \]

代码如下：

#define REP(i,x) for(int i=(head[x]);i;i=(nxt[i]))
int siz[N],Sum,Max[N];
int root;

void dfs1(int x,int fa){
    siz[x]=1;Max[x]=0;
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        dfs1(u,x);siz[x]+=siz[u];
        Max[x]=std::max(Max[x],siz[u]);//更新当前子树的最大结点数
    }
    Max[x]=std::max(Max[x],Sum-siz[x]);//更新最大子树
    if(Max[x]<Max[root]) root=x;//更新最少结点
}

二.性质

\(\texttt{1.与数学概念相似，树的重心到树的各结点的距离和最小。}\)

☆ \(\texttt{2.重心所在子树的大小不超过整个树大小的一半。}\)

\(\texttt{3.添加或删除一个子结点，整个树的重心至多移动一条边的距离。}\)

☆\(\texttt{4.一棵树至少有两个重心。}\)

三.例题

\(\texttt{CF685B Kay and Snowflake}\)

一句话题意：

求出每一个子树的重心。

\(N\le3e5\)

\(Solution\)

讨论一下。

对于叶结点的重心一定是自己。

对于一个普通的子树，重心一定落在重链上。

对于一个子树大小超过了整个树一半的情况，直接pass。

但是复杂度明显和普通枚举没两样，我们考虑优化。

在已判定\(i\)结点不是结点后，我们不断向上递归，直到找到该子树的重心为止。

复杂度是优秀的\(O(n)\)，代码和树剖特别像，注意预处理重儿子。

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define N 500005
#define rep(i,l,k) for(int i=(l);i<=(k);i++)
int siz[N],nxt[N],head[N],to[N],son[N],fa[N],dep[N],ans[N],n,q,cnt;
void Add(int u,int v){nxt[++cnt]=head[u];head[u]=cnt;to[cnt]=v;}
int ip(){int x=0,w=0;char ch=0;while(!isdigit(ch)) w|=ch=='-',ch=getchar();while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();return w?-x:x;}
inline void dfs1(int x){
    siz[x]=1;for(int i=head[x];i;i=nxt[i]){
    int u=to[i];fa[u]=x;dep[u]=dep[x]+1;dfs1(u);siz[x]+=siz[u];
    if(siz[u]>siz[son[x]]) son[x]=u;
    }
}
inline void dfs2(int x){
    if(!son[x]) {ans[x]=x;return;}
    for(int i=head[x];i;i=nxt[i]) dfs2(to[i]);
    if((siz[son[x]]*2<=siz[x])) {ans[x]=x;return;}
    for(int i=ans[son[x]];i!=x;i=fa[i]) if(max(siz[son[i]],siz[x]-siz[i])*2<=siz[x]) {ans[x]=i;break;}
}
int main(){
    n=ip(),q=ip();rep(i,2,n){Add(ip(),i);}
    dfs1(1);dfs2(1);rep(i,1,q){printf("%d\n",ans[ip()]);}
    return 0;
}

因此这道题可以加强到\(3e7\)，但是可能会卡完全二叉树?

~~FJOI2014那题不会写。~~

点分治

一.定义

用来处理树上路径问题。
比如P3806的树上距离为k的点对问题。

二.例题

\(\texttt{P3806 【模板】点分治1}\)

题目描述：

给定一棵有\(n\)个点的树

询问树上距离为\(k\)的点对是否存在。

数据范围：

\(n\le1e4\) , \(m\le1e2\) , \(k\le1e7\)

\(Solution\)

显然暴力枚举就是\(n^2\)。极限操作是可以过的。

点分治的作用就出现了。

\(1.\)点分治的实质是将一棵树剖分成若干棵子树进行分治处理。
\(2.\)对于一棵树上的区间和，我们的选点影响着复杂度。

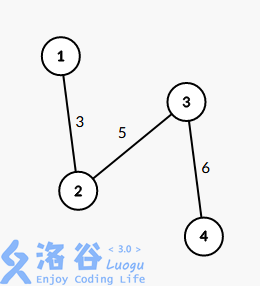
(一条被分治的链)

如图，选择\(1\)点遍历就是\(O(n)\),选择越里层的点，那么复杂度越低，最优复杂度即为\(O(logn)\)

\(3.\)树的重心引入。

现在我们假设剖分第\(i\)棵树，我们要使得遍历这棵树及其子树是最优复杂度，恐怕并不好抉择。

那我们放大到整棵树，为了保持最优性，我们要找到一个点，以之作为遍历初始点，遍历整棵树的总路径是最小的。

根据树的重心性质\(1\)有，树的重心到树的各结点的距离和最小。

那么显然，结论就是：点分治过程中，以树的重心作为子树的树根，遍历深度是不会超过\(logn\)层的（整棵树深度）.

复杂度证明结束，为\(O(nlogn)\)。

4.准备工作：求出距离。

很常规的写法，新开数组存储新边的权值。

代码如下：

void get_dis(int x,int len,int fa){
    dis[++tot]=a[x];
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        a[u]=len+val[i];get_dis(u,len+val[i],x);
    }
}

\(5.\)分治主过程

在分治某一棵树的过程中，经常会重复计算。

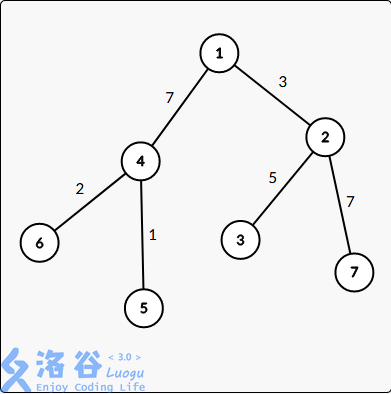
路径分治计算过程是那么执行的：

1->2 1->4

1->2->3 1->2->7

1->4->6 1->4->5

最后总的路径叠加即是我们的计算答案。

我们发现一些事情：结点\(2\)、\(4\)被计算了两次。

为了删去答案，我们要减去\(to[i]\)的贡献。

代码如下：

int head[N],vis[N],to[N],nxt[N],Sum,root,Max[N];
#define REP(i,x) for(int i=head[x];i;i=nxt[i])

void get_rt(int x,int fa){
    ...
}
int solve(int x,int len,int w){
    ...
}
void Divide(int x){
    solve(x,0,1);//算上树根的贡献
    vis[x]=1;
    REP(i,x){
        int u=to[i];if(vis[u]) continue;
        solve(u,val[i],-1);//删去多余贡献
        Sum=siz[x];root=0;Max[0]=n;get_rt(u,x);//以x为新树树根，求一次树的重心
        Divide(root);
    }
}

-\(6.\) \(Solve\)函数?

Solve函数是对一颗子树的操作。

函数内容因题而异，因此接下来的例题我大多只强调\(Solve()\)的内容。

对于这道题，我们是这么写的。

void solve(int s,int len,int w){
    tot=0;a[s]=len;get_dis(s,len,0);
    rep(i,1,tot) rep(j,1,tot) if(i!=j) ans[dis[i]+dis[j]]+=w;
}

关键就是：暴力枚举所有点的距离。最后判断一下求出的距离ans[i]是否为k。

总代码如下：

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
#define N 10005
#define M 1000005
#define rep(i,l,k) for(int i=(l);i<=(k);i++)
int siz[N],head[N],nxt[M],to[M],val[M],Max[N],vis[M],n,m,cnt,Sum,root;
#define REP(i,k) for(int i=head[k];i;i=nxt[i])
void Add(int u,int v,int w){nxt[++cnt]=head[u];head[u]=cnt;to[cnt]=v;val[cnt]=w;}
int ip(){
    int x=0,w=0;char ch=0;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return w?-x:x;
}
void get_rt(int x,int fa){
    siz[x]=1;Max[x]=0;
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        get_rt(u,x);siz[x]+=siz[u];
        Max[x]=max(Max[x],siz[u]);
    }
    Max[x]=max(Max[x],Sum-Max[x]);
    if(Max[x]<Max[root]) root=x;
}
int que[M],ans[M],dis[M],a[M],tot;
void get_dis(int x,int len,int fa){
    dis[++tot]=a[x];
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        a[u]=len+val[i];get_dis(u,len+val[i],x);
    }
}
void out(int s,int len,int w){
    tot=0;a[s]=len;get_dis(s,len,0);
    rep(i,1,tot) rep(j,1,tot) if(i!=j) ans[dis[i]+dis[j]]+=w;
}
void divide(int x){
    out(x,0,1);vis[x]=1;
    REP(i,x){
        int u=to[i];if(vis[u]) continue;
        out(u,val[i],-1);
        Sum=siz[x];root=0;Max[0]=n;get_rt(u,x);
        divide(root);
    }
}
void Gao(){Sum=n;Max[0]=n;root=0;get_rt(1,0);divide(root);}
bool judge(int x){return ans[x]?1:0;}
int main(){
    n=ip(),m=ip();
    rep(i,1,n-1){int x,y,z;x=ip(),y=ip(),z=ip();Add(x,y,z);Add(y,x,z);}
    Gao();
    rep(i,1,m){puts(judge(ip())?"AYE":"NAY");}
    return 0;
}

\(\texttt{P4178 Tree}\)

题目让你求出树上距离小于等于\(k\)的点对有多少个。

\(n\le4e4\)

\(Solution\)

看起来和上面一题没啥区别。

实际真的没啥区别。

改一下\(solve()\)函数。

int solve(int s,int len,int w){
    tot=0;a[s]=len;get_dis(s,len,0);
    sort(dis+1,dis+1+tot);int l=1,r=tot,ans=0;
    while(l<=r) {if(dis[l]+dis[r]<=k) ans+=r-l,++l;else --r;}
    return ans;
}

看着像二分其实是个夹逼的过程，说白了还是暴力（摊手）。

代码如下：

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
#define N 40005
#define M 80005
#define rep(i,l,k) for(int i=(l);i<=(k);i++)
int siz[N],head[N],nxt[M],to[M],val[M],Max[N],vis[M],n,m,cnt,Sum,root,k;
#define REP(i,k) for(int i=head[k];i;i=nxt[i])
void Add(int u,int v,int w){nxt[++cnt]=head[u];head[u]=cnt;to[cnt]=v;val[cnt]=w;}
int ip(){
    int x=0,w=0;char ch=0;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return w?-x:x;
}
void get_rt(int x,int fa){
    siz[x]=1;Max[x]=0;
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        get_rt(u,x);siz[x]+=siz[u];
        Max[x]=max(Max[x],siz[u]);
    }
    Max[x]=max(Max[x],Sum-Max[x]);
    if(Max[x]<Max[root]) root=x;
}
int Ans,dis[M],a[M],tot;
void get_dis(int x,int len,int fa){
    dis[++tot]=a[x];
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        a[u]=len+val[i];get_dis(u,len+val[i],x);
    }
}
int out(int s,int len,int w){
    tot=0;a[s]=len;get_dis(s,len,0);
    sort(dis+1,dis+1+tot);int l=1,r=tot,ans=0;
    while(l<=r) {if(dis[l]+dis[r]<=k) ans+=r-l,++l;else --r;}
    return ans;
}
void divide(int x){
    Ans+=out(x,0,1);vis[x]=1;
    REP(i,x){
        int u=to[i];if(vis[u]) continue;
        Ans-=out(u,val[i],-1);
        Sum=siz[x];root=0;Max[0]=n;get_rt(u,x);
        divide(root);
    }
}
void Gao(){Sum=n;Max[0]=n;root=0;get_rt(1,0);divide(root);}
int main(){
    n=ip();
    rep(i,1,n-1){int x,y,z;x=ip(),y=ip(),z=ip();Add(x,y,z);Add(y,x,z);}
    k=ip();Gao();
    printf("%d",Ans);
    return 0;
}

\(\texttt{P2634 [国家集训队] 聪聪可可}\)

题意：

选择两个点，求出两个点之间所有边权值和为3的倍数的概率。

\(Solution\)

~~我寻思国集题那么喜欢求概率的吗。~~

设p[1]、p[2]、p[3]分别为权值1,2,3的数量。

由乘法原理有，正好组成权值三的概率为：

\(p[1]*p[1]+p[2]*p[3]+p[3]*p[2]\)

即\(p[1]^2+2*p[2]*p[3]\)

那么\(Solve\)函数如下：

int solve(int s,int len){
    a[s]=len;p[0]=p[1]=p[2]=0;get_dis(s,0);
    return (p[0]*p[0]+p[1]*p[2]*2);
}

代码如下：

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
#define N 20005
#define M 1000005
#define rep(i,l,k) for(int i=(l);i<=(k);i++)
int siz[N],head[N],nxt[M],to[M],p[5],val[M],Max[N],vis[M],n,m,cnt,Sum,root,ans;
#define REP(i,k) for(int i=head[k];i;i=nxt[i])
void Add(int u,int v,int w){nxt[++cnt]=head[u];head[u]=cnt;to[cnt]=v;val[cnt]=w;}
int ip(){
    int x=0,w=0;char ch=0;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return w?-x:x;
}
int gcd(int a,int b){return b==0?a:gcd(b,a%b);}
void get_rt(int x,int fa){
    siz[x]=1;Max[x]=0;
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        get_rt(u,x);siz[x]+=siz[u];
        Max[x]=max(Max[x],siz[u]);
    }
    Max[x]=max(Max[x],Sum-Max[x]);
    if(Max[x]<Max[root]) root=x;
}
int a[M];
void get_dis(int x,int fa){
    p[a[x]%3]++;
    REP(i,x){
        int u=to[i];if(u==fa||vis[u]) continue;
        a[u]=a[x]+val[i];get_dis(u,x);
    }
}
int out(int s,int len){
    a[s]=len;p[0]=p[1]=p[2]=0;get_dis(s,0);
    return (p[0]*p[0]+p[1]*p[2]*2);
}
void divide(int x){
    ans+=out(x,0);vis[x]=1;
    REP(i,x){
        int u=to[i];if(vis[u]) continue;
        ans-=out(u,val[i]);
        Sum=siz[u];root=0;get_rt(u,x);
        divide(root);
    }
}
void Gao(){Sum=n;Max[0]=n+1;root=0;get_rt(1,0);divide(root);}
int main(){
    n=ip();
    rep(i,1,n-1){int x,y,z;x=ip(),y=ip(),z=ip()%3;Add(x,y,z);Add(y,x,z);}
    Gao();
    printf("%d/%d",ans/gcd(ans,n*n),n*n/gcd(ans,n*n));
    return 0;
}

posted @ 2022-01-07 13:29 SxtoxA 阅读(168) 评论(0) 收藏举报

刷新页面返回顶部

MrWangnacl

AFO, Data Science，Computer Science.

树的重心、点分治学习笔记

树的重心

一.定义

二.性质

三.例题

点分治

一.定义

二.例题

题目描述：

数据范围：

公告