（整活）如何用微积分来求出圆锥的体积

众所不周知，小美在小学的时候就已经学过圆锥的体积是它同高同底面积的圆柱的\(\frac{1}{3}\)。

但是该怎么证明呢？这始终是小美心中的一个结（因为小美早就忘记了当初小学老师的是怎么教他证的了）。

于是他想啊想啊，忽地，他决定从体积\(V\)的定义开始入手。

那么什么是体积\(V\)呢？相信学过体积的都知道体积\(V\)=\(hS\)，其中我们先假设这个体积\(V\)表示的是一个规则的物体（例如正方体长方体等）。那如果以\(S\)为\(y\)轴，以\(h\)为\(x\)轴，建立一个平面直角坐标系，\(V\)代表的意义又是什么呢？

心灵手巧的小美果断画了画：

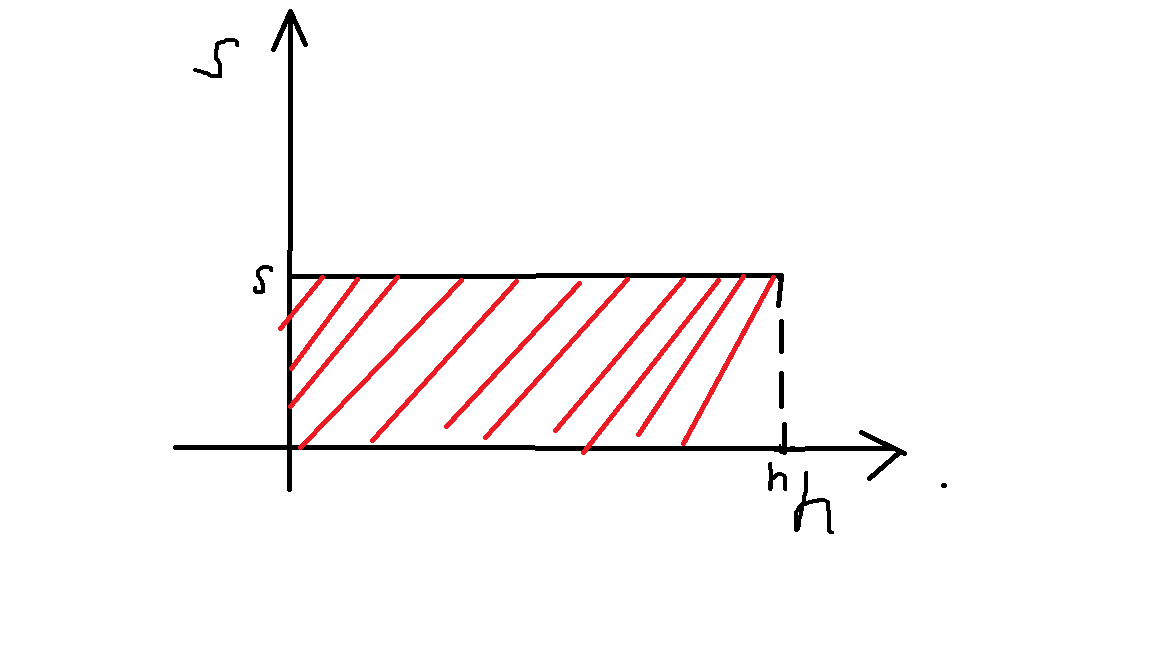
忽略小美画的斜斜的难看的图像（心不灵手不巧）。好啦，他现在已经得到了高为\(h\)，底面积为\(S\)的一个规则的物体\(h-S\)图像，嗯······那么\(V\)的意义就是红色阴影的面积。
好啦，现在小美似乎找到了表示圆锥的\(h-V\)图像的方法：
仅需知道圆锥的高（h）和圆锥在此高下的面积（S）的图像即可。
说到这，小美兴趣直接来了，于是乎，小美就开始寻找\(S\)与\(h\)的关系。
首先，小美将圆锥的纵向切开，可以想到那是一个三角形：

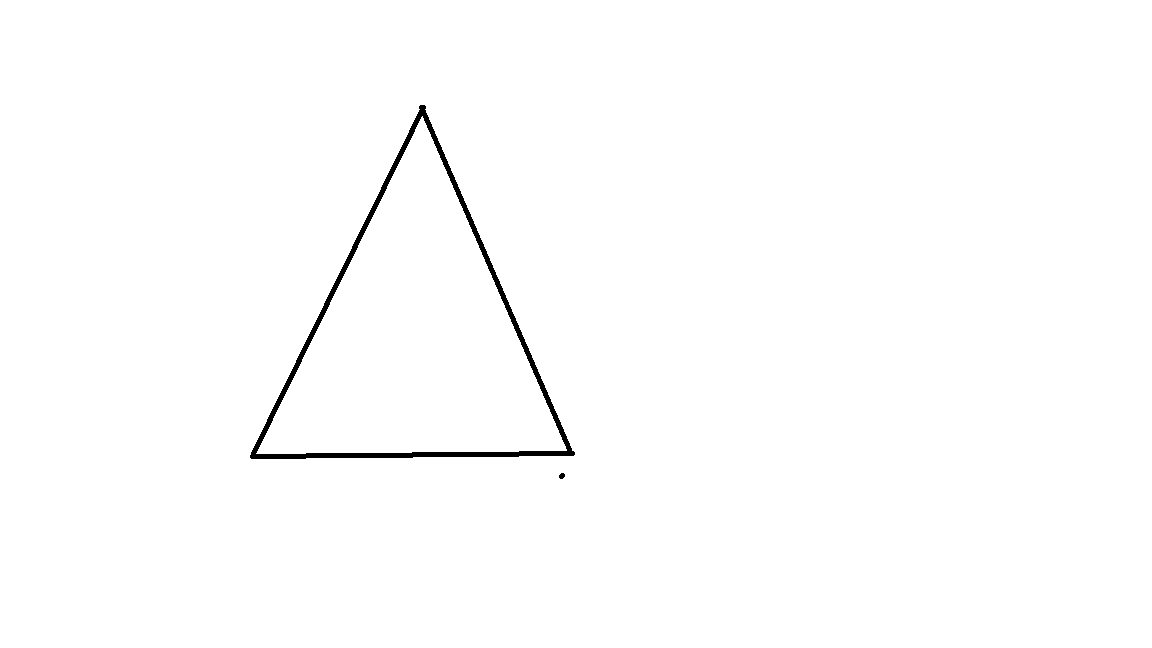
很好，假设这是一个底面圆的面积是\(S_{1}\)，高为\(h_{1}\)的一个圆锥，那么就有：

但是似乎直接用\(S\)来表示有一些抽象，不如换一换：
假设这个圆的半径是\(r\),则有\(S\)=\(\pi\)\(r^{2}\)
那好了，现在这个图就变成了：

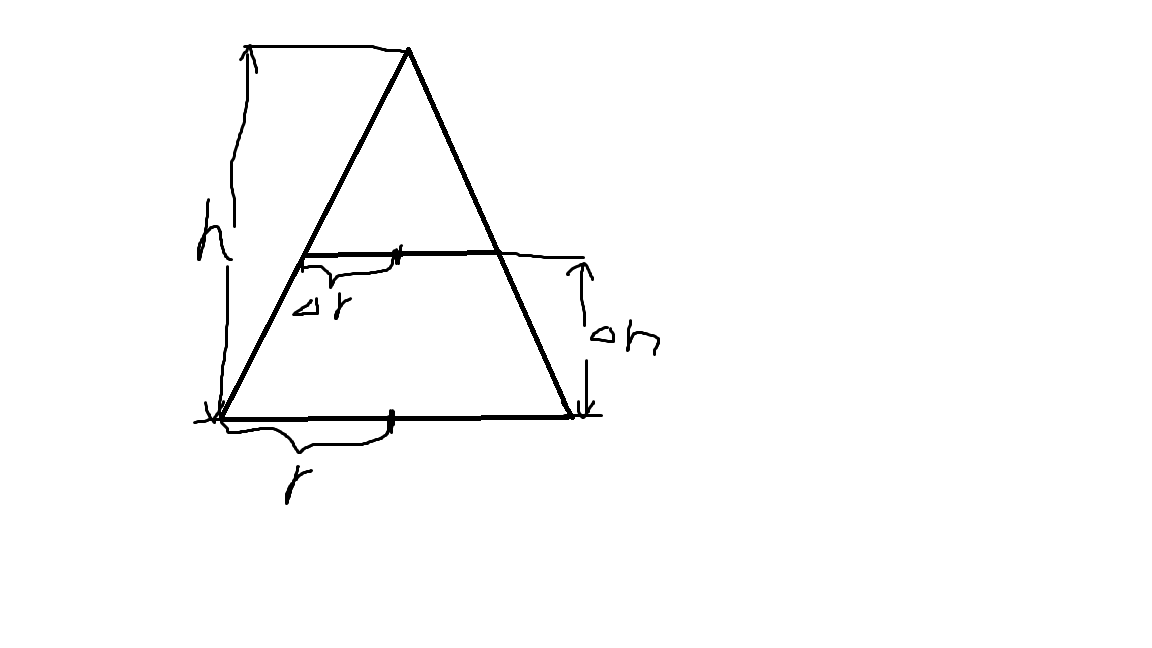
这下可以用相似解决了，小美得到了如下的等式：

\[\frac{h_{1}-\Delta h}{h_{1}}=\frac{\Delta r}{r} \]

整理一下，就是：

\[r h_{1}-r \Delta h =h_{1} \Delta r \]

\[r-\frac{r}{h_{1}} \Delta h=\Delta r \]

又依据\(S\)=\(\pi r^{2}\)，就可以得到\(S\)与\(h\)的关系啦：

\[S=\pi (r-\frac{r}{h_{1}} h)^{2} \]

其中\(r\),\(h_{1}\)都是常量。
小美解决了\(S\)与\(h\)关系的问题,把这个圆锥以及它同高同圆底面积的圆柱画在图像上，就像下面这样👇

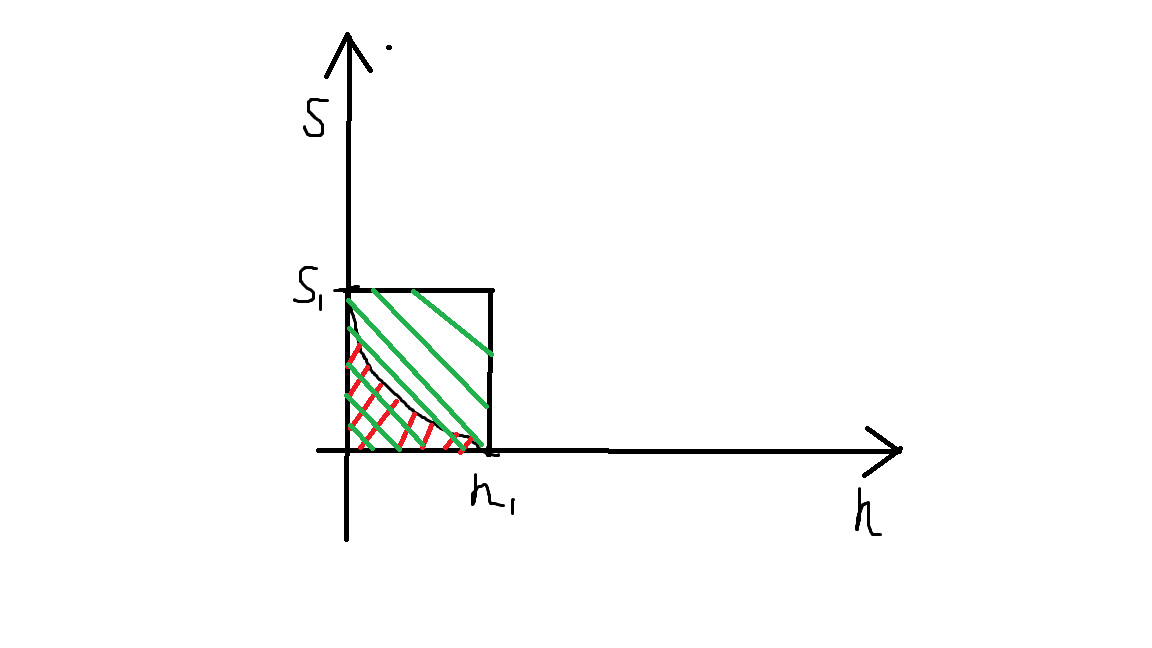
（忽略小美由于没有ggb而画的极其不标准的图像）
这下只要求出红色阴影面积与绿色阴影面积的关系即可。
此时陷入了难题，该怎么求啊？
小美对此引入了一个微积分的基本定理：

\[牛顿莱布尼茨公式 \]

什么是牛顿莱布尼茨公式呢？
内容是这样的：

一个连续函数在区间 [ a，b ] 上的定积分等于它的任意一个原函数在区间[ a，b ]上的增量。

定义是这样的：
如果函数\(f(x)\)在区间\([a,b]\)上连续，且存在原函数\(F(x)\)
则

\[\int_{a}^{b}f(x)dx=F(b)-F(a) \]

那么它可以解决什么？
我们可以利用它计算平面曲线围成的面积。
由于这个太高深了，小美只是想用它解决一个简单的问题，所以小美只用它的简单的推论：
设\(F(x)\)的导函数为\(f(x)\),以\(F(x)\)=\(x^{2}\)为例，那么\(f(x)\)=\(2x\)。
在\(f(x)\)的定义域里任取a,b,如图：

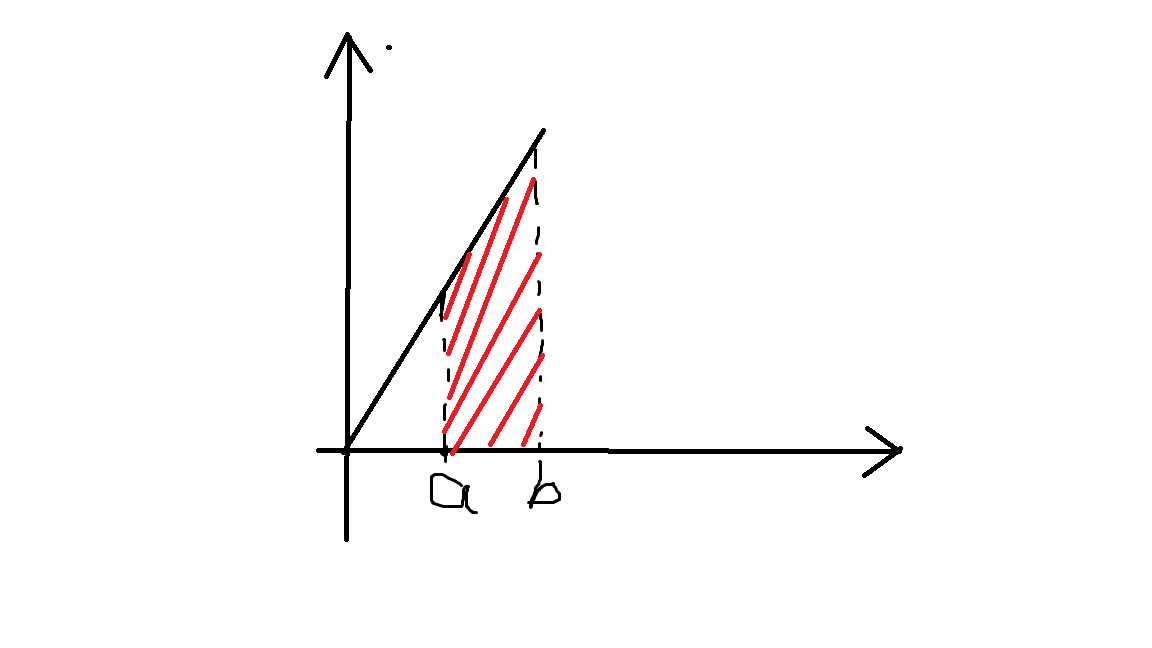
红色阴影部分面积是多少呢？
就是把a,b分别带入\(F(x)\)里，即\(F(b)\)-\(F(a)\)的值就是红色阴影的面积。
那么同样，如果把上面求出来的\(S\)与\(h\)的表达式抽象一下，就是：

\[f(x)=\pi (\frac{r}{h_{1}} x-r)^{2} \]

其中\(x \epsilon[0,h_{1}]\)。
同理，\(f(x)\)是一个\(F(x)\)的导函数，这个\(F(x)\)可以是：

\[F(x)=\frac{\pi}{3} (r-\frac{r}{h_{1}} h)^{3} \]

将\(x=0\)与\(x\)=\(h_{1}\)分别带入，求得其面积为\(\frac{\pi}{3} r^{3}\)。
呃……这似乎只能证明这个圆锥的体积是底面积为\(\pi r^{2}\)，高为\(r\)的圆柱的\(\frac{1}{3}\)，但是别急，小美直接由特殊到一般推广，所以就是开始的结论了。(doge