【小知识酷】《Matlab》考点精简
在线编译器 https://matlab.mathworks.com/?elqsid=umic49viv8wu5r6fckew
第1章 matlab基础知识
第1节 输出函数
1. 使用disp函数
disp函数可用于输出变量的值或者字符串。
% 输出字符串
disp('Hello, MATLAB!'); %显示Hello, MATLAB!
% 输出变量
x = 10;
disp(x); %显示10
% 输出数组元素
A = [10, 20, 30, 40, 50];
disp(A); %显示10 20 30 40 50
2. 使用fprintf函数
fprintf函数能按照指定的格式输出数据,这和C语言里的printf函数类似。
% 输出格式化的字符串和变量
x = 3.14159;
fprintf('The value of x is %.2f\n', x); %保留2位小数,并四舍五入,显示3.14
3. 使用sprintf函数
sprintf函数和fprintf函数类似,不过它是把格式化后的字符串返回,而非直接输出。
% 将格式化后的字符串赋值给变量
x = 2.71858;
str = sprintf('The value of x is %.3f', x);
disp(str); %保留3位小数,并四舍五入,显示2.719
4. 直接在命令窗口输入变量名
在命令窗口直接输入变量名,回车后就能显示变量的值。
y = [1, 2, 3, 4, 5];
y
第2节 input输入函数
在MATLAB中,input函数用于从用户处获取输入,它有多种使用方式,下面为你详细介绍其语法和示例。
基本语法
1. x = input(prompt)
这种语法会在命令窗口显示prompt提示信息,然后等待用户输入内容,最后将用户输入的内容作为结果返回给变量x。如果用户输入的是有效的MATLAB表达式,MATLAB会计算该表达式的值并返回;如果输入的是字符串,需要用单引号将其括起来。
x = input('请输入一个数字: ');
disp(['你输入的数字是: ', num2str(x)]);
在这个示例里,运行代码后命令窗口会显示请输入一个数字: ,等待用户输入。若用户输入5,程序会把这个数字赋值给变量x,并在后续显示出你输入的数字是: 5。
2. x = input(prompt,'s')
在这种形式中,'s'参数表明将用户输入的内容按字符串形式处理,无论用户输入什么,都会直接作为字符串返回给变量x,而不会对其进行表达式计算。
name = input('请输入你的名字: ','s');
disp(['你输入的名字是: ', name]);
运行此代码,命令窗口会显示请输入你的名字: ,当用户输入张三时,程序会把张三作为字符串赋值给变量name,并显示你输入的名字是: 张三。
输入验证和错误处理
在实际使用中,为保证输入的有效性,可能需要对用户输入进行验证和错误处理。以下是一个简单的示例,确保用户输入的是正数:
while true
num = input('请输入一个正数: ');
if num > 0
disp(['你输入的正数是: ', num2str(num)]);
break;
else
disp('输入无效,请输入一个正数。');
end
end
这个代码会持续提示用户输入正数,若用户输入的不是正数,会显示错误提示并要求重新输入,直到输入有效的正数为止。
综上所述,input函数是MATLAB中获取用户输入的重要工具,可根据具体需求选择合适的语法形式。
第3节 算术运算
在MATLAB里,*与.*、/与./是用途不同的运算符,下面为你详细讲解它们的区别以及MATLAB里的其他常见运算符。
*和.*的区别
*(矩阵乘法运算符):用于执行矩阵乘法,需遵循矩阵乘法规则,即第一个矩阵的列数要和第二个矩阵的行数相等。.*(点乘运算符):用于数组对应元素相乘,要求参与运算的两个数组大小相同,会把两个数组对应位置的元素相乘。
以下是示例代码:
% 定义矩阵 A 和 B
A = [1, 2; 3, 4];
B = [5, 6; 7, 8];
% 矩阵乘法
C = A * B;
disp('矩阵乘法 A * B 的结果:');
disp(C);
% 数组点乘
D = A .* B;
disp('数组点乘 A .* B 的结果:');
disp(D);
输出结果:
矩阵乘法 A * B 的结果:
19 22
43 50
数组点乘 A .* B 的结果:
5 12
21 32
计算过程:
A | B
1 2 | 5 6
3 4 | 7 8
A * B的结果:
1×5+2×7=19 1×6+2×8=22
3×5+4×7=43 3×6+4×8=50
A .* B的结果:
1×5=5 2×6=12
3×7=21 4×8=32
/和./的区别
/(矩阵右除运算符):用于求解线性方程组X * B = A的解X,相当于X = A / B = A * inv(B),不过MATLAB会采用更高效的算法避免直接求逆。./(点除运算符):用于数组对应元素相除,要求参与运算的两个数组大小相同,会用第一个数组的每个元素除以第二个数组对应位置的元素。
以下是示例代码:
% 定义矩阵 A 和 B
A = [1, 2; 3, 4];
B = [5, 6; 7, 8];
% 矩阵右除
C = A / B;
disp('矩阵右除 A / B 的结果:');
disp(C);
% 数组点除
D = A ./ B;
disp('数组点除 A ./ B 的结果:');
disp(D);
输出结果:
矩阵右除 A / B 的结果:
-3.0000 -2.0000
4.0000 3.0000
数组点除 A ./ B 的结果:
0.2000 0.3333
0.4286 0.5000
MATLAB中的其他常见运算符
算术运算符
+:用于标量、数组和矩阵的加法运算。-:用于标量、数组和矩阵的减法运算。^:矩阵幂运算,用于计算矩阵的幂。.^:点幂运算符,用于计算数组每个元素的幂。
关系运算符
==:判断是否相等,返回逻辑数组。~=:判断是否不相等,返回逻辑数组。>:判断是否大于,返回逻辑数组。<:判断是否小于,返回逻辑数组。>=:判断是否大于等于,返回逻辑数组。<=:判断是否小于等于,返回逻辑数组。
逻辑运算符
&:逻辑与运算,对两个逻辑数组或标量逐元素进行逻辑与操作。|:逻辑或运算,对两个逻辑数组或标量逐元素进行逻辑或操作。~:逻辑非运算,对逻辑数组或标量逐元素进行逻辑非操作。&&:短路逻辑与,用于标量逻辑与运算,若第一个操作数为false,则不计算第二个操作数。||:短路逻辑或,用于标量逻辑或运算,若第一个操作数为true,则不计算第二个操作数。
其他运算符
::冒号运算符,用于创建向量、指定索引范围等。':矩阵转置运算符,用于求矩阵的转置。.:结构体成员访问运算符,用于访问结构体的成员。
第4节 变量名
在MATLAB中,合法的变量名需要遵循一定的规则,以下为你详细介绍这些规则以及示例:
变量名命名规则
- 以字母开头:变量名的第一个字符必须是字母,不能是数字、特殊字符等。
- 后续字符限制:变量名可以包含字母、数字和下划线
_,但不能包含空格、标点符号等其他特殊字符。 - 区分大小写:MATLAB是区分大小写的,所以
myVariable和myvariable被视为两个不同的变量。 - 长度限制:虽然MATLAB对变量名的长度没有严格的硬性规定,但为了代码的可读性和兼容性,建议变量名不要过长。
- 避免使用关键字:不能使用MATLAB的关键字(如
if、else、for、while等)作为变量名,否则会导致语法错误。你可以使用iskeyword函数查看MATLAB的所有关键字。
合法与不合法变量名示例
合法变量名
myVariable:以字母开头,后续包含字母,符合命名规则。var_1:以字母开头,包含字母和下划线,是合法的变量名。AnotherVar:同样以字母开头,后续包含字母,区分大小写,也是合法的。
不合法变量名
123var:以数字开头,不符合变量名必须以字母开头的规则。my-var:包含连字符-,变量名只能包含字母、数字和下划线。if:这是MATLAB的关键字,不能作为变量名使用。
第5节 char 和 string
在MATLAB中,char 和 string 都用于处理文本数据,但它们在存储方式、操作方法和适用场景等方面存在明显区别,下面为你详细介绍:
1. 存储方式
char(字符数组):char类型以字符数组的形式存储文本,它是一个二维的 ASCII 字符矩阵,每一行代表一个字符串。当存储多个字符串时,如果字符串长度不一致,MATLAB 会用空格填充较短的字符串,使它们长度相同。
char_array = ['Hello'; 'World'];
disp(char_array);
在上述代码中,由于 'Hello' 和 'World' 长度相同,它们可以正常存储在一个 char 数组中。若长度不同,短的字符串会被空格填充。
string(字符串数组):string类型是在 MATLAB R2016b 及以后版本引入的,它以字符串数组的形式存储文本,每个元素可以是不同长度的字符串,不需要用空格填充。
string_array = ["Hello", "World"];
disp(string_array);
这里 string_array 中的每个元素都是一个独立的字符串,长度可以不同。
2. 输入与创建方式
char:可以使用单引号创建字符数组,也可以使用char函数将其他数据类型转换为字符数组。
% 使用单引号创建
char1 = 'Hello';
% 使用 char 函数转换
num = 123;
char2 = char(num);
string:使用双引号创建字符串数组,也可以使用string函数进行转换。
% 使用双引号创建
string1 = "Hello";
% 使用 string 函数转换
str = string(num);
3. 操作方法
- 索引与访问
char:通过行和列索引访问字符数组中的元素。
char_array = ['Hello'; 'World'];
char_element = char_array(1, 2); % 访问第一行第二列的字符 'e'
string:使用线性索引访问字符串数组中的元素。
string_array = ["Hello", "World"];
string_element = string_array(2); % 访问第二个字符串 'World'
- 拼接操作
char:使用方括号[]进行拼接,需要注意字符串长度匹配问题。
char1 = 'Hello';
char2 = 'World';
combined_char = [char1, ' ', char2];
string:使用加号+或字符串拼接函数strcat进行拼接,操作更方便。
string1 = "Hello";
string2 = "World";
combined_string = string1 + " " + string2;
- 字符串函数的使用:许多字符串处理函数对
char和string的处理方式略有不同。例如,strlength函数用于计算字符串的长度,对于char数组,它会返回每一行的字符数;对于string数组,它会返回每个元素的字符数。
char_array = ['Hello'; 'World'];
string_array = ["Hello", "World"];
char_lengths = strlength(char_array);
string_lengths = strlength(string_array);
4. 适用场景
char:在需要与旧代码兼容,或者处理固定长度字符串的场景中使用较多,例如处理文本文件中的格式化数据。string:在现代 MATLAB 编程中,处理动态长度字符串和字符串数组时更为方便,适用于字符串的拼接、比较、查找等操作。
综上所述,char 和 string 各有特点,你可以根据具体的需求选择合适的数据类型来处理文本数据。
第6节 常用函数
fix、power、abs
第2章 matlab程序设计
第1节 if判断语句
在MATLAB里,if语句用于依据条件判断来决定是否执行特定的代码块。它有多种形式,下面为你详细介绍。
1. 基本的if语句
这种形式只有一个条件判断,当条件为真时,执行对应的代码块。
x = 10;
if x > 5
disp('x 大于 5');
end
在这个例子里,由于x的值是10,大于5,所以条件为真,会执行disp('x 大于 5');语句。
2. if - else语句
当条件为真时,执行if后面的代码块;当条件为假时,执行else后面的代码块。
x = 3;
if x > 5
disp('x 大于 5');
else
disp('x 小于或等于 5');
end
这里x的值是3,不大于5,条件为假,因此会执行disp('x 小于或等于 5');语句。
3. if - elseif - else语句
可以使用elseif来添加更多的条件判断,当if的条件为假时,会依次判断elseif的条件,若都不满足,则执行else后面的代码块。
x = 0;
if x > 0
disp('x 是正数');
elseif x < 0
disp('x 是负数');
else
disp('x 是零');
end
此例中x的值为0,不满足x > 0和x < 0的条件,所以会执行disp('x 是零');语句。
4. 嵌套if语句
在if语句的代码块中还可以再嵌套if语句,以实现更复杂的条件判断。
x = 10;
y = 5;
if x > 5
if y > 3
disp('x 大于 5 且 y 大于 3');
end
end
在这个嵌套if语句里,首先判断x > 5,条件为真,接着进入内层if语句,判断y > 3,条件也为真,所以会执行disp('x 大于 5 且 y 大于 3');语句。
总结来说,if语句在MATLAB里是非常实用的条件控制结构,能依据不同的条件来执行不同的代码逻辑。
【例题】计算分段函数P46
x=input('请输入一个数:');
if x<0
y=abs(x);
elseif x<10
y=sin(x)./(x+1);
elseif x<20
y=pow(x,3);
else
y=(3+2*x).*log(x);
end
disp(y);
第3节 不同类型的比较操作
在MATLAB中,==、~=、> 、< 、>= 、<= 分别用于不同类型的比较操作,下面为你详细介绍它们的语法和使用示例:
1. ==(相等比较)
== 用于比较两个值或数组的对应元素是否相等,返回一个逻辑数组(若输入为数组)或一个逻辑标量(若输入为标量),相等的位置为 true(即 1),不相等的位置为 false(即 0)。
% 标量比较
a = 5;
b = 5;
result1 = a == b;
disp(result1);
% 数组比较
A = [1, 2, 3];
B = [1, 4, 3];
result2 = A == B;
disp(result2);
2. ~=(不等于比较)
~= 用于比较两个值或数组的对应元素是否不相等,同样返回一个逻辑数组或逻辑标量,不相等的位置为 true,相等的位置为 false。
% 标量比较
a = 5;
b = 6;
result3 = a ~= b;
disp(result3);
% 数组比较
A = [1, 2, 3];
B = [1, 4, 3];
result4 = A ~= B;
disp(result4);
3. >=(大于等于比较)
>= 用于比较两个值或数组的对应元素,判断左边的元素是否大于或等于右边的元素,返回的逻辑数组或逻辑标量中,满足条件的位置为 true,不满足条件的位置为 false。
% 标量比较
a = 5;
b = 3;
result5 = a >= b;
disp(result5);
% 数组比较
A = [1, 2, 3];
B = [1, 4, 3];
result6 = A >= B;
disp(result6);
这些比较运算符在MATLAB的条件判断、数组筛选等操作中非常常用。例如,可以使用它们结合 if 语句来实现条件控制,或者结合逻辑索引来筛选数组中的元素。
第4节 switch语句
在MATLAB中,switch语句是一种条件控制结构,用于根据表达式的值来选择执行不同的代码块,它可以替代多个嵌套的if-elseif-else语句,使代码更加简洁易读。以下是switch语句的详细语法和使用示例。
基本语法
switch expression
case value1
% 当 expression 的值等于 value1 时执行的代码
statements1
case value2
% 当 expression 的值等于 value2 时执行的代码
statements2
...
case valueN
% 当 expression 的值等于 valueN 时执行的代码
statementsN
otherwise
% 当 expression 的值不等于任何一个 case 值时执行的代码
statements_otherwise
end
expression:是一个表达式,其值将与各个case后面的值进行比较。case value:value可以是标量、向量或字符串,当expression的值与某个case后面的值相等时,就会执行该case下的代码块。otherwise:是可选的,当expression的值不等于任何一个case后面的值时,会执行otherwise下的代码块。
使用示例
示例1:根据数字选择执行不同的操作
x = 2;
switch x
case 1
disp('x 的值是 1');
case 2
disp('x 的值是 2');
case 3
disp('x 的值是 3');
otherwise
disp('x 的值不是 1、2 或 3');
end
在这个例子中,x的值为2,所以会执行case 2下的代码块,输出x 的值是 2。
示例2:使用向量作为case值
x = [1, 2];
y = [1, 2];
switch isequal(x, y)
case true
disp('x 和 y 相等');
case false
disp('x 和 y 不相等');
end
这里使用isequal函数比较x和y是否相等,返回一个布尔值。根据这个布尔值,选择执行相应的代码块。
示例3:处理多个值匹配的情况
x = 3;
switch x
case {1, 2}
disp('x 的值是 1 或 2');
case {3, 4}
disp('x 的值是 3 或 4');
otherwise
disp('x 的值不是 1、2、3 或 4');
end
在这个例子中,x的值为3,所以会执行case {3, 4}下的代码块,输出x 的值是 3 或 4。
注意事项
switch语句中的比较是严格相等的比较,即值和类型都要相同。- 一旦某个
case条件满足,执行完该case下的代码块后,会跳出switch语句,不会继续检查后面的case条件。 otherwise分支可以省略,如果省略且没有匹配的case条件,则不会执行任何代码。
第5节 for函数的使用
在MATLAB里,for循环是用来重复执行特定代码块的控制结构,可按照指定的次数或者遍历数组元素来执行操作。下面详细介绍for循环的常见使用方式。
1. 基于数值范围的for循环
借助冒号运算符来指定循环变量的取值范围,格式为for 循环变量 = 起始值:步长:终止值,若不指定步长,默认步长为1。
% 步长为1的情况
for i = 1:5
fprintf('%d ',i);
end
fprintf("\n") %换行
% 指定步长为2的情况
for j = 1:2:10
fprintf("%d ",j);
end
%输出如下:
1 2 3 4 5
1 3 5 7 9
在第一个例子中,循环变量i从1开始,每次增加1,直到达到5,循环体中使用disp函数输出i的值。
第二个例子里,循环变量j从1开始,步长为2,直到达到10。
2. 使用end关键字结束循环
在MATLAB里,for循环必须以end关键字结尾,以此来标识循环体的结束。若缺少end,会导致语法错误。
总结而言,for循环在MATLAB中是一种很有用的控制结构,能够根据需求实现不同的循环逻辑。
3. 遍历数组元素的for循环
for循环能直接遍历数组的每个元素。
A = [10, 20, 30, 40, 50];
for element = A
disp(element);
end
这里的A是一个数组,循环变量element会依次取数组A中的每个元素,并将其输出。
4. 嵌套for循环
可以在一个for循环内部嵌套另一个for循环,用于处理二维数组或者实现更复杂的逻辑。
for i = 1:3
for j = 1:2
result = i * j;
fprintf('i = %d, j = %d, i * j = %d\n', i, j, result);
end
end
在这个嵌套for循环中,外层循环控制i的值从1到3,内层循环控制j的值从1到2,每次循环都会计算i和j的乘积并输出。
【例题1】对于三位数而言,若一个三位数的百位、十位、个位数字的立方和等于该数本身,那它就是水仙花数。输出100~999之间的水仙花数
num=[];
for i=100:999
g=mod(i,10);
s=mod(fix(i/10),10);
b=fix(i/100);
sum = power(g,3)+power(s,3)+power(b,3);
if sum==i
num = [num,sum]; %存入结果
end
end
disp(num); %输出153 370 371 407
【例题2】若一个数等于它的各个真因子之和,则称该数为完数,如6=1+2+3,所以6是完数。求[1,100]之间的全部完数。
for num=1:100 %1~100之间
s=0;
for i=1:num
if num%i==0
s = s + i; %将因子数相加
if num==s
fprintf('%d ',s);
end
end
end
end
第6节 break和continue
在MATLAB中,break和continue都是用于控制循环流程的关键字,它们在循环结构(如for循环和while循环)中发挥着不同的作用,下面为你详细介绍二者的区别。
1. break语句
break语句的主要作用是立即终止当前所在的循环,无论循环条件是否满足,程序都会跳出该循环,继续执行循环之后的代码。
示例代码
for i = 1:10
if i == 5
break;
end
disp(i);
end
disp('循环已终止');
代码解释
在这个for循环中,当变量i的值等于5时,break语句会被执行,循环会立即终止,不再执行后续的循环迭代。所以,代码只会输出1到4的数字,然后输出循环已终止。
2. continue语句
continue语句用于跳过当前循环迭代中continue语句之后的代码,直接进入下一次循环迭代。也就是说,它会忽略本次循环剩余的代码,但是循环会继续执行,直到循环条件不再满足。
示例代码
for i = 1:10
if i == 5
continue;
end
disp(i);
end
disp('循环已结束');
代码解释
在这个for循环中,当变量i的值等于5时,continue语句会被执行,disp(i);语句会被跳过,直接进入下一次循环迭代。所以,代码会输出除5之外的1到10的数字,最后输出循环已结束。
总结
break:终止整个循环,跳出循环体,不再执行后续的循环迭代。continue:跳过当前循环迭代中continue语句之后的代码,直接进入下一次循环迭代,循环会继续执行。
在实际编程中,你可以根据具体的需求选择使用break或continue来控制循环的执行流程。
章节练习
第4章 图形绘制
在MATLAB里,可借助多种函数来绘制不同类型的图形,下面为你详细介绍常见图形绘制的语法和示例。
1. 二维折线图(plot函数)
plot函数是MATLAB中用于绘制二维折线图的常用函数,其基本语法如下:
plot(x, y)
- 参数说明:
x:是一个包含 \(x\) 坐标值的向量。y:是一个包含 \(y\) 坐标值的向量,且x和y的长度必须相同。
示例
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y);
此示例绘制了正弦函数 \(y = \sin(x)\) 在区间 \([0, 2\pi]\) 上的曲线。
2. 多个数据集的折线图
可以在同一个图形窗口中绘制多个数据集的折线图,语法如下:
plot(x1, y1, x2, y2, ...)
- 参数说明:
x1, y1:是第一组 \(x\) 和 \(y\) 坐标值的向量。x2, y2:是第二组 \(x\) 和 \(y\) 坐标值的向量,以此类推。
示例
x = 0:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, x, y2);
该示例在同一个图形窗口中绘制了正弦函数和余弦函数的曲线。
3. 散点图(scatter函数)
scatter函数用于绘制散点图,其基本语法如下:
scatter(x, y)
- 参数说明:
x:是一个包含 \(x\) 坐标值的向量。y:是一个包含 \(y\) 坐标值的向量,且x和y的长度必须相同。
示例
x = rand(1, 100);
y = rand(1, 100);
scatter(x, y);
此示例绘制了 100 个随机点的散点图。
4. 柱状图(bar函数)
bar函数用于绘制柱状图,其基本语法如下:
bar(x, y)
- 参数说明:
x:是一个包含柱子位置的向量(可选)。y:是一个包含柱子高度的向量。
示例
y = [1, 3, 2, 4, 5];
bar(y);
该示例绘制了一个简单的柱状图。
5. 饼图(pie函数)
pie函数用于绘制饼图,其基本语法如下:
pie(x)
- 参数说明:
x:是一个包含各部分数值的向量。
示例
x = [10, 20, 30, 40];
pie(x);
此示例绘制了一个饼图,展示各部分的比例关系。
6. 图形属性设置
可以通过设置图形的属性来改变图形的外观,例如线条颜色、标记样式等。以下是一个示例:
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, 'r--o');
在这个示例中,'r--o' 是一个属性字符串,'r' 表示线条颜色为红色,'--' 表示线条样式为虚线,'o' 表示标记样式为圆形。
7. 添加标题、标签和图例
可以使用以下函数为图形添加标题、坐标轴标签和图例:
x = 0:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, 'r', x, y2, 'b');
title('正弦和余弦函数曲线');
xlabel('x');
ylabel('y');
legend('正弦函数', '余弦函数');
此示例为图形添加了标题、坐标轴标签和图例,使图形更加清晰易懂。
在MATLAB中,绘制图形时可以通过设置曲线样式、线型、颜色和数据点标记等选项来改变图形的外观,使图形更加清晰和美观。下面为你详细介绍这些选项及其使用方法。
1. 曲线样式的综合设置
在 plot 函数中,可以通过一个字符串来同时设置颜色、线型和数据点标记。其基本语法如下:
plot(x, y, '选项字符串')
例如:
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, 'r--o');
这里的 'r--o' 就是一个选项字符串,其中 'r' 表示颜色为红色,'--' 表示线型为虚线,'o' 表示数据点标记为圆形。
2. 线型选项
线型用于定义曲线的外观形状,常见的线型选项如下:
| 线型符号 | 描述 |
|---|---|
- |
实线(默认值) |
-- |
虚线 |
: |
点线 |
-. |
点划线 |
示例代码:
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, '--'); % 绘制虚线曲线
3. 颜色选项
颜色选项用于指定曲线或数据点的颜色,常见的颜色选项如下:
| 颜色符号 | 描述 | 颜色符号 | 描述 |
|---|---|---|---|
'r' |
红色 | 'g' |
绿色 |
'b' |
蓝色 | 'c' |
青色 |
'm' |
品红色 | 'y' |
黄色 |
'k' |
黑色 | 'w' |
白色 |
示例代码:
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, 'g'); % 绘制绿色曲线
4. 数据点标记选项
数据点标记选项用于在曲线上标记数据点的形状,常见的数据点标记选项如下:
| 标记符号 | 描述 | 标记符号 | 描述 |
|---|---|---|---|
'.' |
点 | 'o' |
圆圈 |
'x' |
叉号 | '+' |
加号 |
'*' |
星号 | 'd' |
菱形 |
'^' |
上三角 | 'v' |
下三角 |
'>' |
右三角 | '<' |
左三角 |
示例代码:
x = 0:0.1:2*pi;
y = sin(x);
plot(x, y, 'o'); % 绘制带有圆圈标记的数据点曲线
5. 综合示例
下面的示例展示了如何同时使用不同的线型、颜色和数据点标记绘制多条曲线:
x = 0:0.1:2*pi;
y1 = sin(x);
y2 = cos(x);
% 绘制正弦曲线,红色实线,圆形标记
plot(x, y1, 'r-o');
hold on; % 保持当前图形窗口,以便继续绘制
% 绘制余弦曲线,蓝色虚线,正方形标记
plot(x, y2, 'b--s');
hold off; % 关闭保持状态
title('正弦和余弦函数曲线');
xlabel('x');
ylabel('y');
legend('正弦函数', '余弦函数');
在这个示例中,首先绘制了正弦函数曲线,使用红色实线和圆形标记;然后使用 hold on 命令保持当前图形窗口,接着绘制了余弦函数曲线,使用蓝色虚线和正方形标记;最后添加了标题、坐标轴标签和图例。
通过合理选择线型、颜色和数据点标记,可以使图形更加清晰、直观,便于分析和展示数据。
第5章 线性代数中的计算
第1节 特殊矩阵
在MATLAB中,特殊矩阵是具有特定结构或性质的矩阵,在数学计算、工程建模等诸多领域应用广泛。以下是一些常见特殊矩阵及其生成语法和特性:
1. 零矩阵
- 功能:元素全为0的矩阵,常用于初始化矩阵,在构建复杂矩阵运算结构或表示无信号等场景使用。
- 语法:
zeros(m,n)生成 \(m\) 行 \(n\) 列的零矩阵;zeros(n)生成 \(n\) 阶方阵(行数和列数都为 \(n\) );zeros(size(A))生成与矩阵A大小相同的零矩阵。 - 示例:
A = zeros(3,4); % 生成3行4列的零矩阵
B = zeros(5); % 生成5阶零方阵
2. 单位矩阵
- 功能:主对角线元素全为1,其余元素全为0的方阵。在矩阵运算中,如同乘法运算里的数字1,任何矩阵乘以单位矩阵都等于其本身,常用于矩阵求逆等运算的初始设置等。
- 语法:
eye(n)生成 \(n\) 阶单位矩阵;eye(m,n)生成 \(m\) 行 \(n\) 列的单位矩阵(非方阵情况,主对角线元素为1 )。 - 示例:
C = eye(4); % 生成4阶单位矩阵
D = eye(3,5); % 生成3行5列的单位矩阵
3. 全1矩阵
- 功能:元素全为1的矩阵,可用于快速构建相同权重的矩阵结构,在一些加权计算、初始化矩阵用于特定迭代计算等场景有应用。
- 语法:
ones(m,n)生成 \(m\) 行 \(n\) 列的全1矩阵;ones(n)生成 \(n\) 阶全1方阵;ones(size(A))生成与矩阵A大小相同的全1矩阵。 - 示例:
E = ones(2,3); % 生成2行3列的全1矩阵
F = ones(4); % 生成4阶全1方阵
4. 对角矩阵
- 功能:除主对角线元素外其余元素都为0的矩阵。用于表示具有独立特征的线性变换等场景,在特征值、特征向量相关计算以及数据的解耦处理中有重要应用。
- 语法:
diag(v)以向量v为主对角线元素生成对角矩阵;diag(A)提取矩阵A的主对角线元素构成向量。 - 示例:
v = [1, 2, 3];
G = diag(v); % 以向量v生成对角矩阵
H = [1, 2, 3; 4, 5, 6; 7, 8, 9];
diag_elements = diag(H); % 提取矩阵H的主对角线元素
5. 希尔伯特矩阵
- 功能:元素值为 \(H_{i,j}=\frac{1}{i + j - 1}\) 的矩阵,是典型的病态矩阵(条件数很大,矩阵稍有扰动,其解就会有很大变化 ),常用于数值分析中测试算法的稳定性。
- 语法:
hilb(n)生成 \(n\) 阶希尔伯特矩阵。 - 示例:
I = hilb(3); % 生成3阶希尔伯特矩阵
6. 范德蒙矩阵
- 功能:由向量
v生成的矩阵,其第 \(i\) 行第 \(j\) 列元素为 \(v(i)^{(n - j)}\)(\(n\) 为矩阵阶数 ),在数值分析、多项式插值等领域有应用。 - 语法:
vander(v)以向量v生成范德蒙矩阵。 - 示例:
v = [1, 2, 3];
J = vander(v); % 以向量v生成范德蒙矩阵
第2节 数组(矩阵)
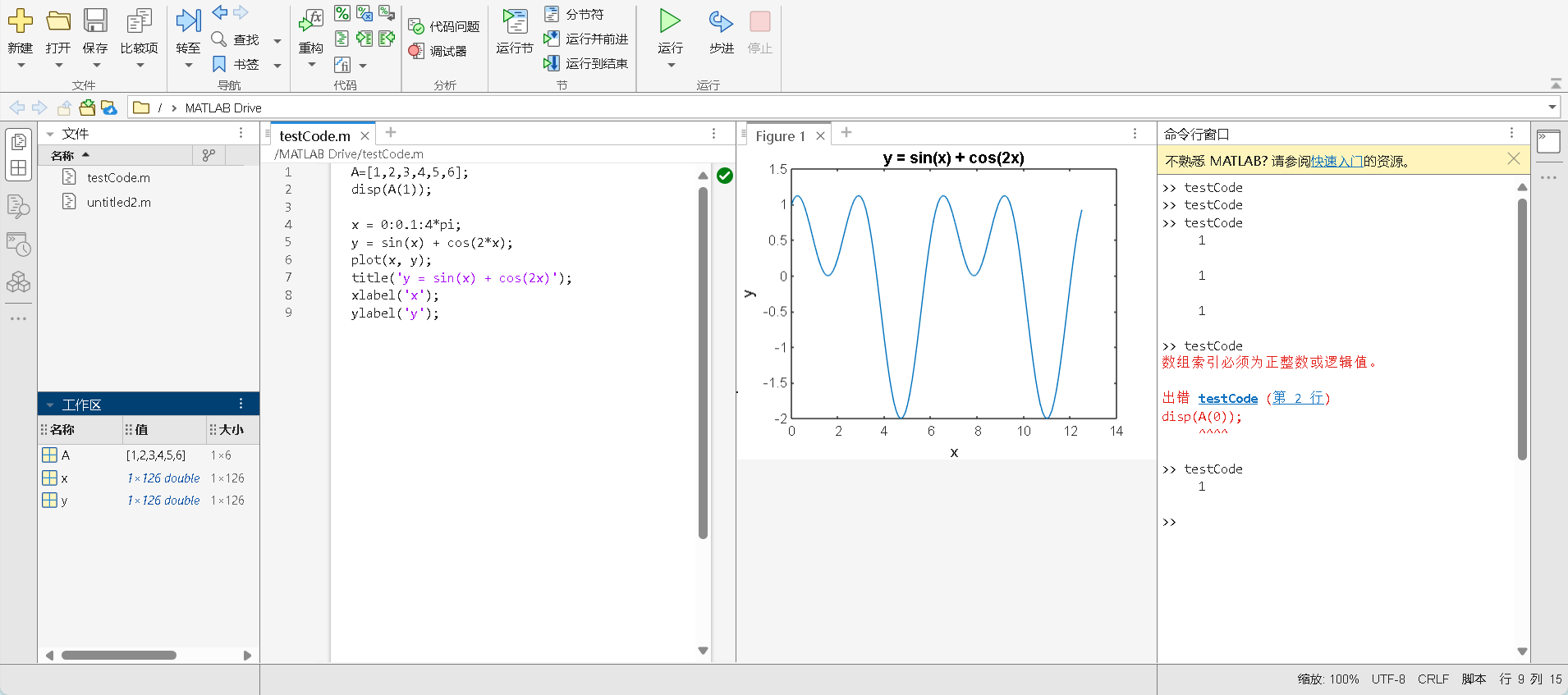
在MATLAB中,数组(矩阵)的索引是按列优先进行的 。对于矩阵A=[1,2,3;4,5,6] ,它是一个2行3列的矩阵,元素的存储顺序是先按行存储。
索引从1开始计数,按列读取。A(a)表示取矩阵A的第a个元素;A(a,b)其中a是行索引,b是列索引。
所以A(3)的值是2,A(4)是6,A(2,3)表示第2行第3列的值是7。
A=[1,2,3,4; 5,6,7,8];
disp(A);
fprintf("A(3):%d,A(4):%d\n",A(3),A(4));
fprintf("A(2,3):%d\n",A(2,3));
%输出内容:
1 2 3 4
5 6 7 8
A(3):2,A(4):6
A(2,3):7
第3节 升序和降序
在MATLAB里,对数组进行升序和降序排序是很常见的操作,下面为你详细介绍实现升序和降序排序的方法。
1. 升序排序
在MATLAB中,使用sort函数能够实现数组的升序排序,这是默认的排序方式。
语法
B = sort(A)
A是输入的数组,可以是向量或者矩阵。B是排序后的数组。
示例
% 对向量进行升序排序
A = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5];
B = sort(A);
disp('升序排序后的向量:');
disp(B);
% 对矩阵的每一列进行升序排序
C = [3, 1; 4, 2; 1, 5];
D = sort(C);
disp('升序排序后的矩阵:');
disp(D);
解释
- 对于向量,
sort函数会将元素按照从小到大的顺序排列。 - 对于矩阵,
sort函数默认按列进行排序,也就是对矩阵的每一列元素分别进行升序排序。
2. 降序排序
同样可以使用sort函数来实现数组的降序排序,只需指定'descend'参数即可。
语法
B = sort(A, 'descend')
A是输入的数组,可以是向量或者矩阵。B是降序排序后的数组。
示例
% 对向量进行降序排序
A = [3, 1, 4, 1, 5];
B = sort(A, 'descend');
disp('降序排序后的向量B:');
disp(B);
% 对矩阵的每一列进行降序排序
C = [3, 1; 4, 2; 1, 5];
D = sort(C, 'descend');
disp('未排序的矩阵C:');
disp(C);
disp('降序排序后的矩阵D:');
disp(D);
>> 控制台输出
降序排序后的向量B:
5 4 3 1 1
未排序的矩阵C:
3 1
4 2
1 5
降序排序后的矩阵D:
4 5
3 2
1 1
解释
- 对于向量,
sort函数会将元素按照从大到小的顺序排列。 - 对于矩阵,
sort函数默认按列进行降序排序,即对矩阵的每一列元素分别进行降序排列。
3. 对矩阵行进行排序
若要对矩阵的行进行升序或降序排序,可以通过指定第二个参数来实现。
升序排序矩阵行
C = [3, 1; 4, 2; 1, 5];
D = sort(C, 2); % 对矩阵的行进行升序排序
disp('按行升序排序后的矩阵:');
disp(D);
降序排序矩阵行
C = [3, 1; 4, 2; 1, 5];
D = sort(C, 2, 'descend'); % 对矩阵的行进行降序排序
disp('按行降序排序后的矩阵:');
disp(D);
总结 【5★】
- 使用
sort(A)可以对数组A进行升序排序。 - 使用
sort(A, 'descend')可以对数组A进行降序排序。 - 对于矩阵,默认按列排序,通过指定第二个参数
2可以按行排序。
第4节 常用函数
在MATLAB中,inv、det、linsolve 和 eig 是四个功能不同的函数,下面为你详细介绍它们的区别。
1. inv 函数
- 功能:
inv函数用于计算矩阵的逆矩阵。对于一个 \(n\) 阶方阵 \(A\),如果存在一个 \(n\) 阶方阵 \(B\),使得 \(AB = BA = I\)(\(I\) 为 \(n\) 阶单位矩阵),则称 \(B\) 是 \(A\) 的逆矩阵,记作 \(A^{-1}\)。只有方阵(行数和列数相等)且行列式不为零(即矩阵可逆)时,才能使用inv函数计算其逆矩阵。 - 语法:
B = inv(A),其中A是输入的方阵,B是计算得到的逆矩阵。 - 示例:
A = [1, 2; 3, 4];
B = inv(A);
disp(B);
- 应用场景:在求解线性方程组 \(Ax = b\)(\(A\) 可逆)时,可以通过 \(x = A^{-1}b\) 来求解 \(x\)。不过在实际应用中,由于直接求逆矩阵的计算量较大且可能存在数值稳定性问题,通常更推荐使用
linsolve函数。
2. det 函数
- 功能:
det函数用于计算矩阵的行列式。行列式是一个与方阵相关的标量值,它可以用来判断矩阵是否可逆(方阵可逆的充要条件是其行列式不为零),还在求解线性方程组、计算矩阵的特征值等方面有重要应用。 - 语法:
d = det(A),其中A是输入的方阵,d是计算得到的行列式的值。 - 示例:
A = [1, 2; 3, 4];
d = det(A);
disp(d);
- 应用场景:判断矩阵是否可逆,在矩阵理论和线性代数的许多计算中作为一个重要的判断依据。
3. linsolve 函数
- 功能:
linsolve函数用于求解线性方程组\(Ax = b\),其中 \(A\) 是系数矩阵,\(x\) 是未知数向量,\(b\) 是常数向量。该函数通过高效的数值算法来求解线性方程组,而不是直接求矩阵的逆,因此在计算效率和数值稳定性上通常优于使用逆矩阵求解。 - 语法:
x = linsolve(A, b),其中A是系数矩阵,b是常数向量,x是求解得到的未知数向量。 - 示例:
A = [1, 2; 3, 4];
b = [5; 6];
x = linsolve(A, b);
disp(x);
- 应用场景:在工程、科学计算等领域中,求解线性方程组是一个常见的问题,
linsolve函数是解决这类问题的常用工具。
4. eig 函数
- 功能:
eig函数用于计算矩阵的特征值和特征向量。对于一个 \(n\) 阶方阵 \(A\),如果存在一个非零向量 \(x\) 和一个标量 \(\lambda\),使得 \(Ax = \lambda x\),则称 \(\lambda\) 是矩阵 \(A\) 的特征值,\(x\) 是矩阵 \(A\) 对应于特征值 \(\lambda\) 的特征向量。 - 语法:
e = eig(A):返回矩阵A的所有特征值组成的向量。[V, D] = eig(A):返回矩阵A的特征向量矩阵V和特征值对角矩阵D,其中V的每一列是一个特征向量,D的主对角线元素是对应的特征值。
- 示例:
A = [1, 2; 3, 4];
e = eig(A);
disp(e);
[V, D] = eig(A);
disp(V);
disp(D);
- 应用场景:特征值和特征向量在许多领域都有广泛的应用,如动力学系统分析、图像处理、数据降维(如主成分分析)等。
总结 【5★】
inv函数用于计算矩阵的逆矩阵。det函数用于计算矩阵的行列式。linsolve函数用于求解线性方程组。eig函数用于计算矩阵的特征值和特征向量。
这些函数在矩阵运算和线性代数中都有各自独特的用途,根据具体的问题需求选择合适的函数进行计算。
第8章 符号计算
factor因式分解
在MATLAB中,factor 函数主要用于对整数进行分解质因数操作,下面为你详细介绍其语法及使用示例。
基本语法
F = factor(X)
- 输入参数:
X:可以是一个标量整数、整数向量或者整数矩阵。当X是向量或矩阵时,factor函数会对其中的每个元素分别进行质因数分解。
- 输出参数:
F:如果X是标量整数,F是一个包含X的质因数的向量,这些质因数按升序排列。如果X是向量或矩阵,F是一个元胞数组,其中每个元胞对应X中相应位置元素的质因数分解结果。
使用示例
对标量整数进行质因数分解
X = 24;
F = factor(X);
disp(F);
在这个例子中,factor 函数会将整数 24 分解为质因数,结果存储在向量 F 中。运行代码后,你会看到输出为 2 2 2 3,这表明 24 = 2 × 2 × 2 × 3。
对整数向量进行质因数分解
X = [12, 15];
F = factor(X);
disp(F);
当输入是一个向量时,factor 函数会对向量中的每个元素分别进行质因数分解,并将结果存储在元胞数组 F 中。对于这个例子,F{1} 是 12 的质因数分解结果 2 2 3,F{2} 是 15 的质因数分解结果 3 5。
对整数矩阵进行质因数分解
X = [16, 18; 20, 22];
F = factor(X);
disp(F);
这里输入是一个矩阵,factor 函数会对矩阵中的每个元素进行质因数分解,结果存储在元胞数组 F 中。F 中的每个元胞对应矩阵 X 中相应位置元素的质因数分解结果。
需要注意的是,factor 函数的输入必须是整数。如果输入为非整数,MATLAB 会给出错误提示。
% 1、定义xyz
syms x y z
% 2、factor(公式)
f1 = factor(x^9 - 1);
disp('1) 分解结果为:');
disp(f1);
limit求极限
在MATLAB里,limit函数主要用于计算符号表达式的极限。下面为你详细介绍它的语法和使用示例。
基本语法
1. limit(f, x, a)
此语法用于计算符号表达式f在变量x趋近于a时的极限。
syms x;
f = (x^2 - 1)/(x - 1);
a = 1;
L = limit(f, x, a);
disp(L);
在这个例子中,我们先定义了符号变量x,接着定义了符号表达式f,最后计算当x趋近于1时f的极限。运行代码后,会输出极限值2。
2. limit(f, a)
若符号表达式f中只有一个符号变量,那么可以省略变量名,直接使用此语法计算该符号表达式在该变量趋近于a时的极限。
syms t;
f = sin(t)/t;
a = 0;
L = limit(f, a);
disp(L);
这里定义了符号变量t和符号表达式f,然后计算当t趋近于0时f的极限,输出结果为1。
3. limit(f, x, a, 'right')
此语法用于计算符号表达式f在变量x从右侧趋近于a时的极限(右极限)。
syms x;
f = 1/x;
a = 0;
L = limit(f, x, a, 'right');
disp(L);
运行该代码后,会得到f在x从右侧趋近于0时的极限,结果为Inf(正无穷)。
4. limit(f, x, a, 'left')
此语法用于计算符号表达式f在变量x从左侧趋近于a时的极限(左极限)。
syms x;
f = 1/x;
a = 0;
L = limit(f, x, a, 'left');
disp(L);
运行代码后,会得到f在x从左侧趋近于0时的极限,结果为-Inf(负无穷)。
注意事项
- 要使用
limit函数,需要先使用syms函数定义符号变量。 - 当极限不存在时,
limit函数可能返回NaN(非数字)或者给出一个未定义的结果。
syms x
% (1)lim (x→4) (x^2 -6x +8)/(x^2 -5x +4)
limit1 = limit((x^2 - 6*x + 8)/(x^2 -5*x + 4), x, 4);
disp('(1)极限为:');
disp(limit1);
% (2)lim (x→0⁻) |x|/x
limit2 = limit(abs(x)/x, x, 0, 'left');
disp('(2)极限为:');
disp(limit2);
diff求导
在MATLAB中,diff函数主要用于计算数值差分,而对于符号表达式求导,需要使用diff函数结合符号工具箱。下面分别介绍数值差分和符号求导的语法及使用示例。
1. 数值差分
diff函数用于计算向量或矩阵的差分。
语法
Y = diff(X)
Y = diff(X,n)
Y = diff(X,n,dim)
- 参数说明:
X:输入的向量或矩阵。n:可选参数,指定差分的阶数,默认为1。dim:可选参数,指定沿哪个维度进行差分,对于向量,该参数可忽略;对于矩阵,dim = 1表示沿列方向差分,dim = 2表示沿行方向差分。
- 示例:
% 向量差分
x = [1, 3, 6, 10];
dy = diff(x);
disp(dy);
% 二阶差分
d2y = diff(x, 2);
disp(d2y);
% 矩阵差分
A = [1, 2, 3; 4, 5, 6];
dy_col = diff(A, 1, 1); % 沿列方向一阶差分
dy_row = diff(A, 1, 2); % 沿行方向一阶差分
disp(dy_col);
disp(dy_row);
2. 符号求导
使用diff函数结合符号工具箱可以对符号表达式进行求导。
语法
Y = diff(f)
Y = diff(f, var)
Y = diff(f, var, n)
- 参数说明:
f:输入的符号表达式。var:可选参数,指定对哪个符号变量求导,若省略,则对默认的符号变量求导。n:可选参数,指定求导的阶数,默认为1。
- 示例:
% 定义符号变量
syms x;
% 定义符号表达式
f = x^3 + 2*x^2 + 3*x + 4;
% 对默认变量 x 求一阶导数
df = diff(f);
disp(df);
% 对指定变量 x 求二阶导数
d2f = diff(f, x, 2);
disp(d2f);
总结
diff函数用于数值差分,计算向量或矩阵元素之间的差值。- 结合符号工具箱,
diff函数可以对符号表达式进行求导。在使用符号求导时,需要先使用syms函数定义符号变量。
syms x
% 定义函数 y
y = sin(x) - x^2 / 2;
% 求一阶导数 y'
y_prime = diff(y, x);
disp('一阶导数 y'' 为:');
disp(y_prime);
% 求二阶导数 y''
y_double_prime = diff(y, x, 2);
disp('二阶导数 y'''' 为:');
disp(y_double_prime);
% 求三阶导数 y'''
y_double_prime = diff(y, x, 3);
disp('三阶导数 y'''''' 为:');
disp(y_double_prime);
求非线性方程组的符号解
在MATLAB里,有多种方法可以求解非线性方程组,下面为你介绍两种常用的函数及其语法和使用示例。
1. fsolve函数
fsolve函数是MATLAB中用于求解非线性方程组的常用函数,它采用数值方法寻找方程组的根。
基本语法
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
- 参数说明:
fun:表示一个函数句柄,该函数用于定义非线性方程组。此函数接收一个向量输入,返回一个包含方程组中每个方程计算结果的向量。x0:是初始猜测值向量,也就是求解方程组时的起始点。合适的初始猜测值对求解结果和收敛速度有重要影响。options:是可选参数,为优化选项结构体,可用于设置求解过程中的各种参数,例如最大迭代次数、误差容限等。
使用示例
假设要求解如下非线性方程组:
[
\begin{cases}
x_1^2 + x_2^2 - 1 = 0 \
x_1 - x_2^2 = 0
\end{cases}
]
% 定义非线性方程组的函数
function F = myfun(x)
F(1) = x(1)^2 + x(2)^2 - 1;
F(2) = x(1) - x(2)^2;
end
% 初始猜测值
x0 = [0.5; 0.5];
% 调用 fsolve 函数求解方程组
x = fsolve(@myfun, x0);
% 显示求解结果
disp('方程组的解为:');
disp(x);
2. vpasolve函数
vpasolve函数是符号工具箱中的函数,可用于求解符号形式的非线性方程组,它能给出符号解或数值近似解。
基本语法
sol = vpasolve(eqns,vars)
sol = vpasolve(eqns,vars,init_guess)
- 参数说明:
eqns:是一个符号表达式或符号表达式向量,用于定义非线性方程组。vars:是一个符号变量或符号变量向量,代表方程组中的未知变量。init_guess:是可选参数,为初始猜测值,可帮助求解器更快地收敛到解。
使用示例
同样求解上述非线性方程组:
% 定义符号变量
syms x1 x2;
% 定义非线性方程组
eqns = [x1^2 + x2^2 - 1 == 0, x1 - x2^2 == 0];
% 定义未知变量
vars = [x1, x2];
% 调用 vpasolve 函数求解方程组
sol = vpasolve(eqns, vars);
% 显示求解结果
disp('方程组的解为:');
disp(sol.x1);
disp(sol.x2);
总结
fsolve函数是数值求解器,需要将方程组定义为函数句柄,并且要提供初始猜测值。vpasolve函数是符号求解器,使用符号表达式定义方程组,可给出符号解或数值近似解,也可提供初始猜测值来加速求解过程。
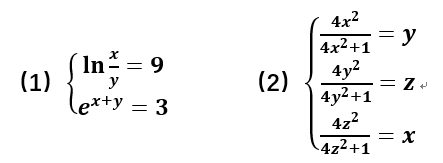
syms x y z
% 方程组 (1)
eq1_1 = log(x/y) == 9;
eq1_2 = exp(x + y) == 3;
solution1 = solve([eq1_1, eq1_2], [x, y]);
x1 = solution1.x;
y1 = solution1.y;
disp('方程组 (1) 的解为:');
disp(['x = ', char(x1)]);
disp(['y = ', char(y1)]);
% 方程组 (2)
eq2_1 = (4*x^2)/(4*x^2 + 1) == y;
eq2_2 = (4*y^2)/(4*y^2 + 1) == z;
eq2_3 = (4*z^2)/(4*z^2 + 1) == x;
solution2 = solve([eq2_1, eq2_2, eq2_3], [x, y, z]);
x2 = solution2.x;
y2 = solution2.y;
z2 = solution2.z;
disp('方程组 (2) 的解为:');
for i = 1:length(x2)
disp(['解 ', num2str(i), ':']);
disp(['x = ', char(x2(i))]);
disp(['y = ', char(y2(i))]);
disp(['z = ', char(z2(i))]);
end
利用符号表达式求z
syms x y
% 定义符号常数 x 和 y
x = sym('6');
y = sym('5');
% 定义表达式 z
z = (x + 1) / (sqrt(3 + x) - sqrt(y));
% 计算 z 的值
result = vpa(z);
disp(result);
syms a b
a=6;
b=5;
z = (a + 1) / (sqrt(3 + a) - sqrt(b));
disp(z);
化简表达式
在MATLAB里,能借助符号工具箱对表达式进行化简,下面为你介绍几个常用的化简函数及其语法与示例。
1. simplify函数
simplify函数是一个通用的化简函数,它能尝试运用多种规则对符号表达式进行化简。
语法
R = simplify(S)
- 参数说明:
S:输入的符号表达式。R:化简后的符号表达式。
示例
% 定义符号变量
syms x;
% 定义符号表达式
S = (x^2 - 1)/(x - 1);
% 化简表达式
R = simplify(S);
% 显示化简结果
disp(R);
此例中,simplify函数把表达式 (x^2 - 1)/(x - 1) 化简为 x + 1。
2. expand函数
expand函数主要用于展开表达式,像多项式展开、三角函数展开等。
语法
R = expand(S)
- 参数说明:
S:输入的符号表达式。R:展开后的符号表达式。
示例
% 定义符号变量
syms x;
% 定义符号表达式
S = (x + 1)^2;
% 展开表达式
R = expand(S);
% 显示展开结果
disp(R);
在这个例子中,expand函数把表达式 (x + 1)^2 展开为 x^2 + 2*x + 1。
3. factor函数
factor函数用于对多项式进行因式分解。
语法
R = factor(S)
- 参数说明:
S:输入的符号表达式,通常是多项式。R:因式分解后的符号表达式。
示例
% 定义符号变量
syms x;
% 定义符号表达式
S = x^2 - 1;
% 因式分解表达式
R = factor(S);
% 显示因式分解结果
disp(R);
这里,factor函数把表达式 x^2 - 1 因式分解为 (x - 1)*(x + 1)。
4. collect函数
collect函数可将表达式按照指定变量的幂次进行合并同类项。
语法
R = collect(S,v)
- 参数说明:
S:输入的符号表达式。v:指定的变量。R:合并同类项后的符号表达式。
示例
% 定义符号变量
syms x;
% 定义符号表达式
S = x^2 + 3*x + 2*x^2;
% 按 x 的幂次合并同类项
R = collect(S,x);
% 显示合并结果
disp(R);
此例中,collect函数把表达式 x^2 + 3*x + 2*x^2 合并为 3*x^2 + 3*x。
在使用这些函数之前,要先运用syms函数定义符号变量。并且,不同的化简函数适用于不同的场景,你可以依据表达式的特点选择合适的函数。
syms beta1 beta2 x
% (1)化简 sin(beta1)*cos(beta2) - cos(beta1)*sin(beta2)
expr1 = sin(beta1)*cos(beta2) - cos(beta1)*sin(beta2);
simplified_expr1 = simplify(expr1);
disp('(1)化简结果为:');
disp(simplified_expr1);
% (2)化简 (4x^2 + 8x + 3)/(2x + 1)
expr2 = (4*x^2 + 8*x + 3)/(2*x + 1);
simplified_expr2 = simplify(expr2);
disp('(2)化简结果为:');
disp(simplified_expr2);


 浙公网安备 33010602011771号
浙公网安备 33010602011771号