数据结构笔记 第五章 树与二叉树

第五章 树与二叉树

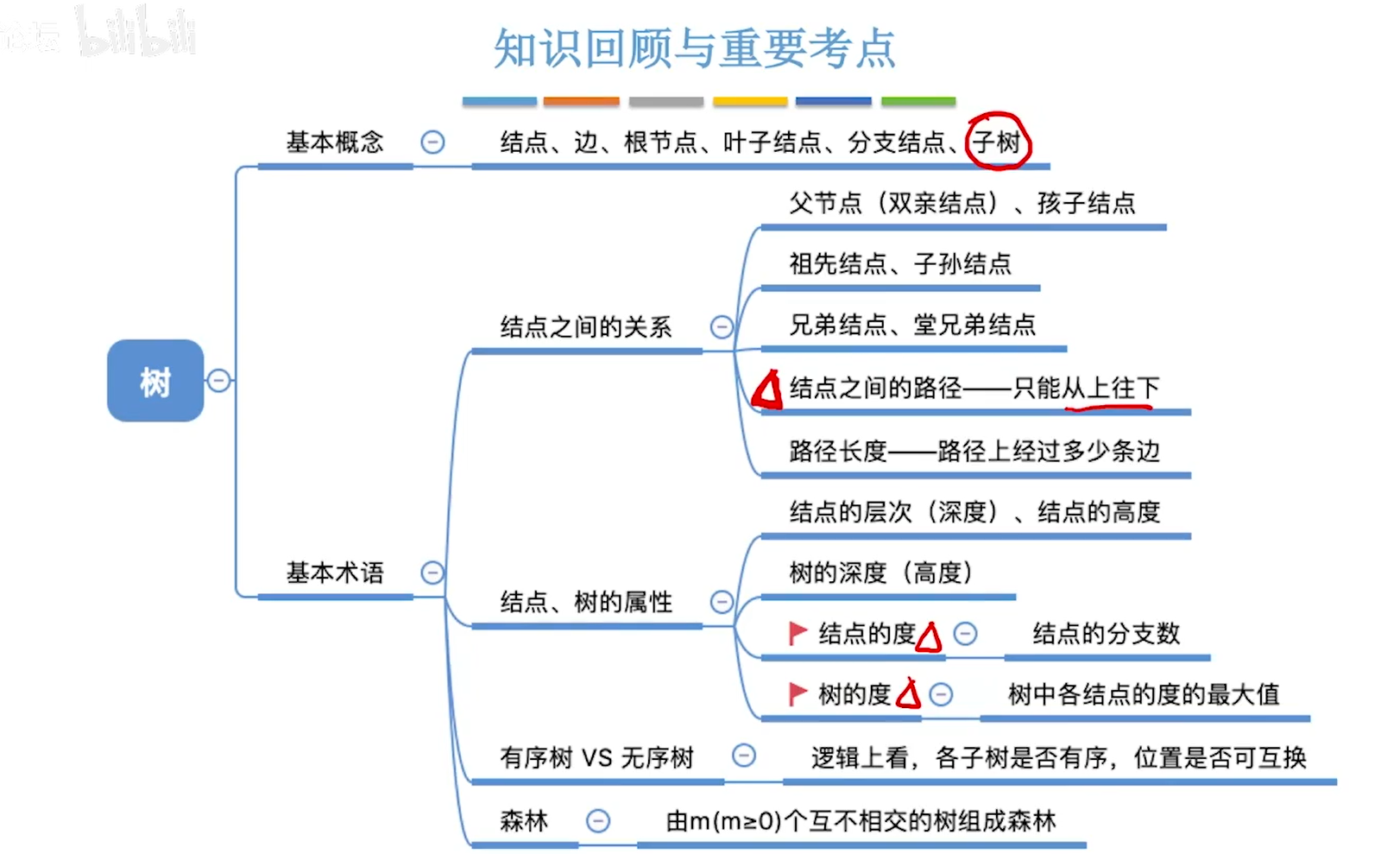
5.1树的基本概念

5.1.1树的定义

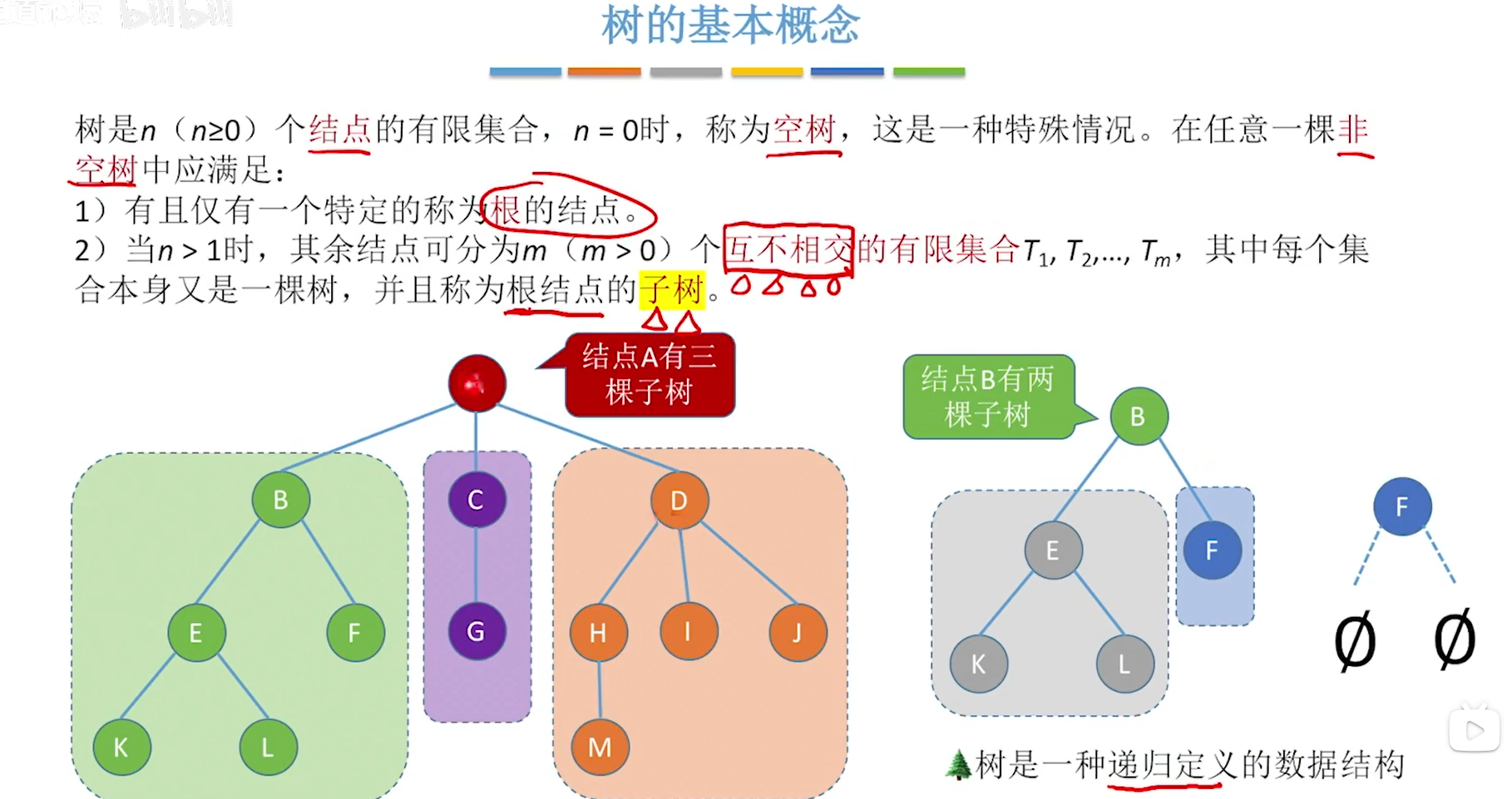
5.1.2基本术语


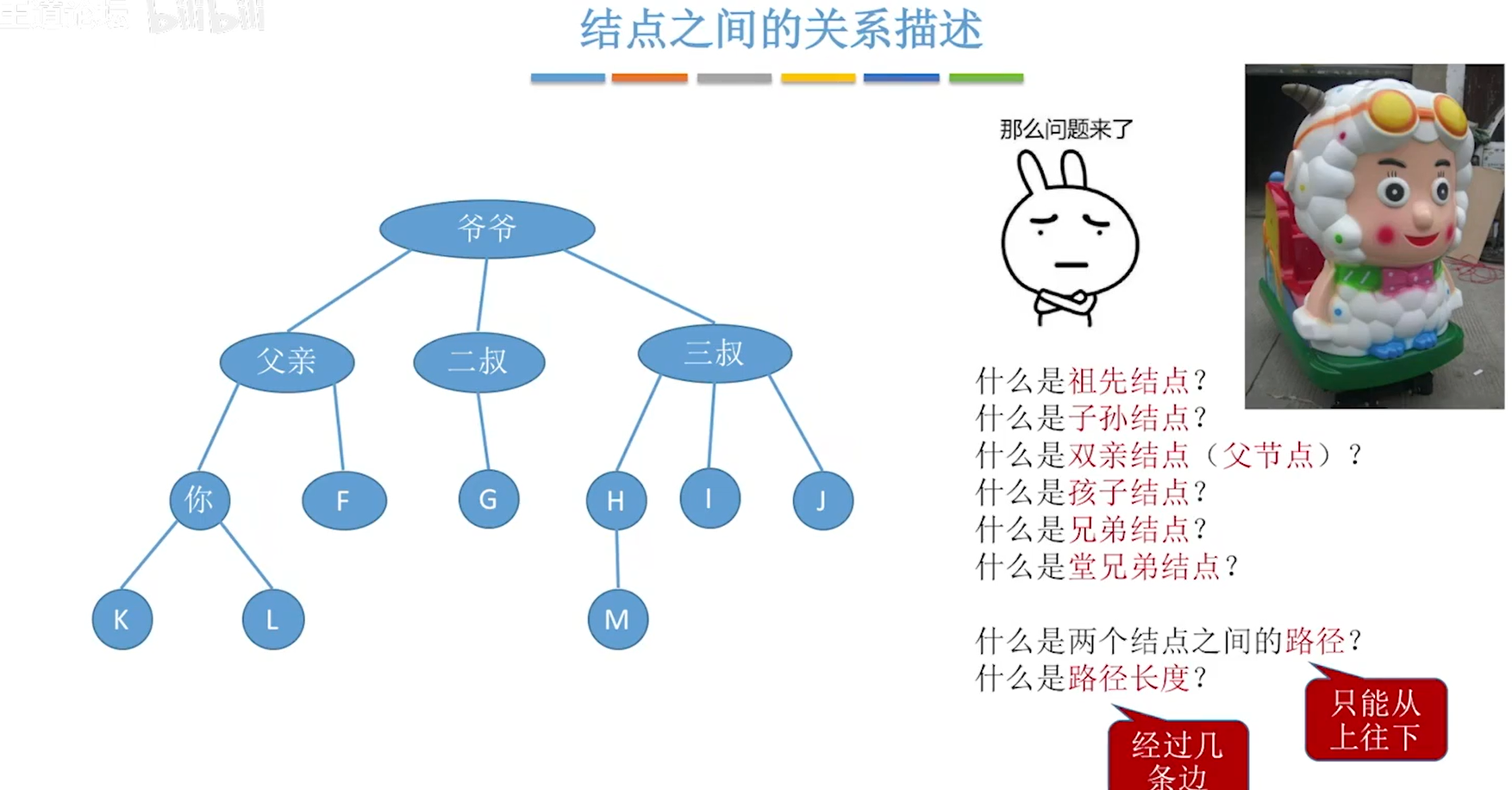
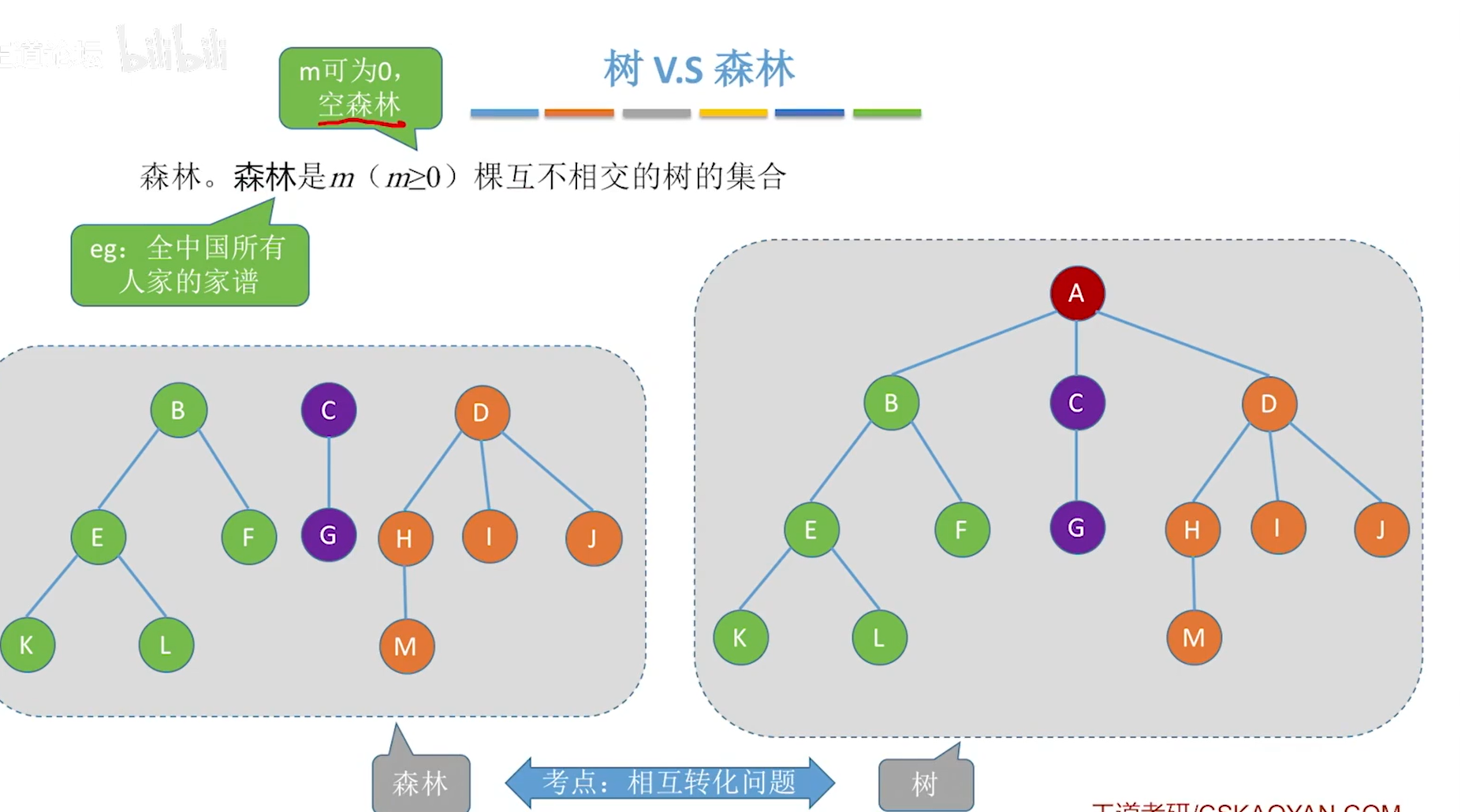
5.1树的基本概念小结

5.2树的性质以及常考点

基本性质

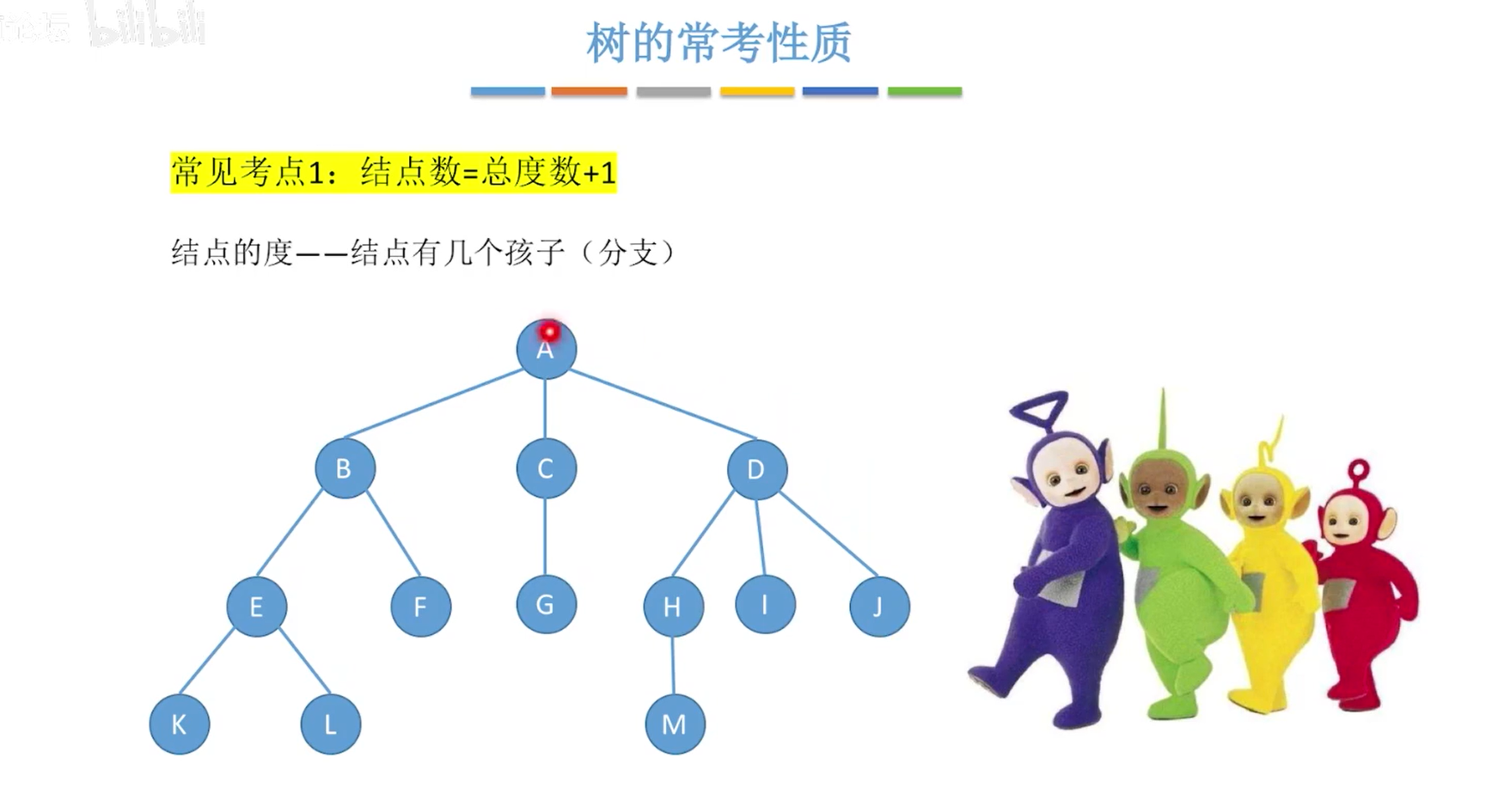
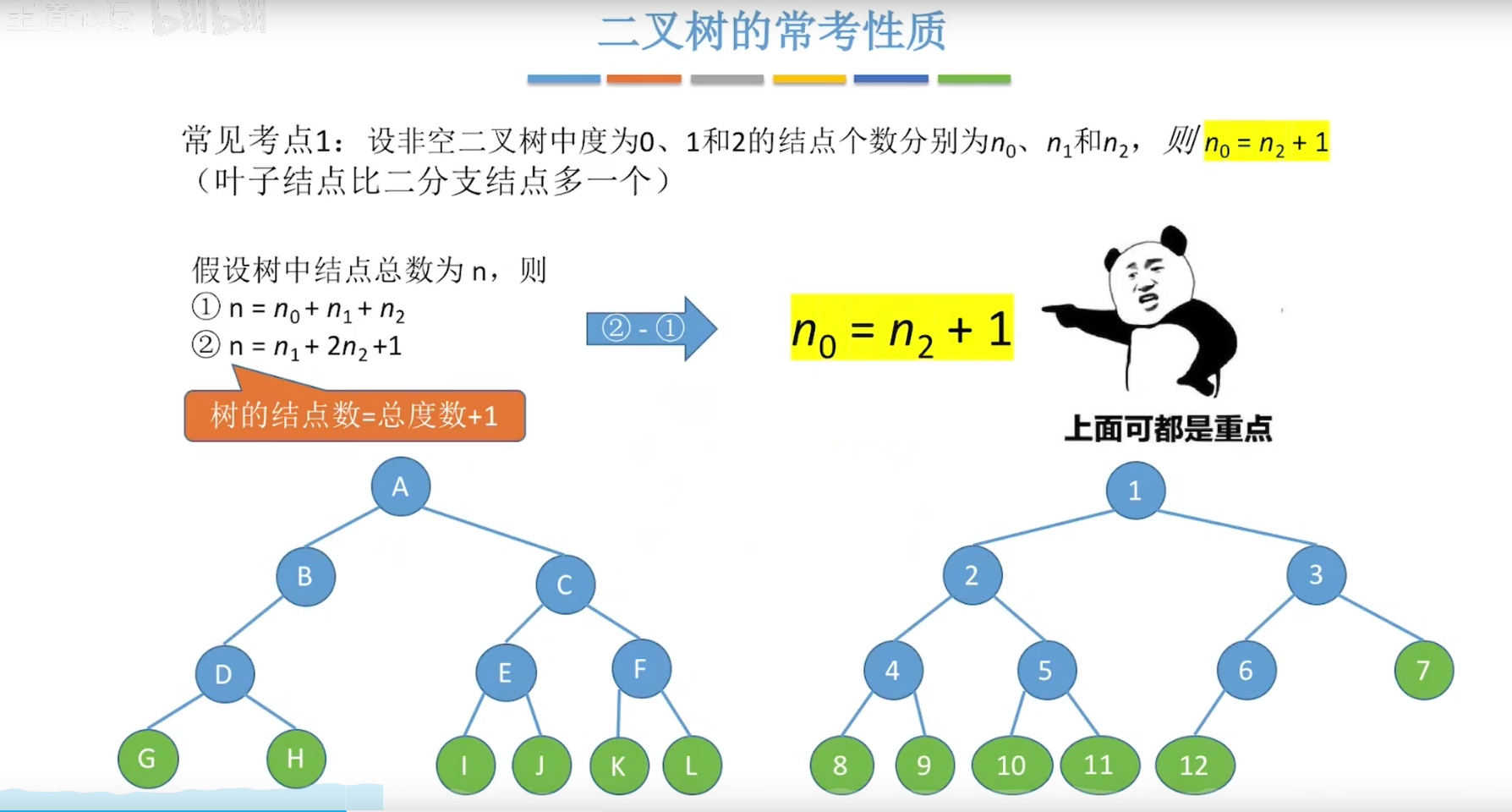
• 树中的结点数等于所有节点的度数之和+1.
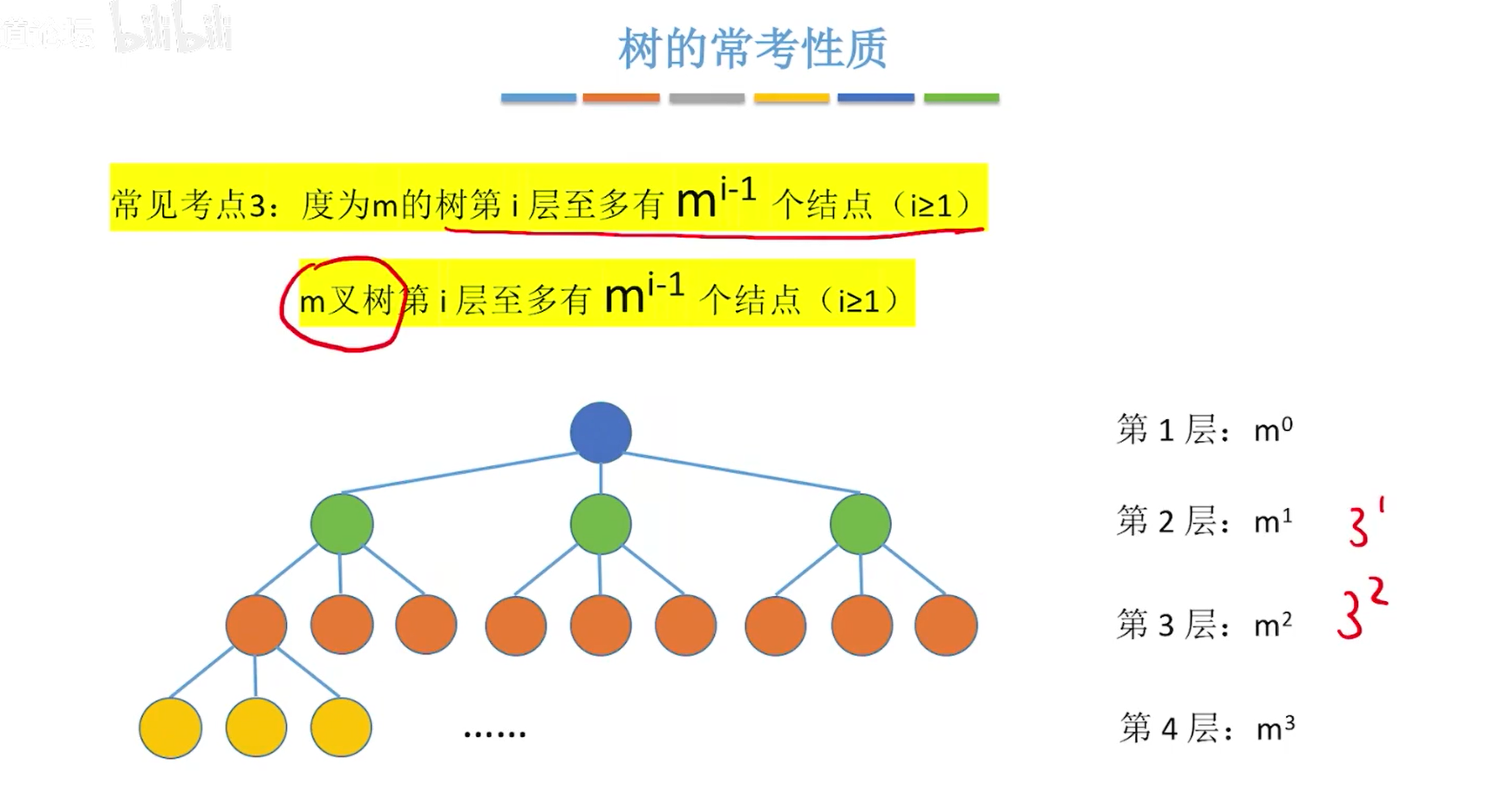
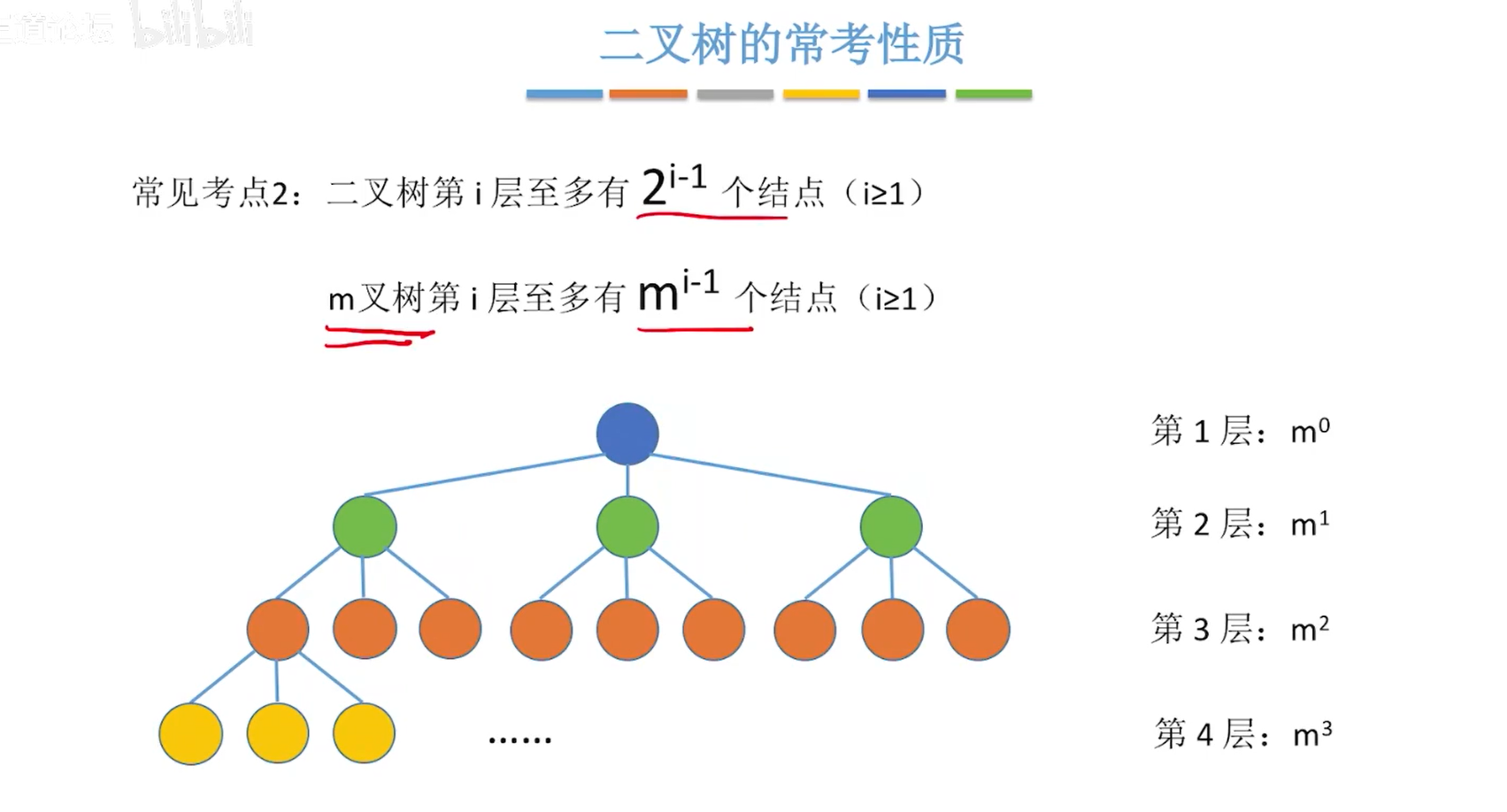
• 度为m的数中第i层上至多有m的（i-1）次方个结点（i>=1）
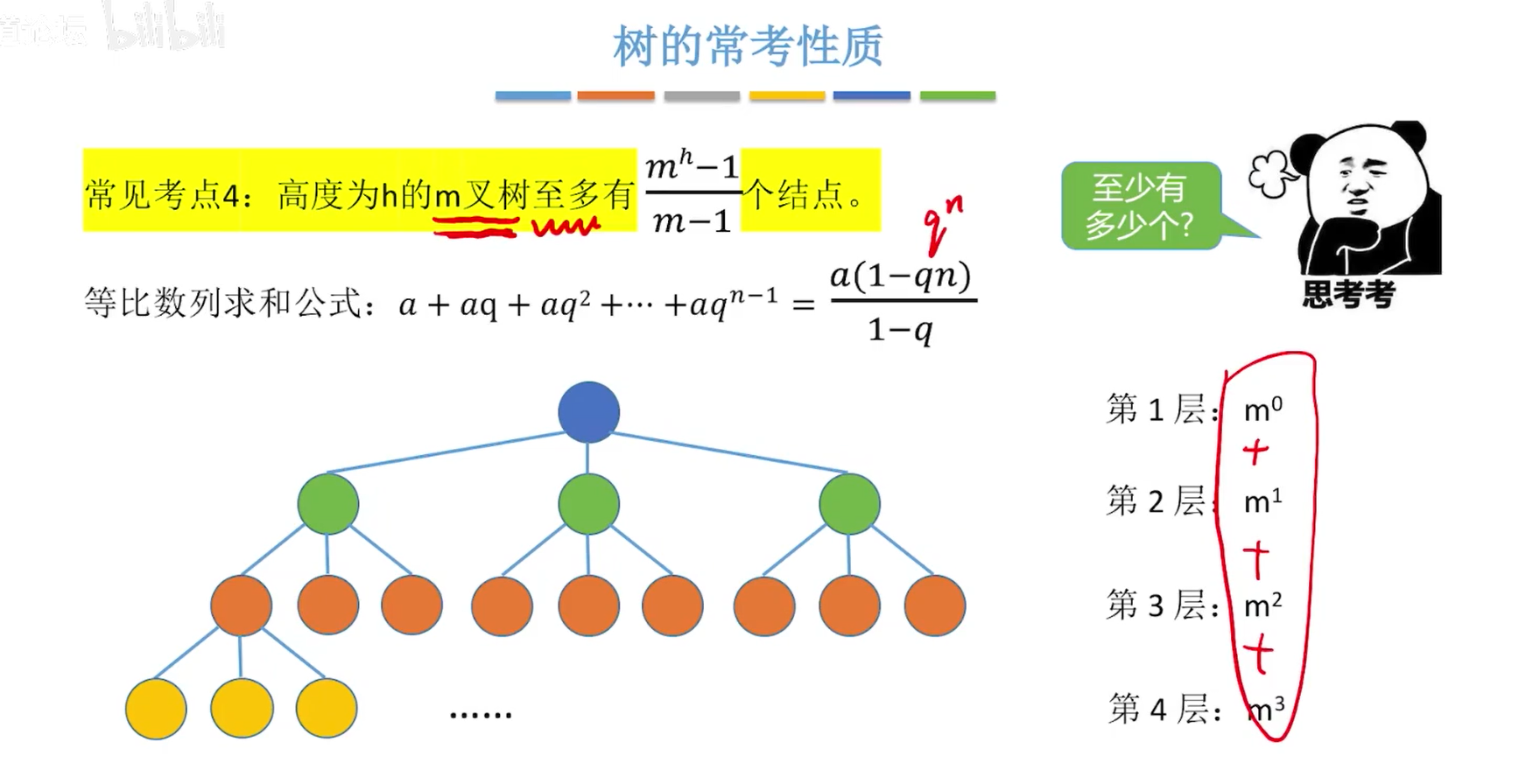
• 高度为h的m叉树至多有（m的h次方-1）/（m-1）个结点
• 具有n个结点的m叉树的最小高度为【logm（n（m-1）+1）】

常考点

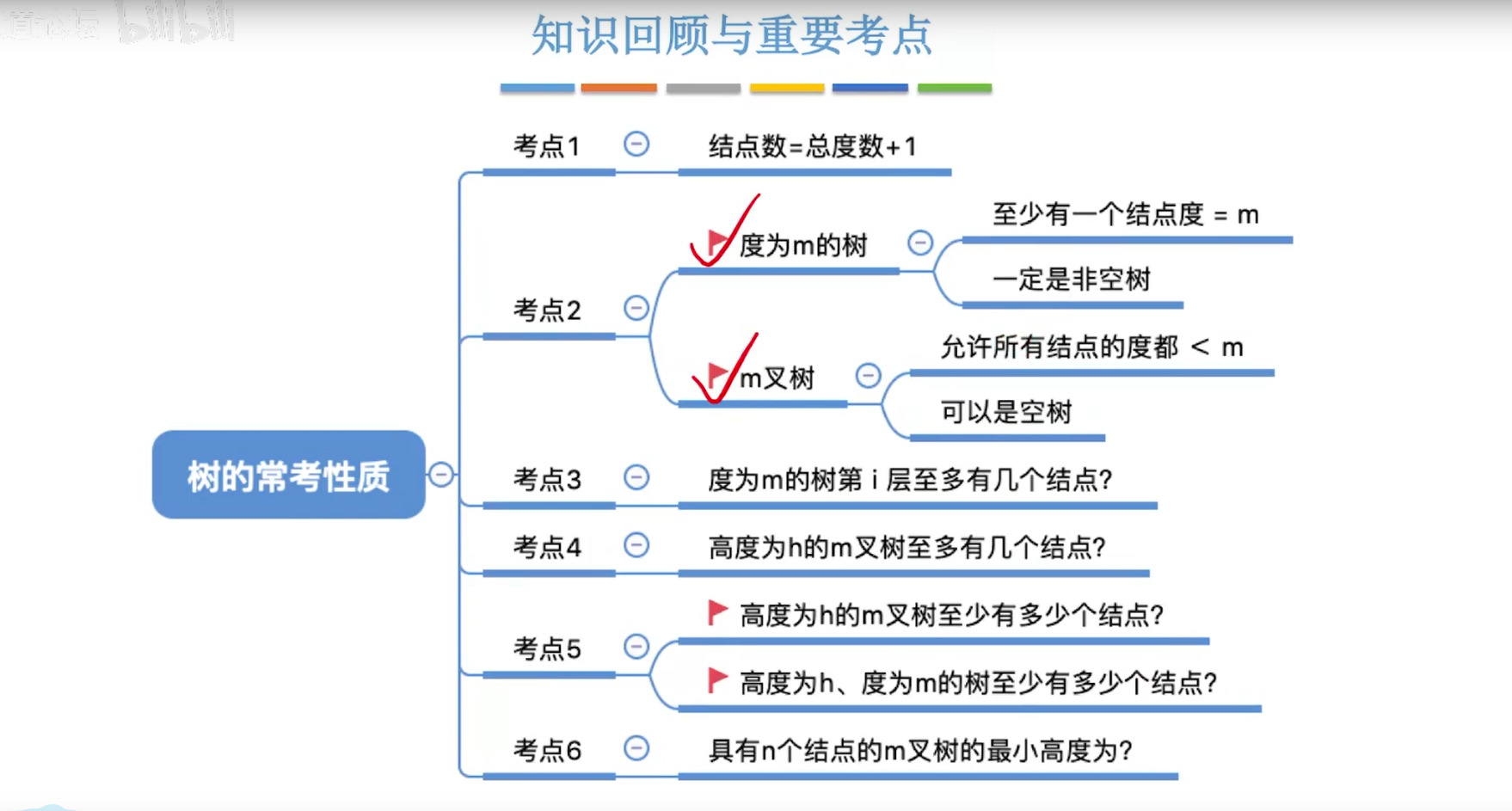
考点一 ：结点数=总度数+1

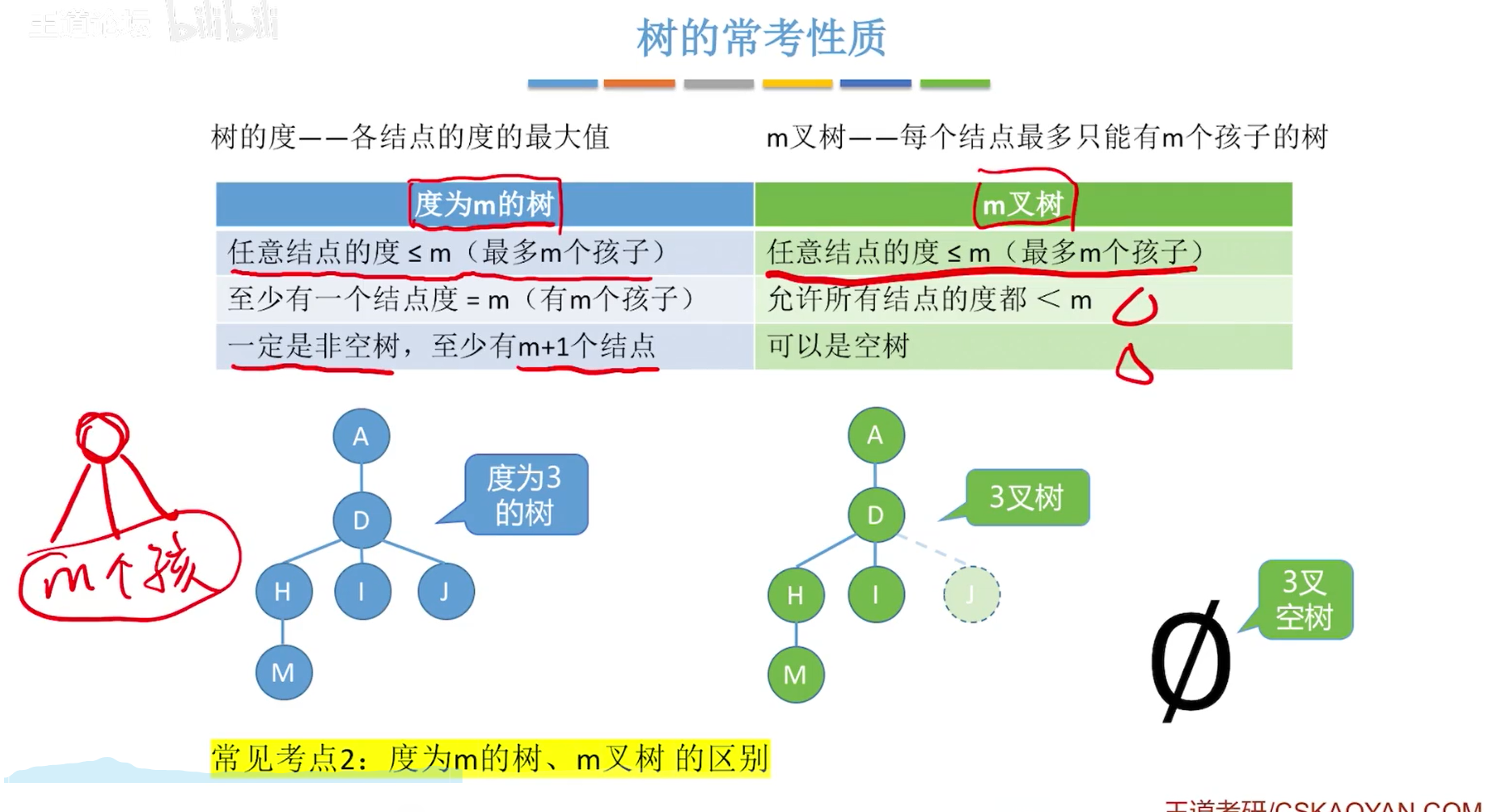
考点二

考点三

考点四

考点五

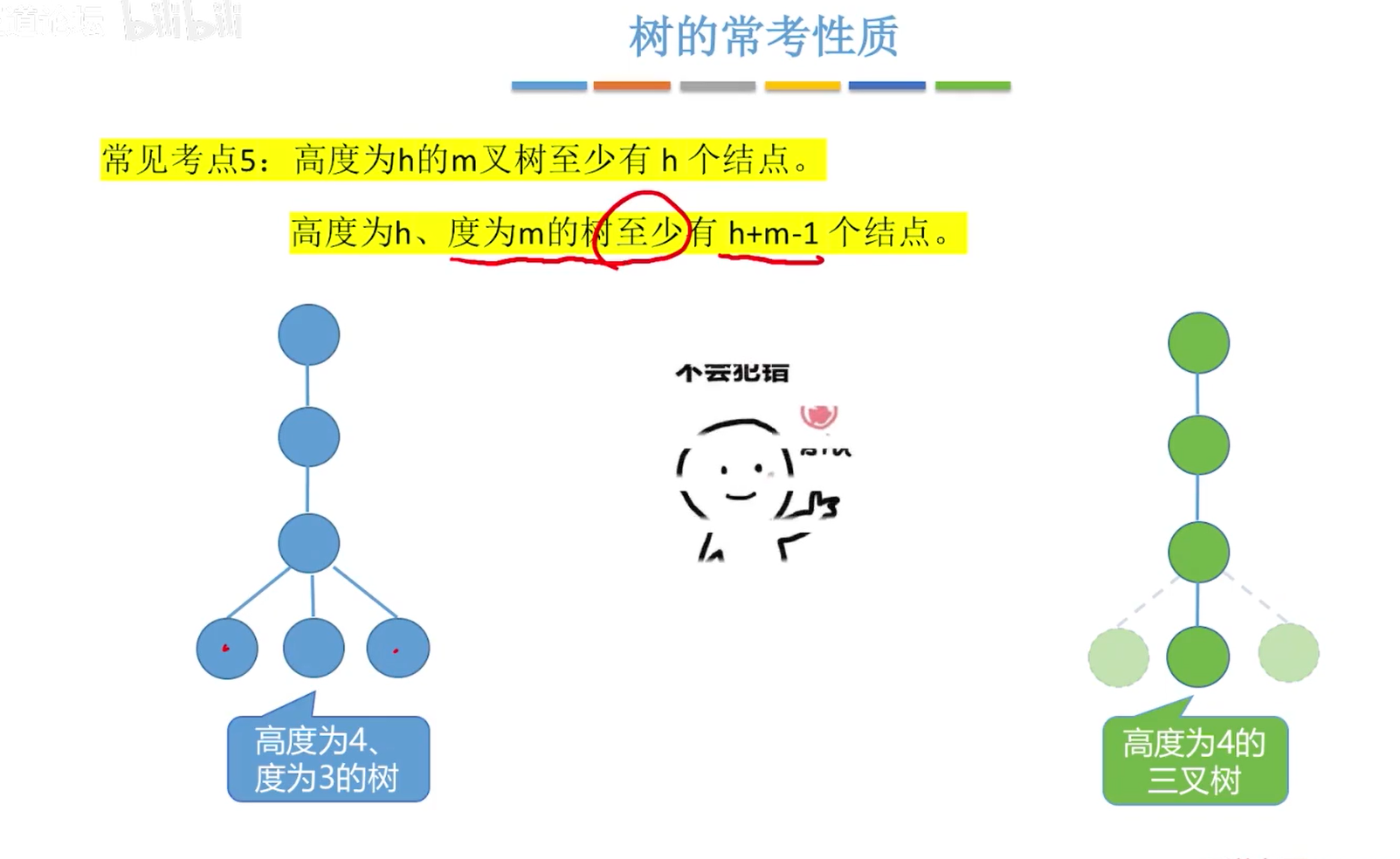
考点六

树的性质小结

5.3二叉树的概念

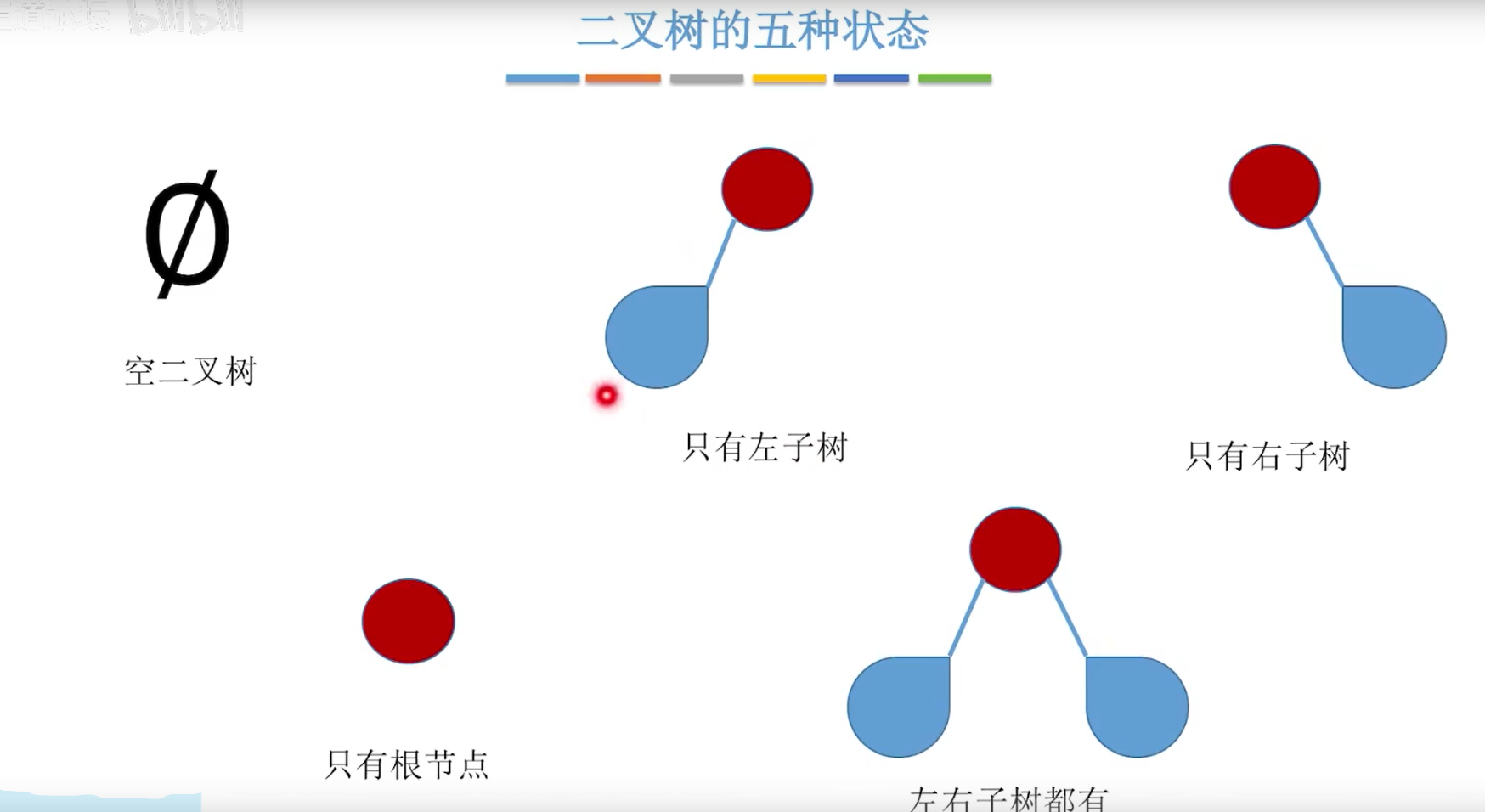
5.3.1二叉树的定义

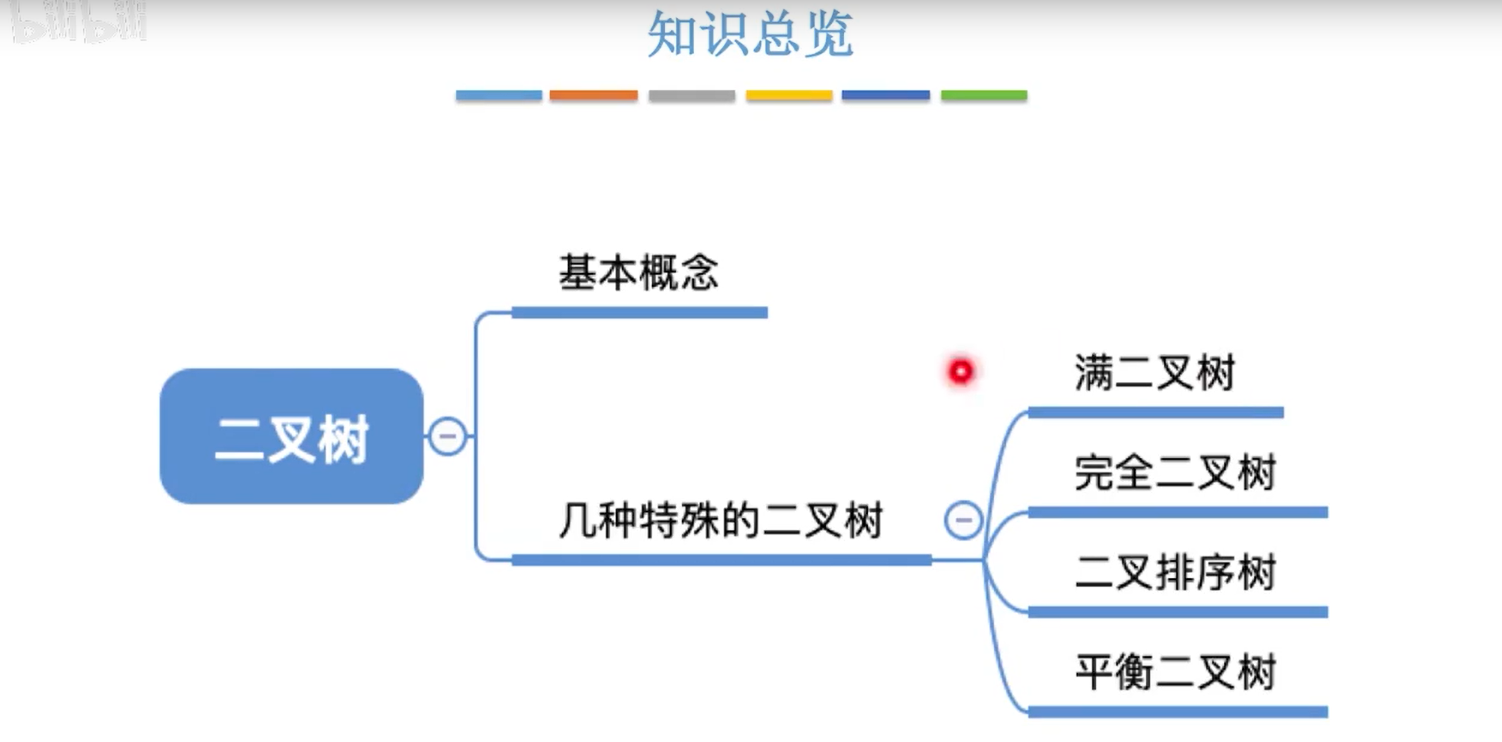
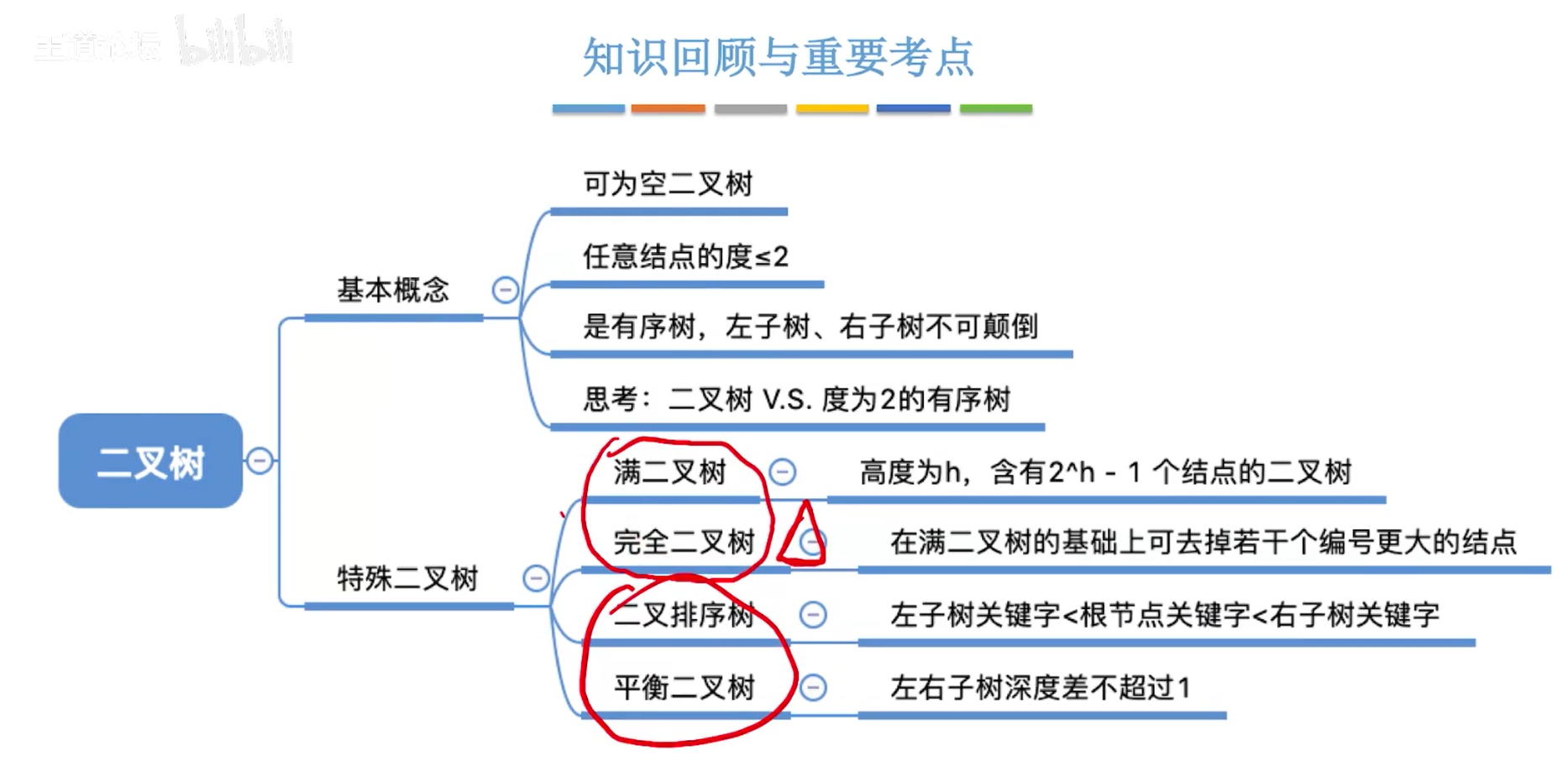
5.3.2特殊的二叉树

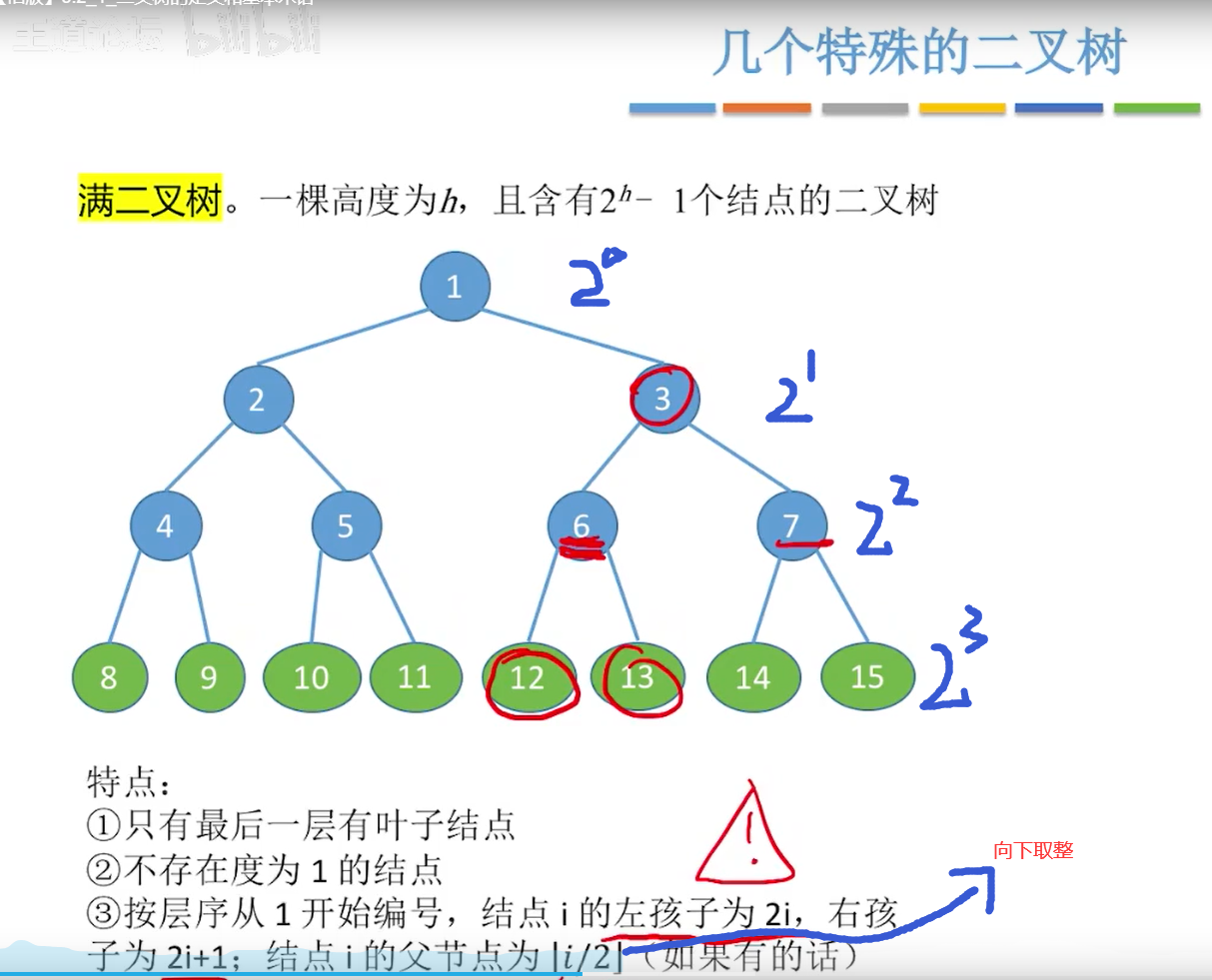
• 满二叉树

  

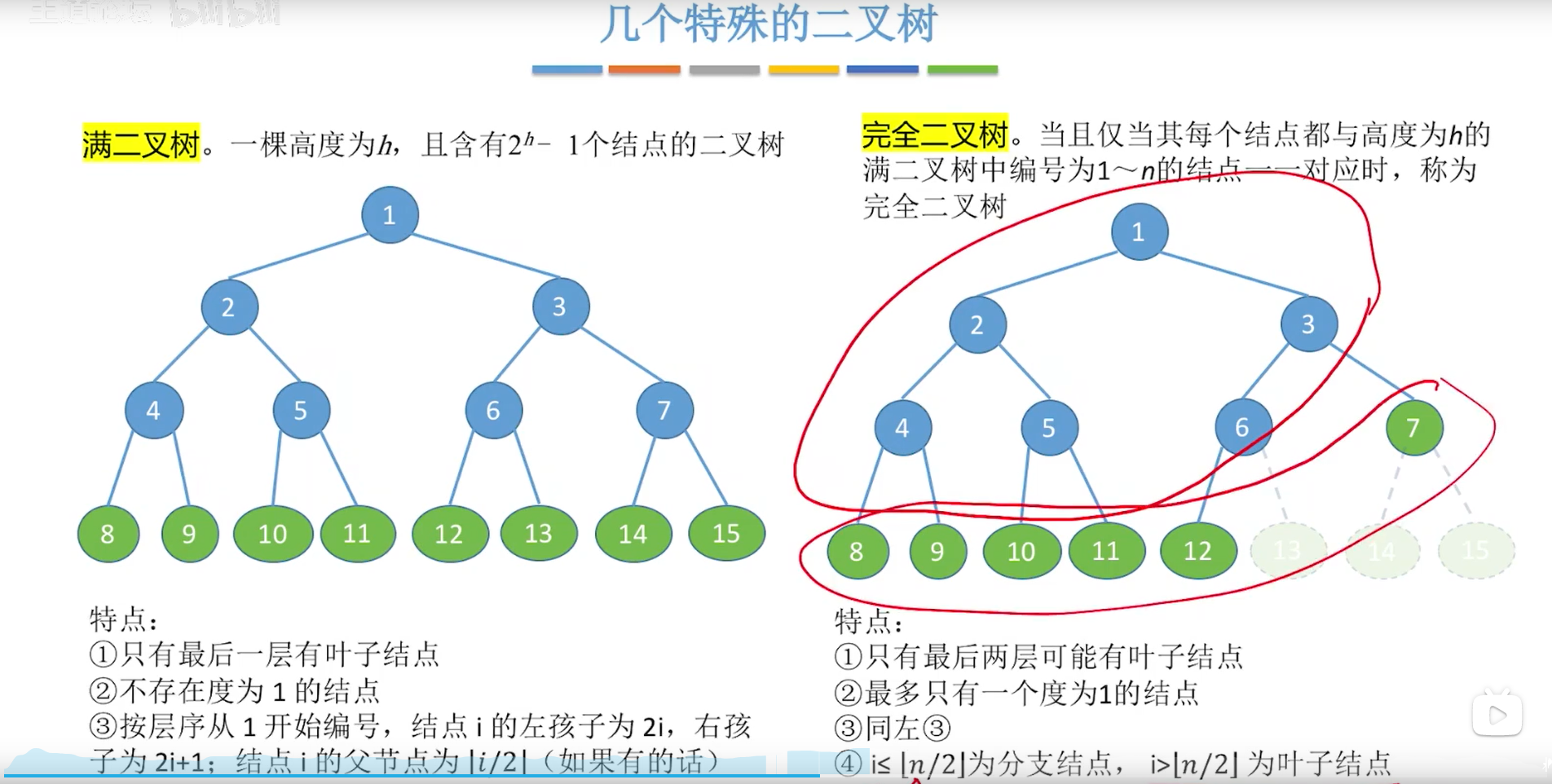
完全二叉树

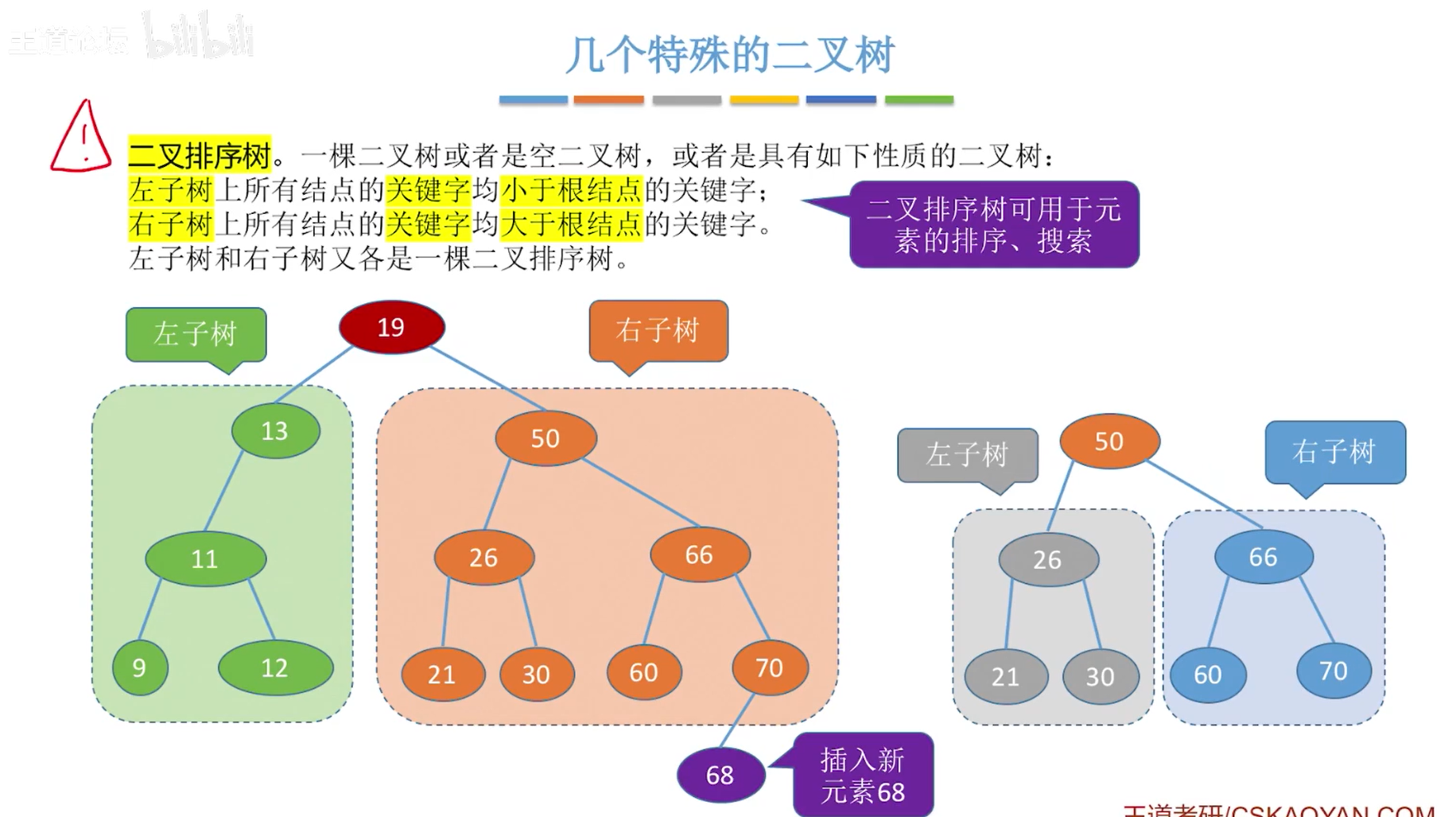
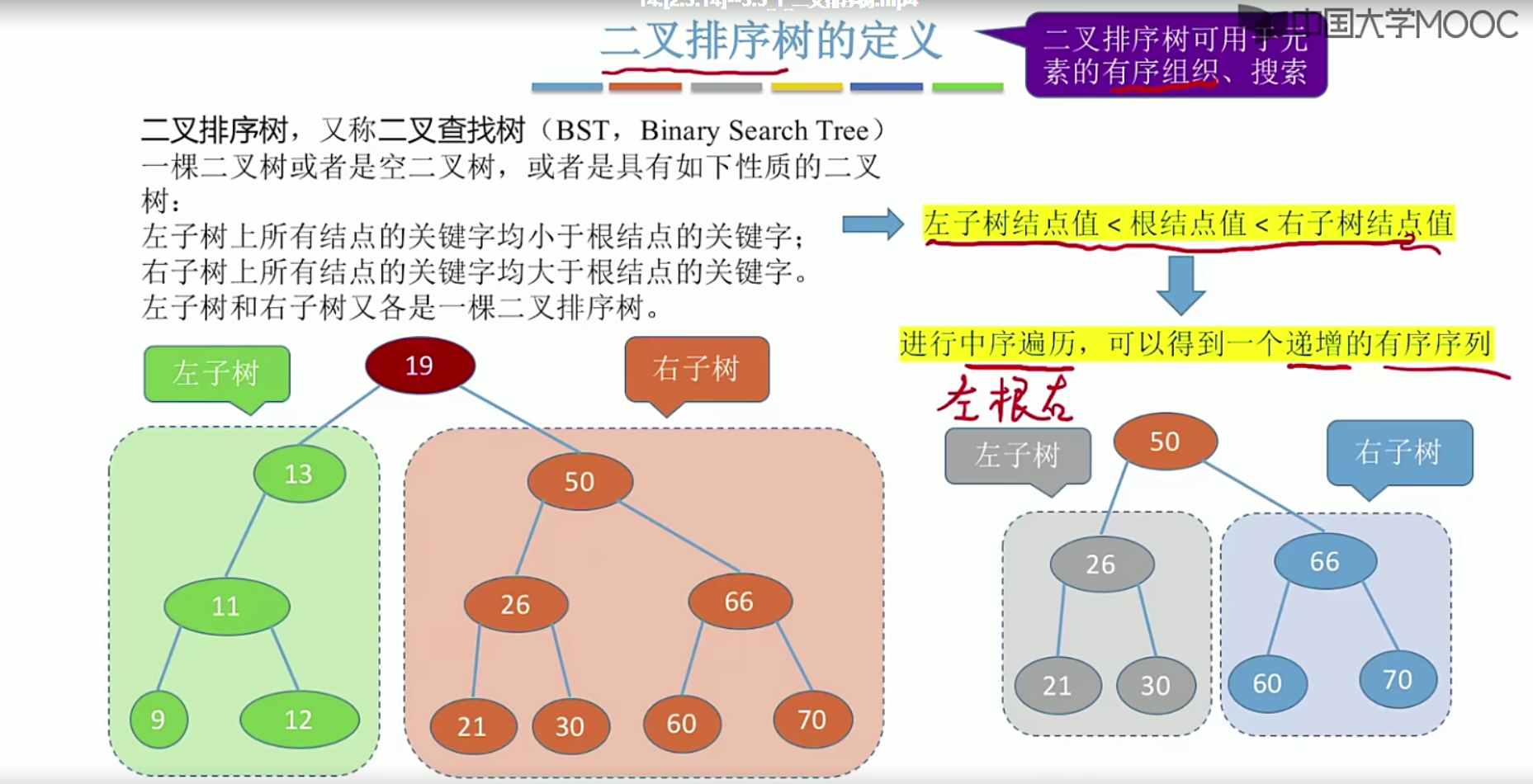
二叉排序树

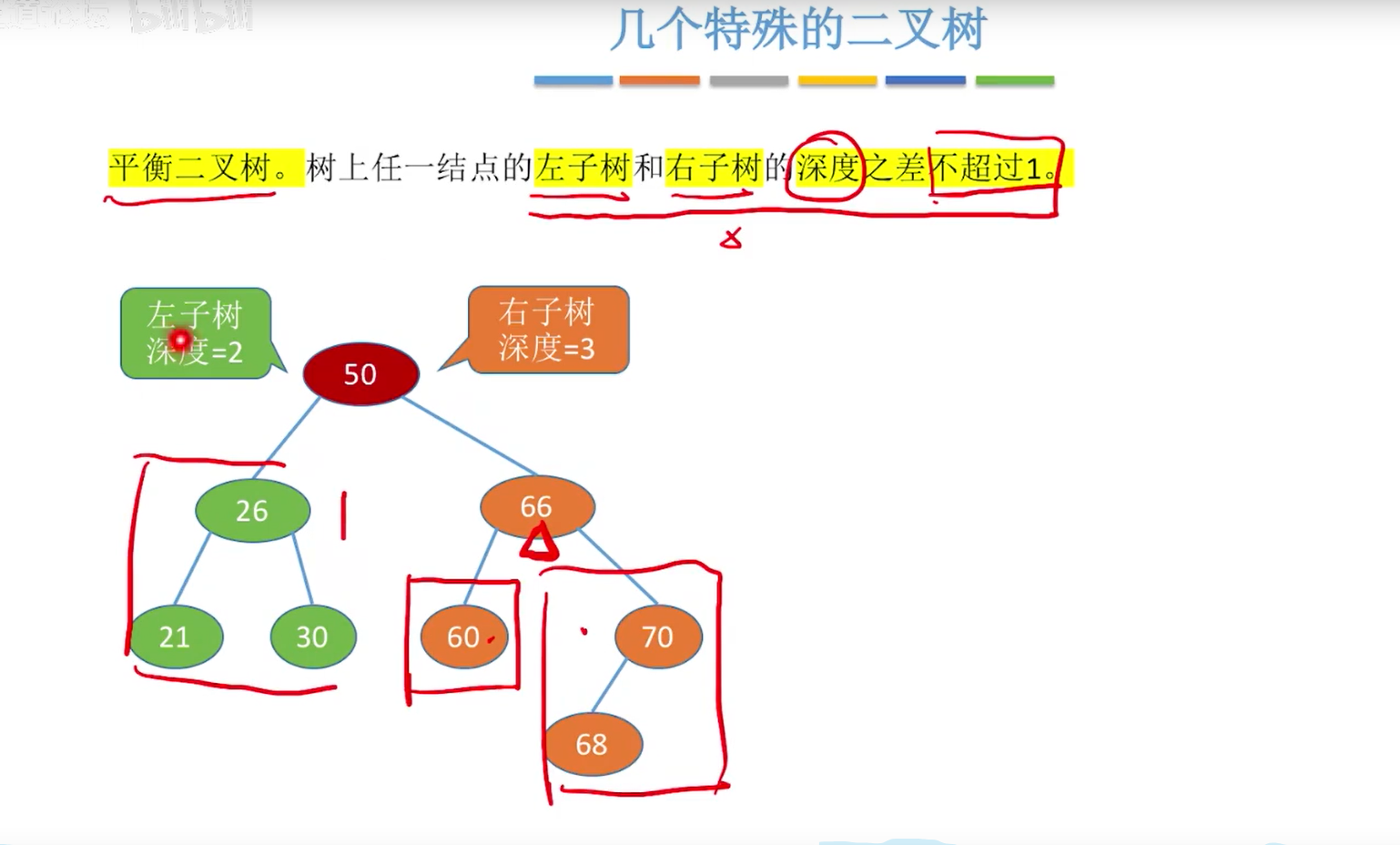
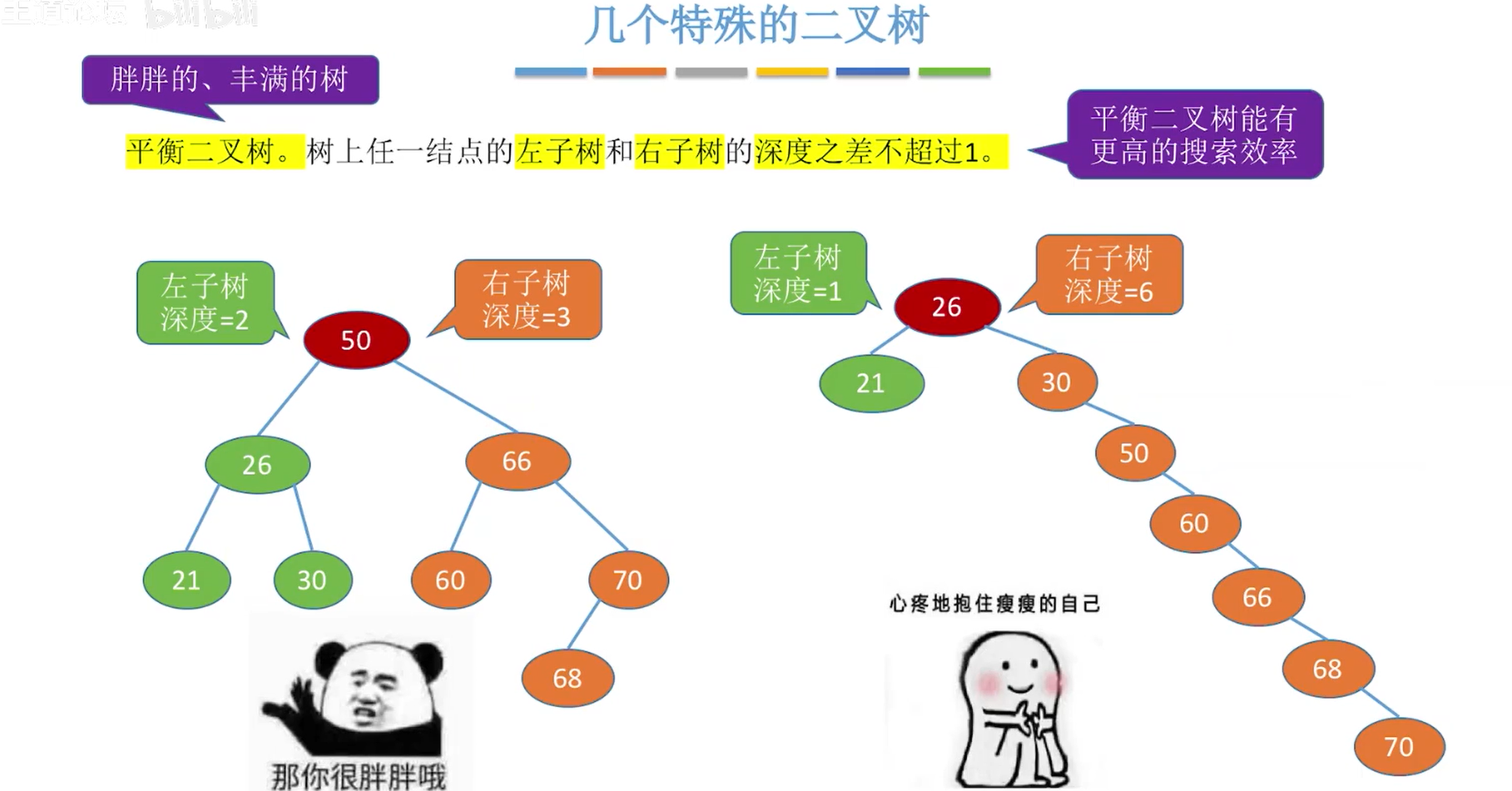
平衡二叉树

5.3.3 二叉树概念小结

5.4 二叉树的性质与常考点

考点一

考点二

考点三

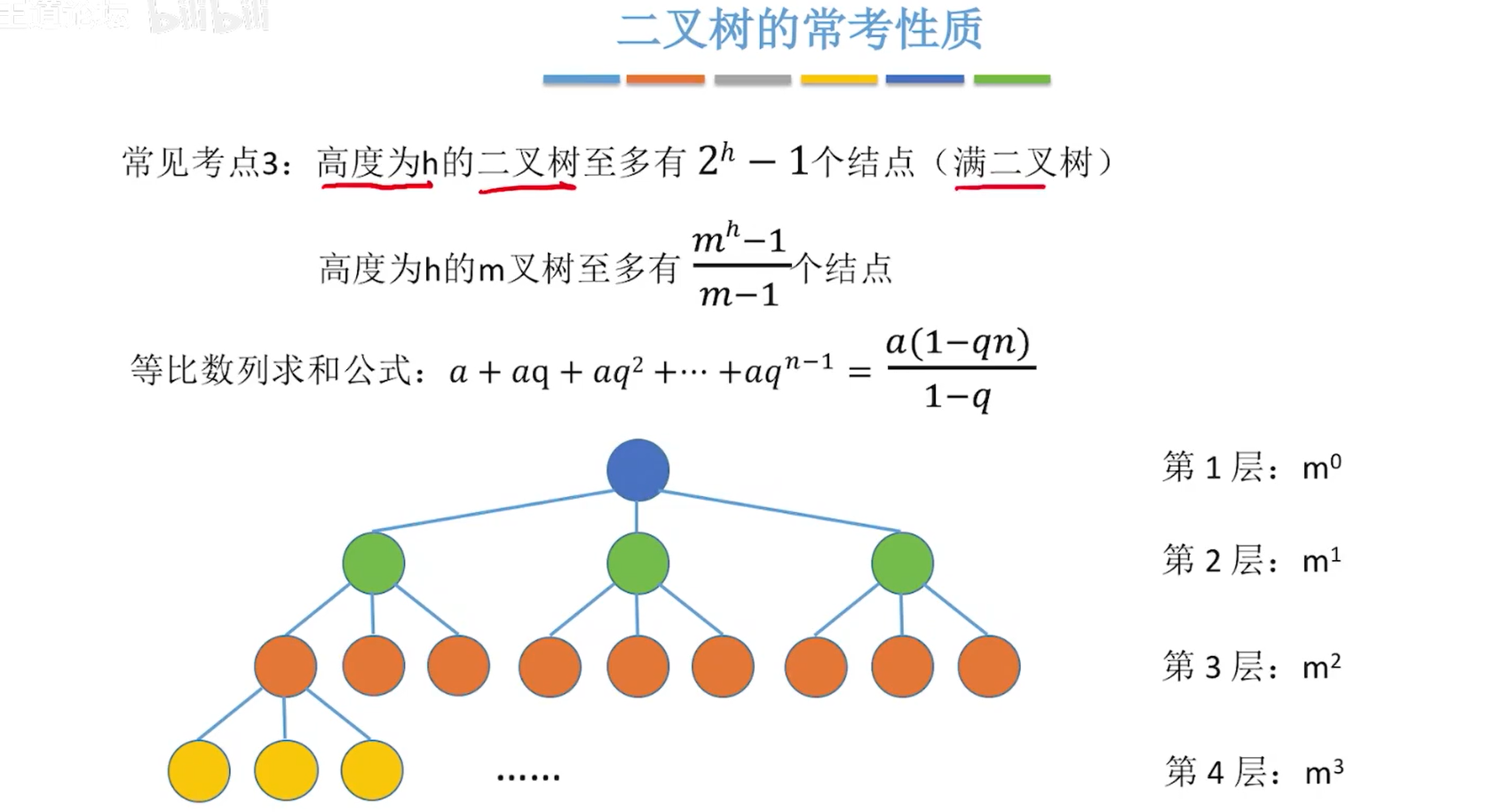
完全二叉树考点

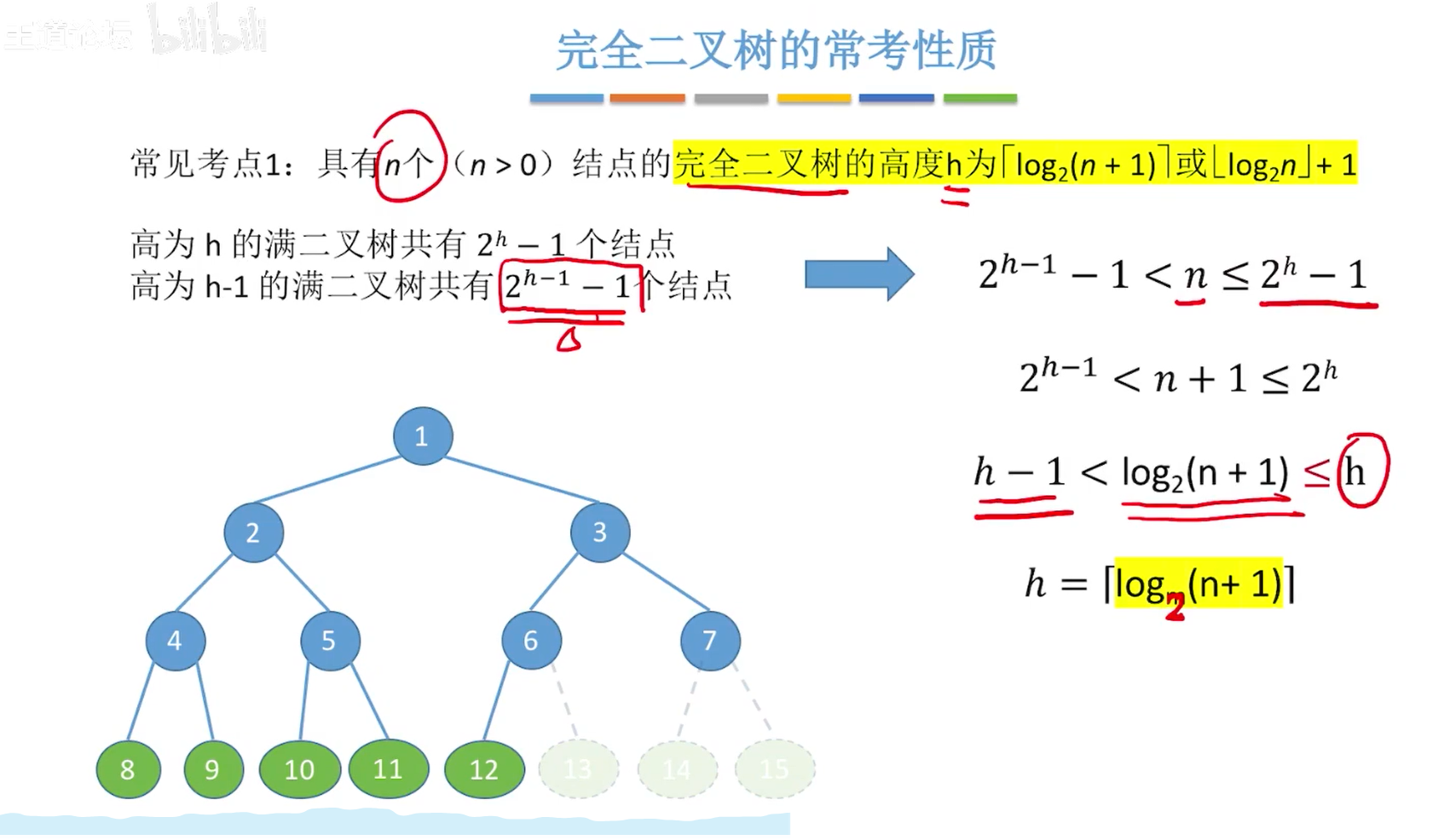
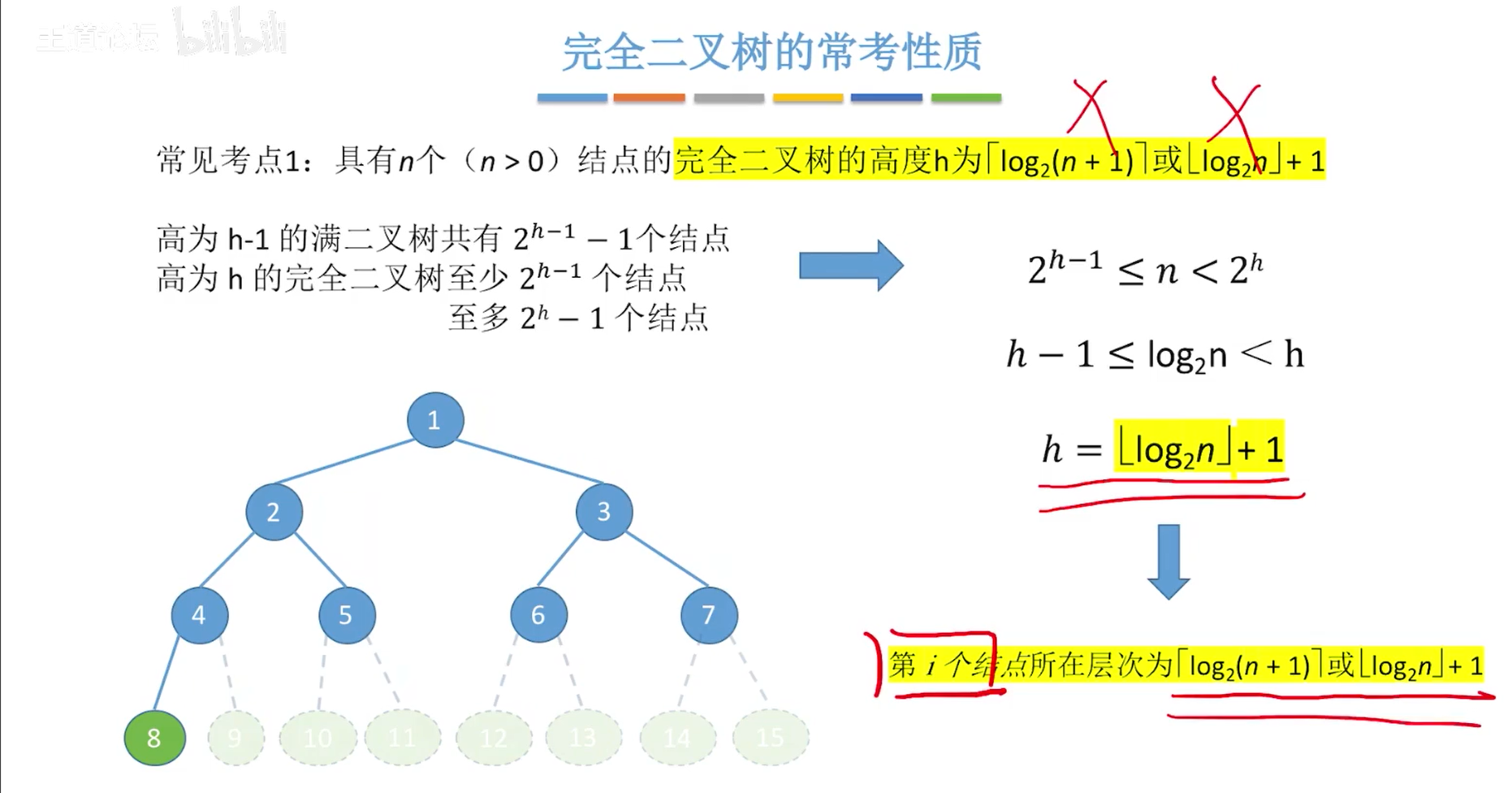
完全二叉树考点二

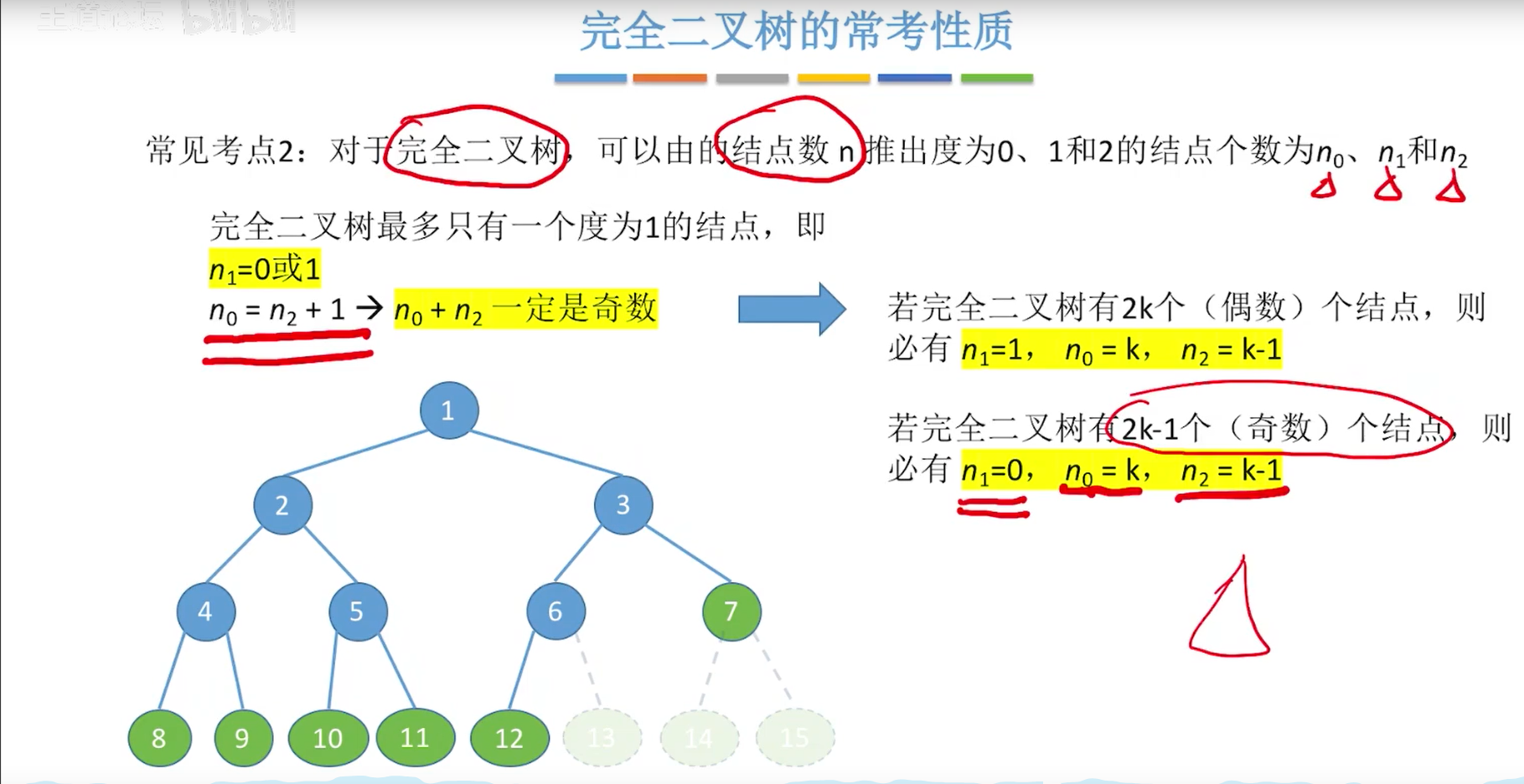
考点小结

5.5二叉树的存储结构

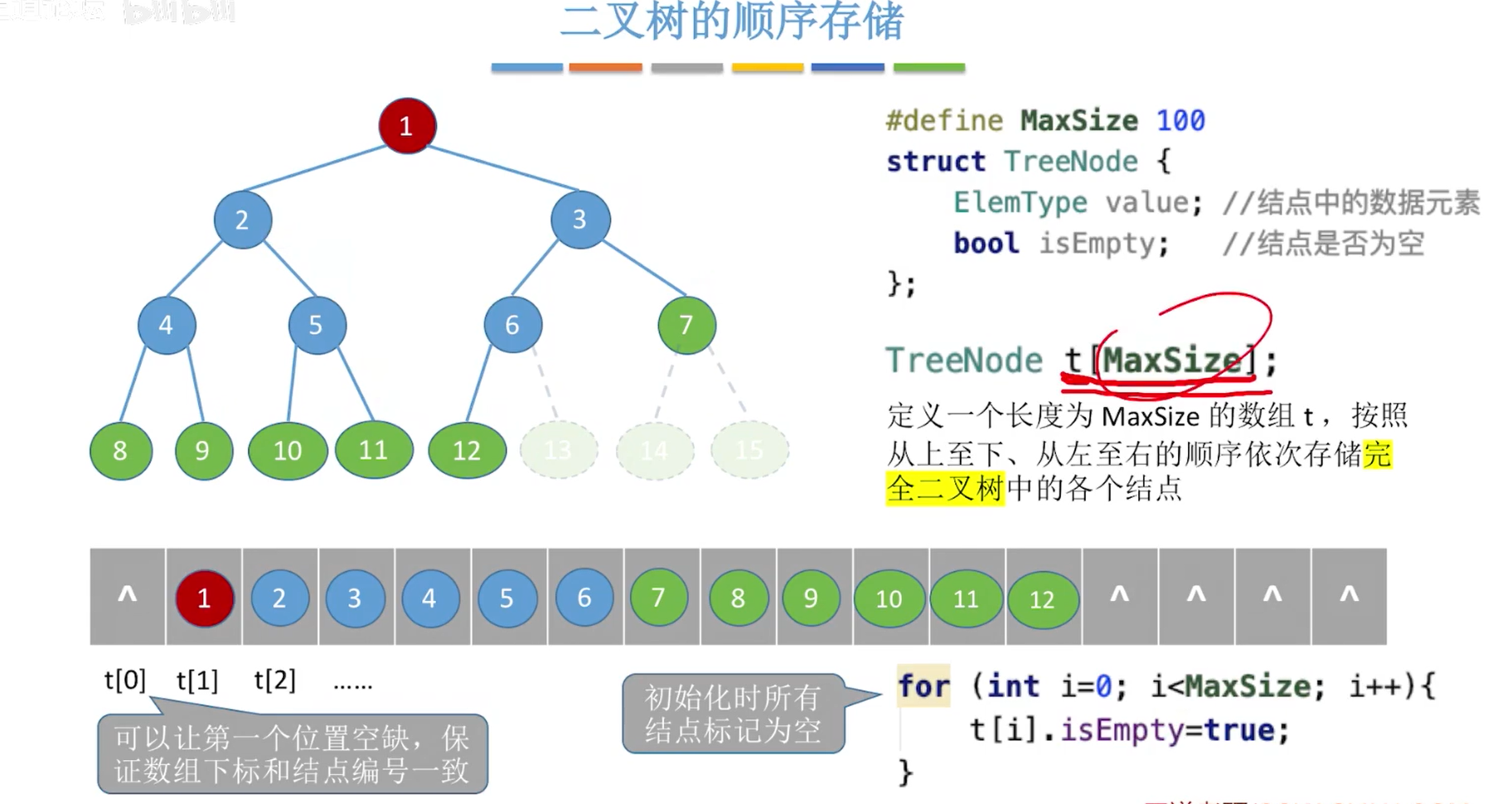
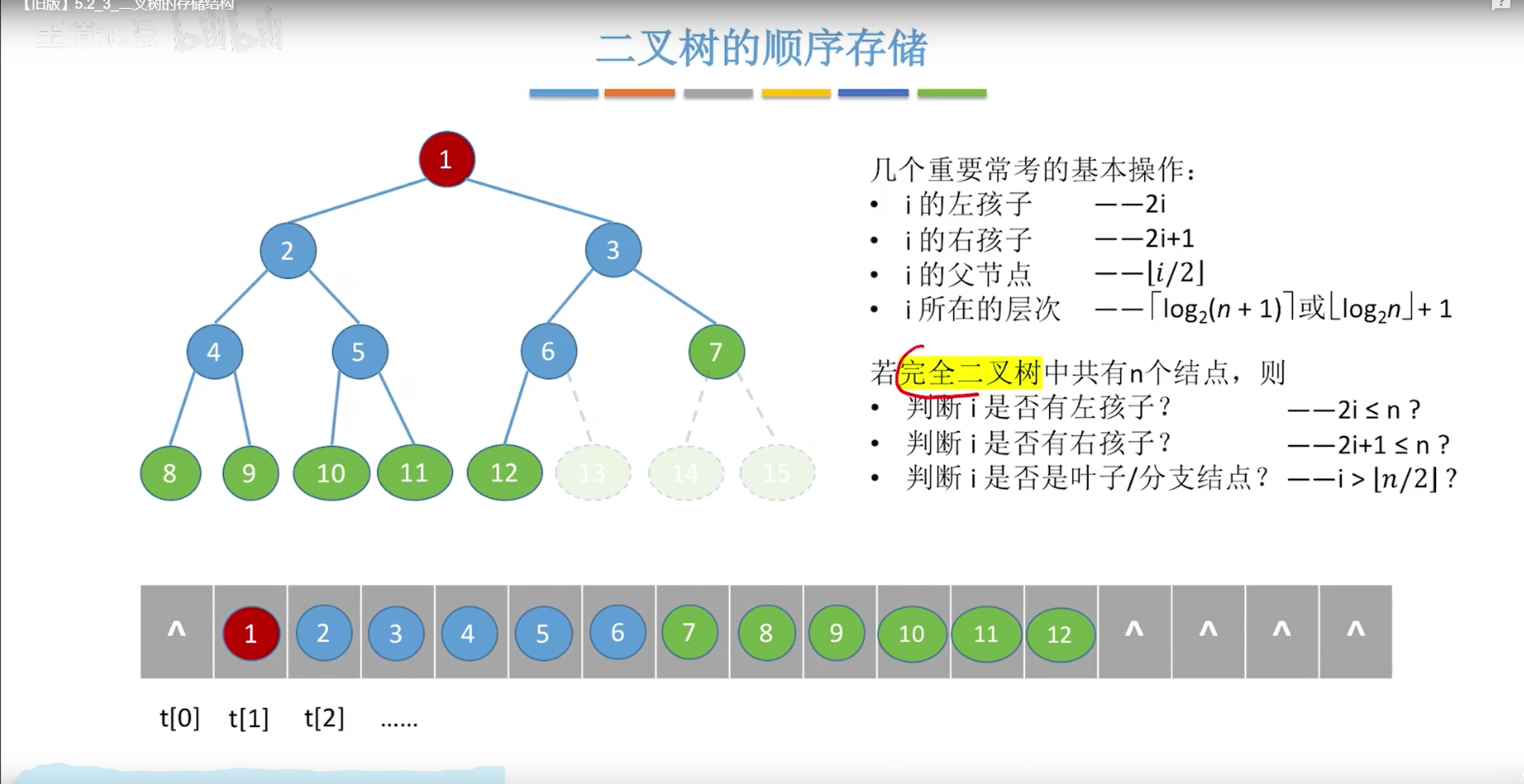
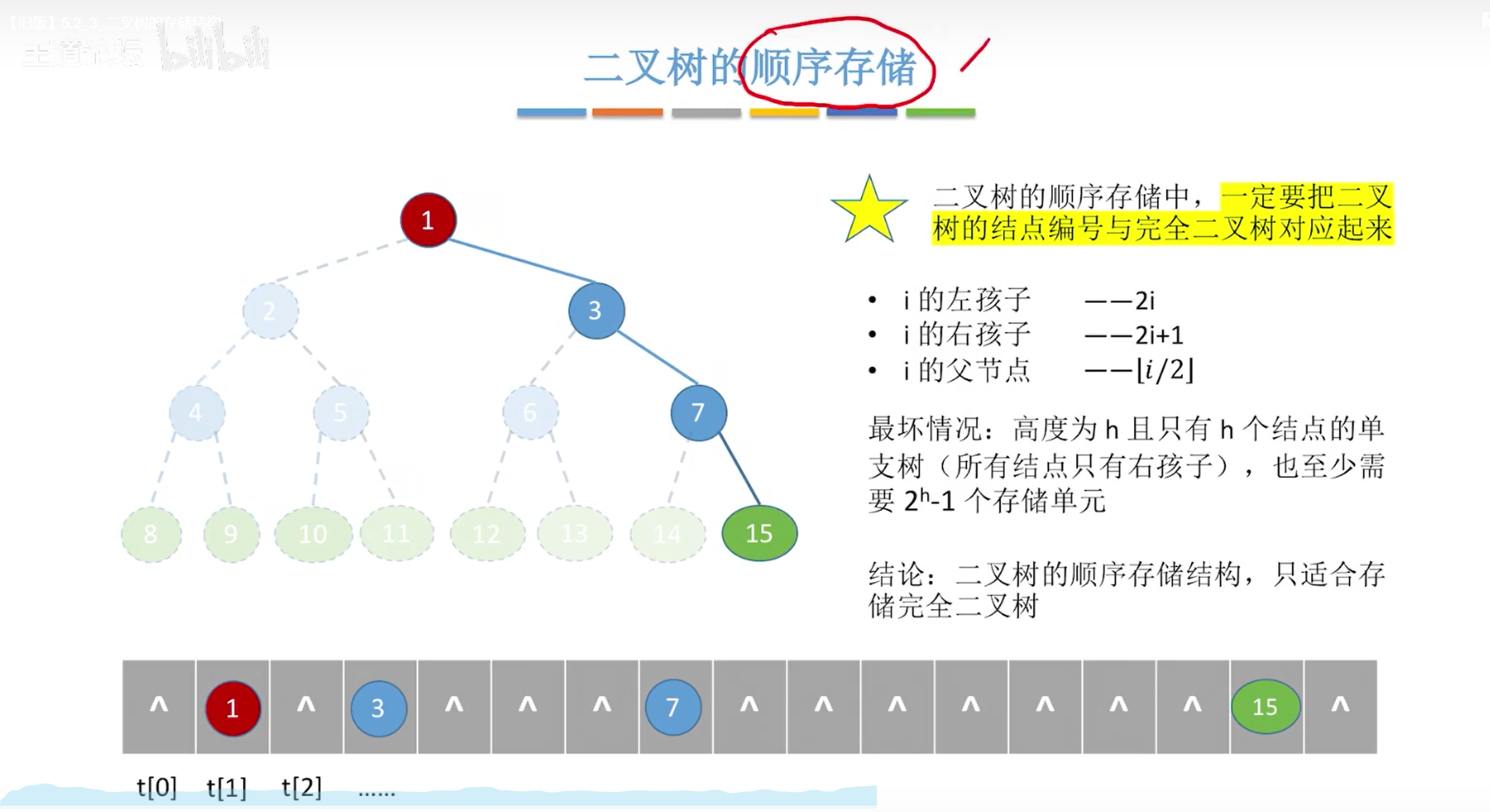
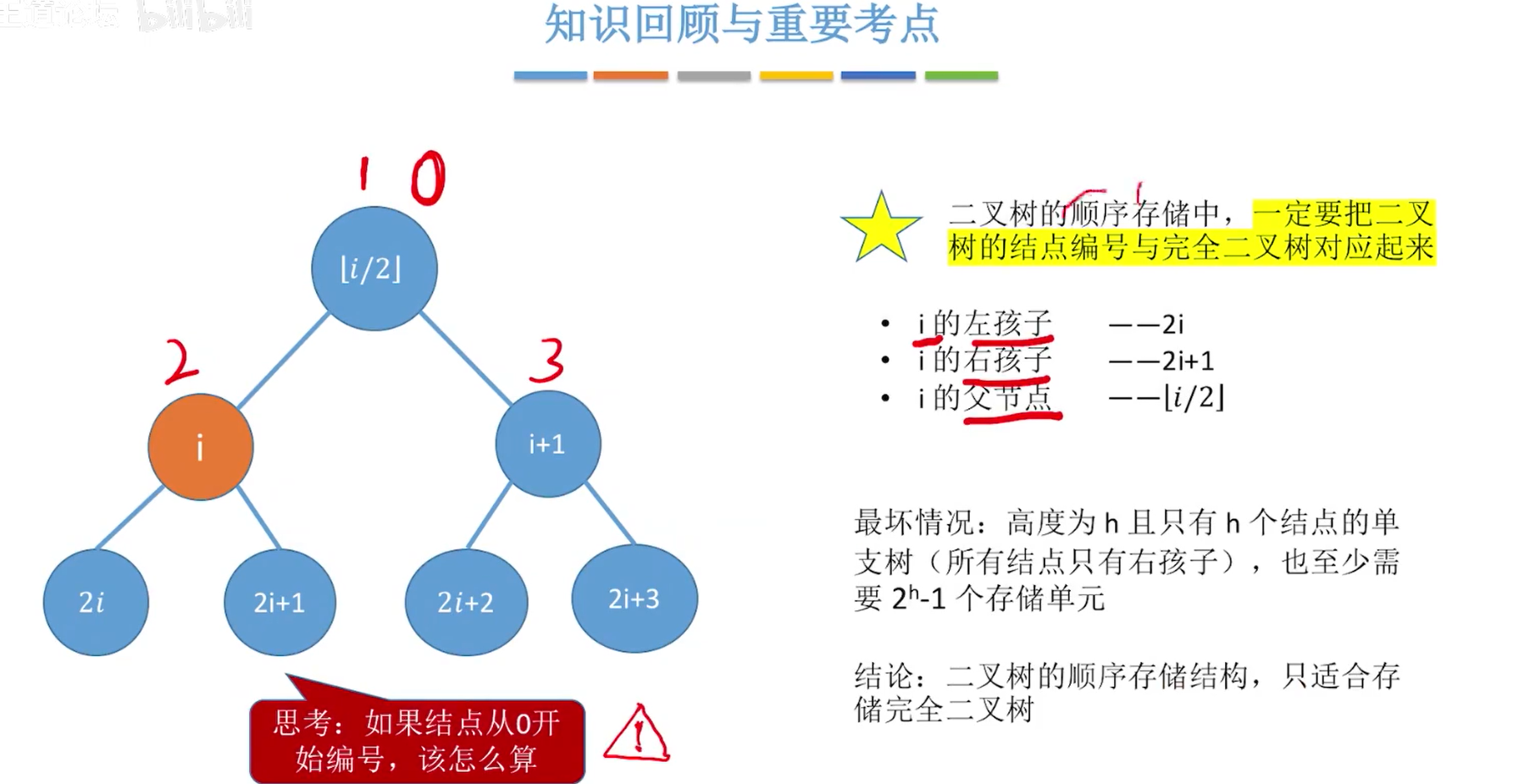
顺序存储

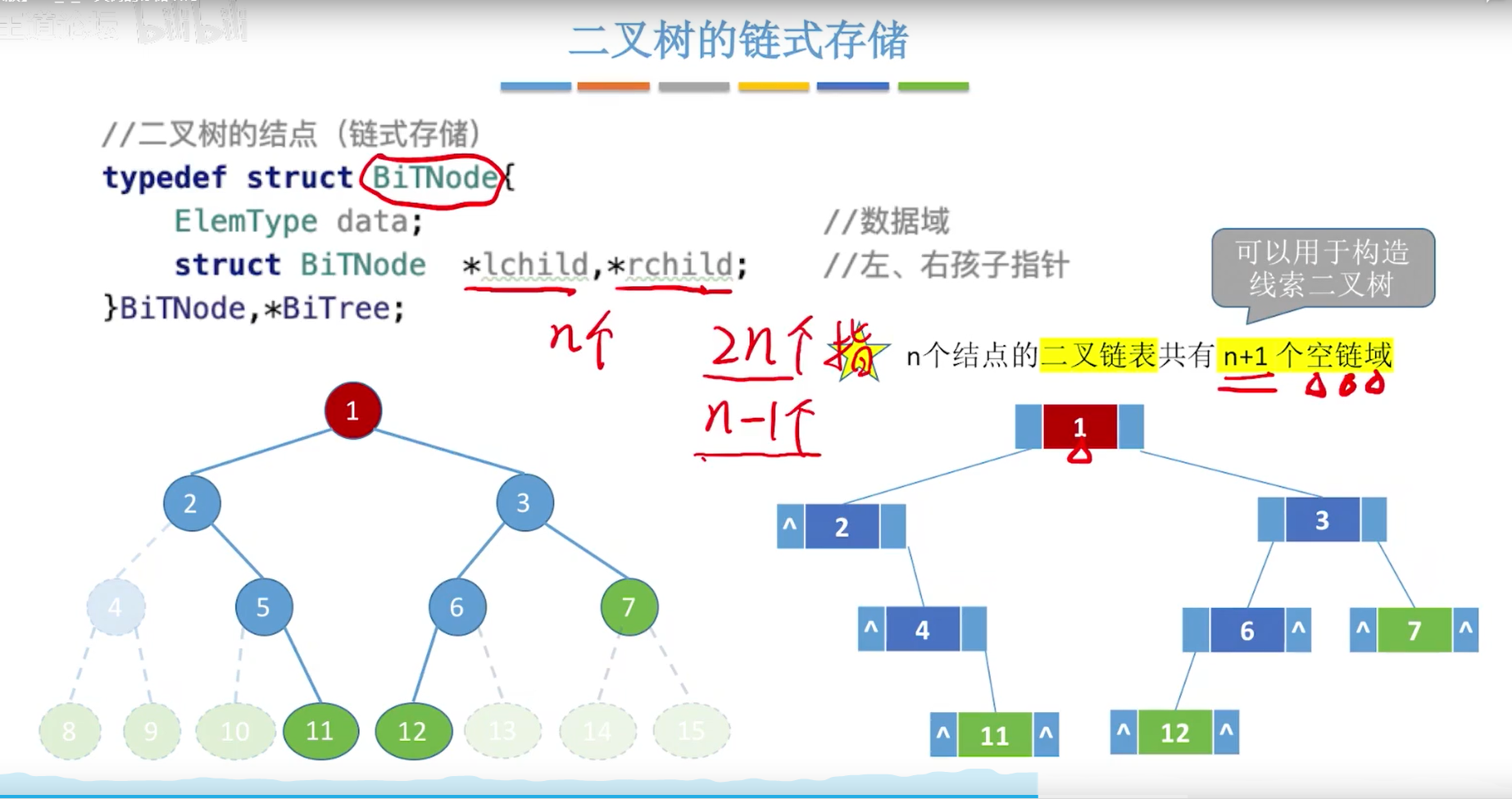
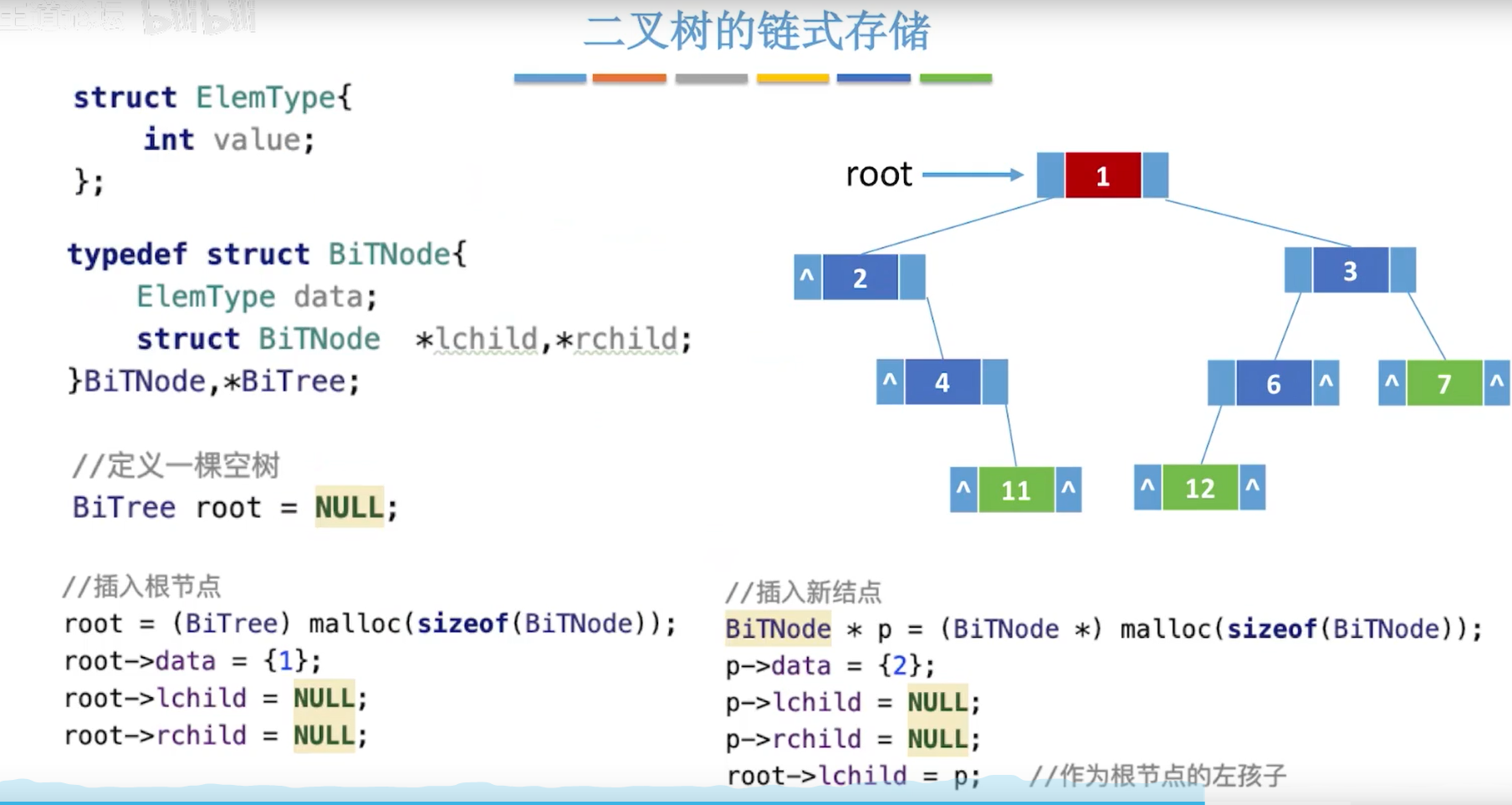
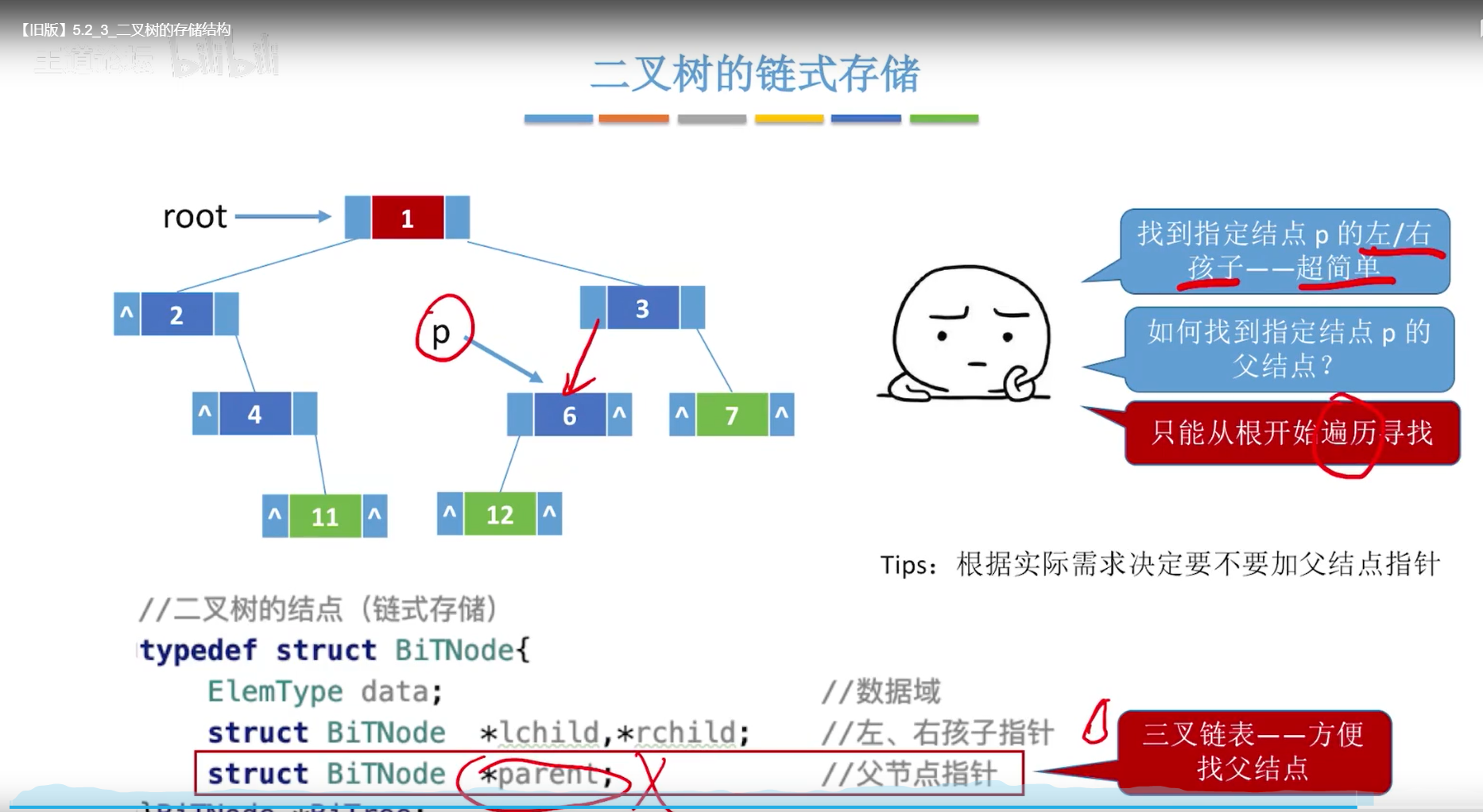
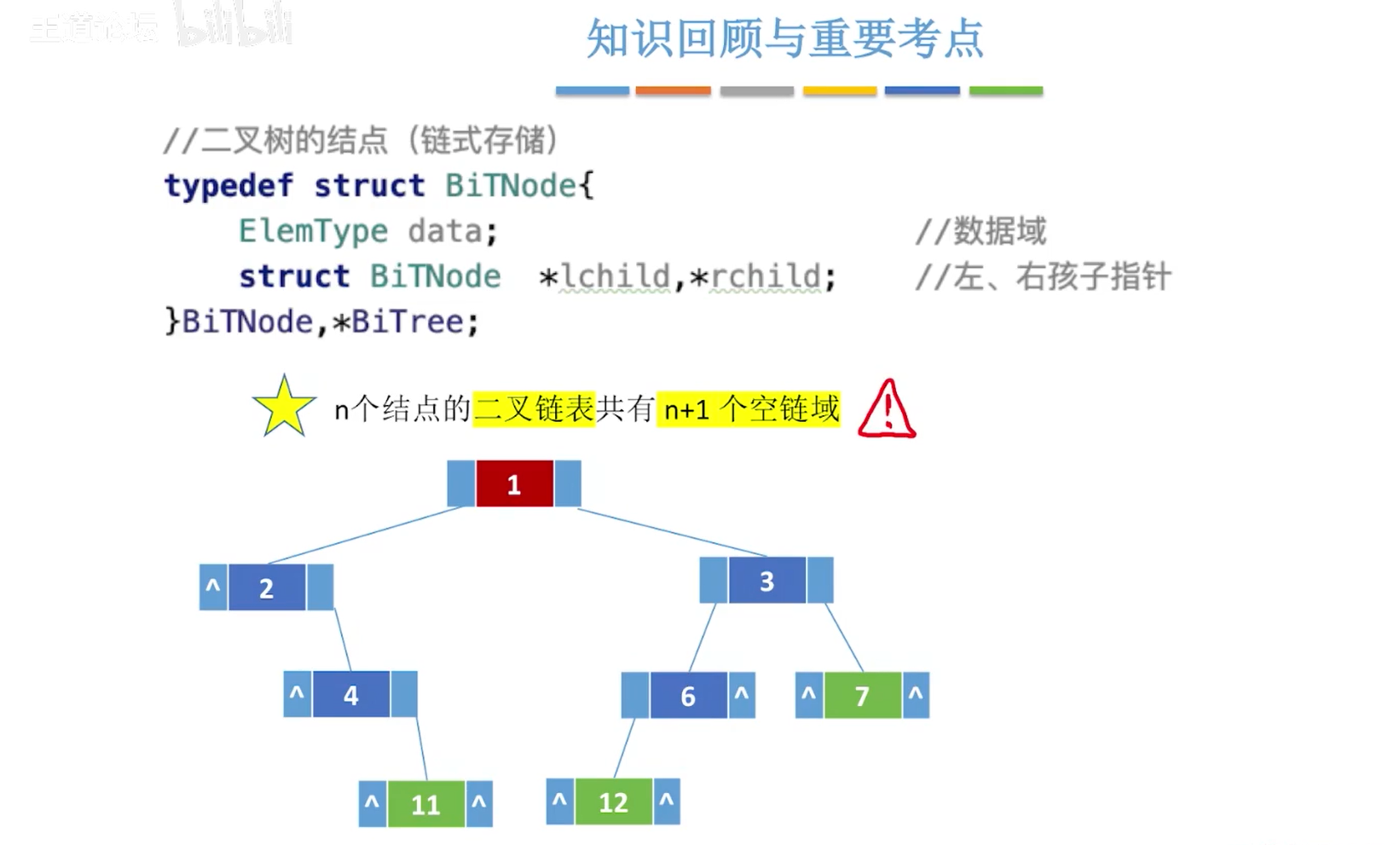
链式存储

小结

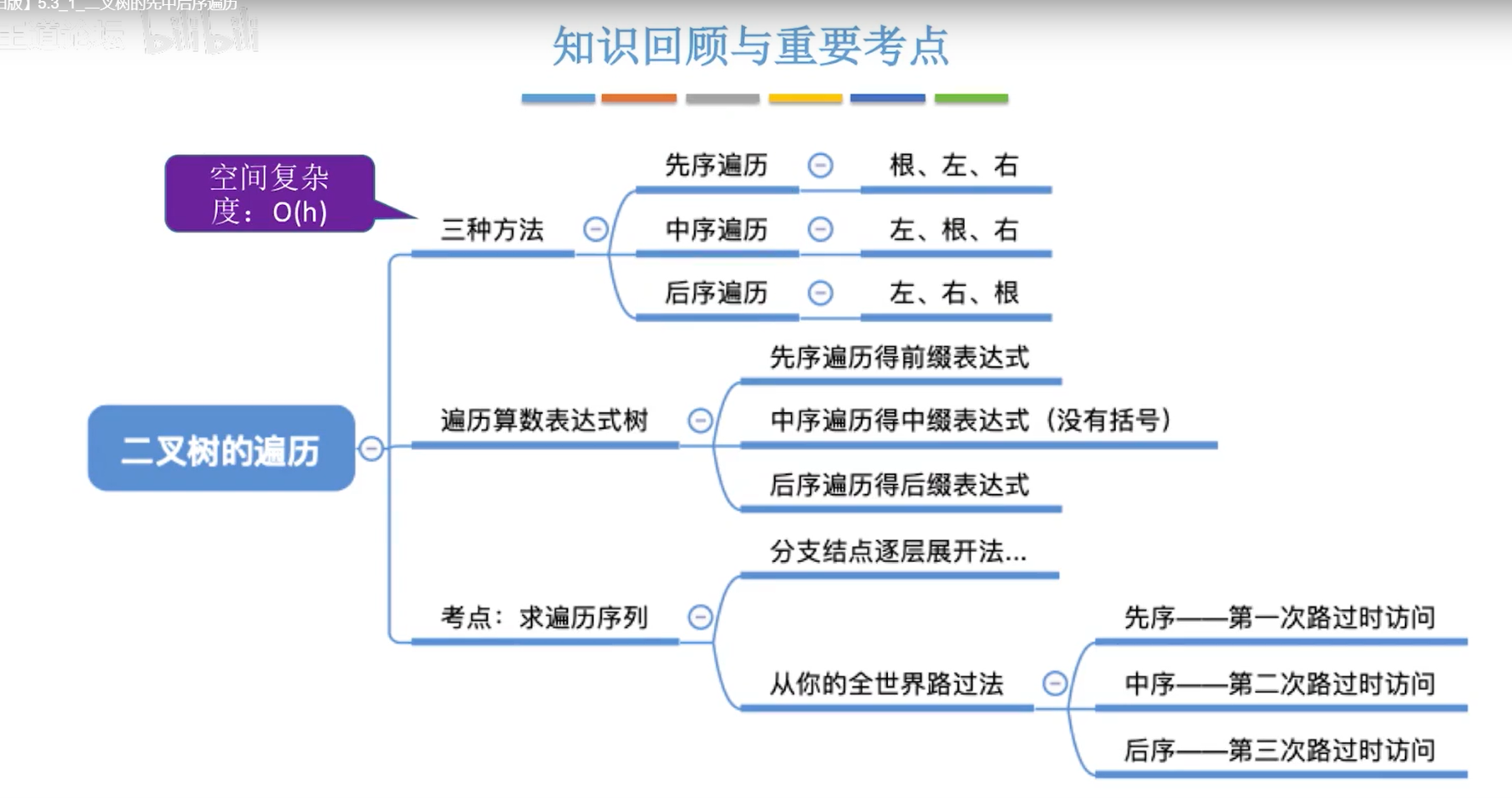
5.6二叉树的遍历

遍历：按照某个次序把所有节点都访问一次

先序遍历（NLR）:根左右

中序遍历（LNR）:左根右

后序遍历（LRN）:左右根

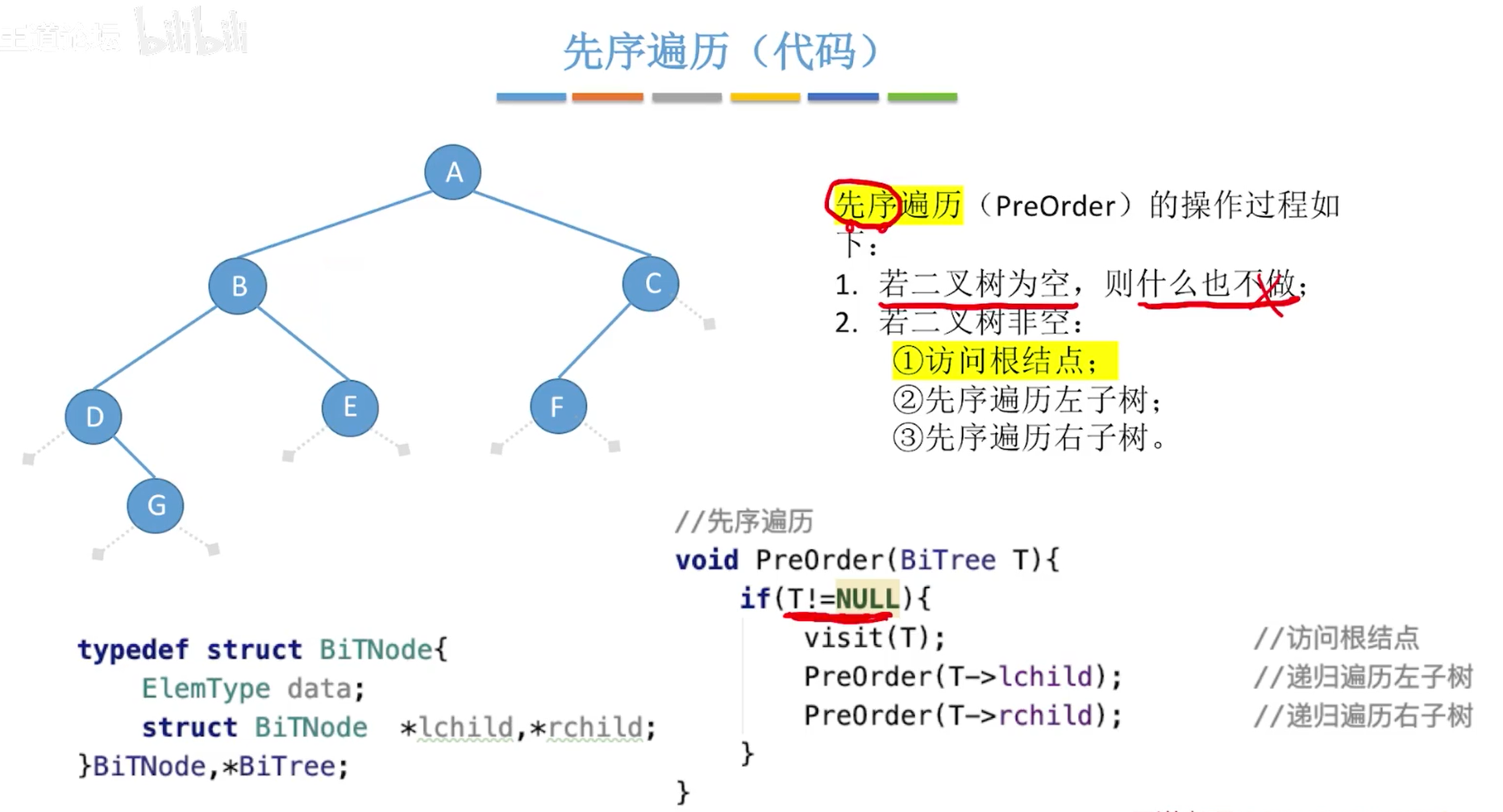
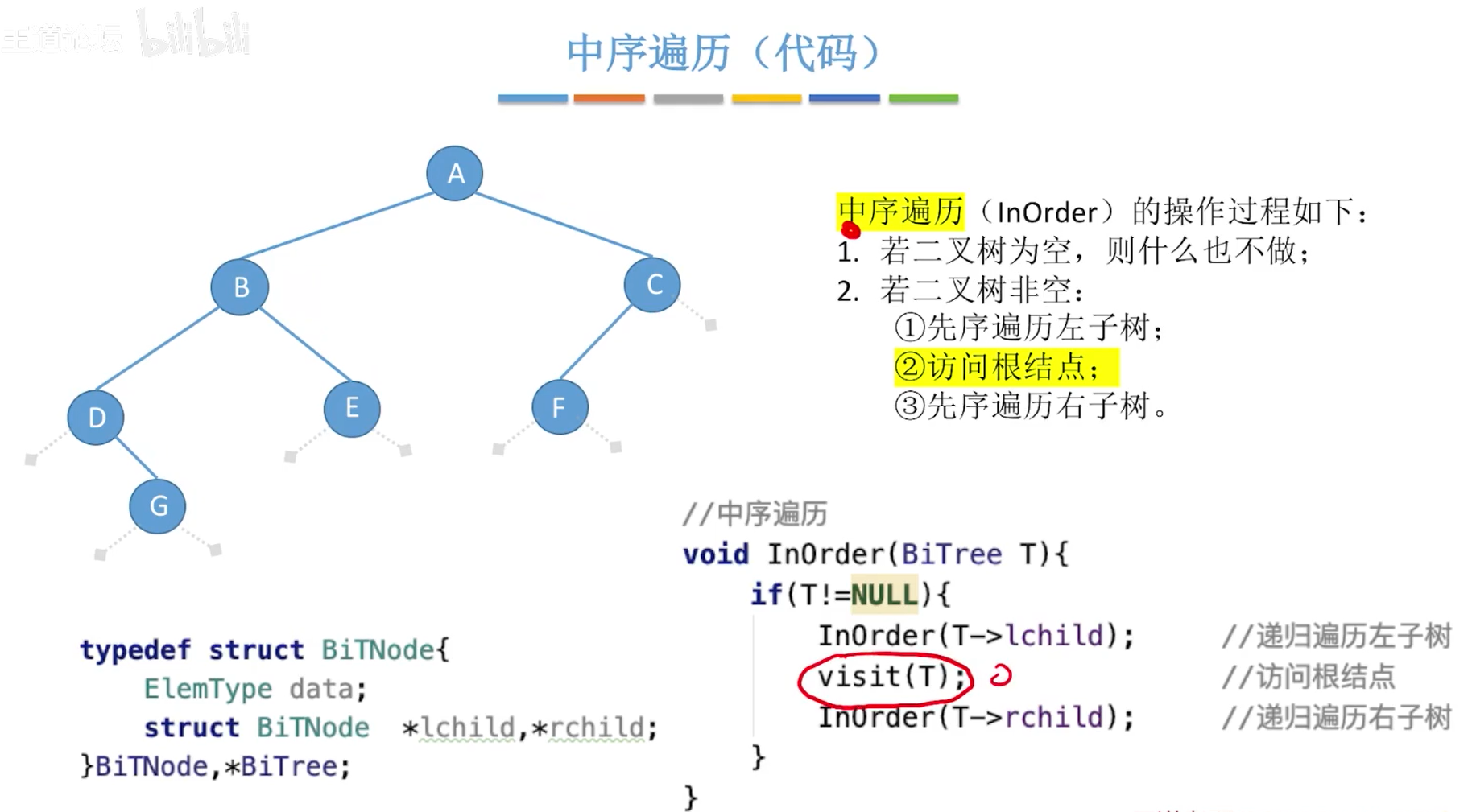
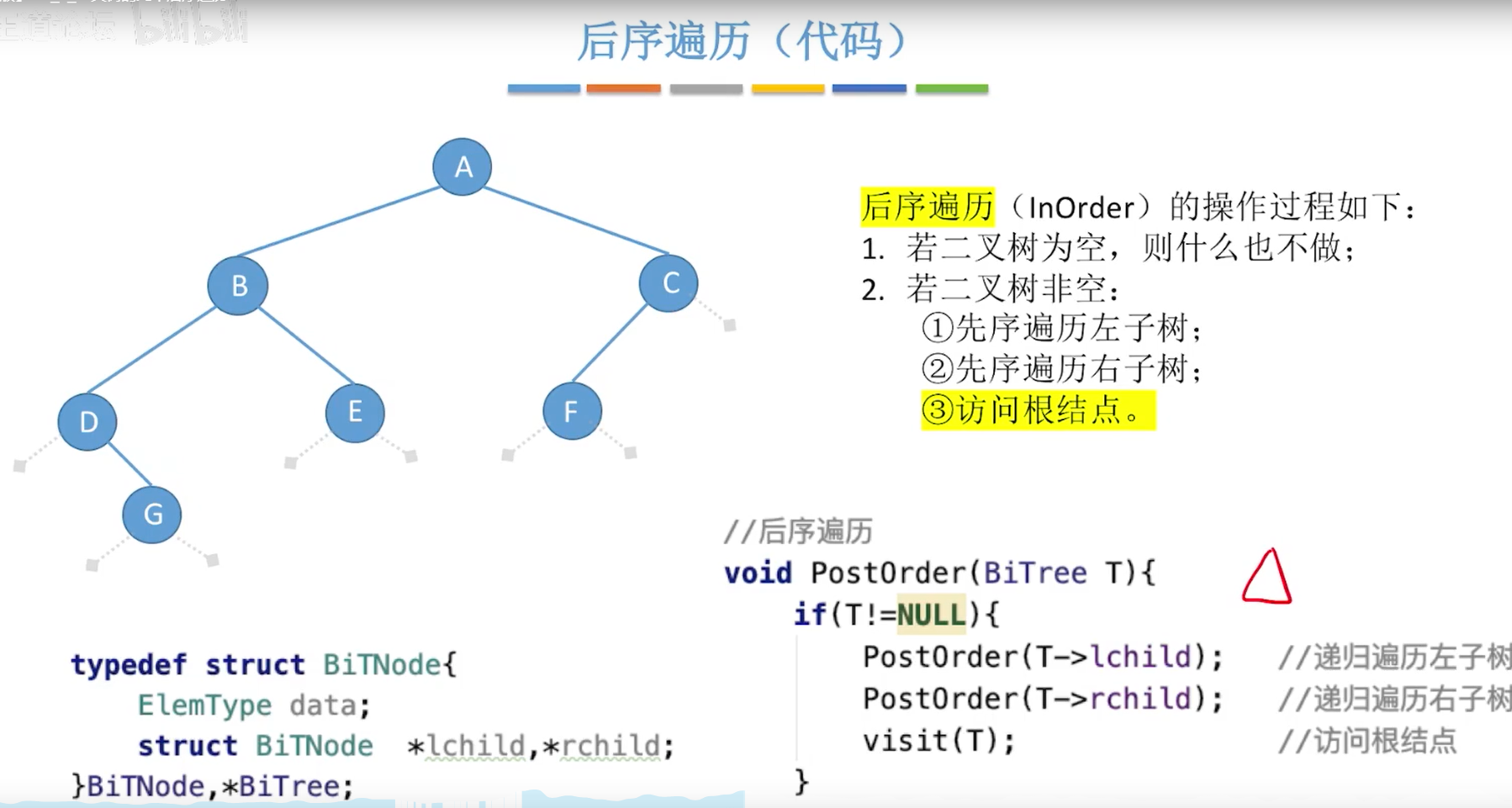
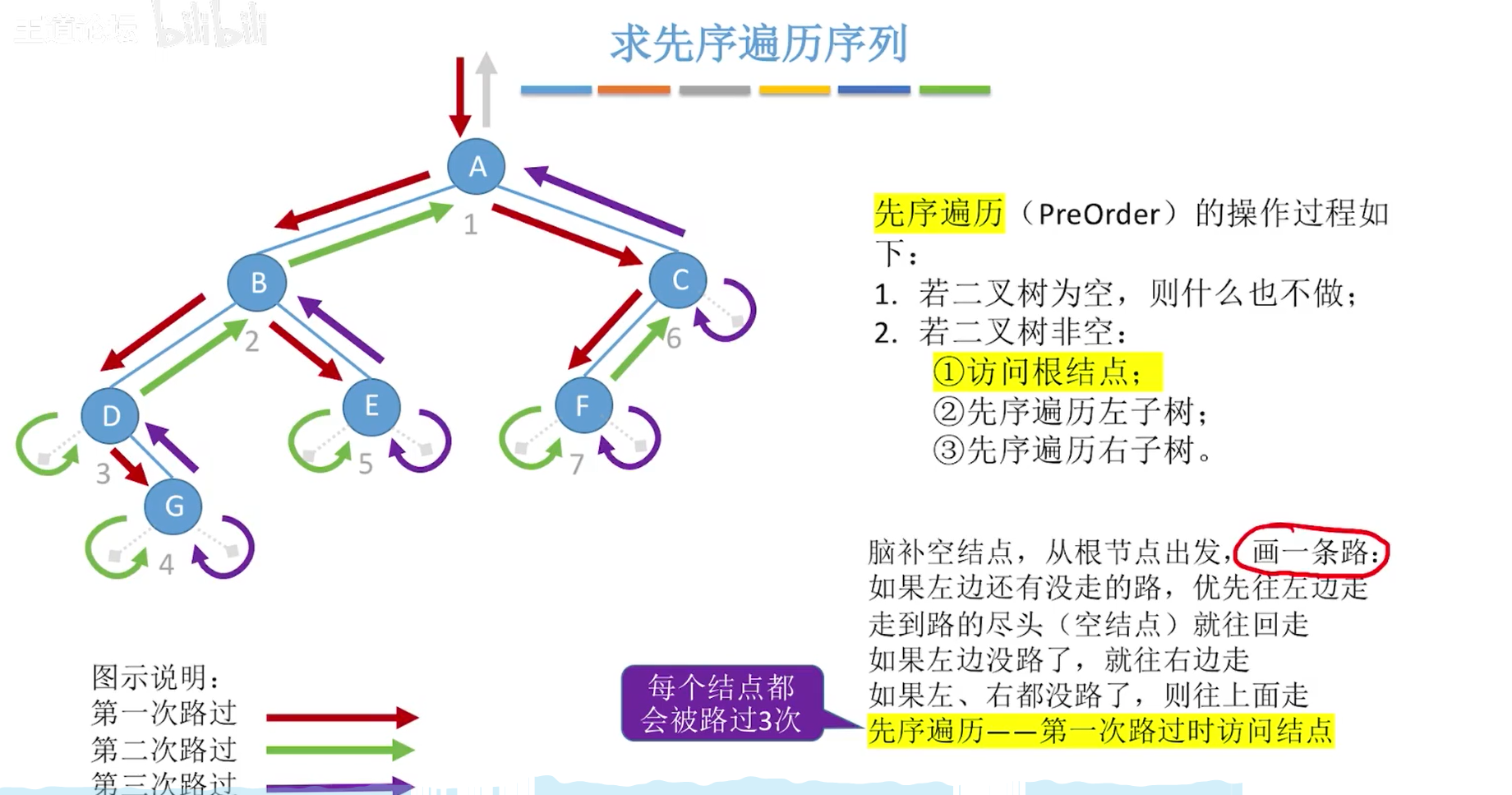
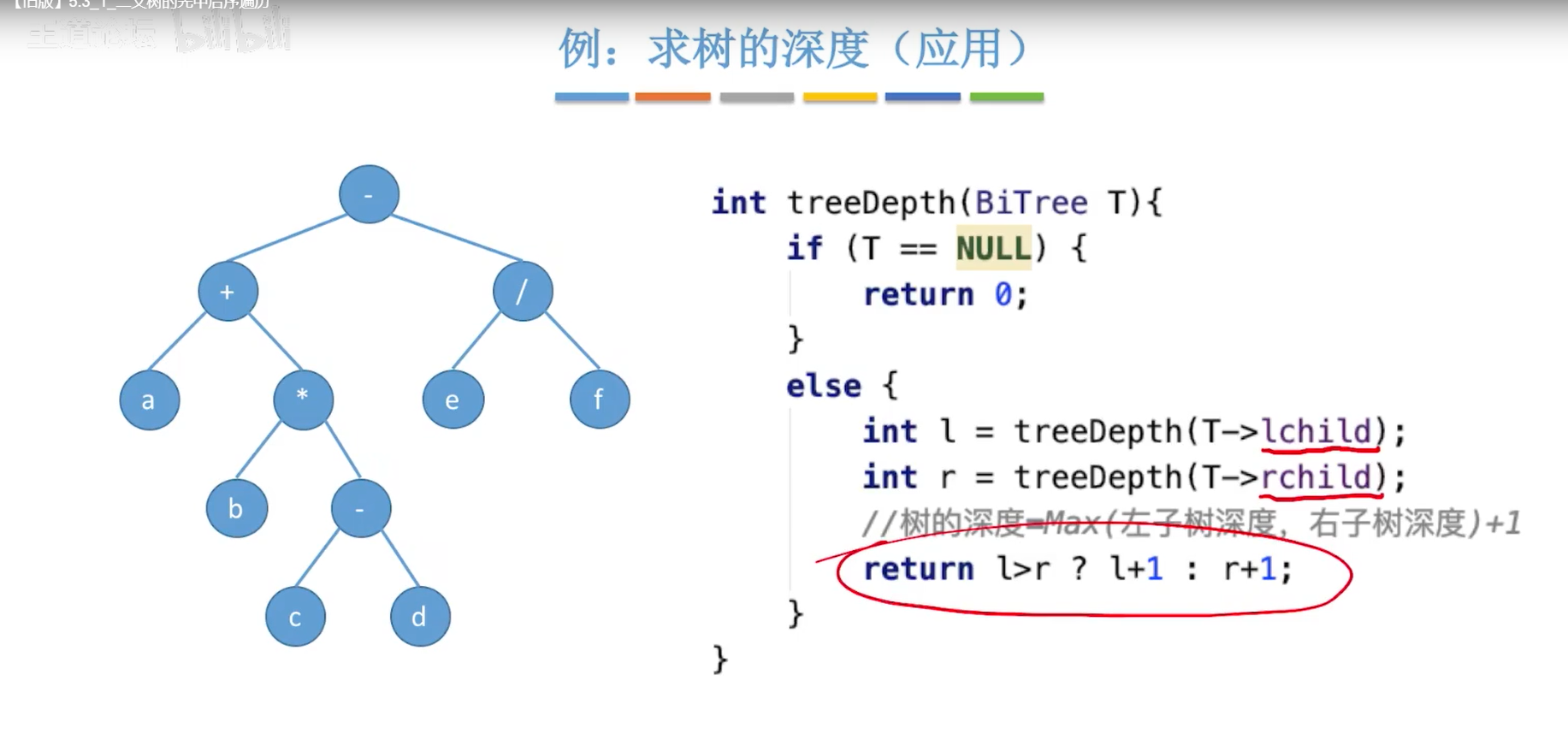
小结

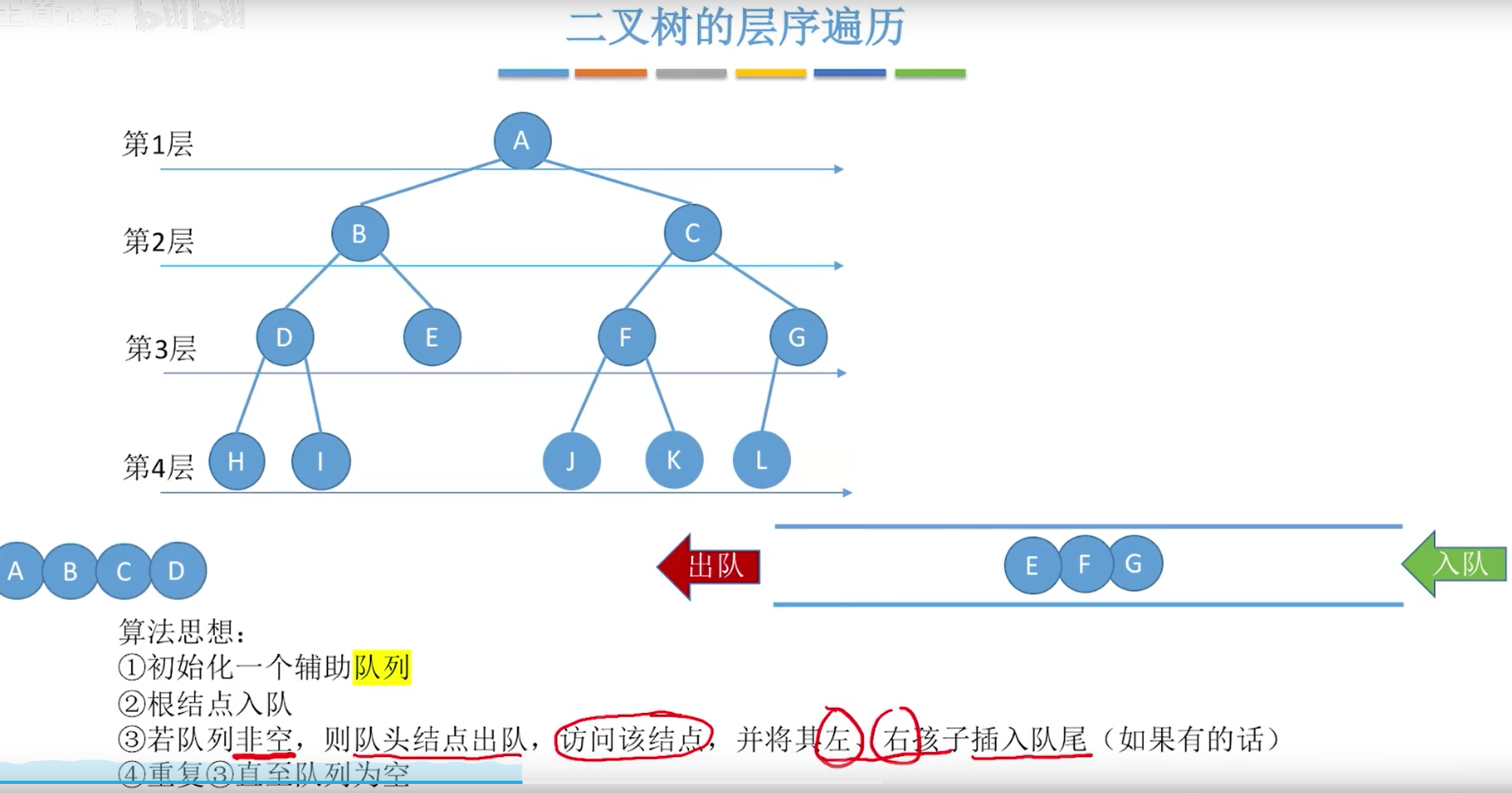
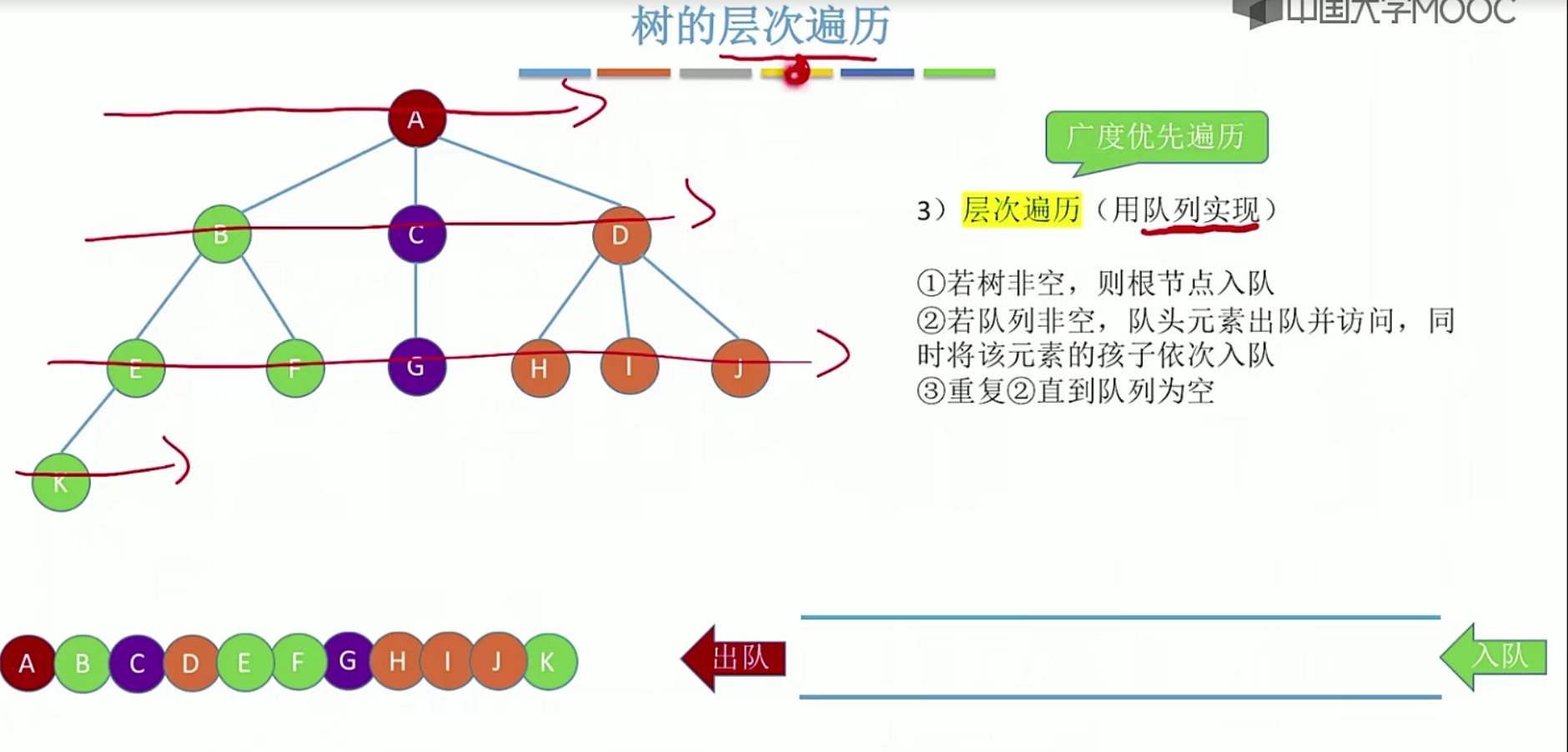
5.7二叉树的层序遍历

小结

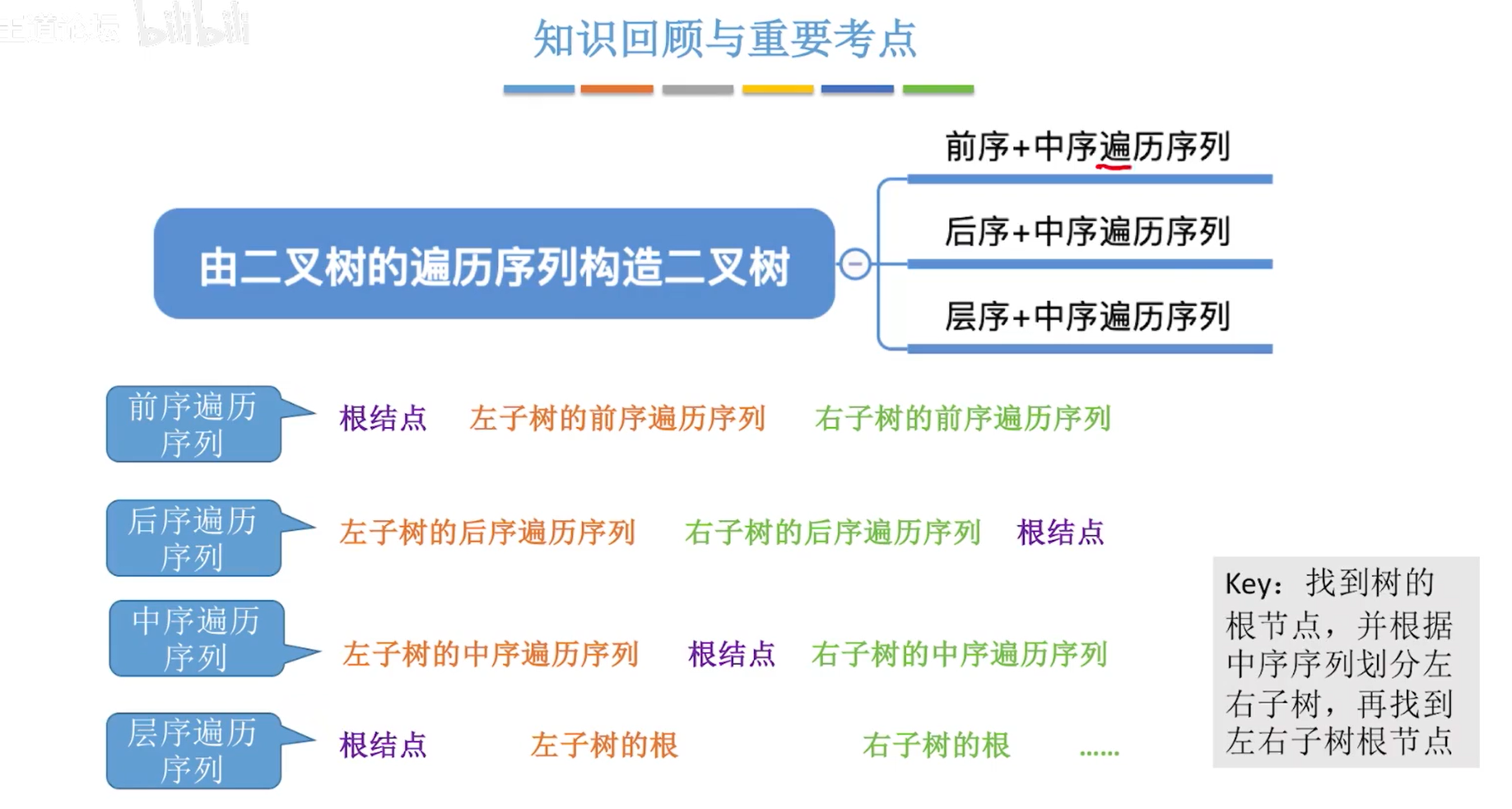
5.8由遍历序列构造二叉树


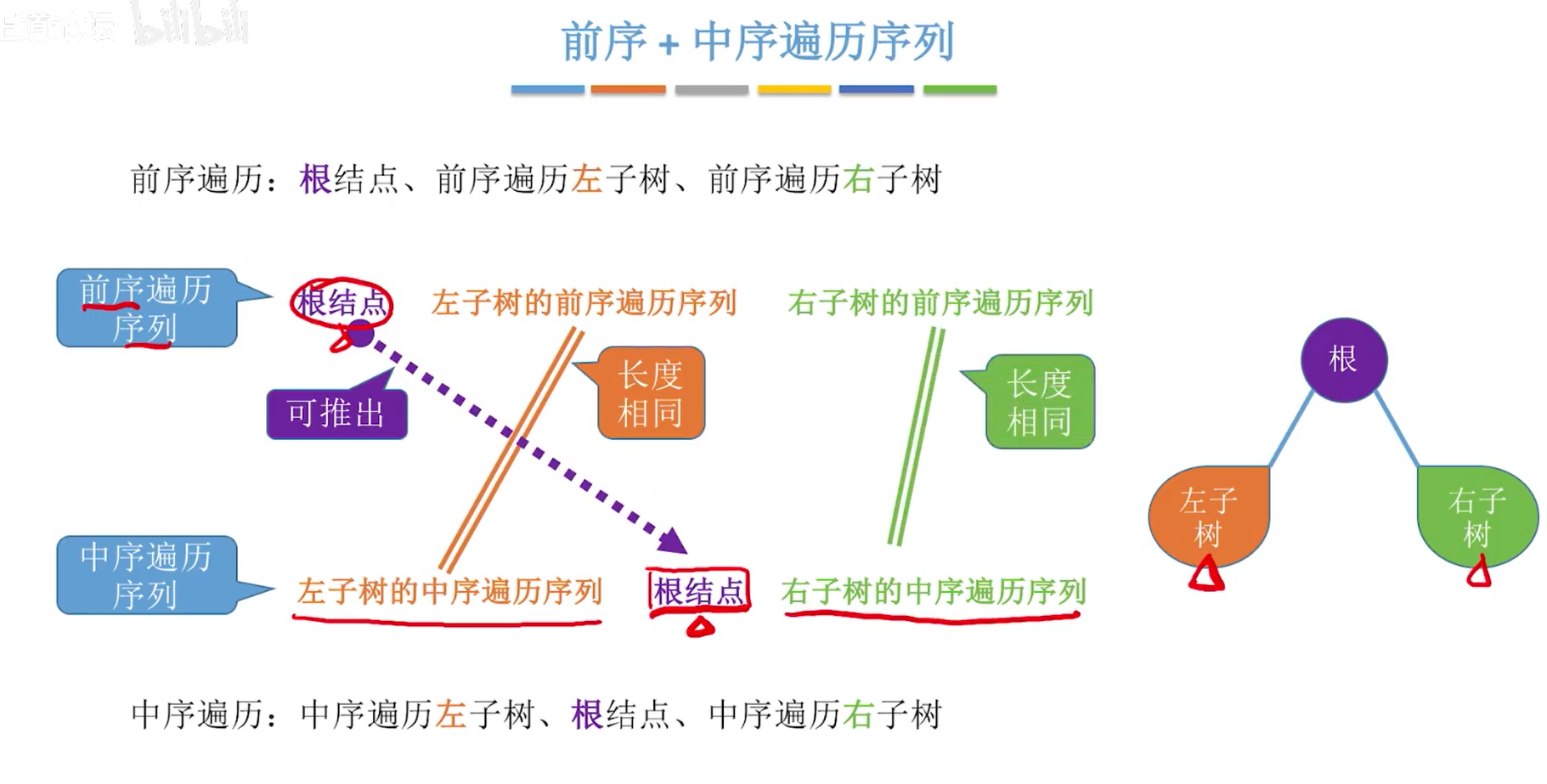
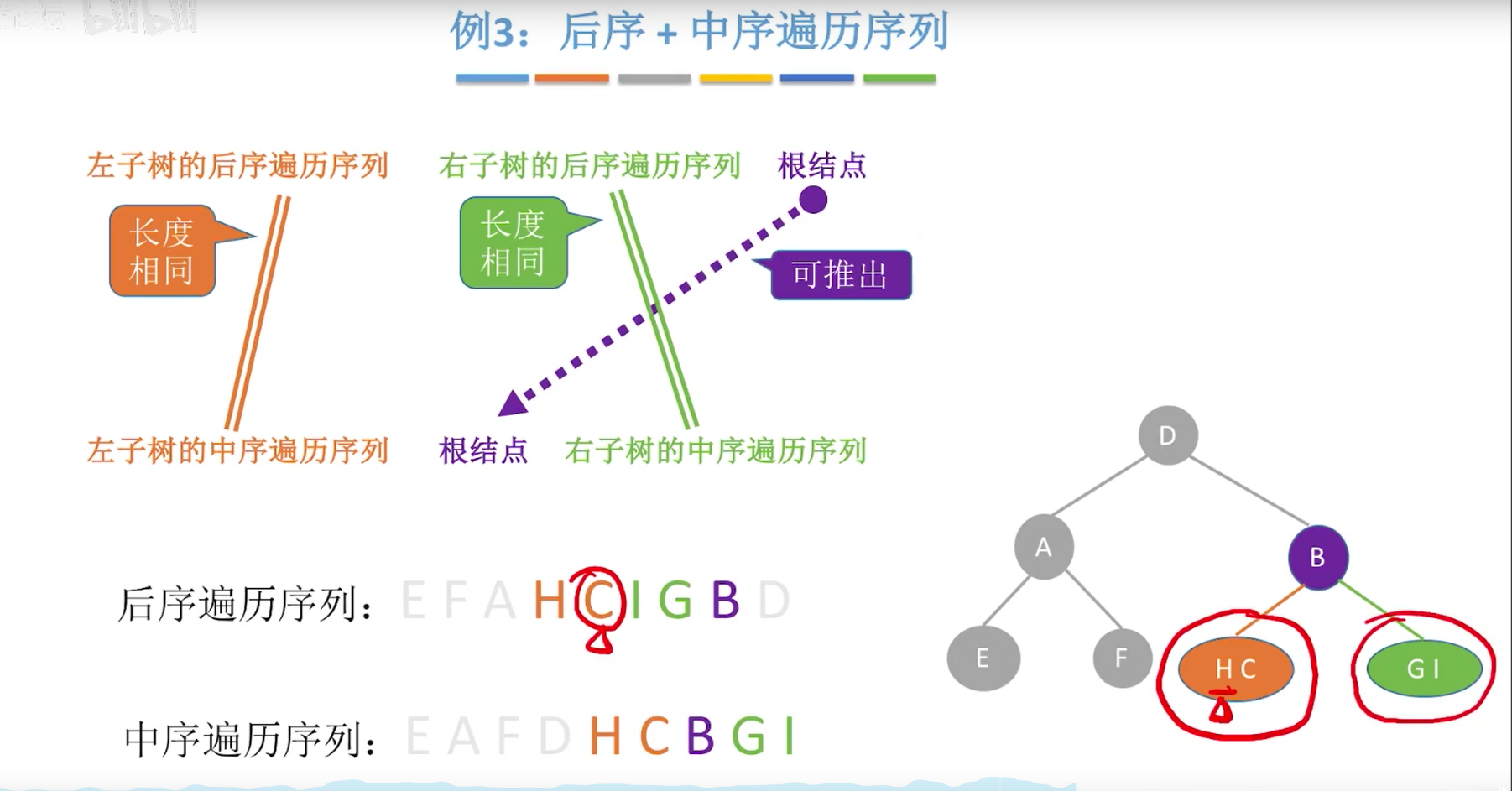
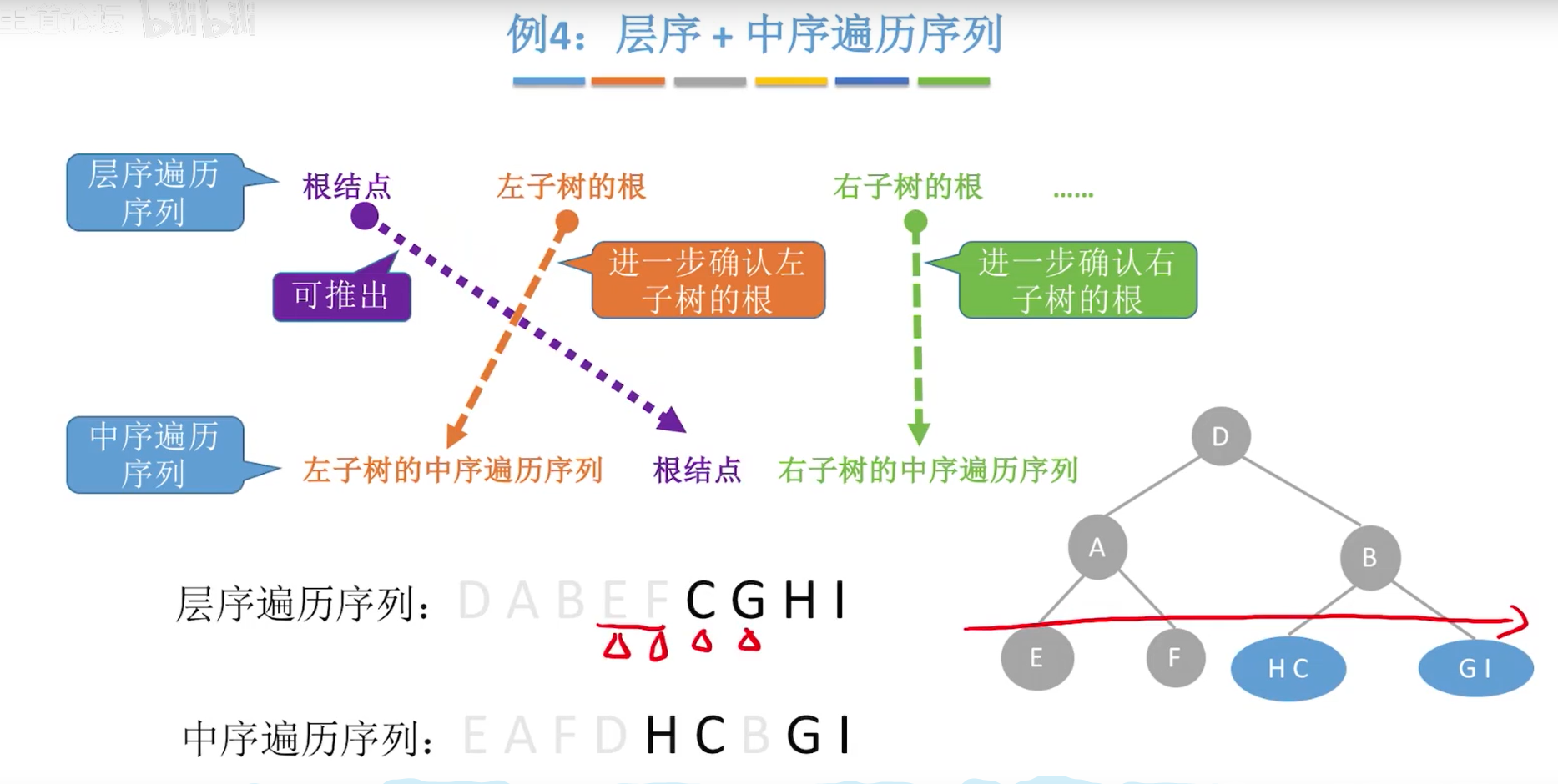
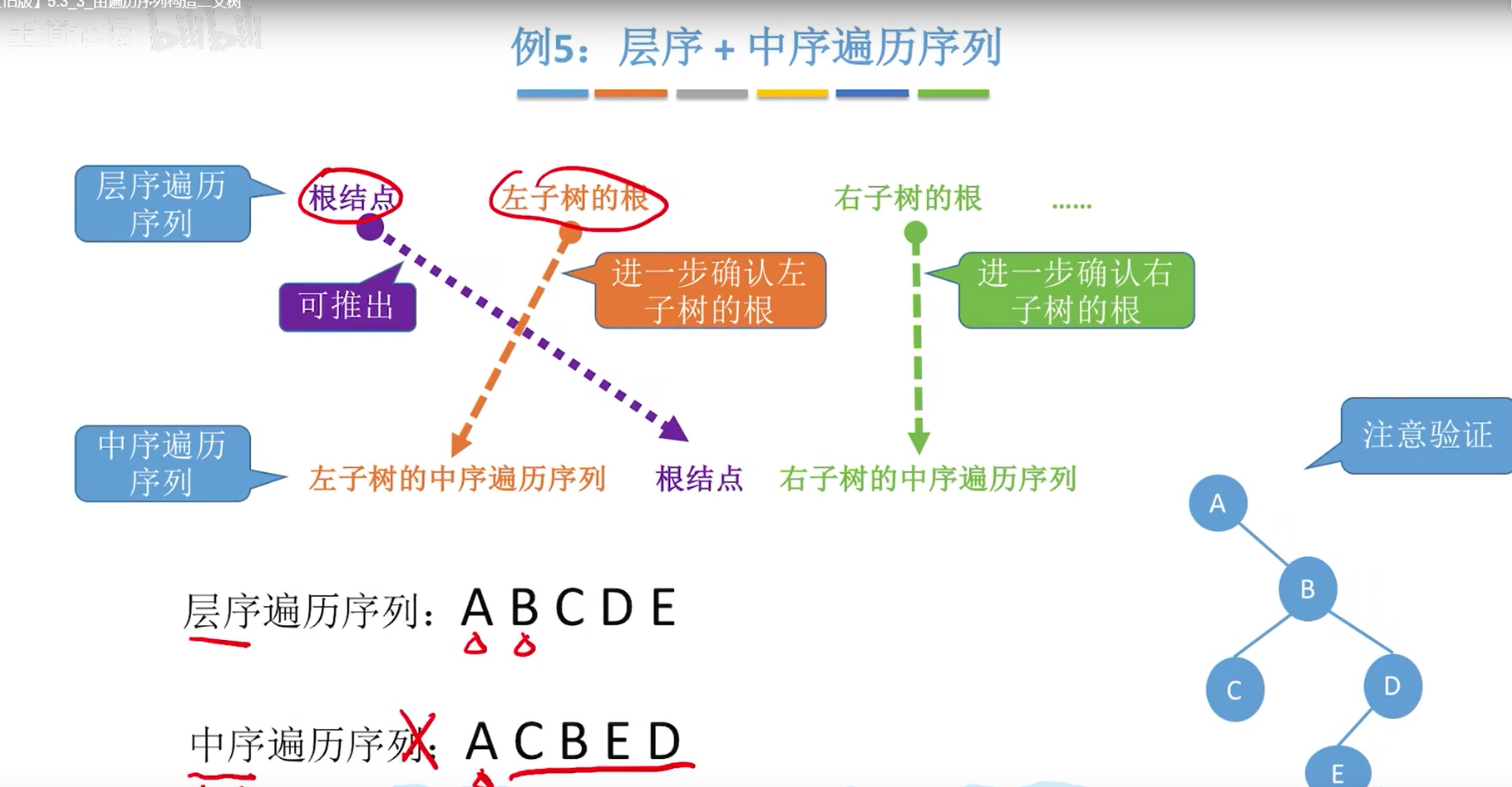
小结

5.9线索二叉树

5.9.1线索二叉树的引出（作用）

中序线索二叉树


线索二叉树的存储结构


具体表现


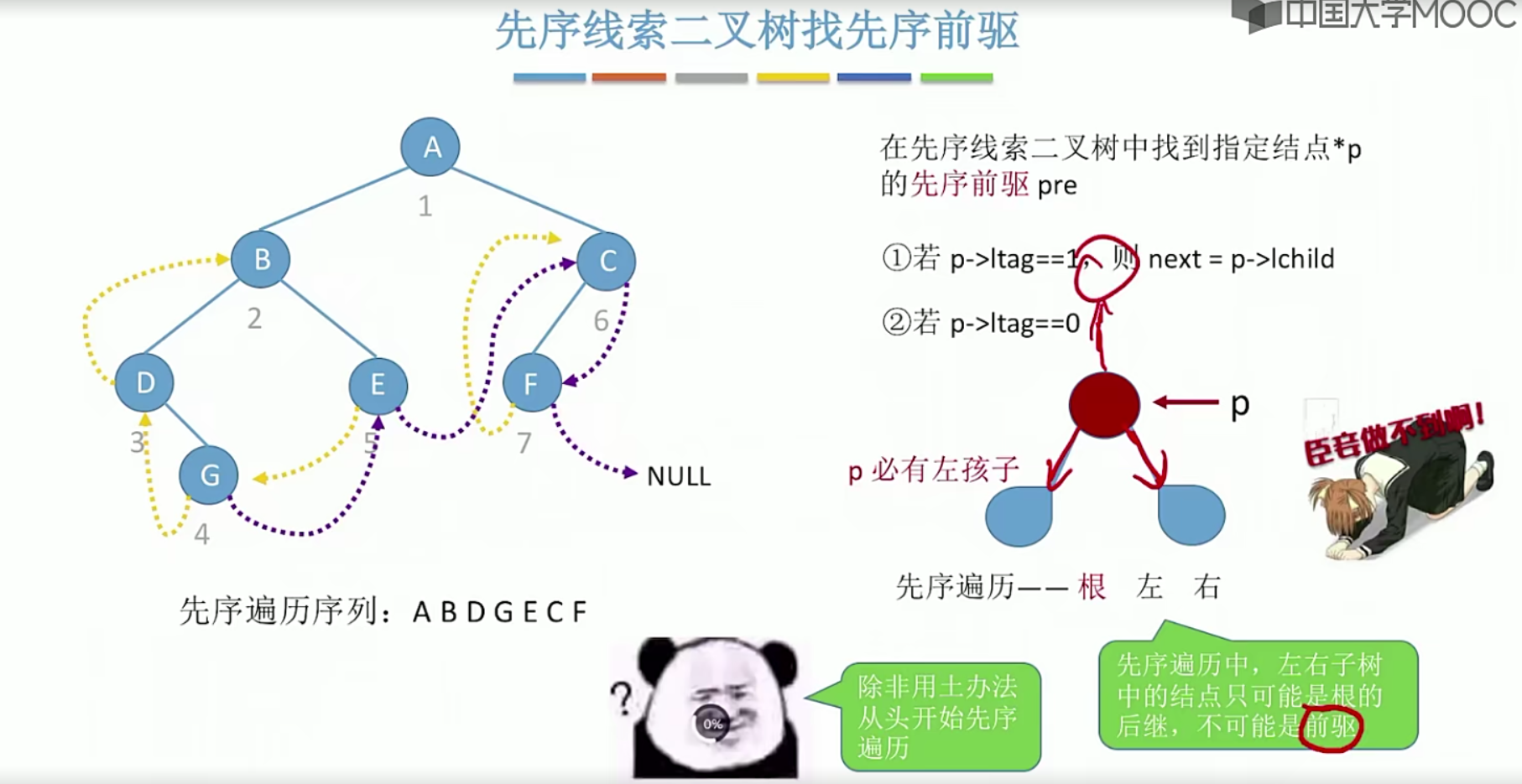
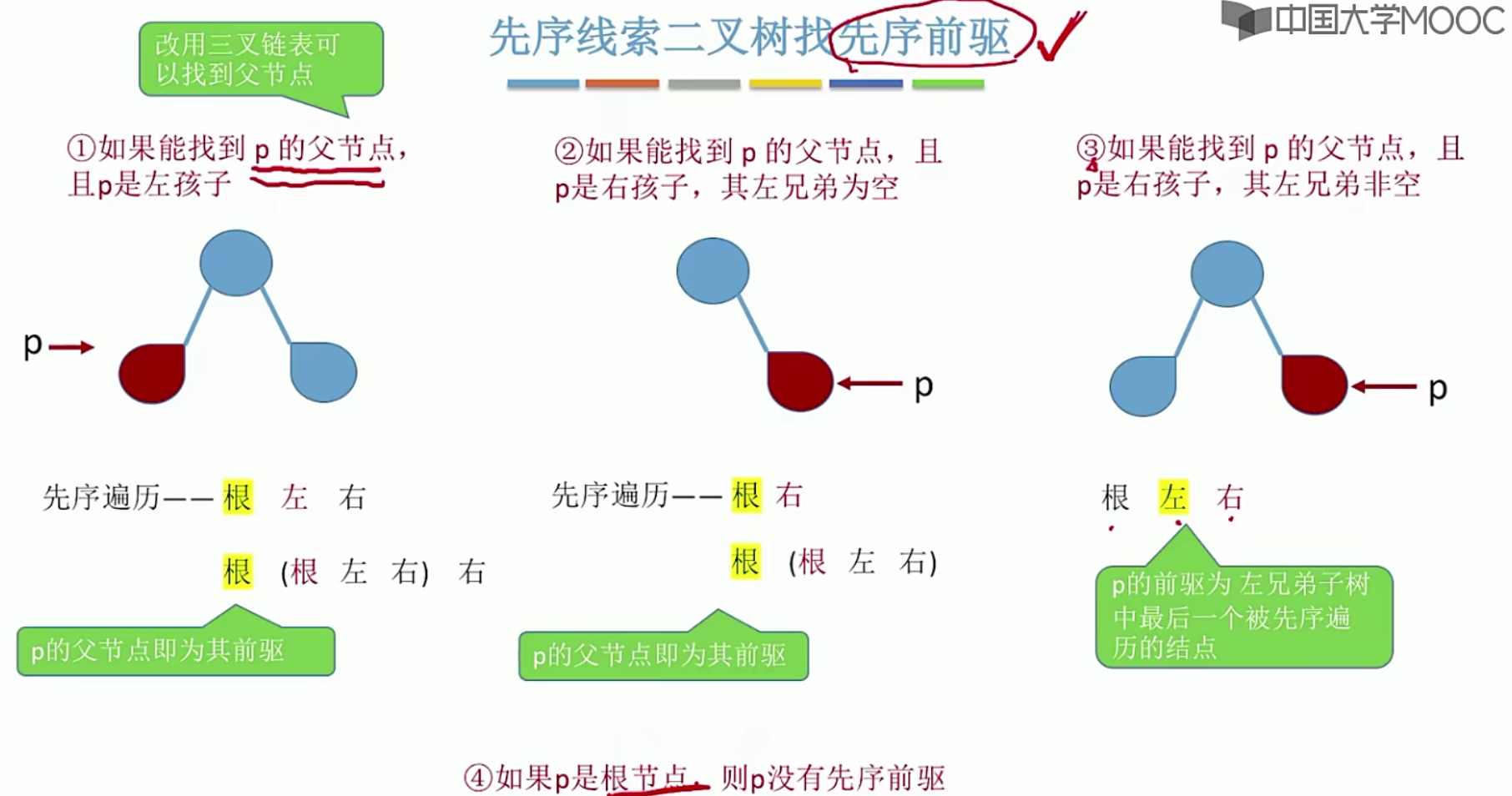
先序线索二叉树



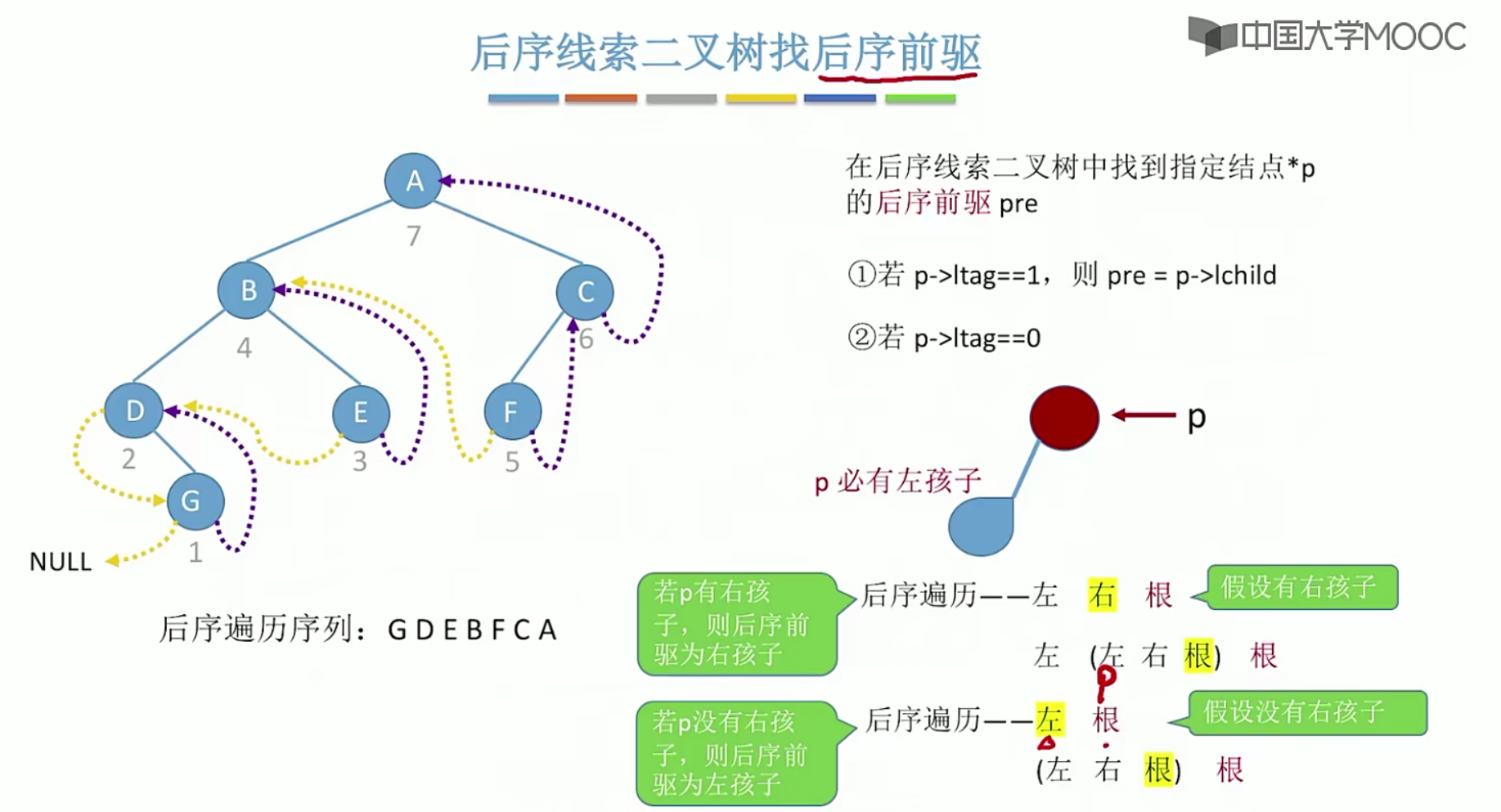
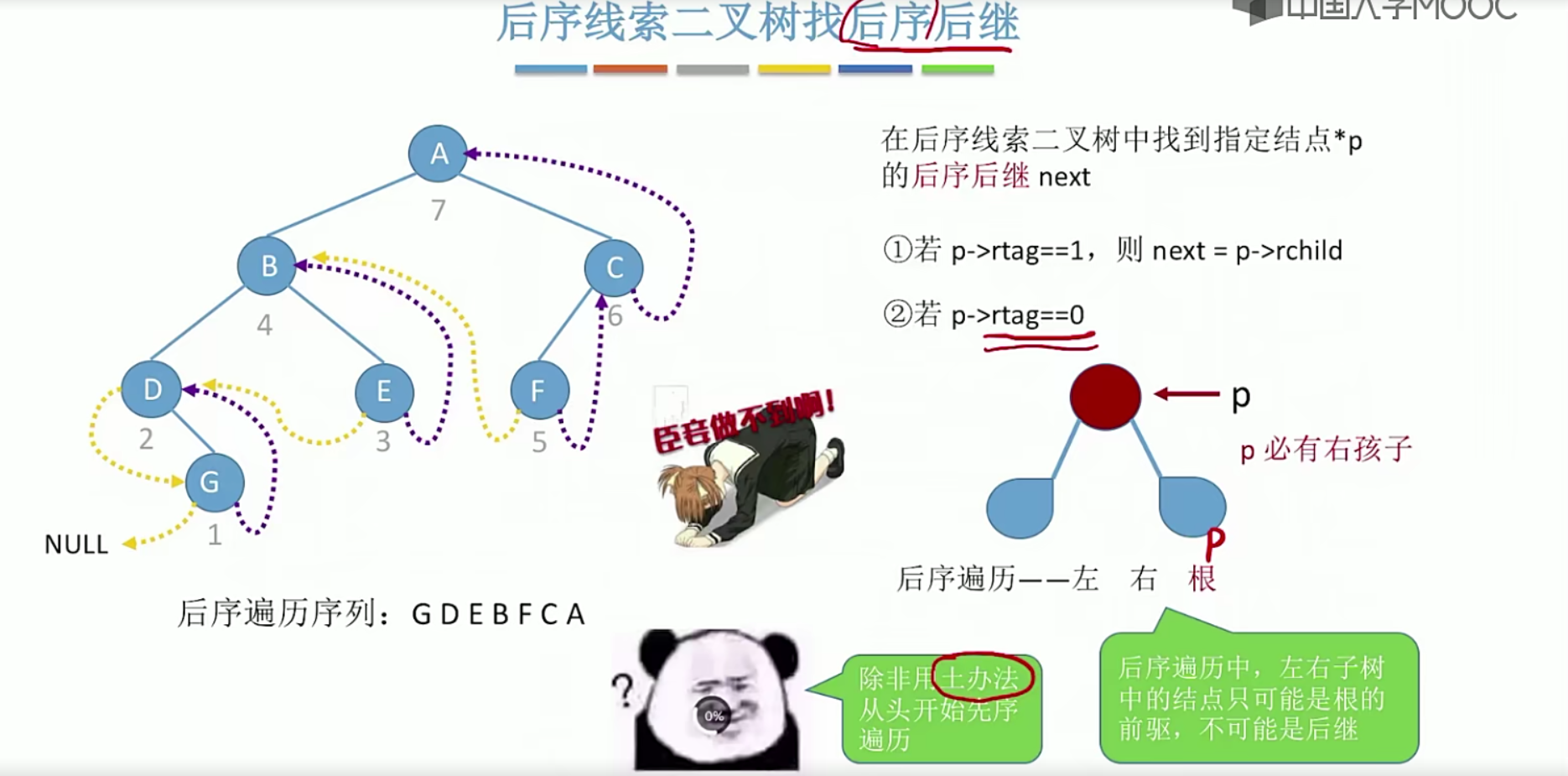
后序线索二叉树



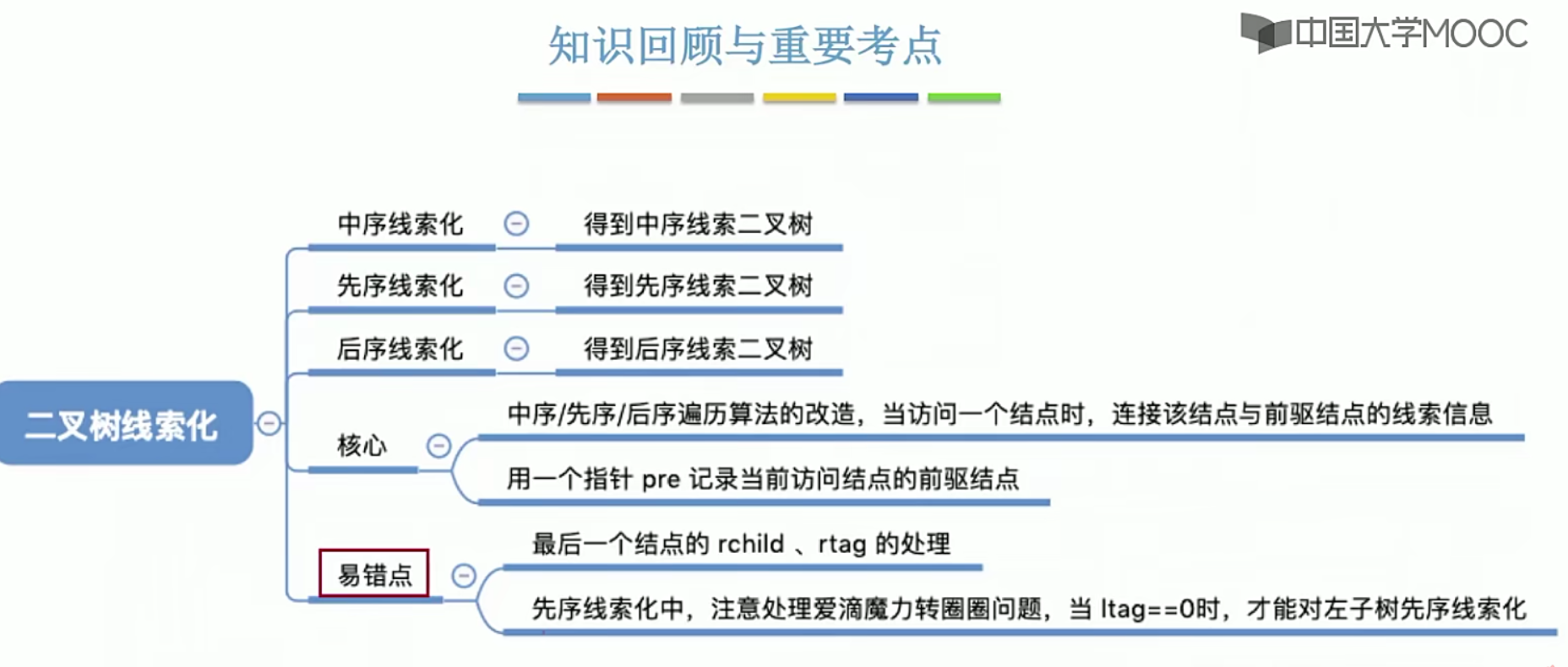
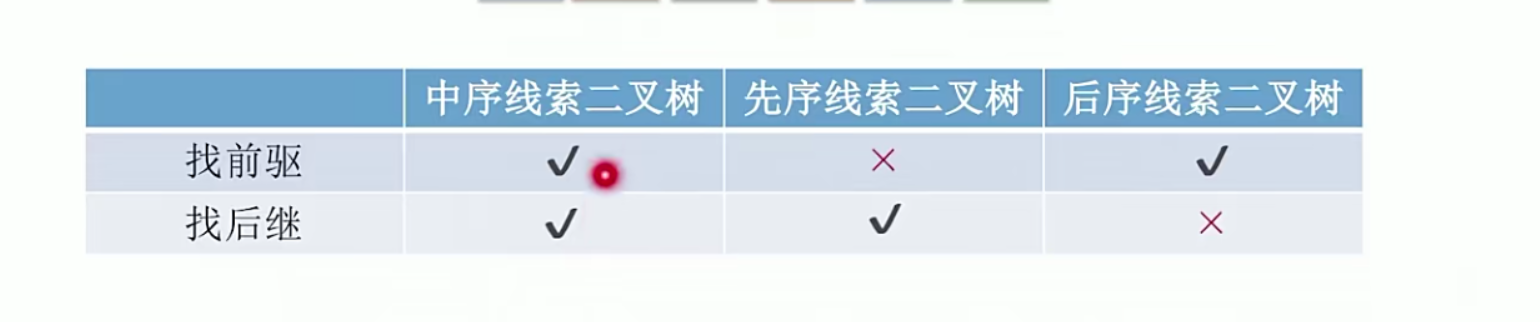
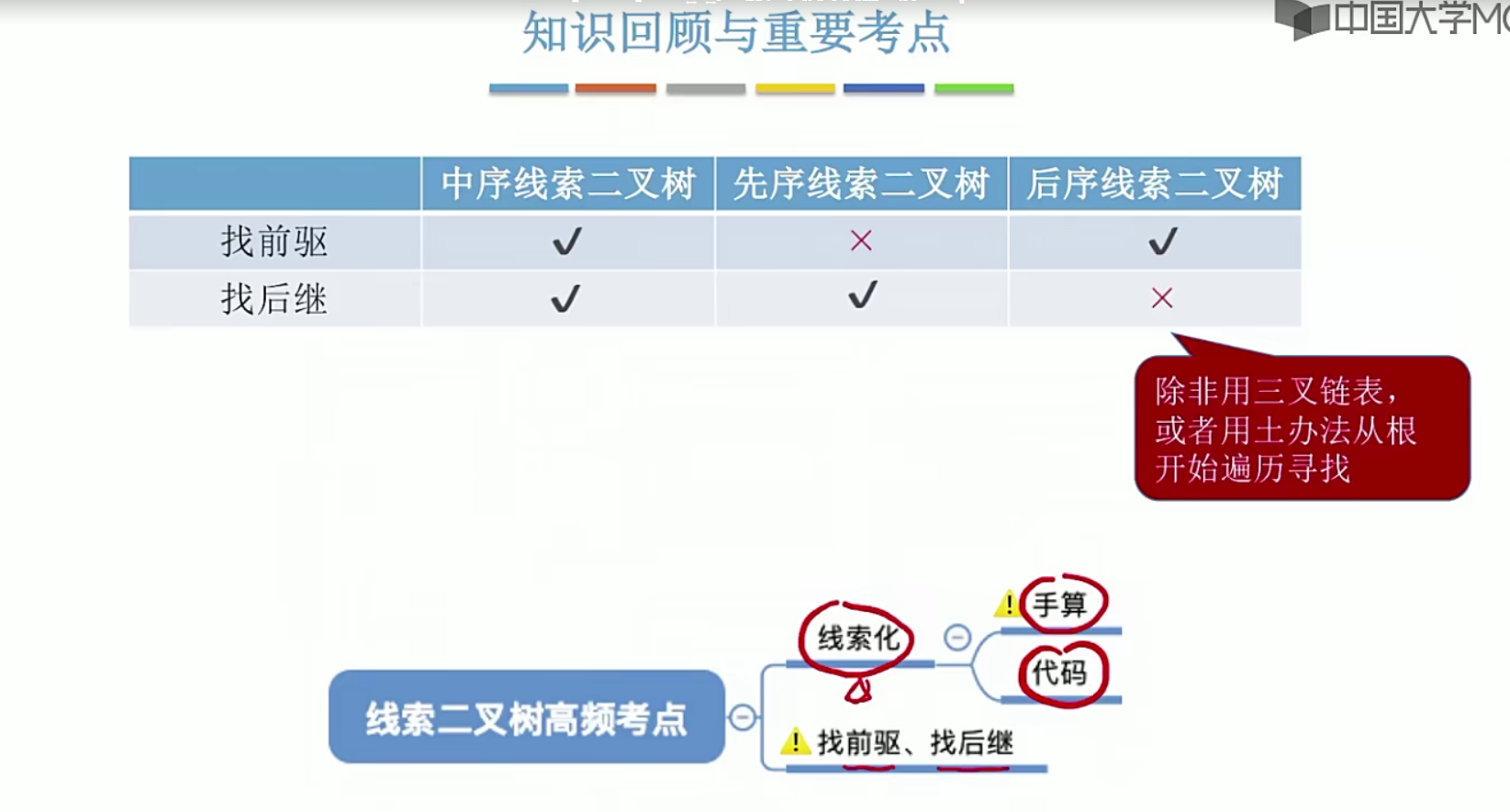
三种的对比


小结


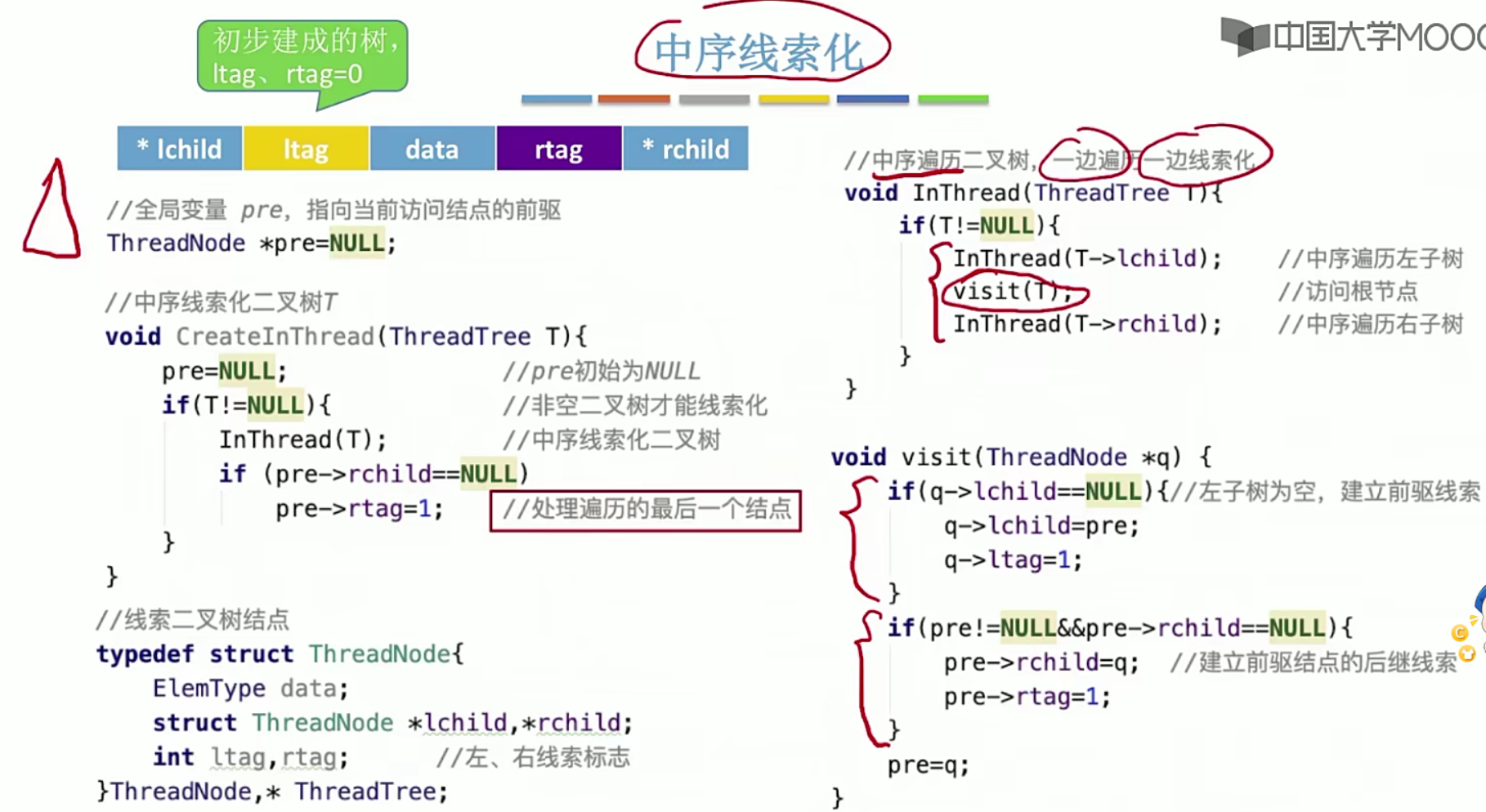
5.9.2二叉树的线索化


思想上 土办法


过程

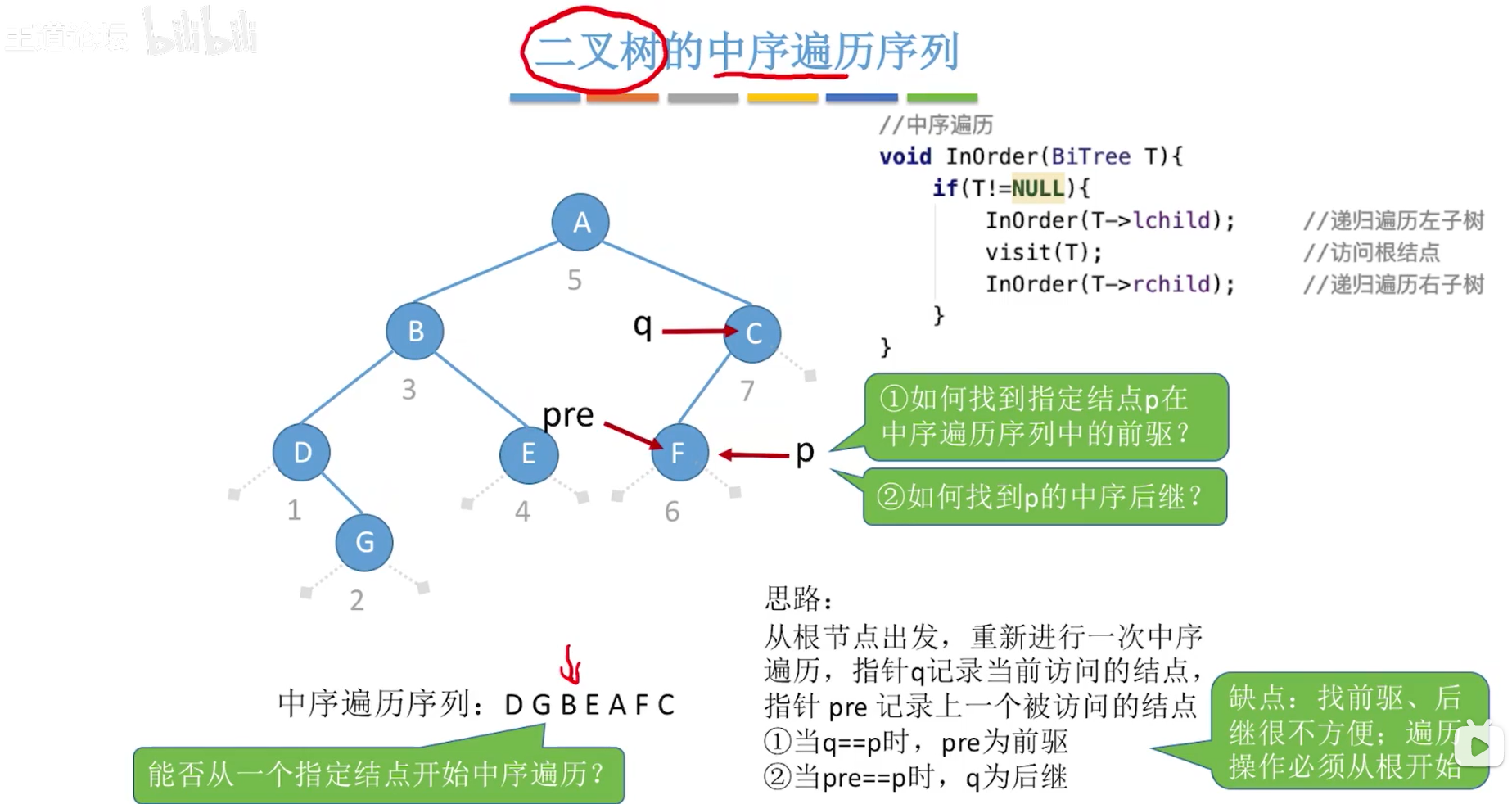
在中序遍历中 第一次遍历到 D 此时 pre =null q=D不等 p 则 pre指向D

​ 第二次遍历 G pre=D q=G不等p pre指向 G

......以此类推 最后 pre=A q=F=p 则 p的前驱是A

中序线索化

先序线索化

后序线索化

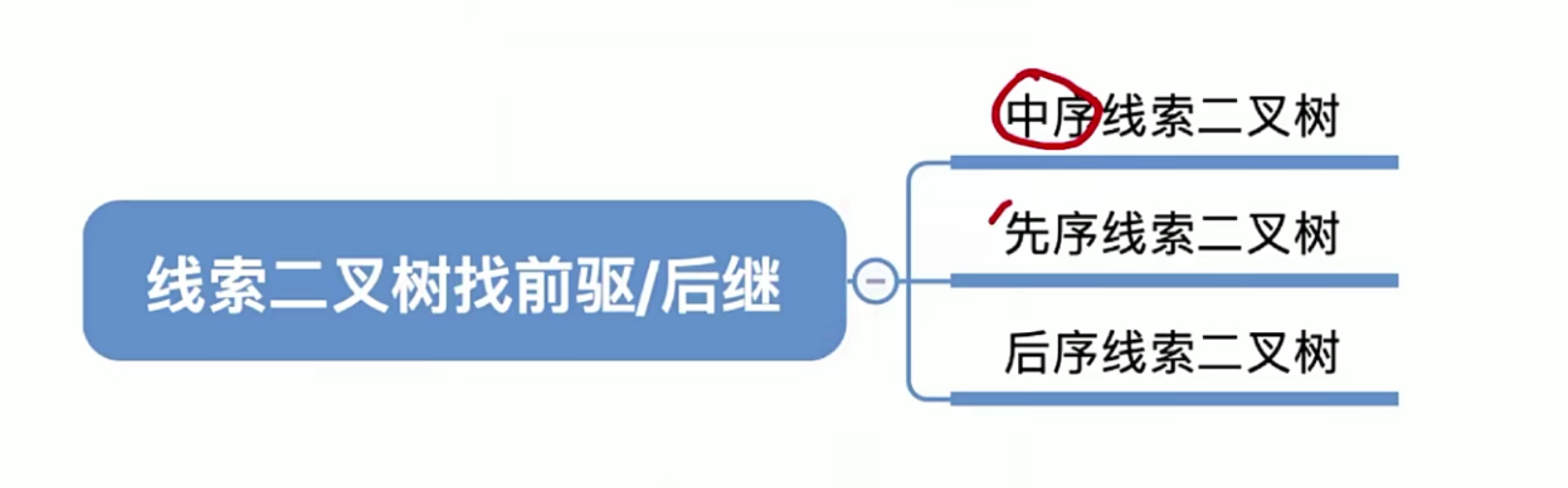
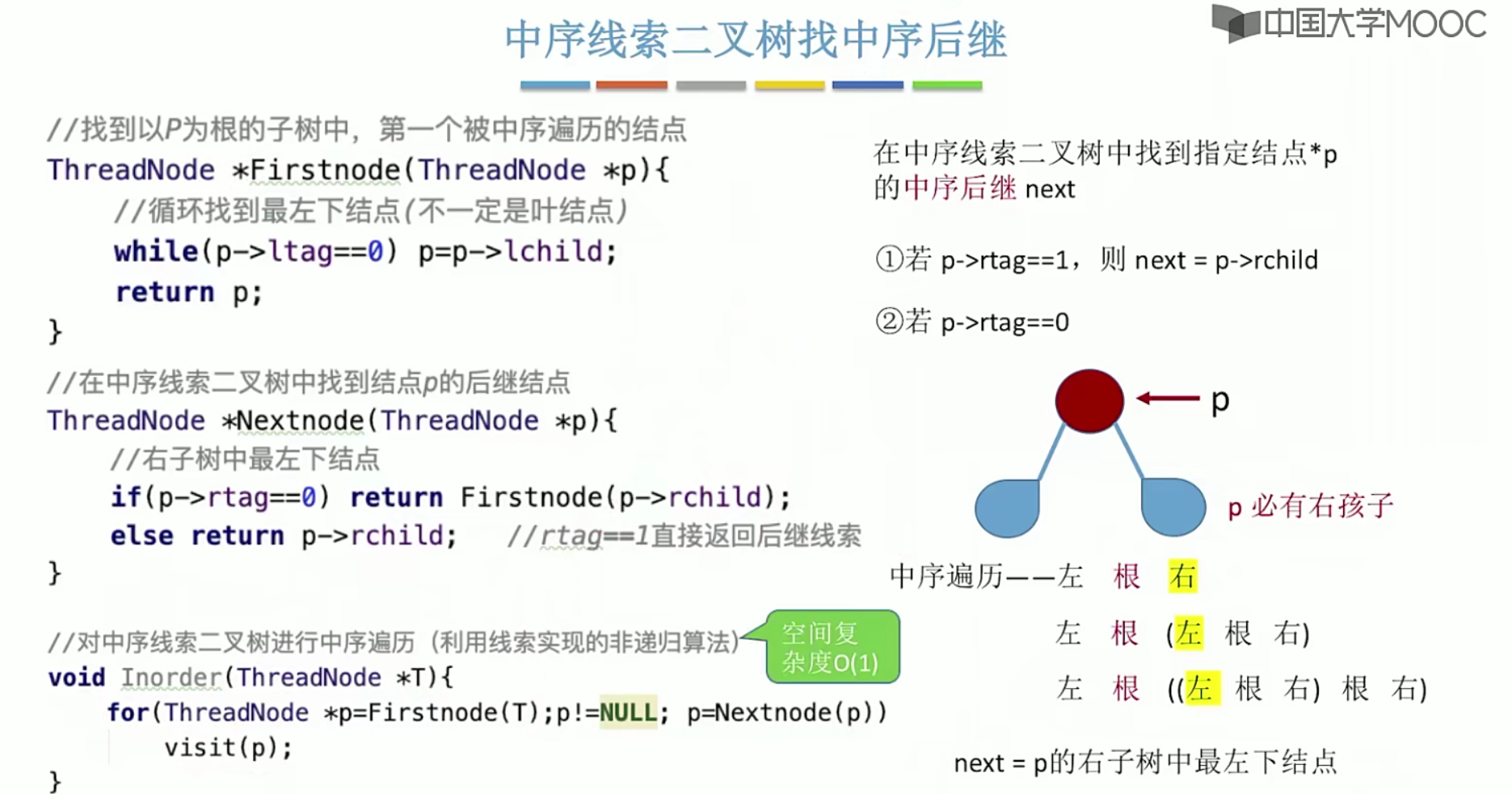
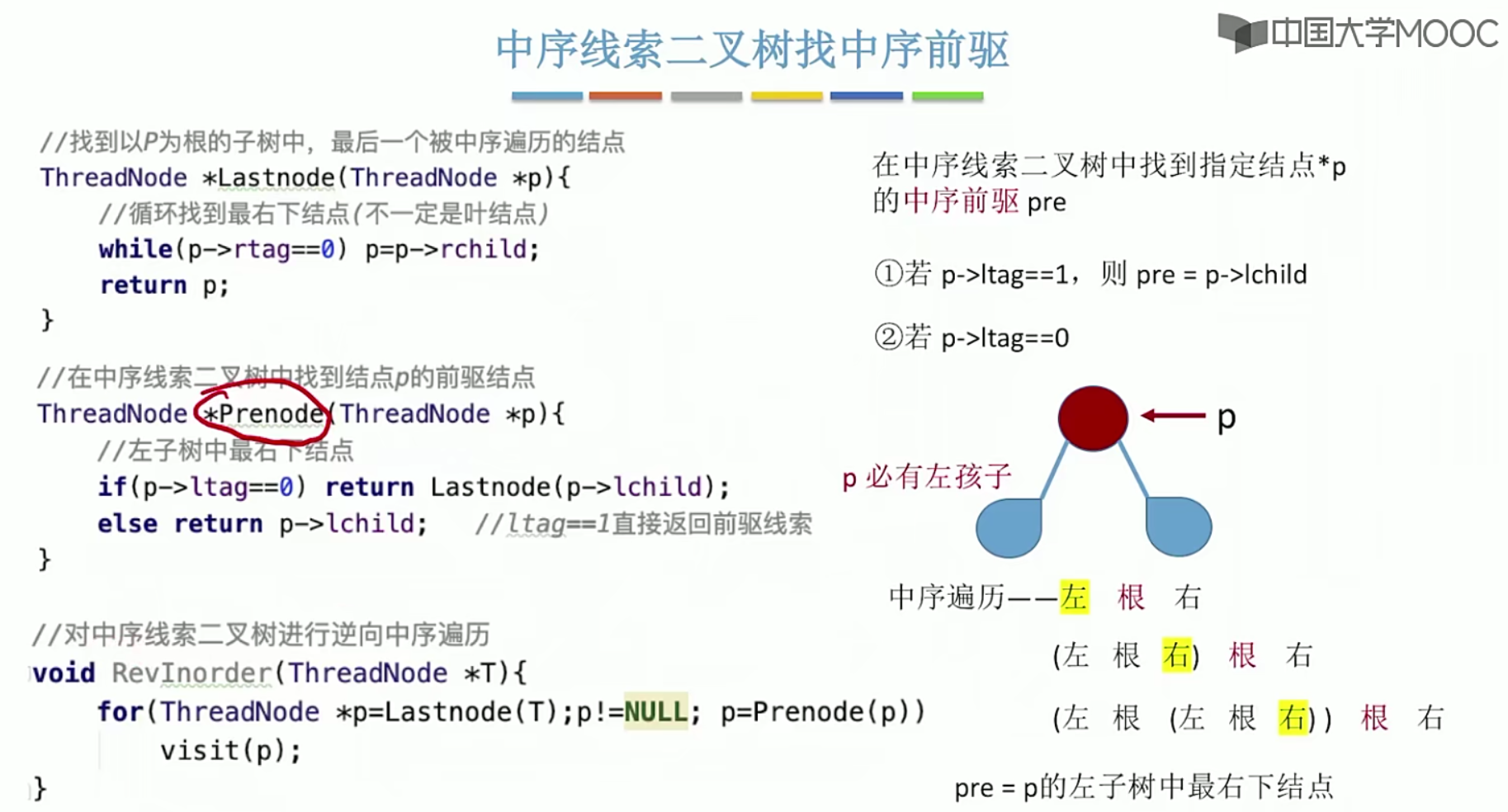
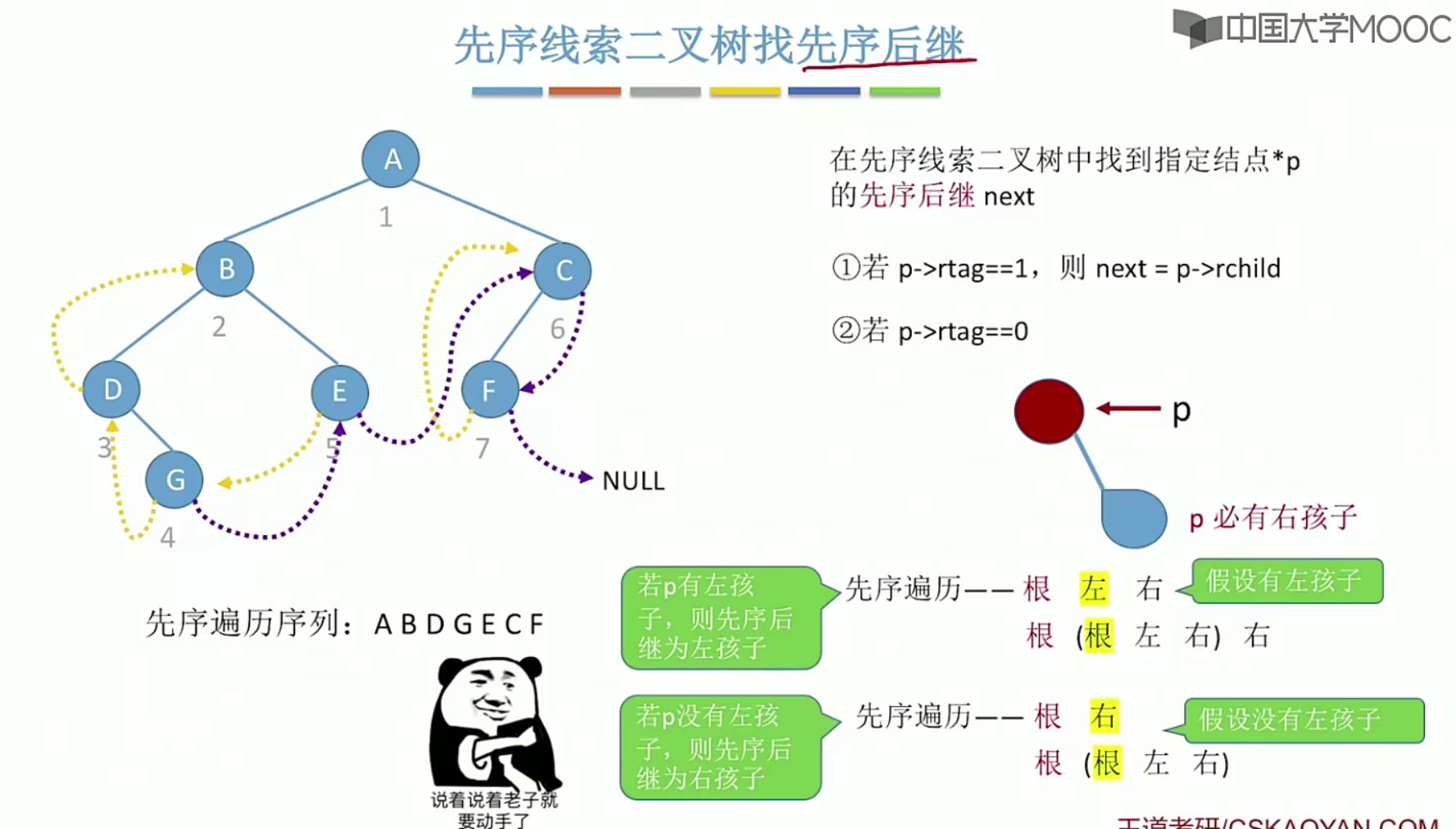
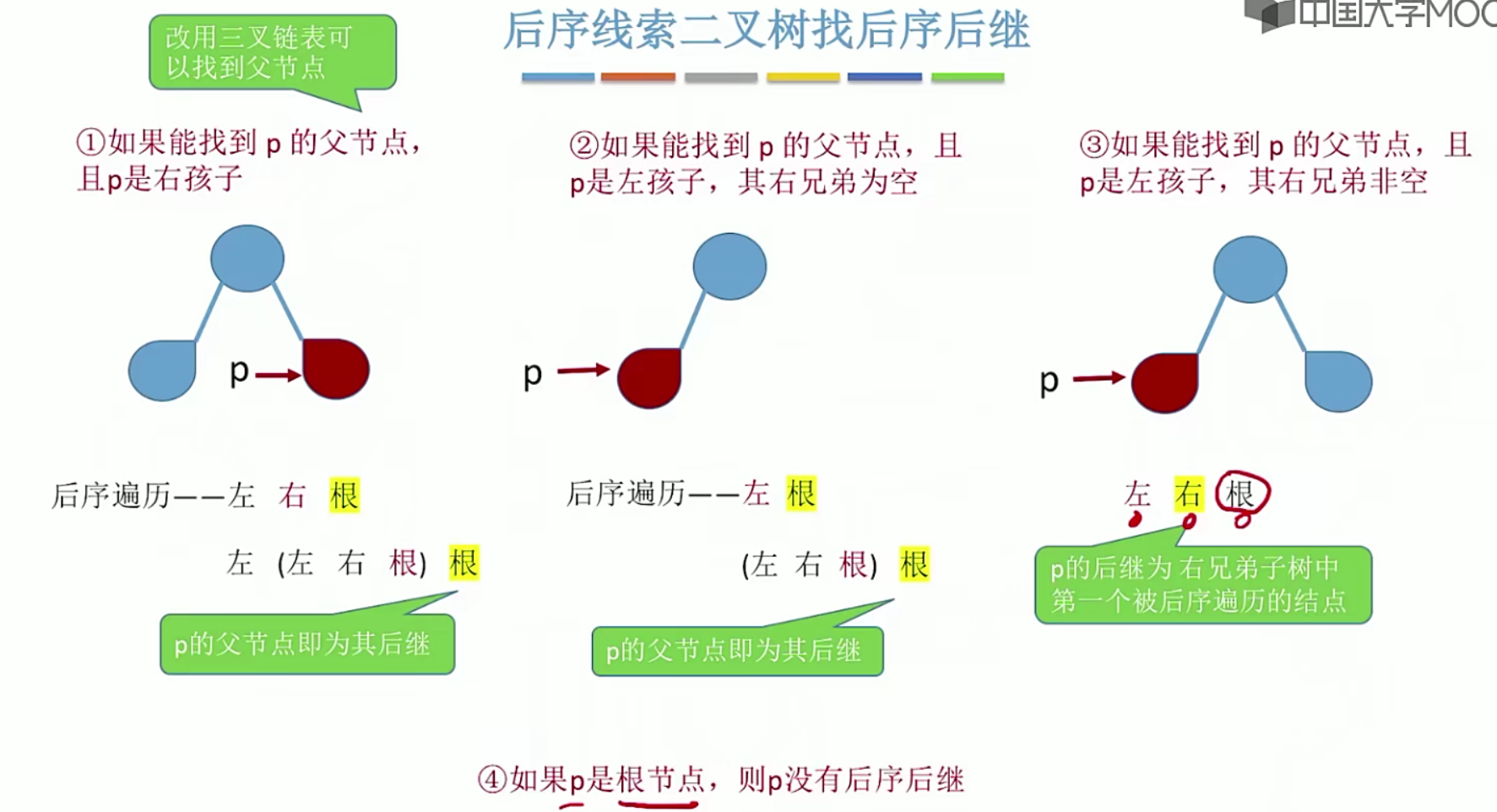
5.9.3线索二叉树找前驱，后继

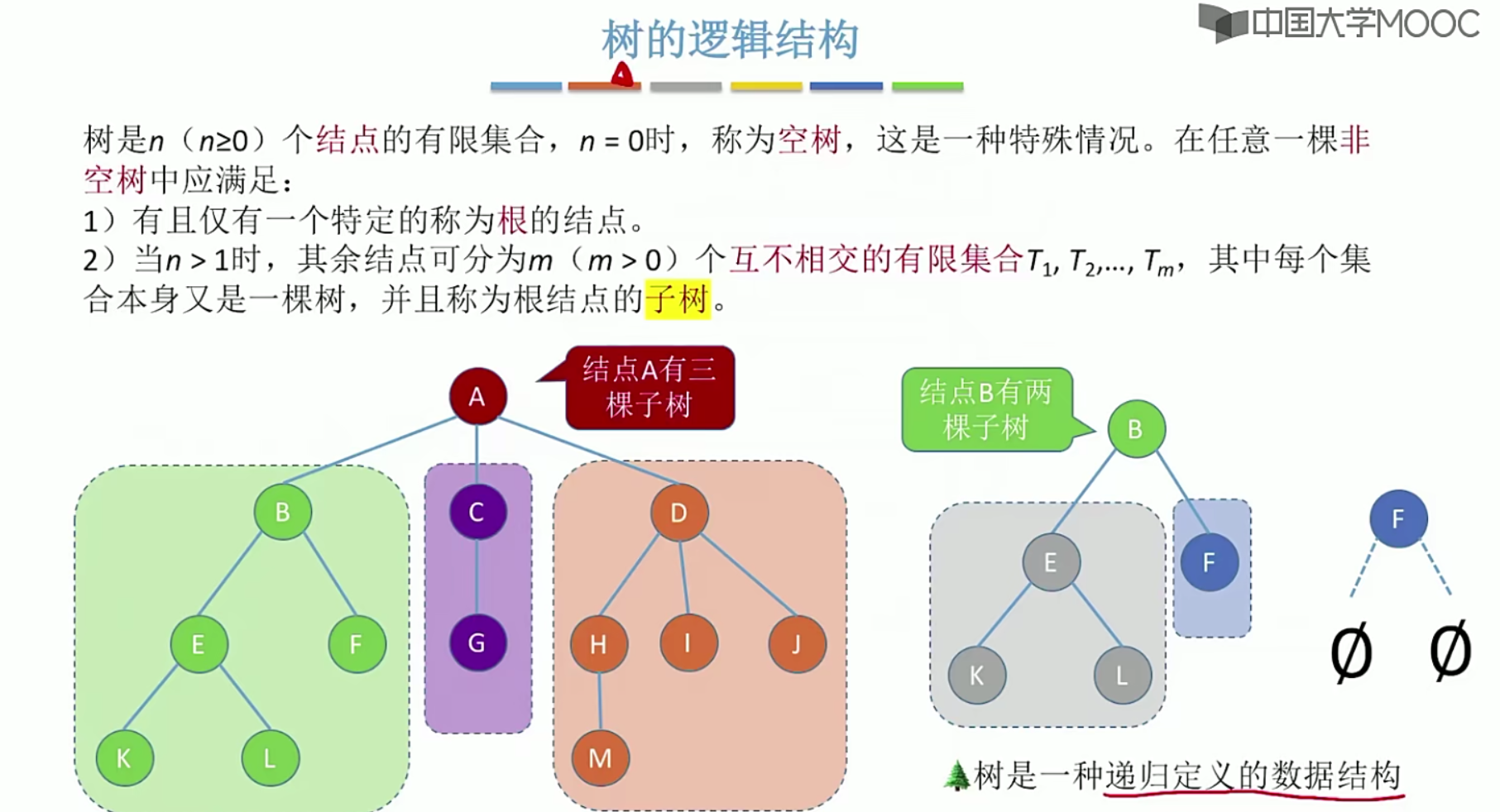
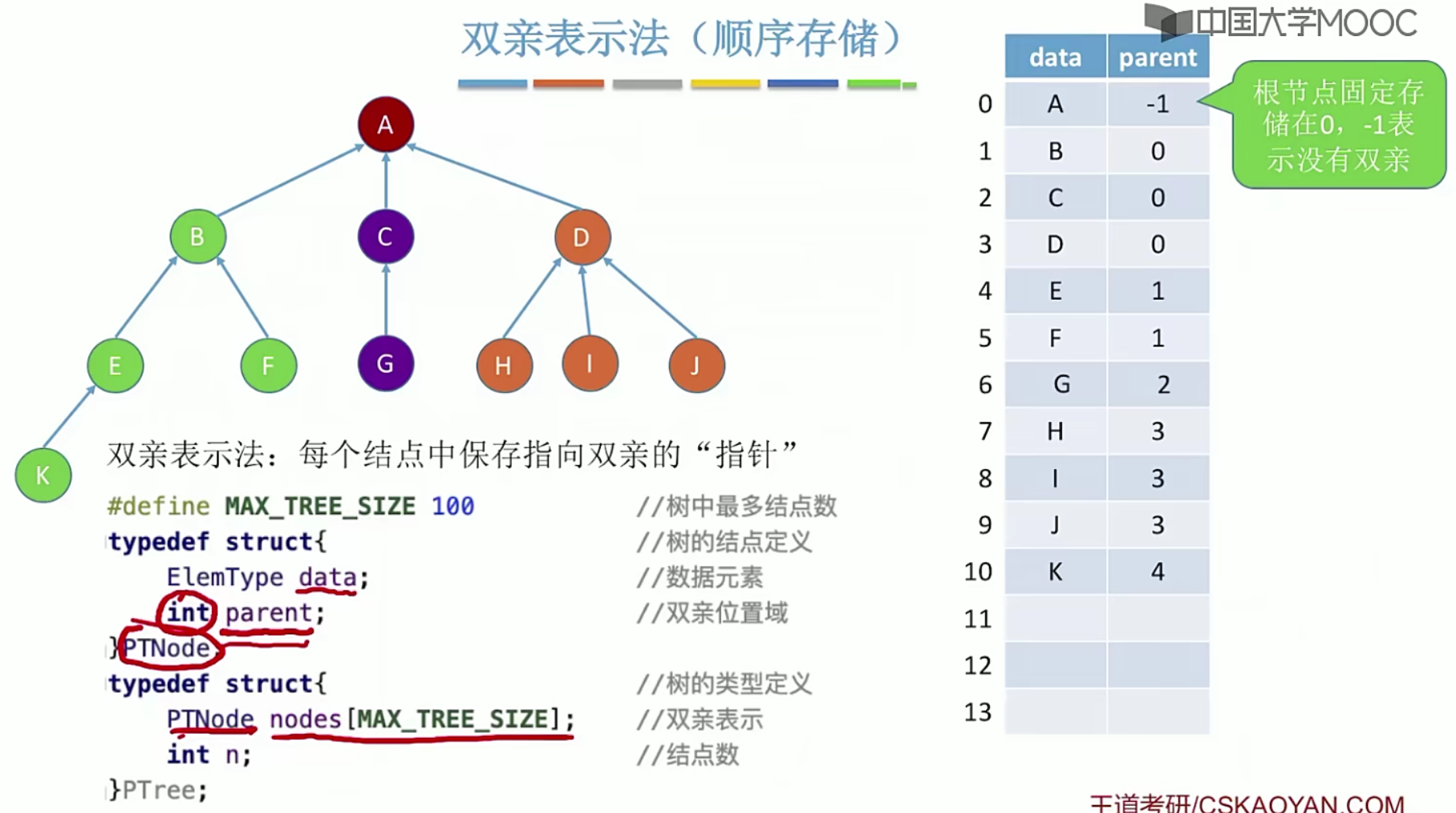
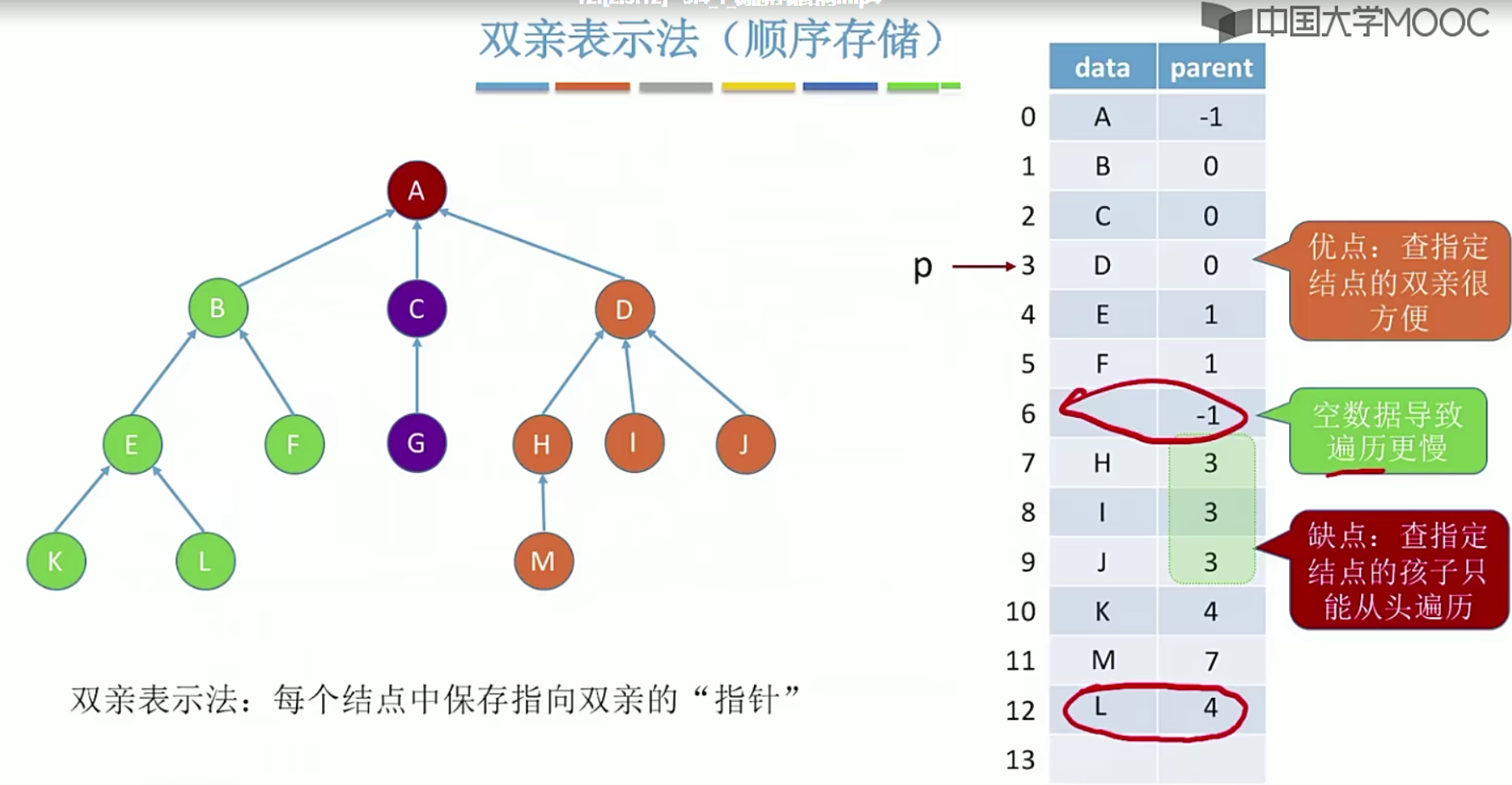
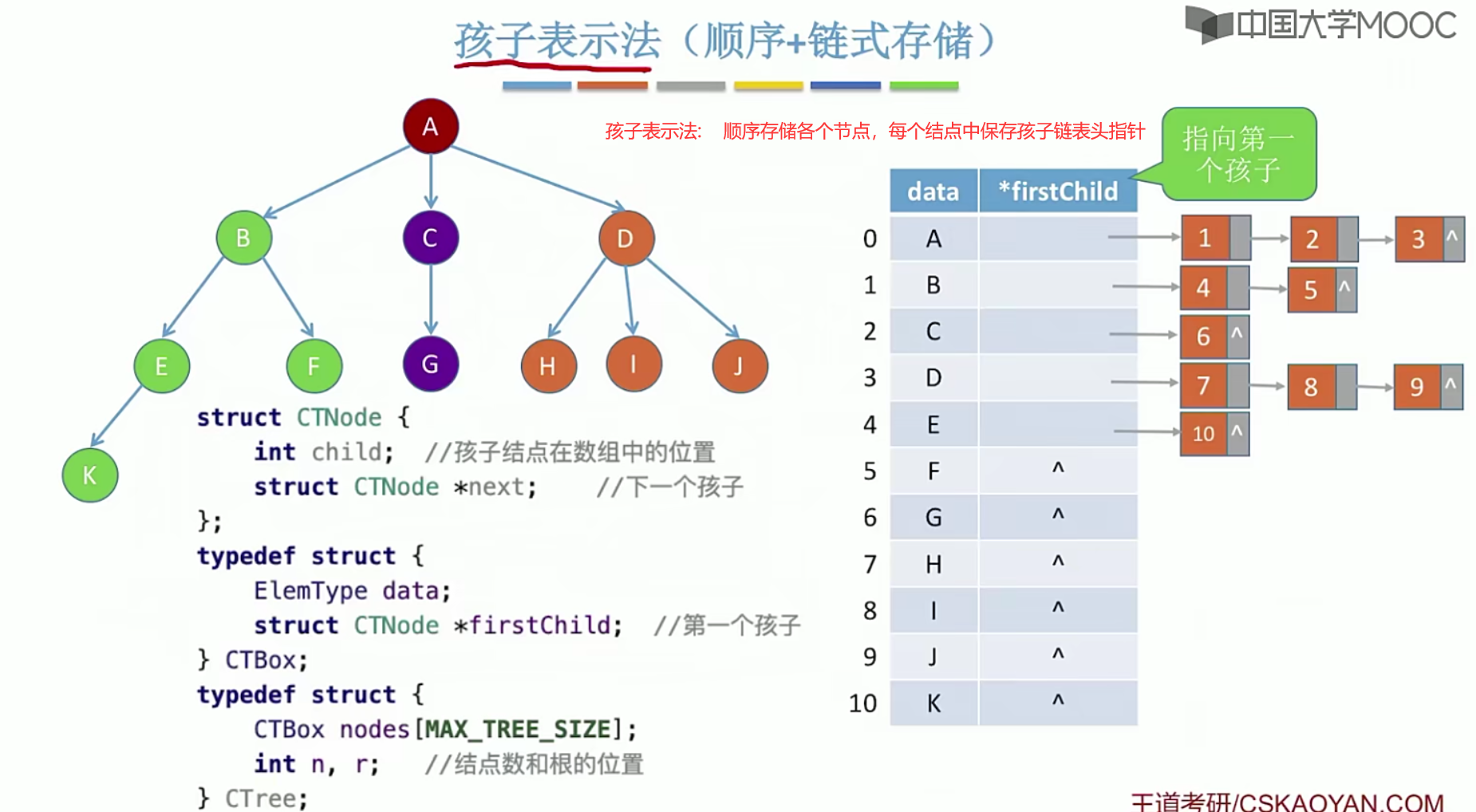
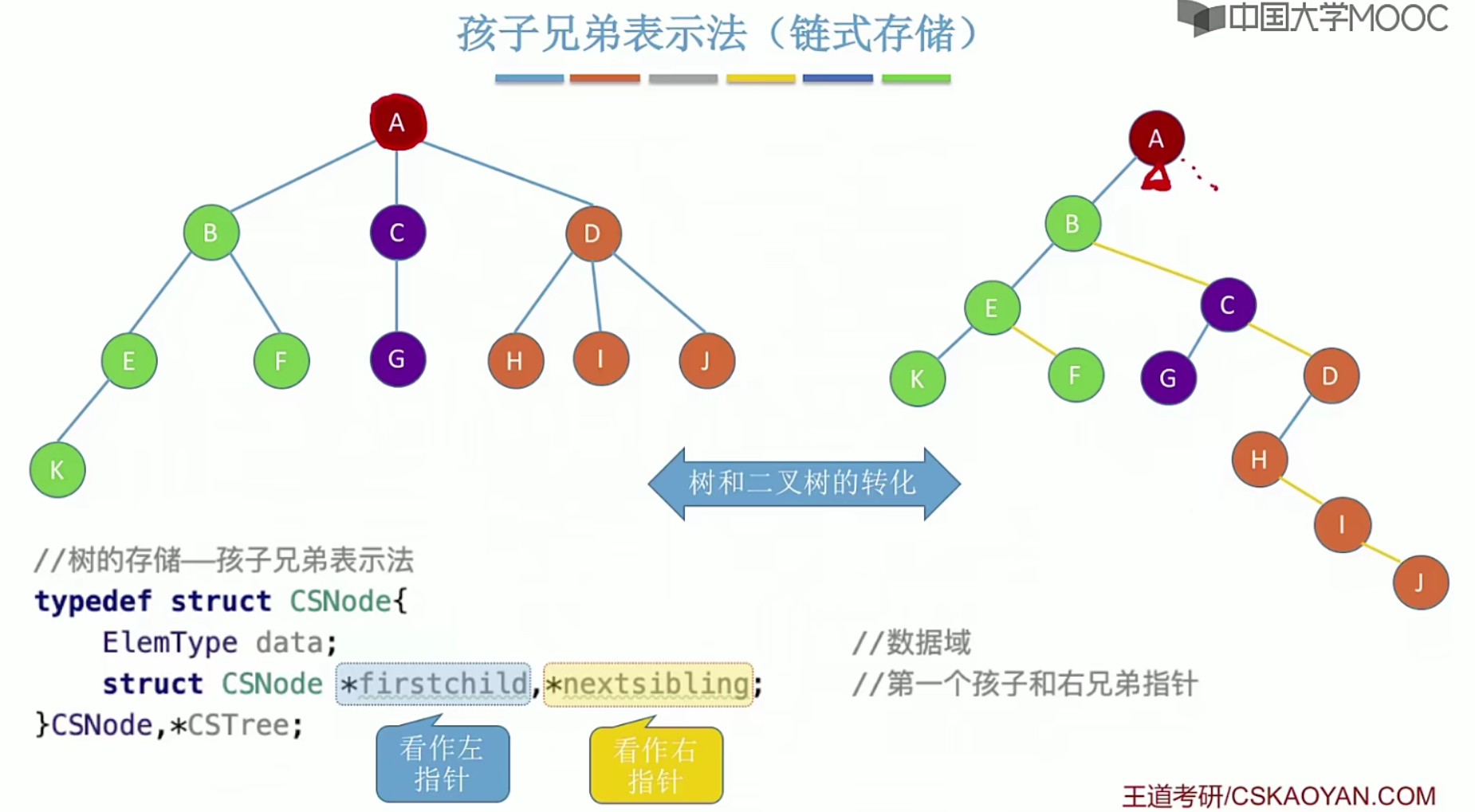
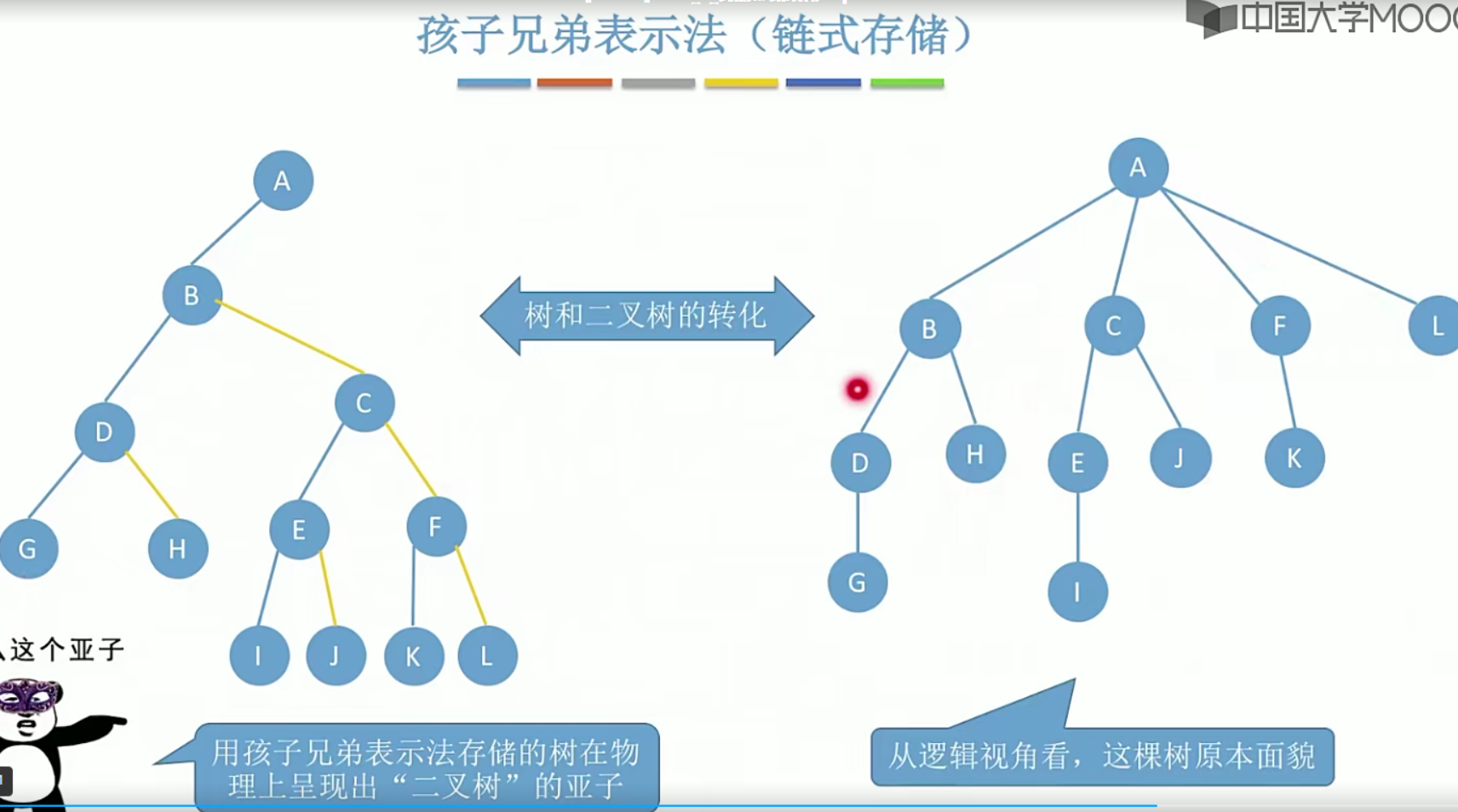
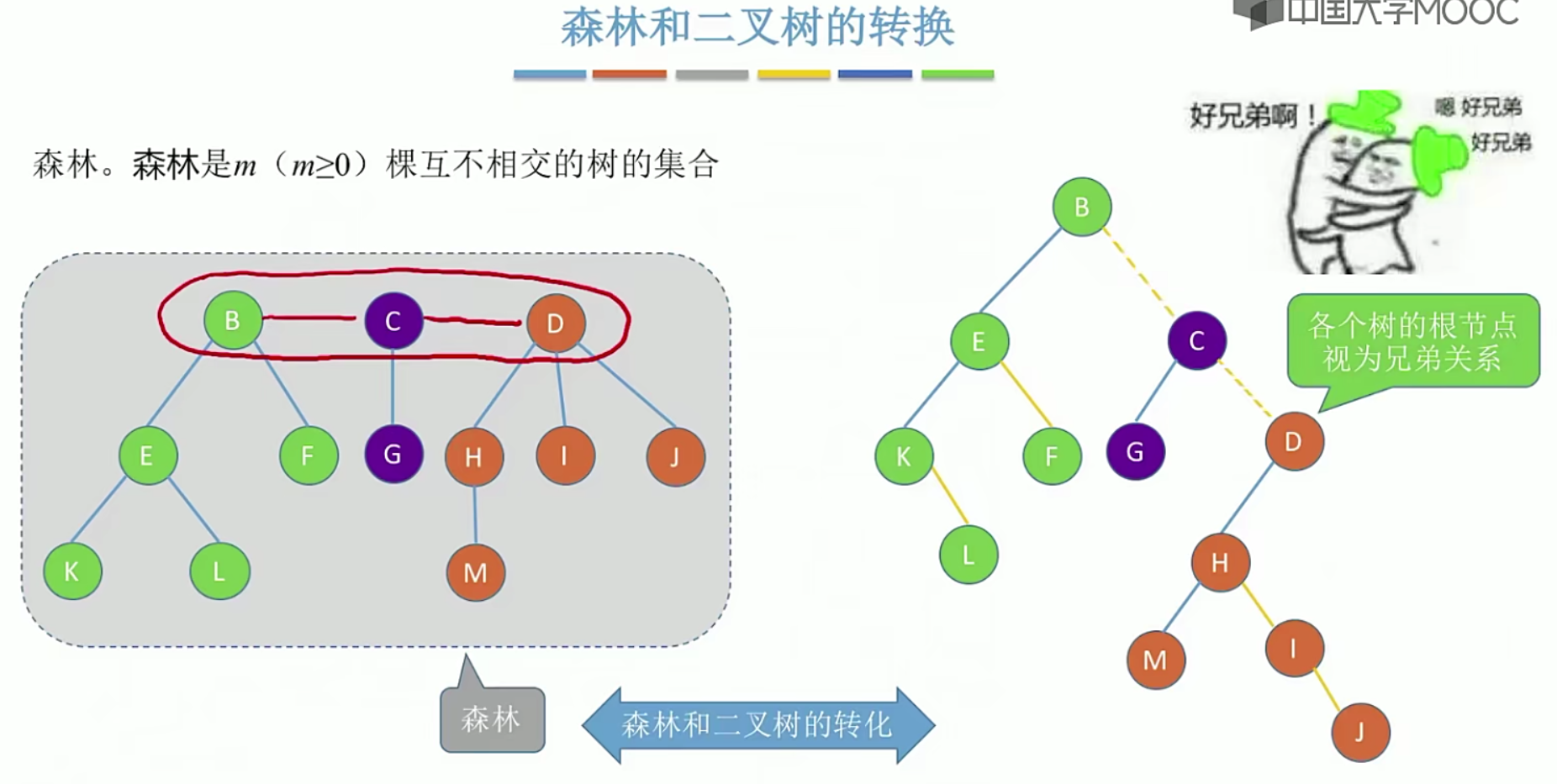
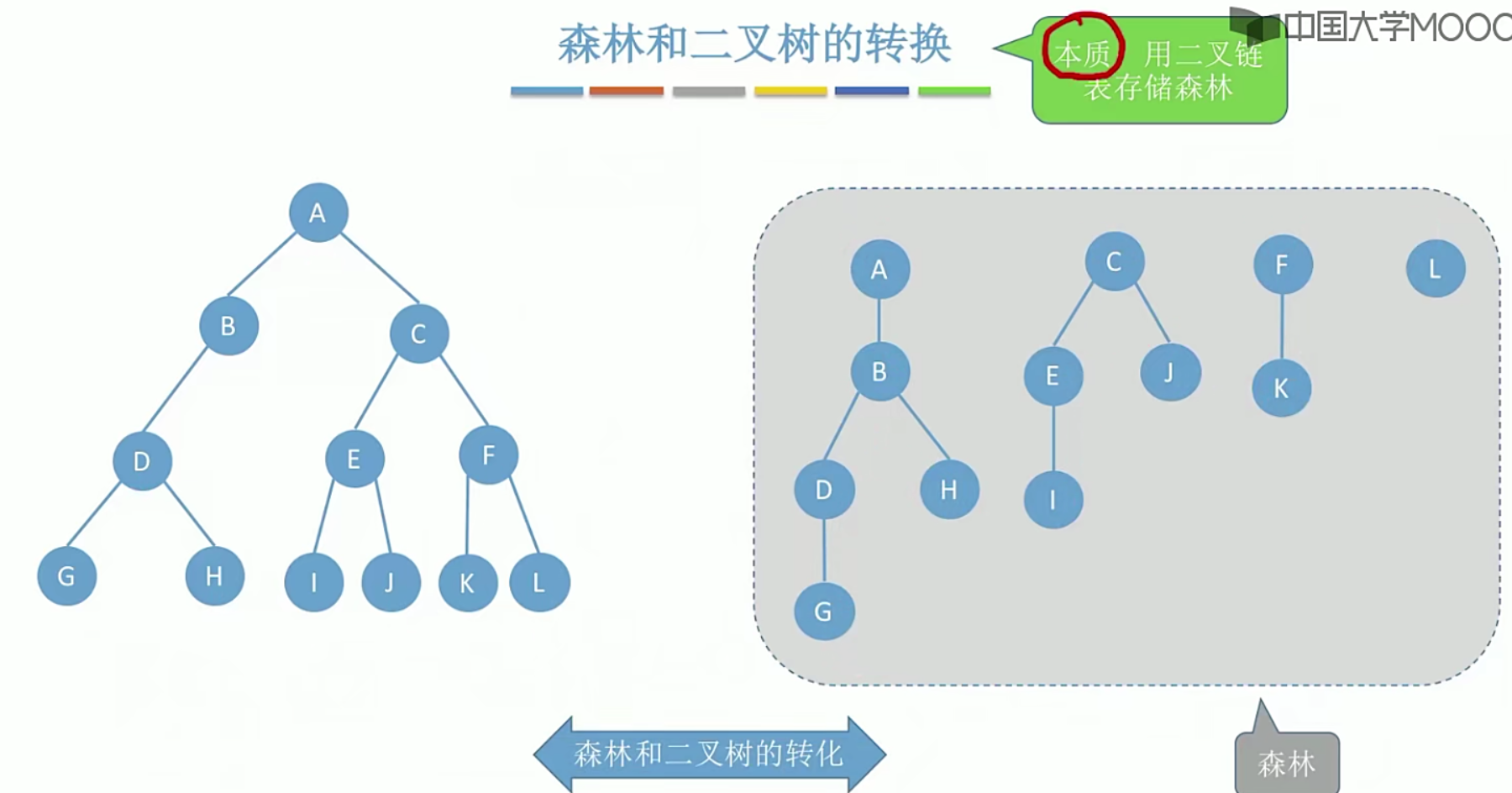
5.10树的存储结构

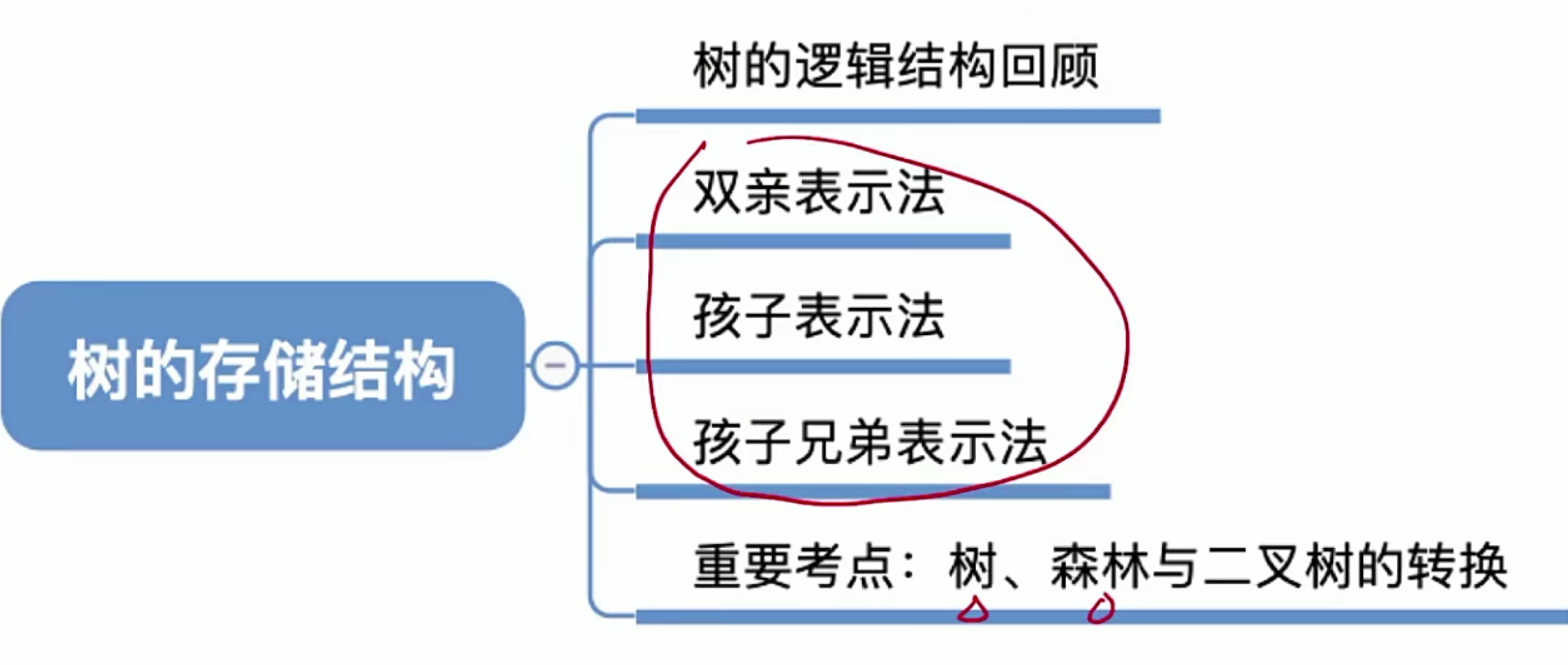
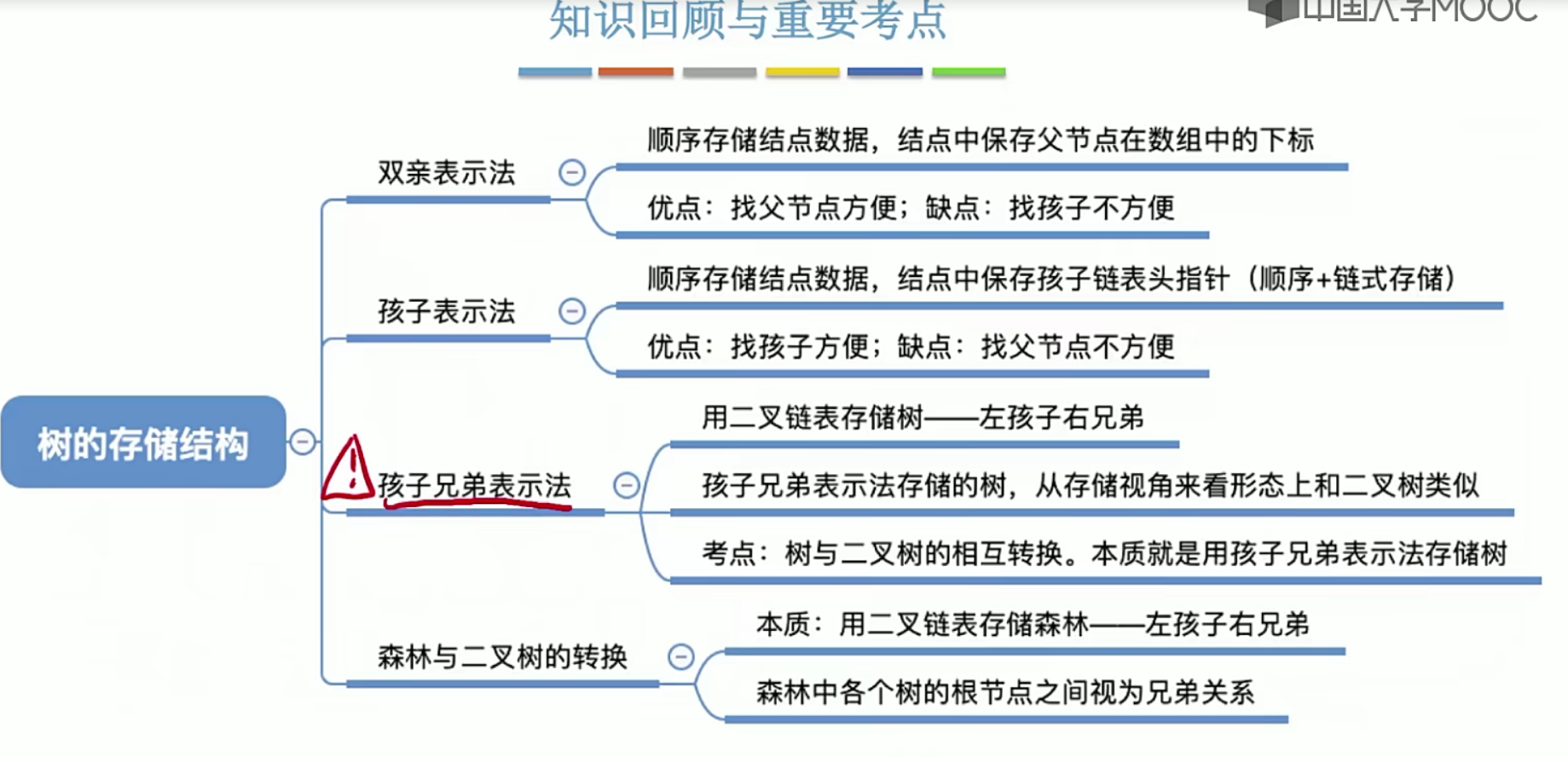
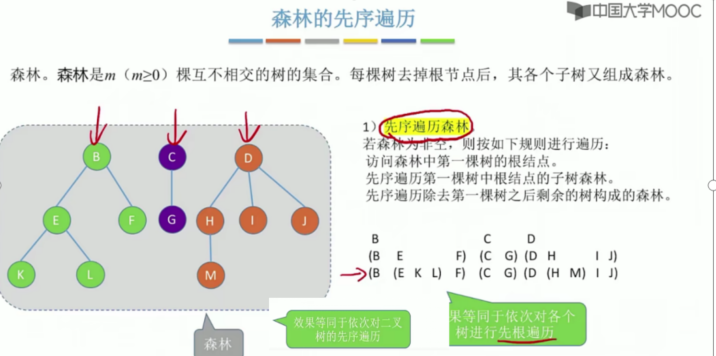
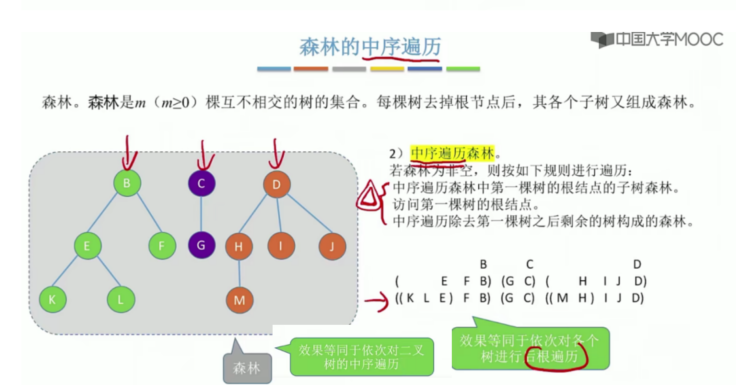
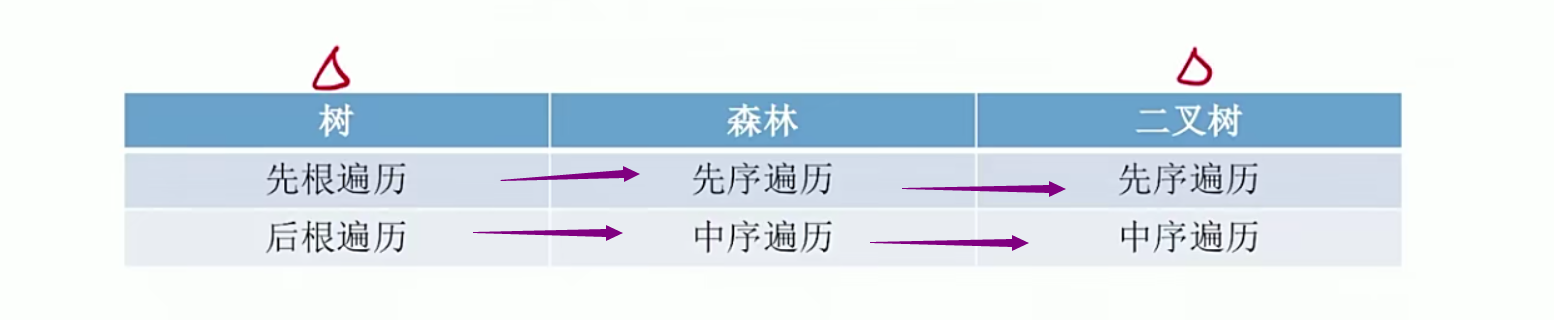
5.11树和森林的遍历

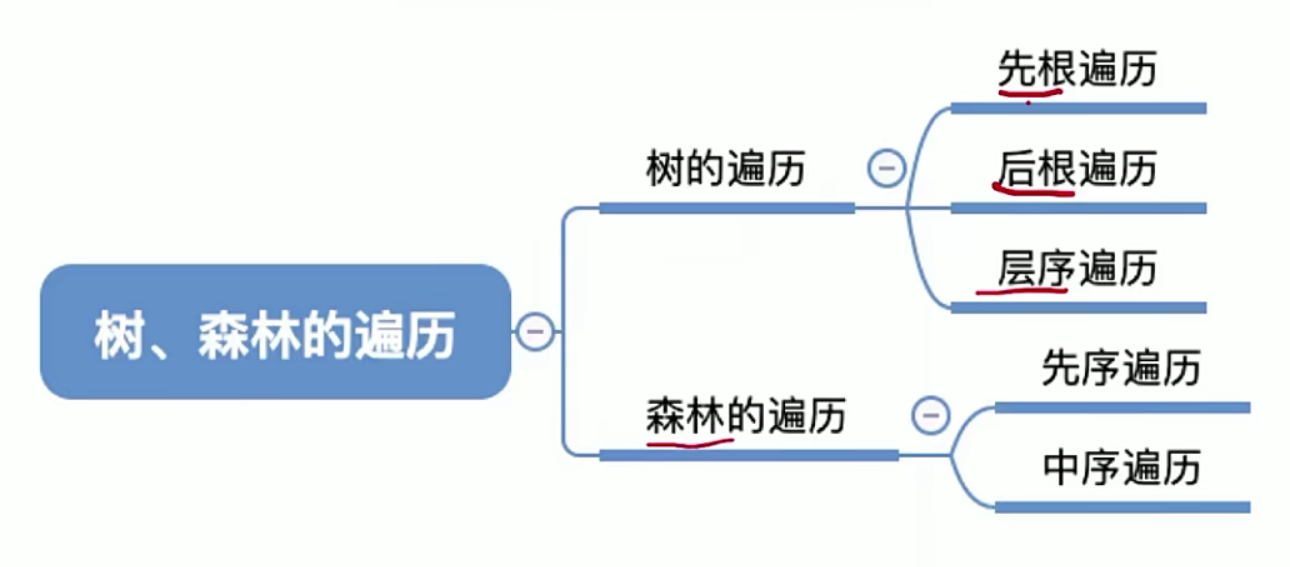
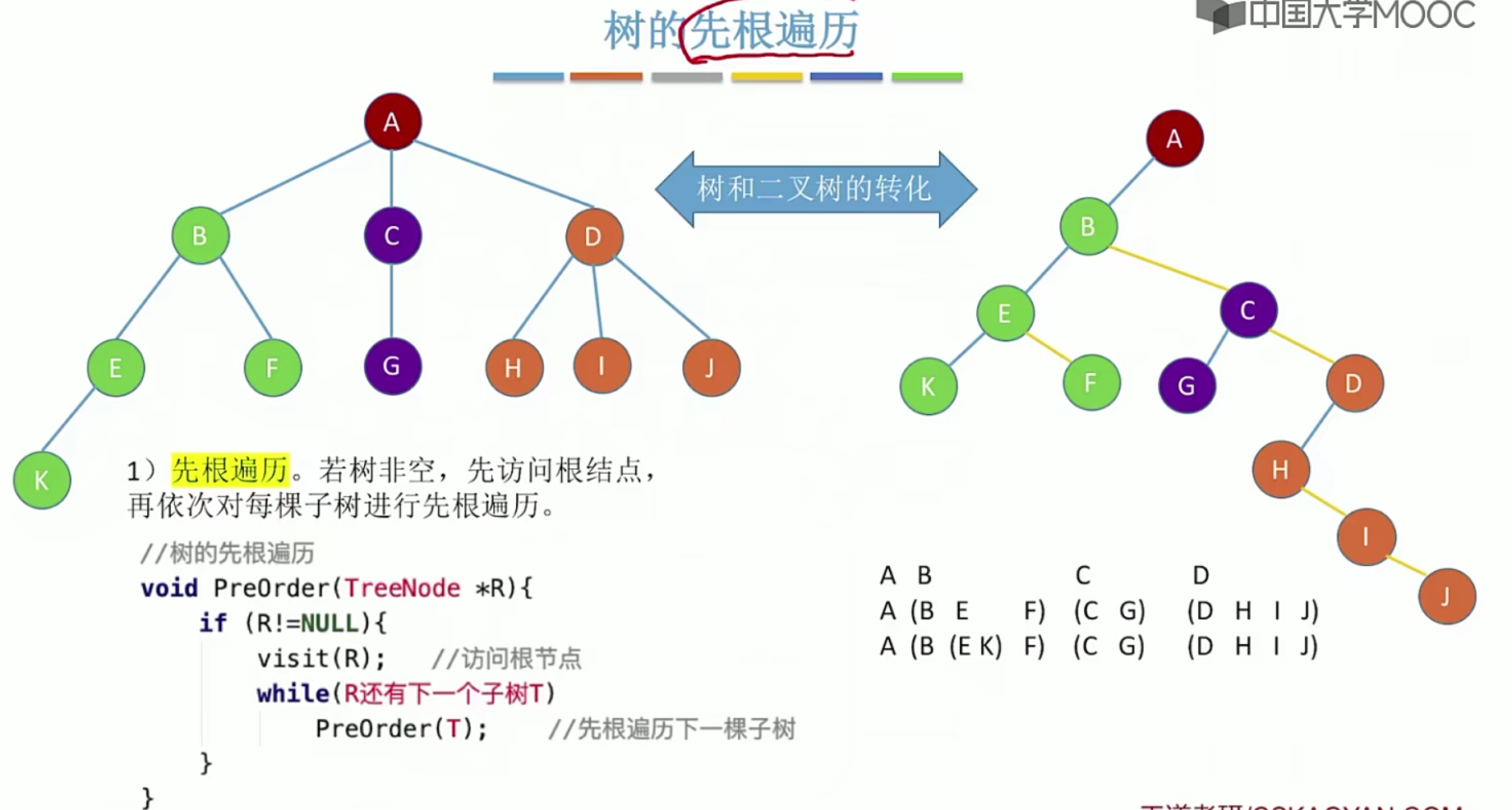
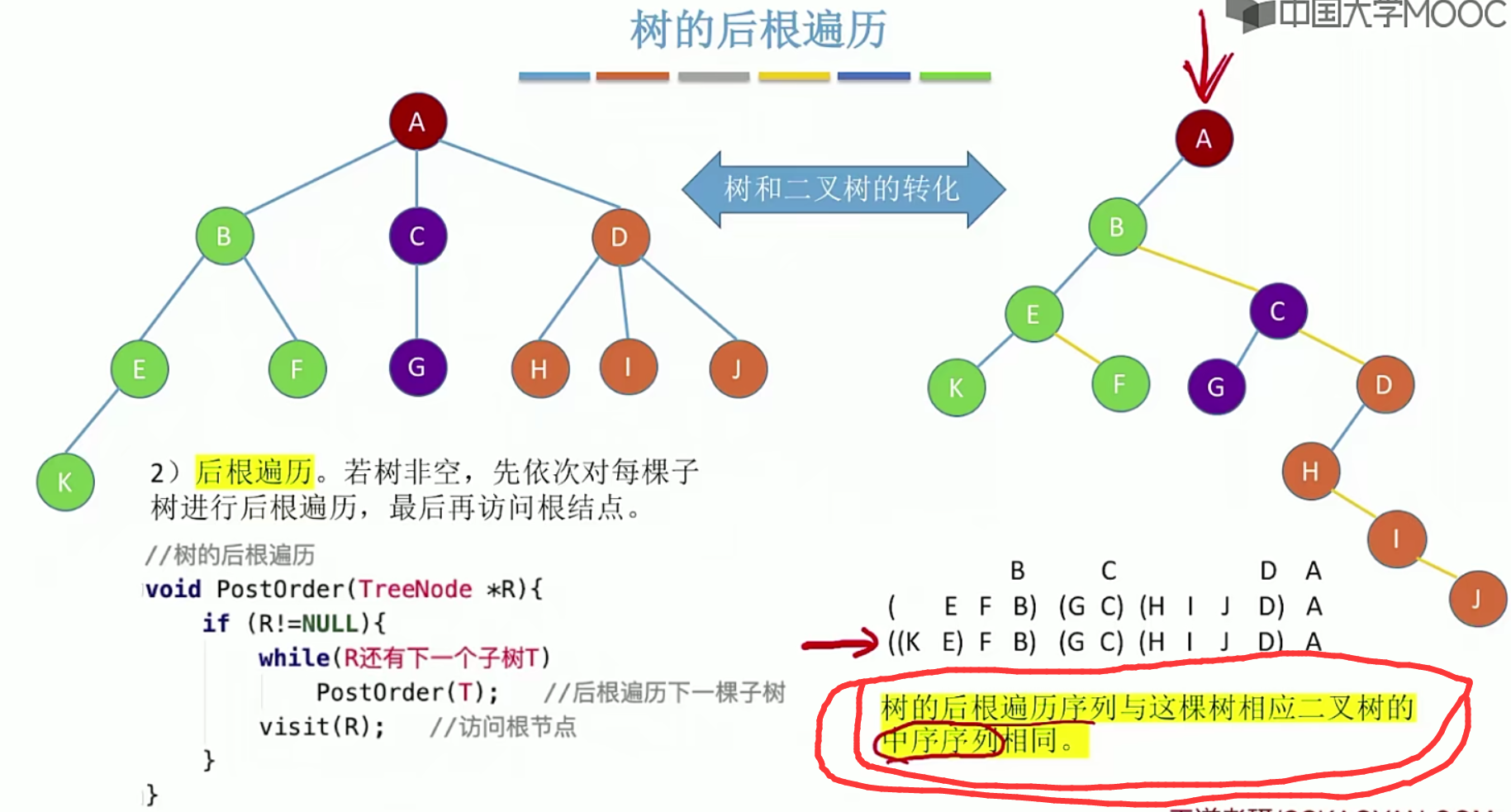
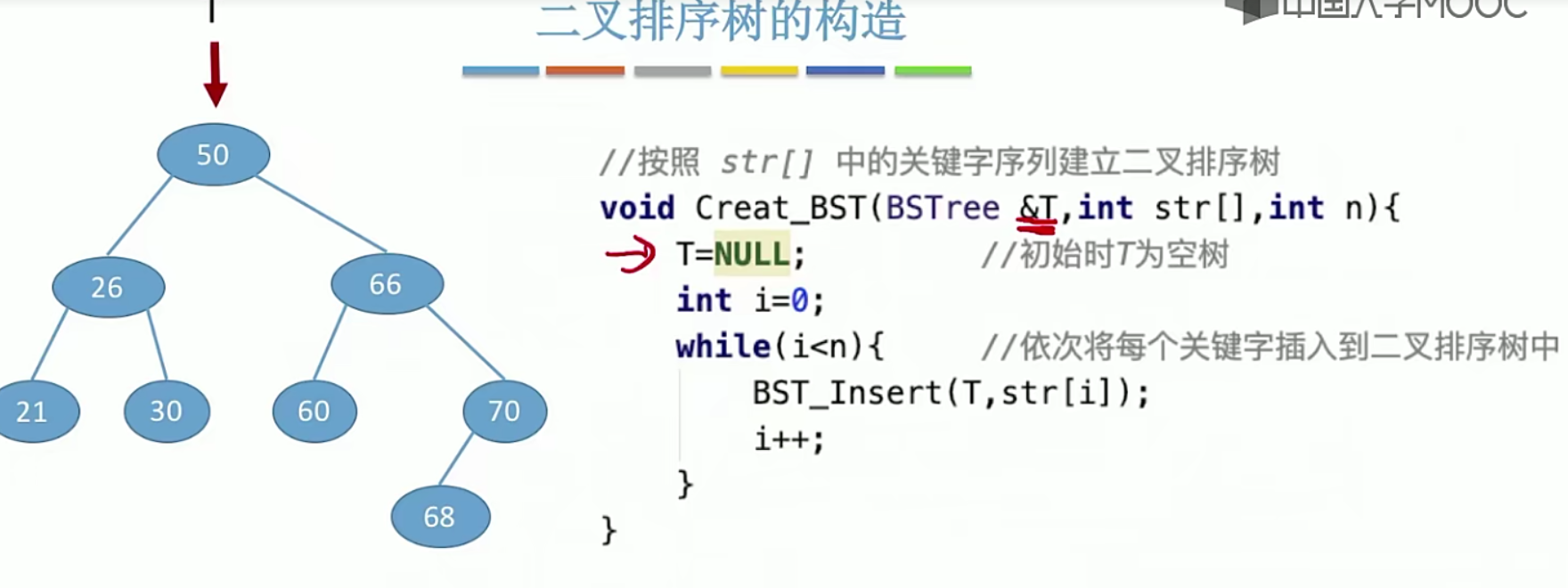
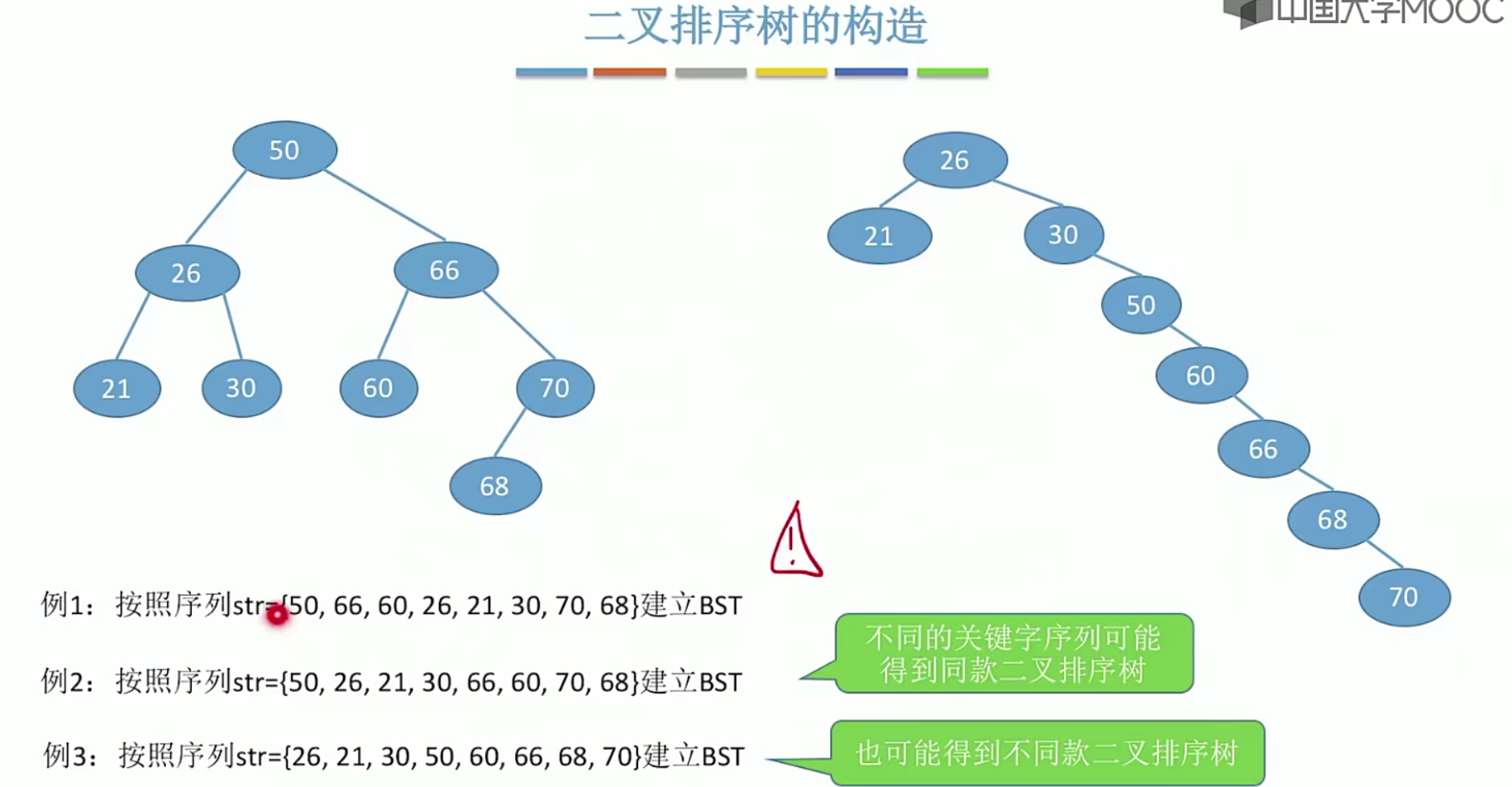
5.12 二叉排序树

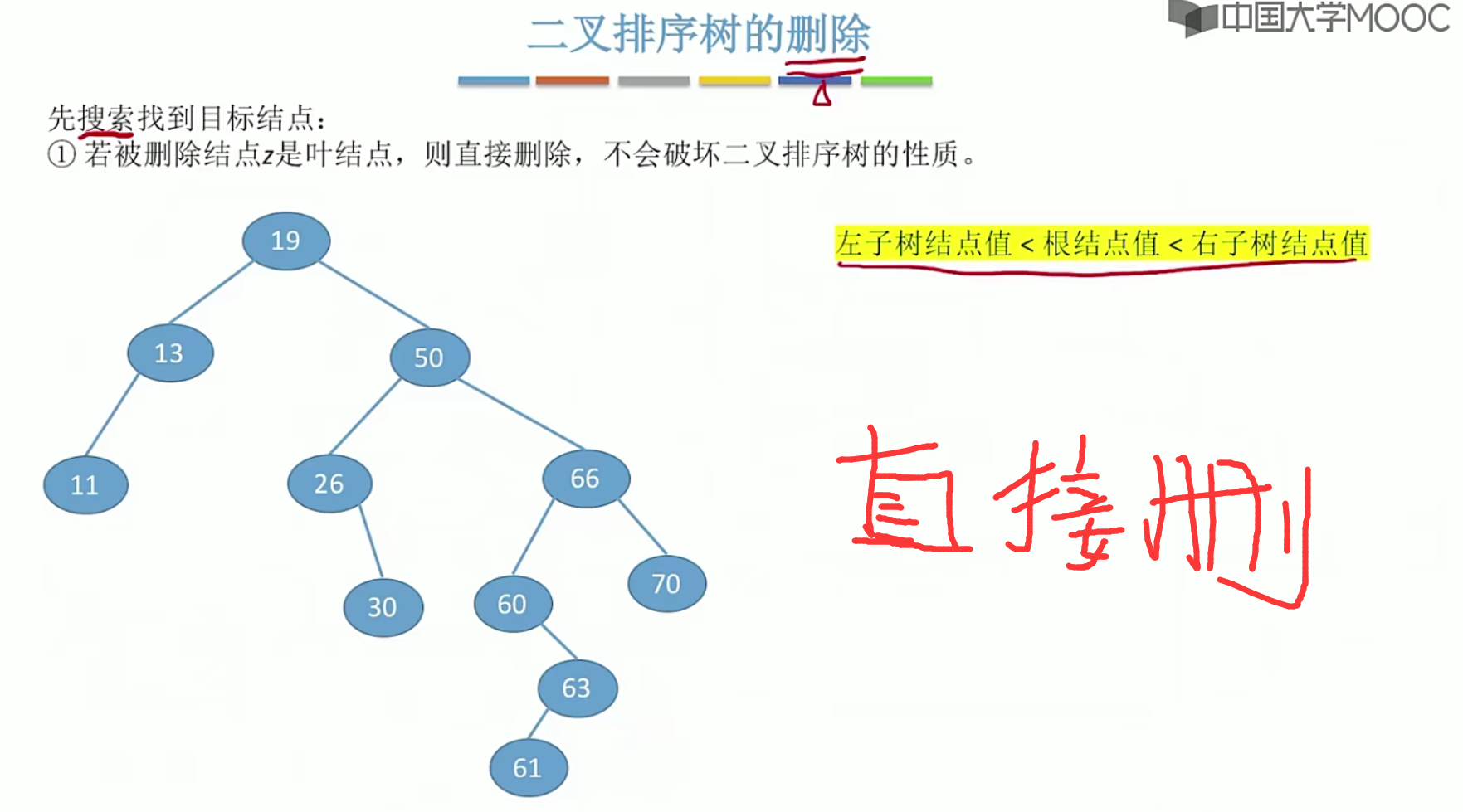
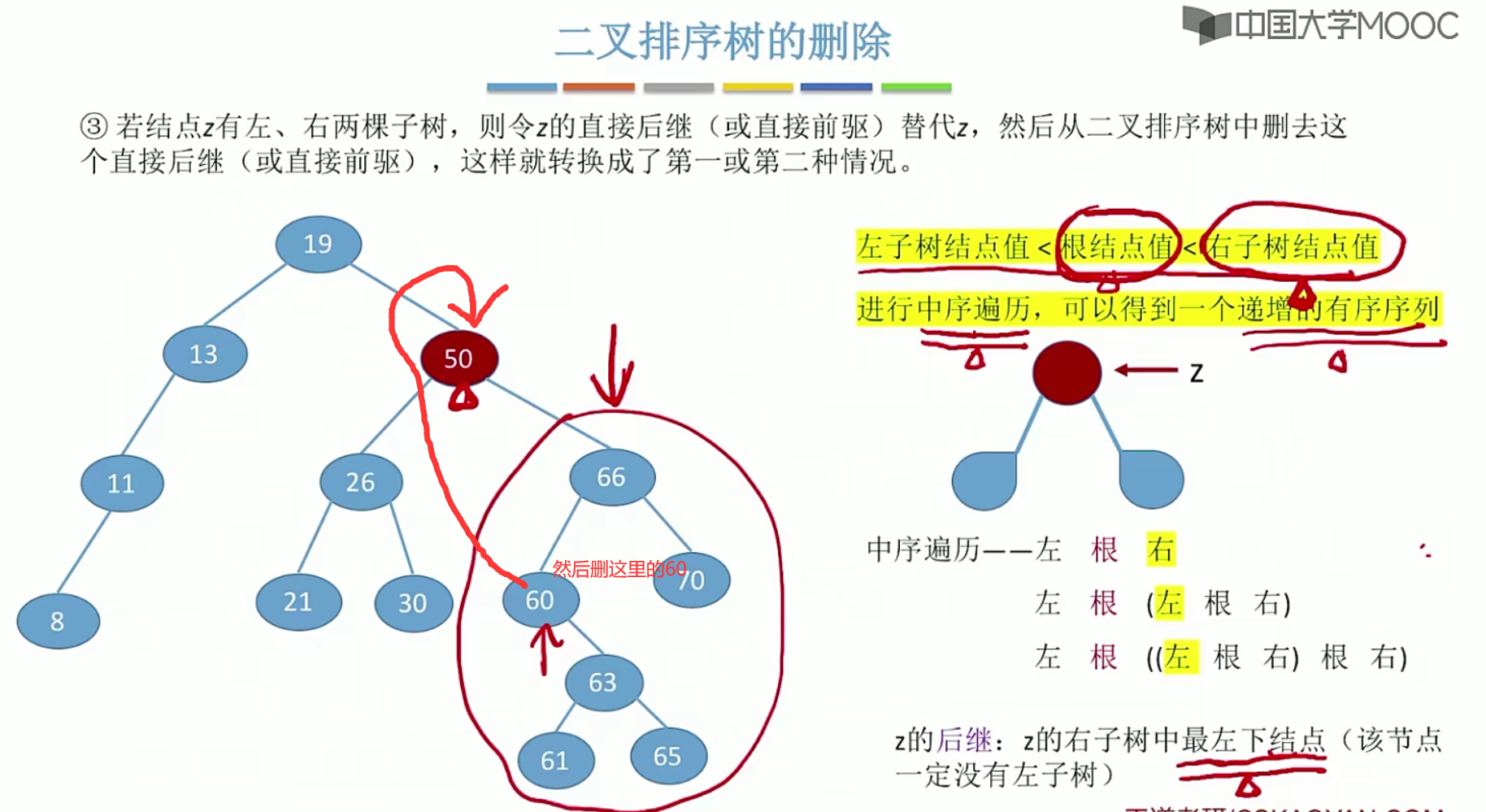
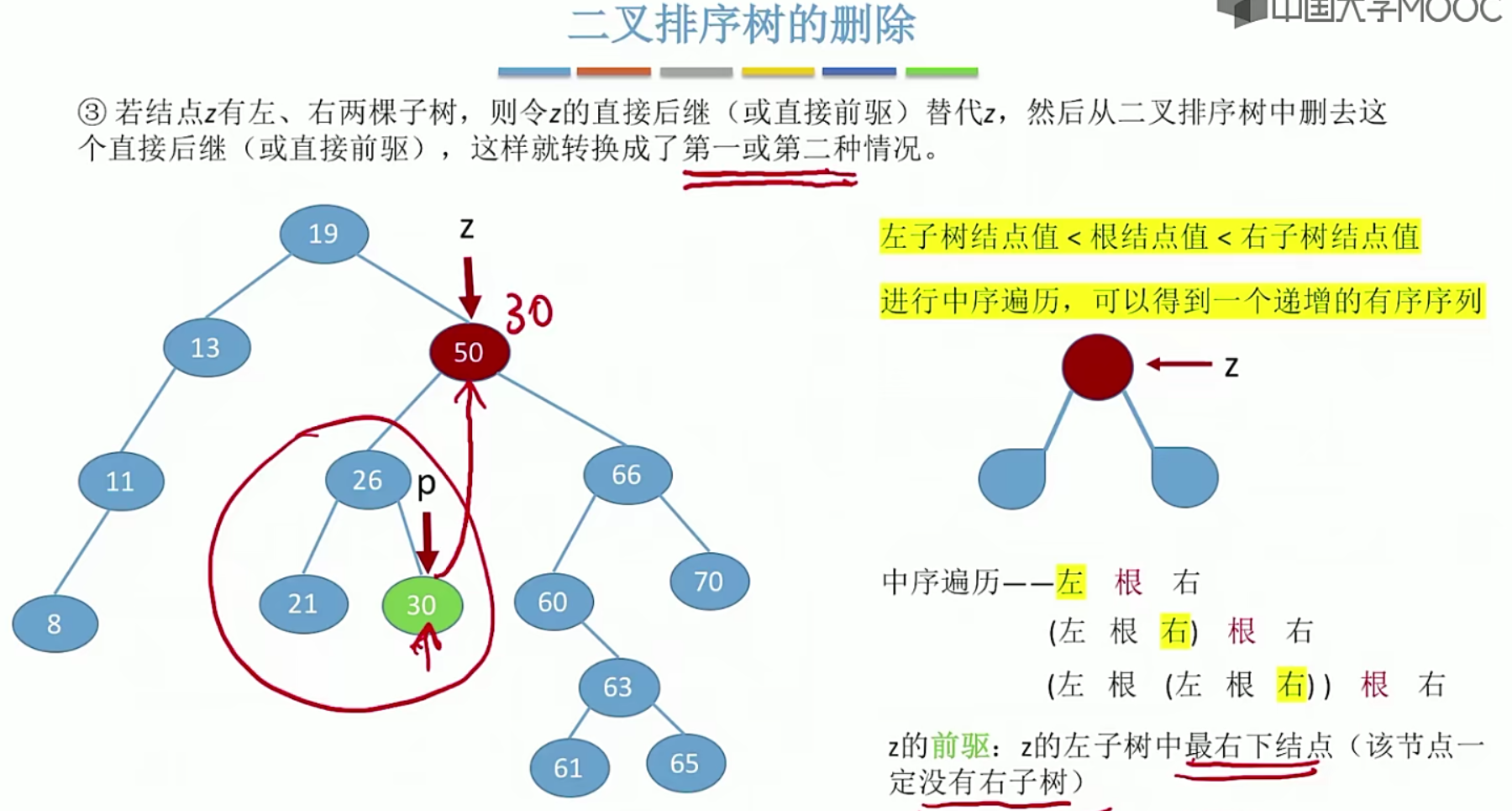
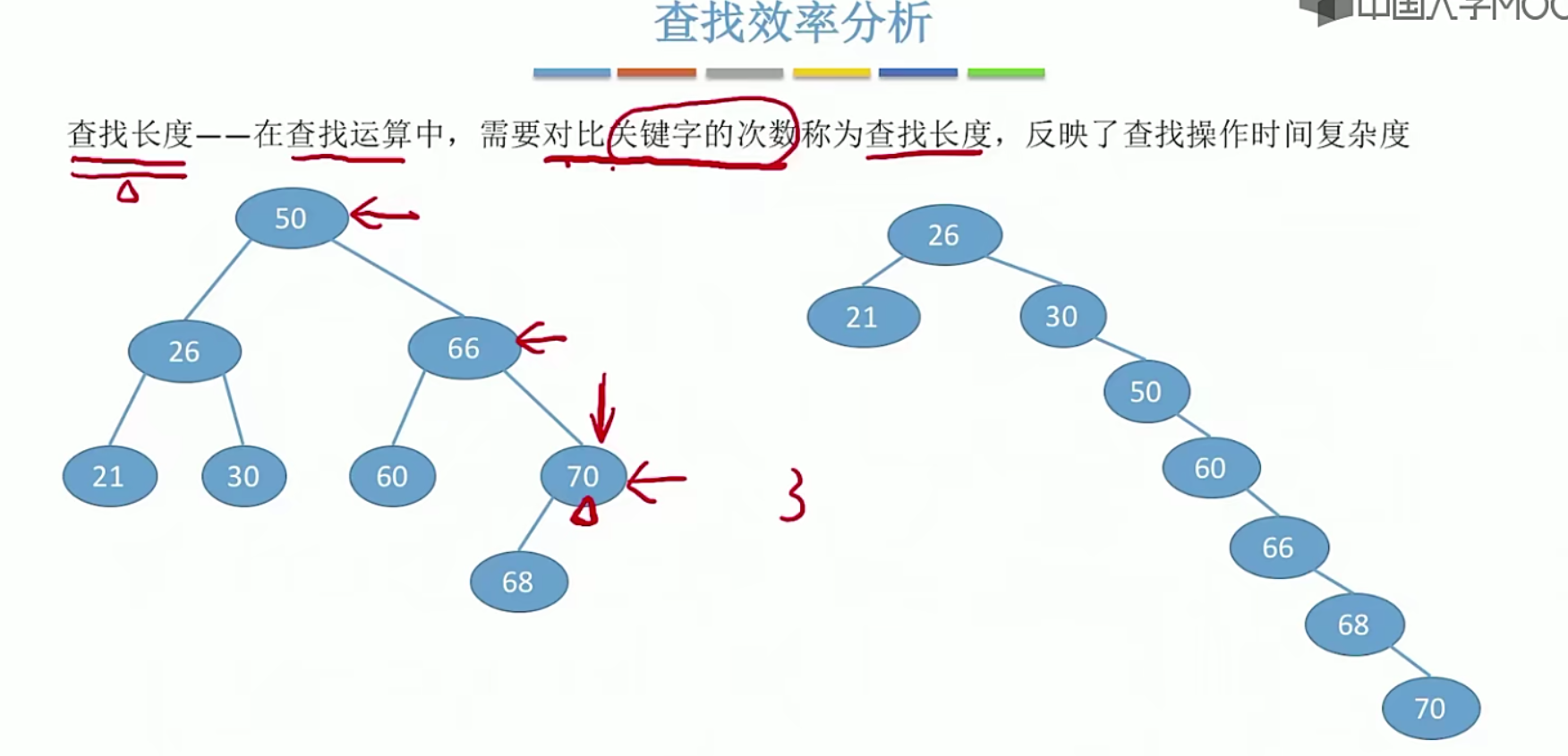
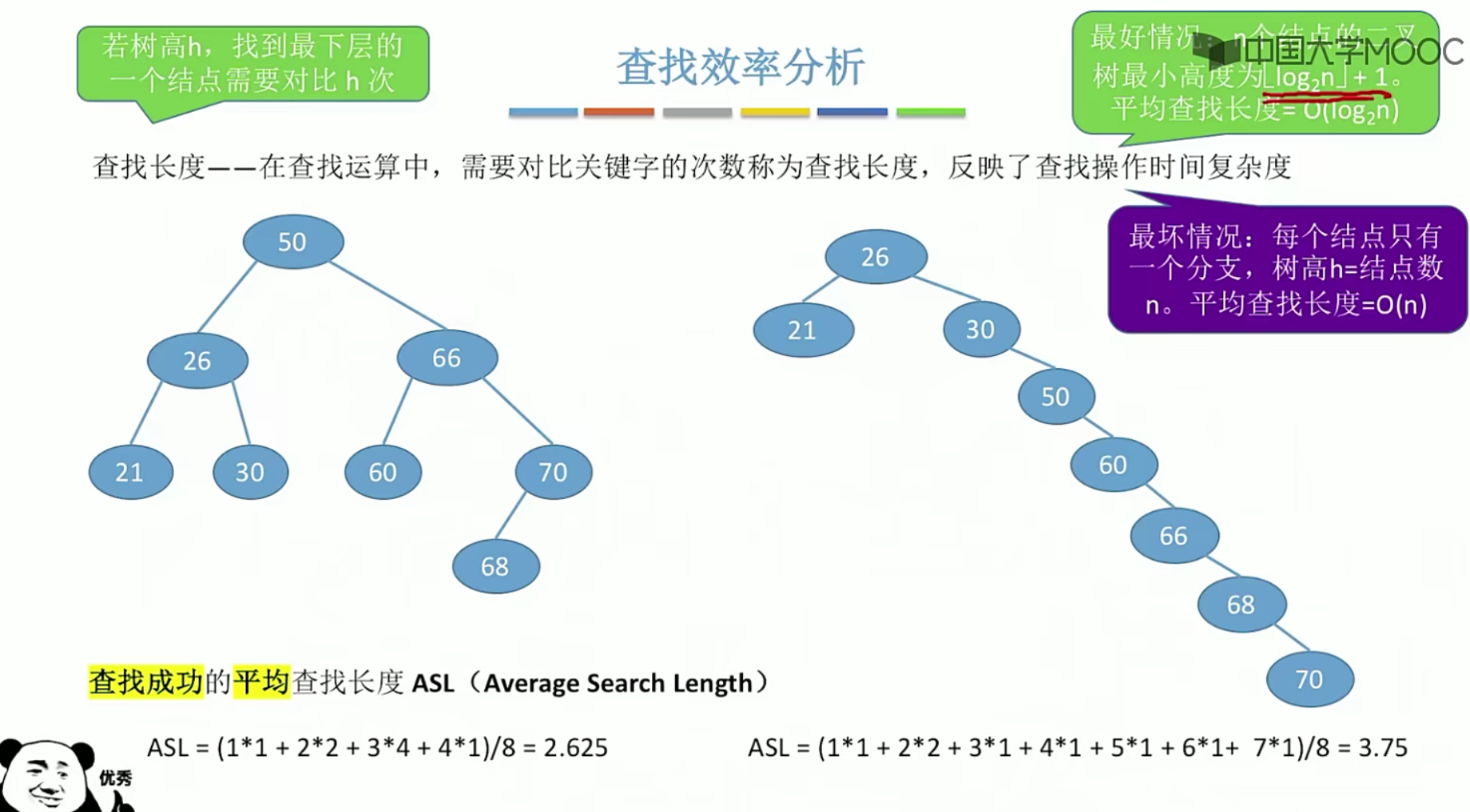
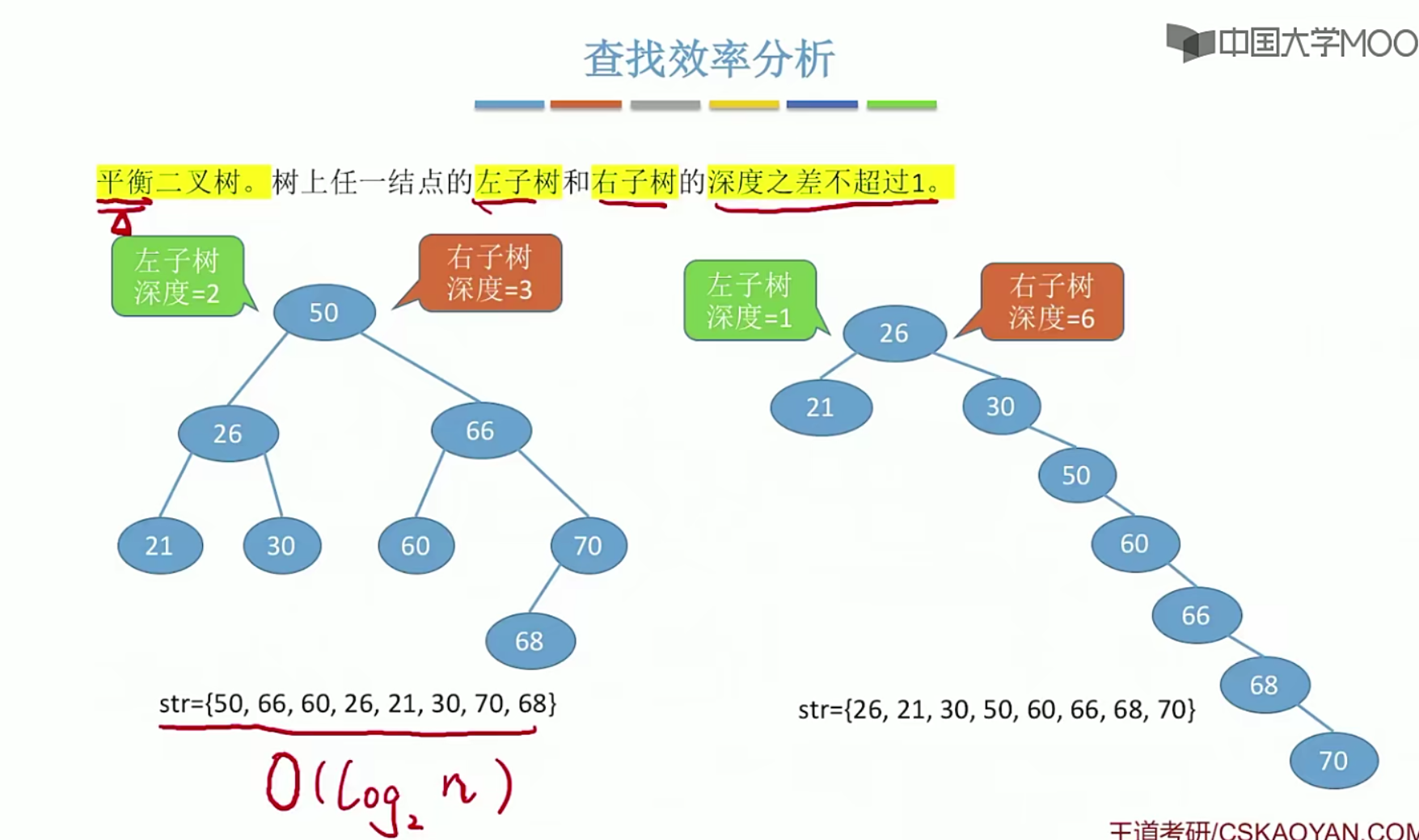
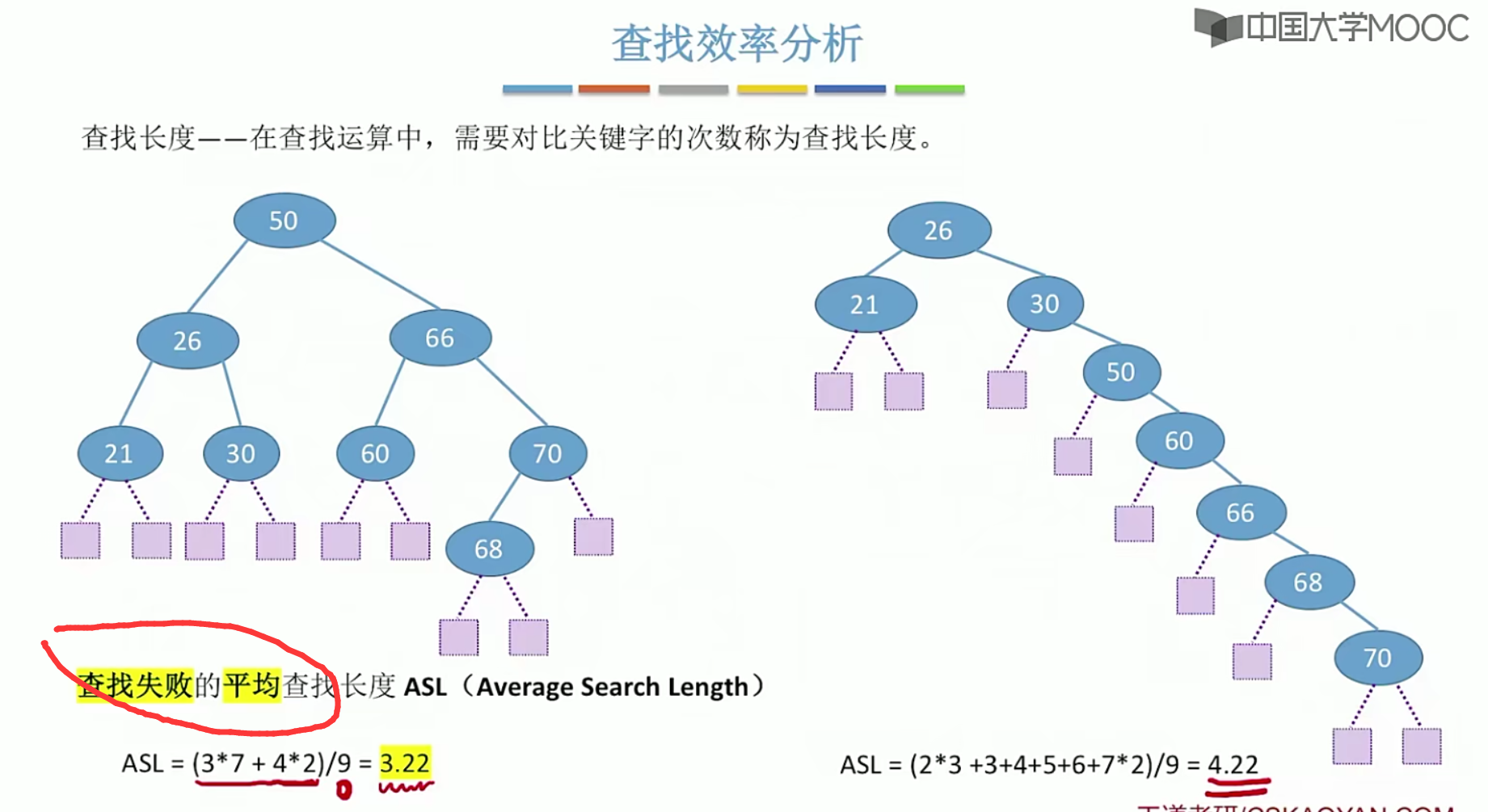
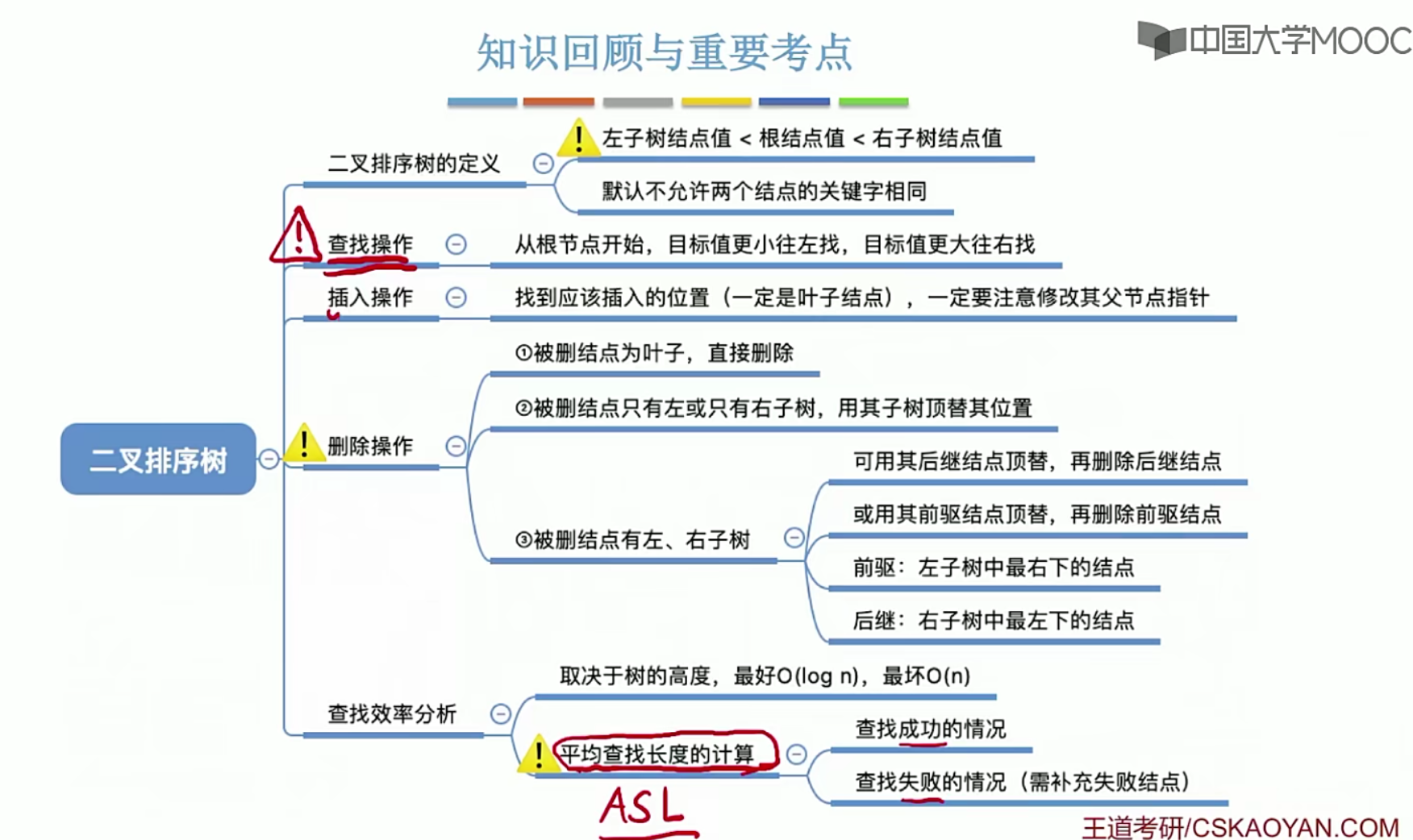
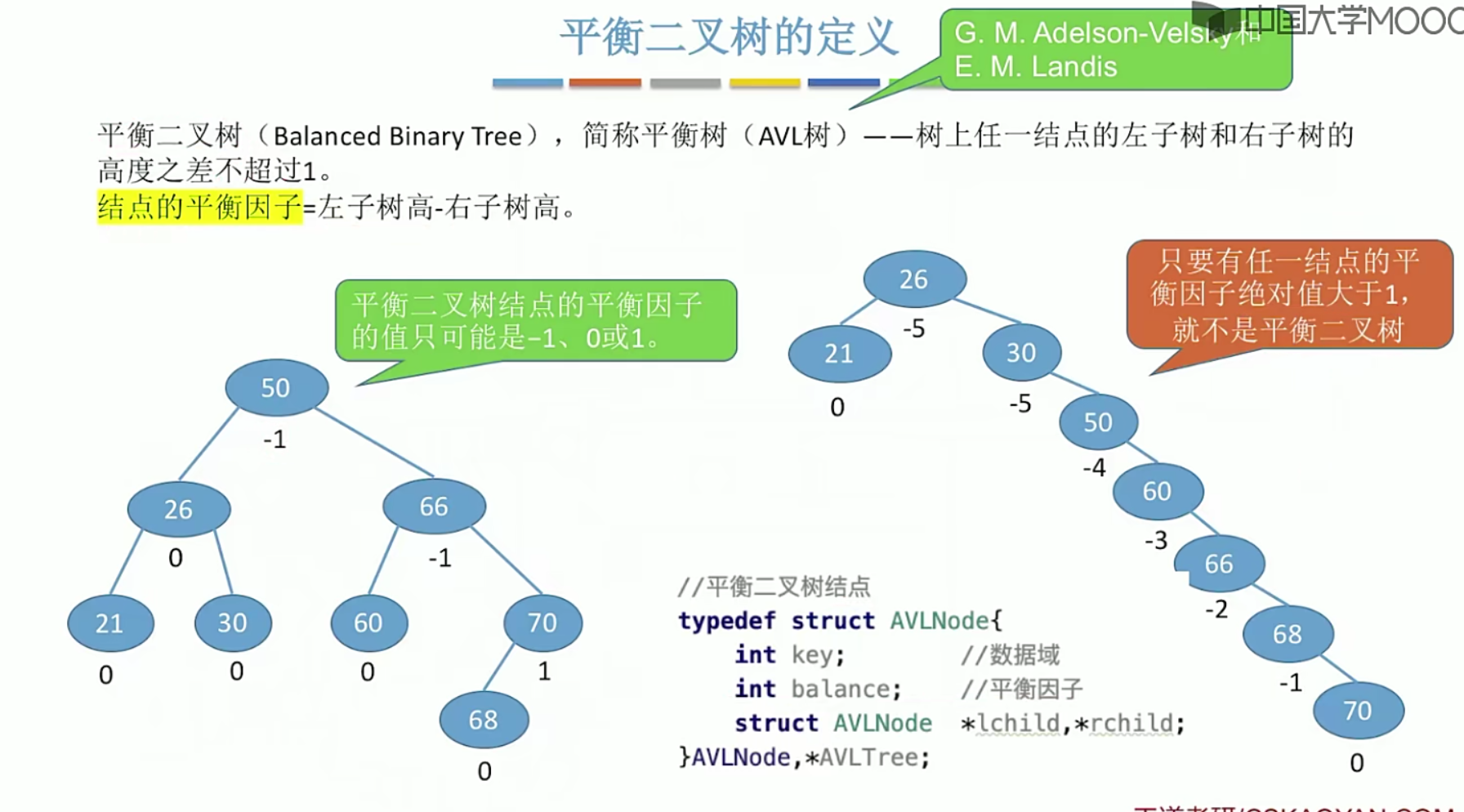
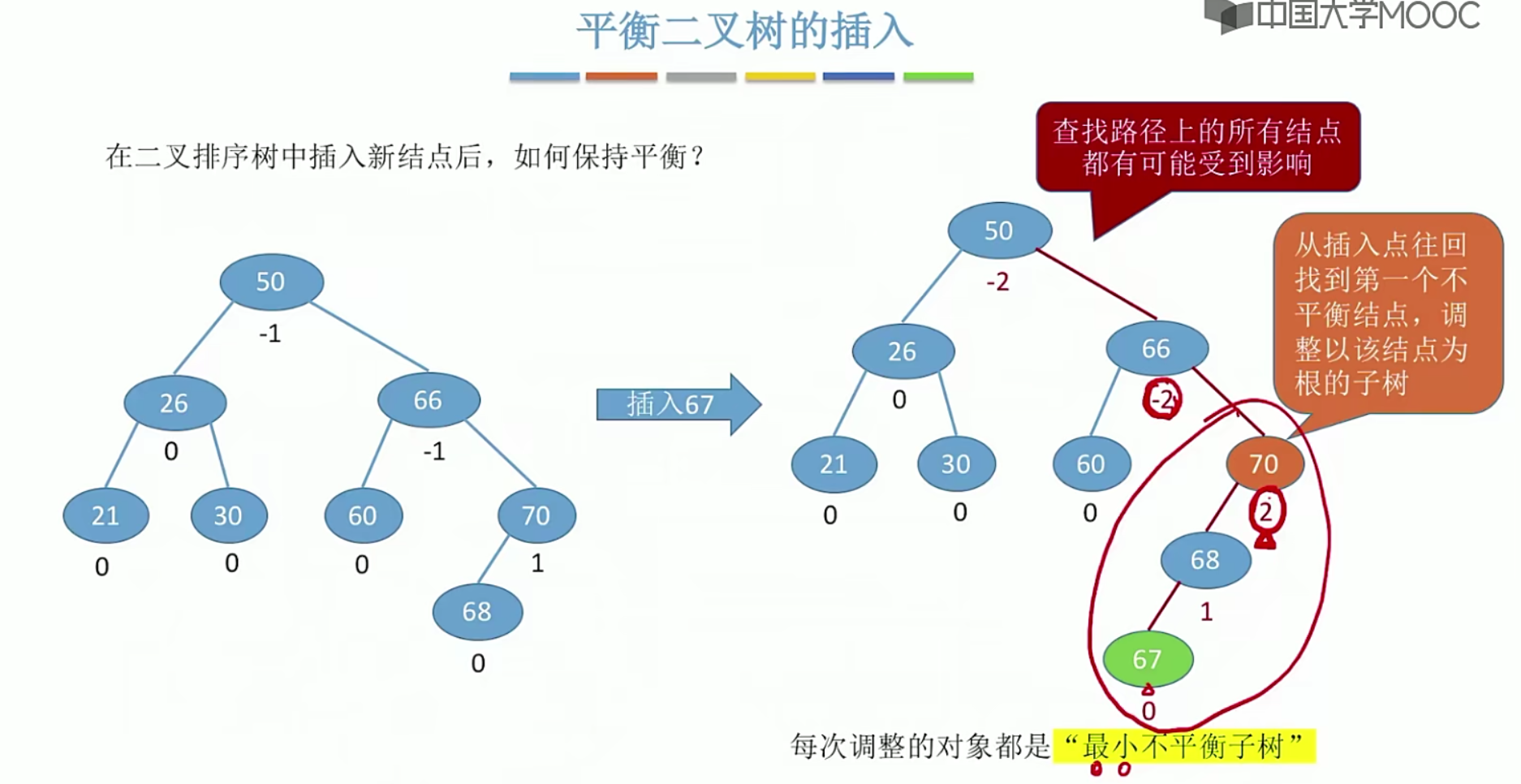
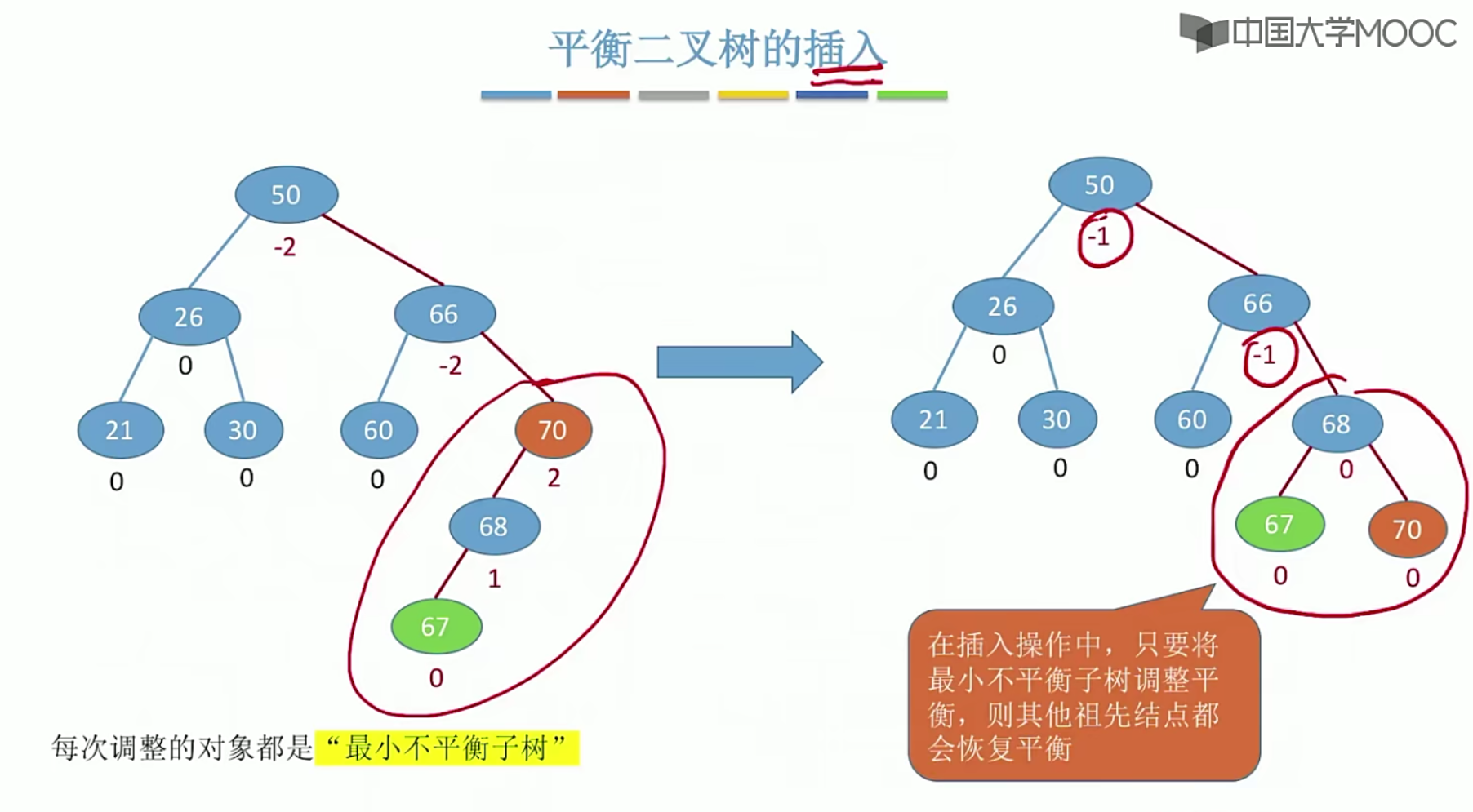
5.13平衡二叉树

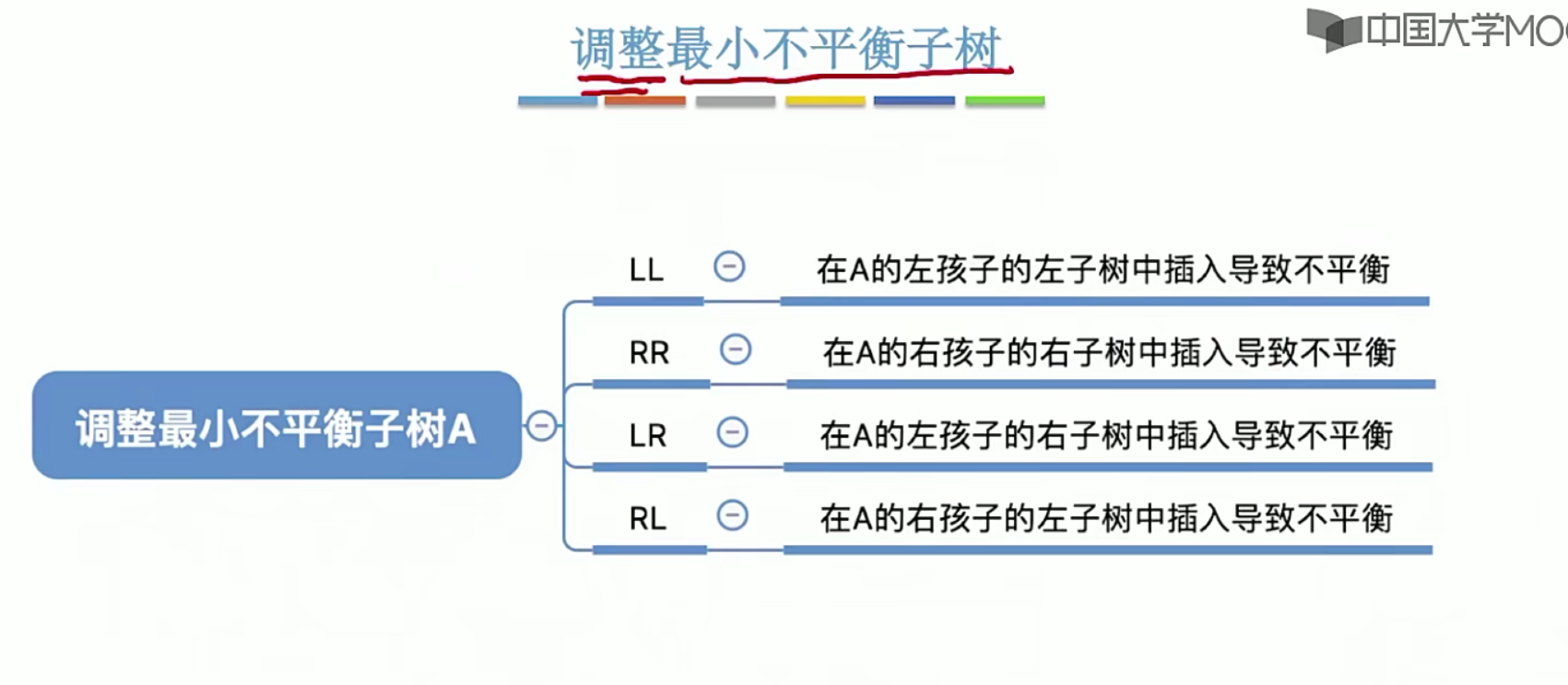
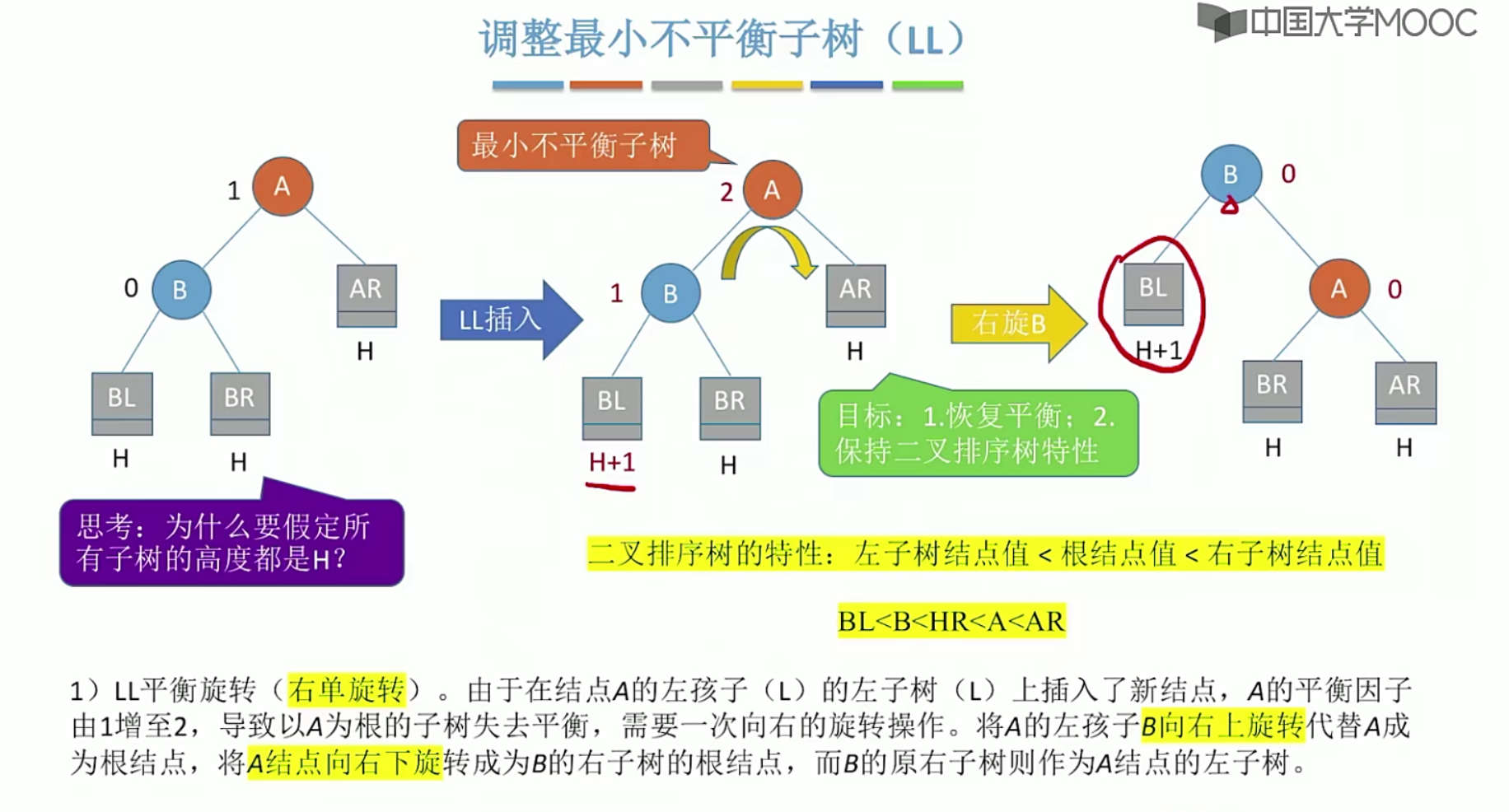
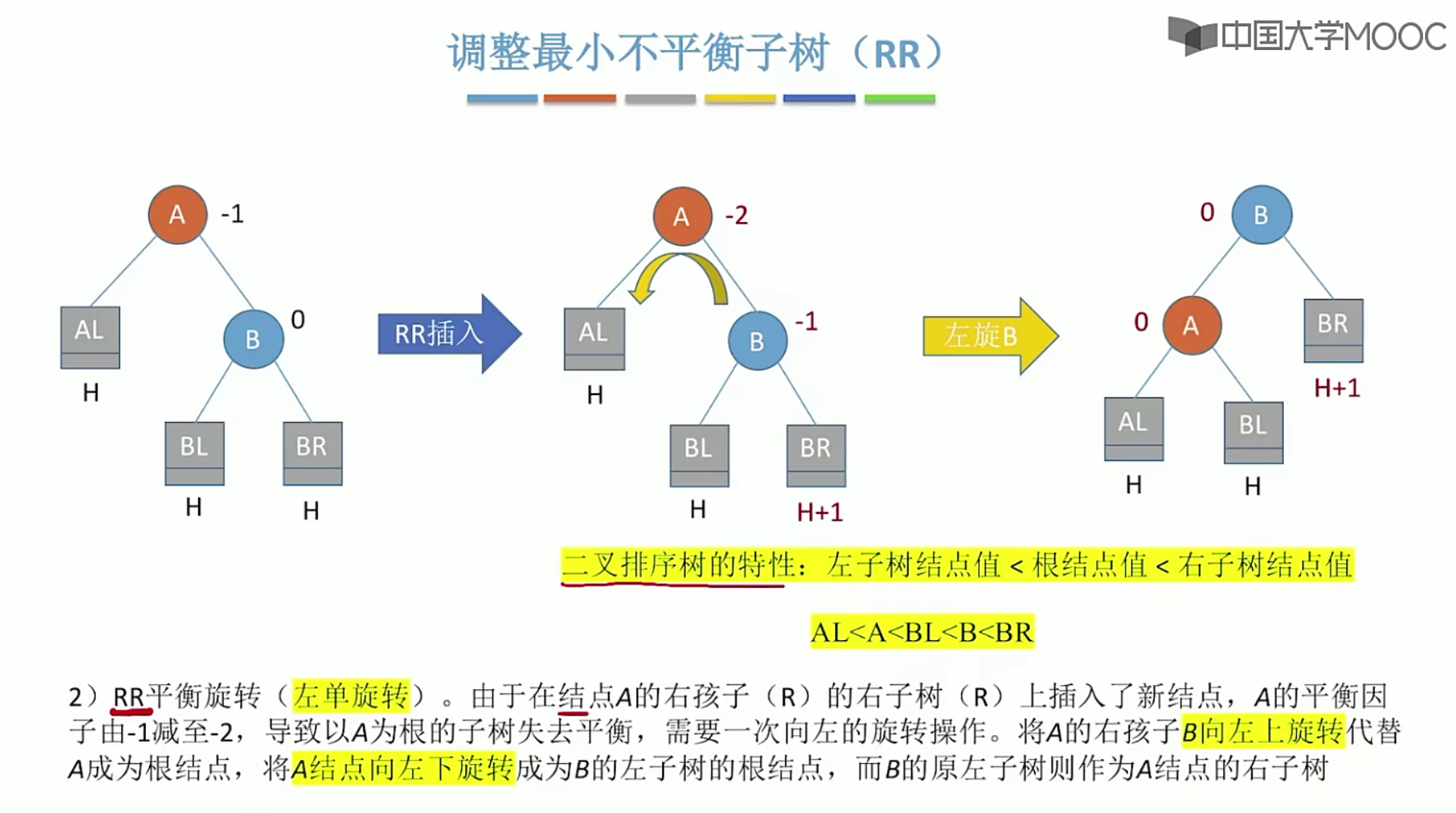
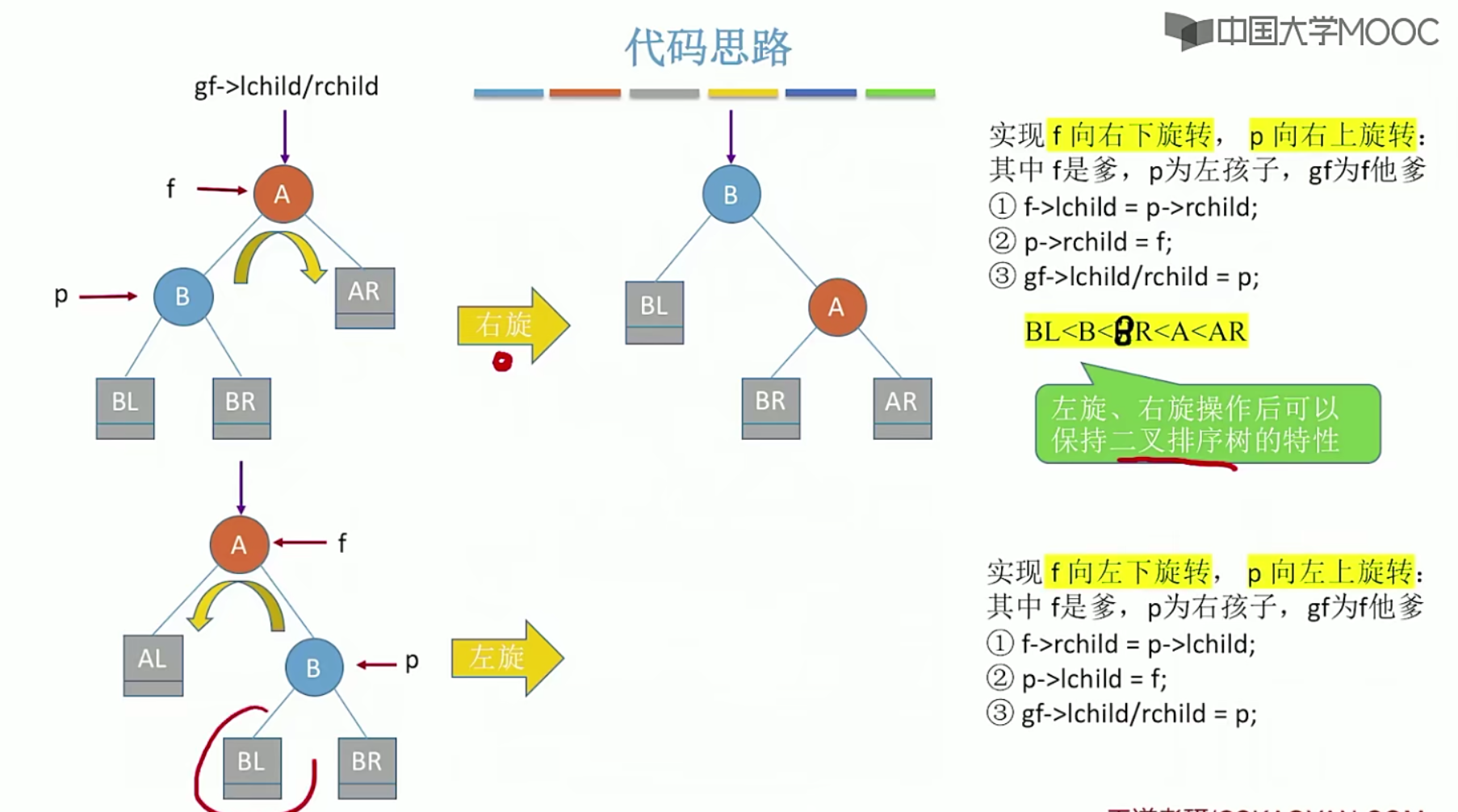
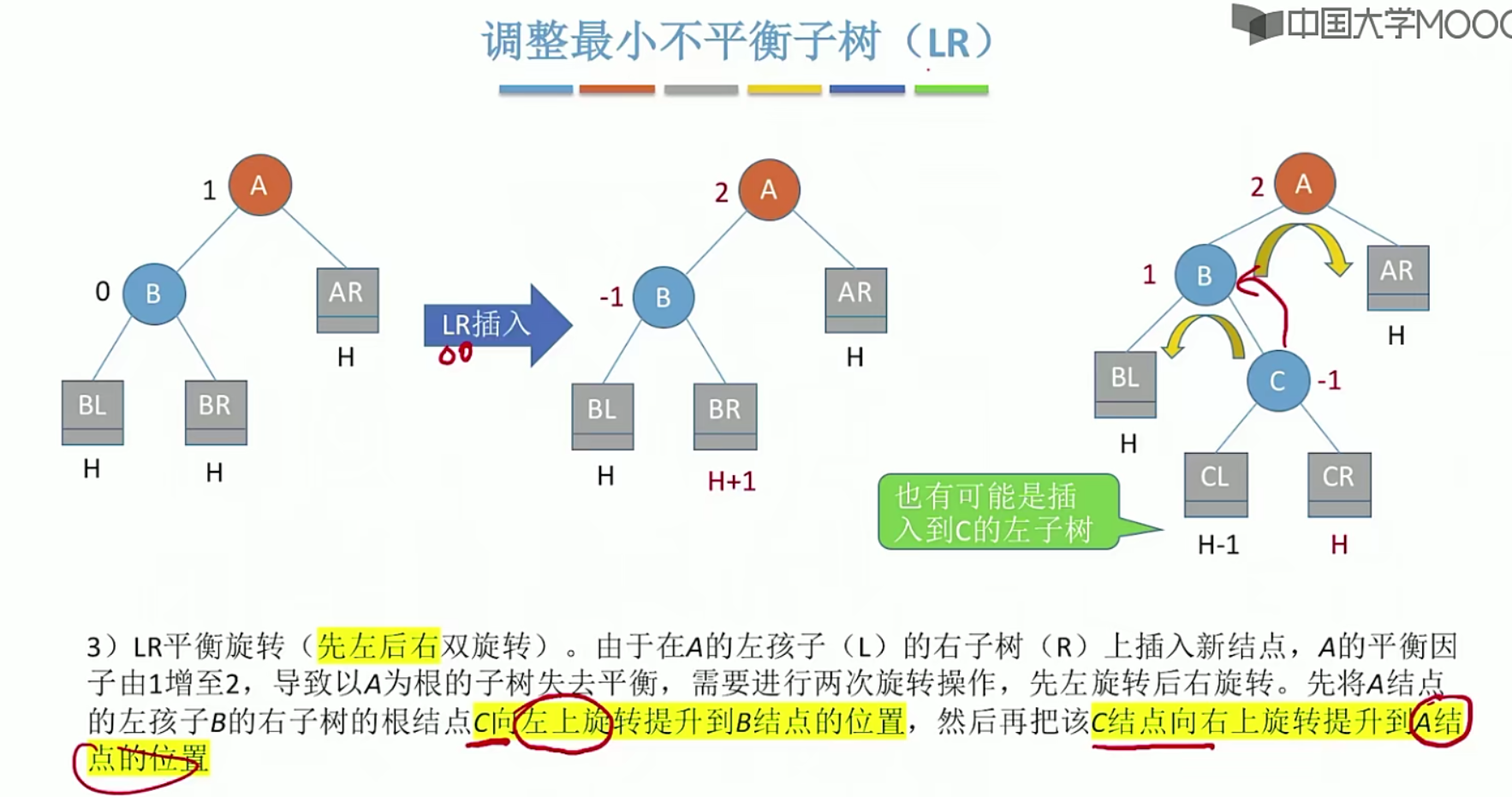
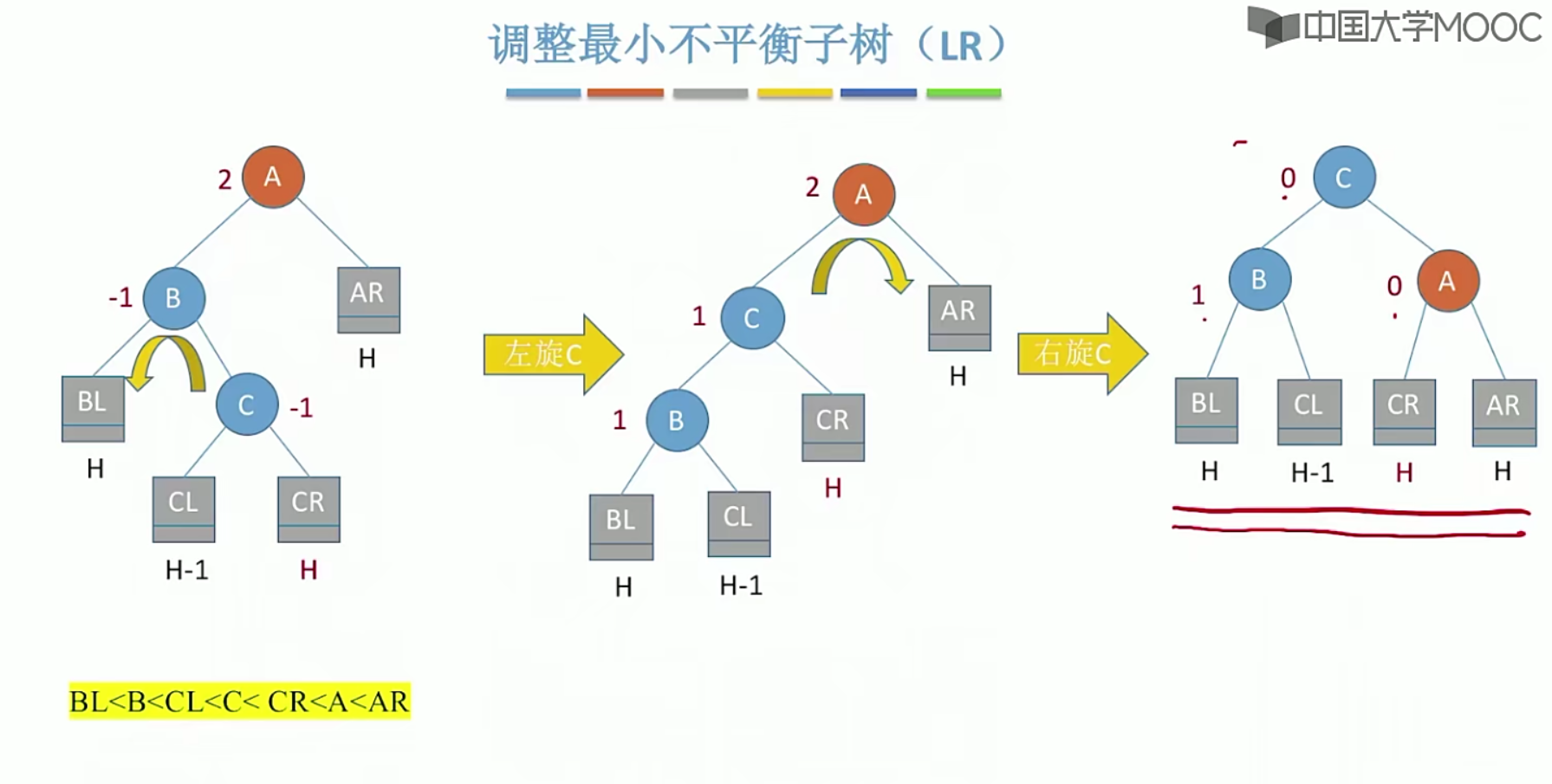
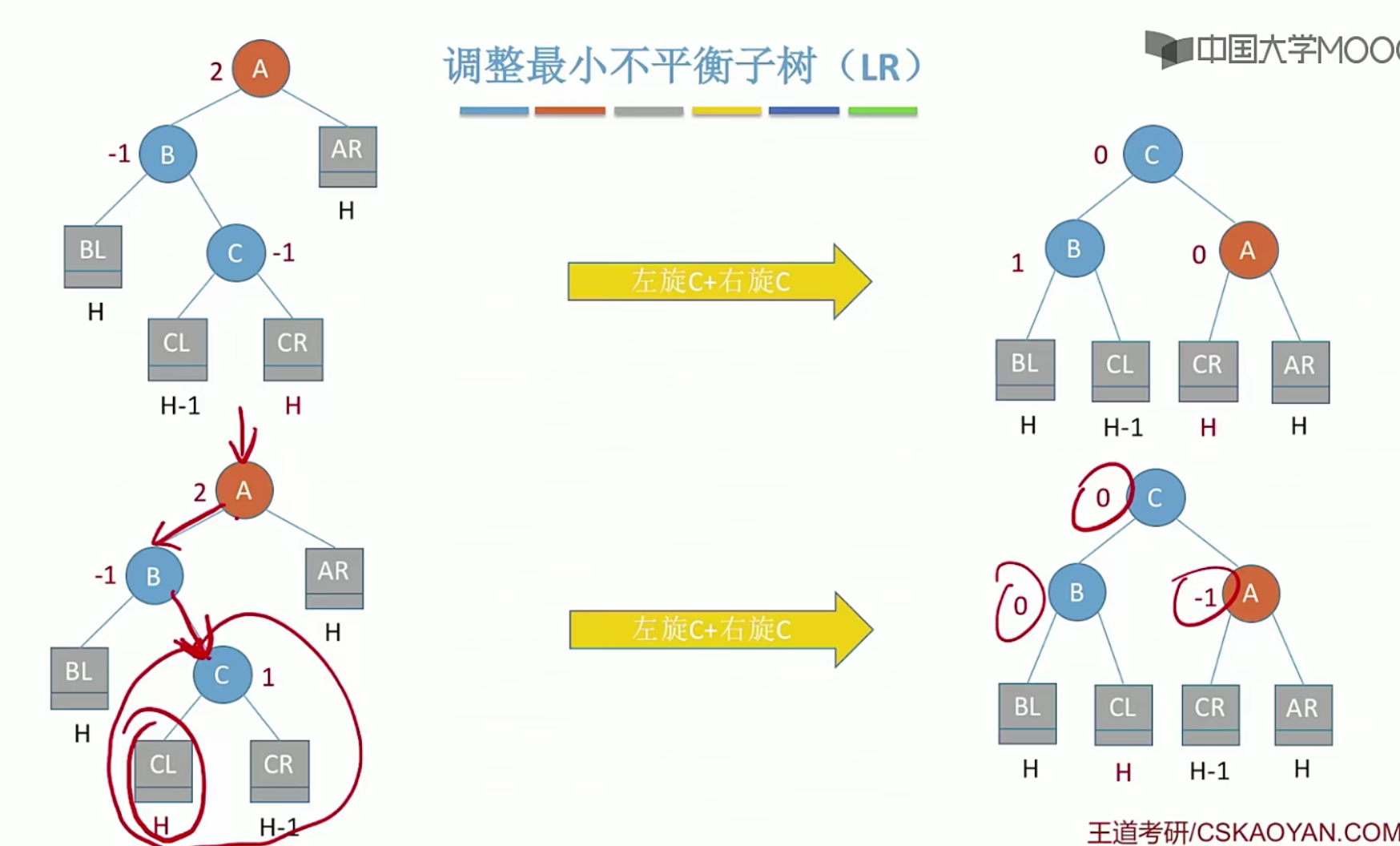
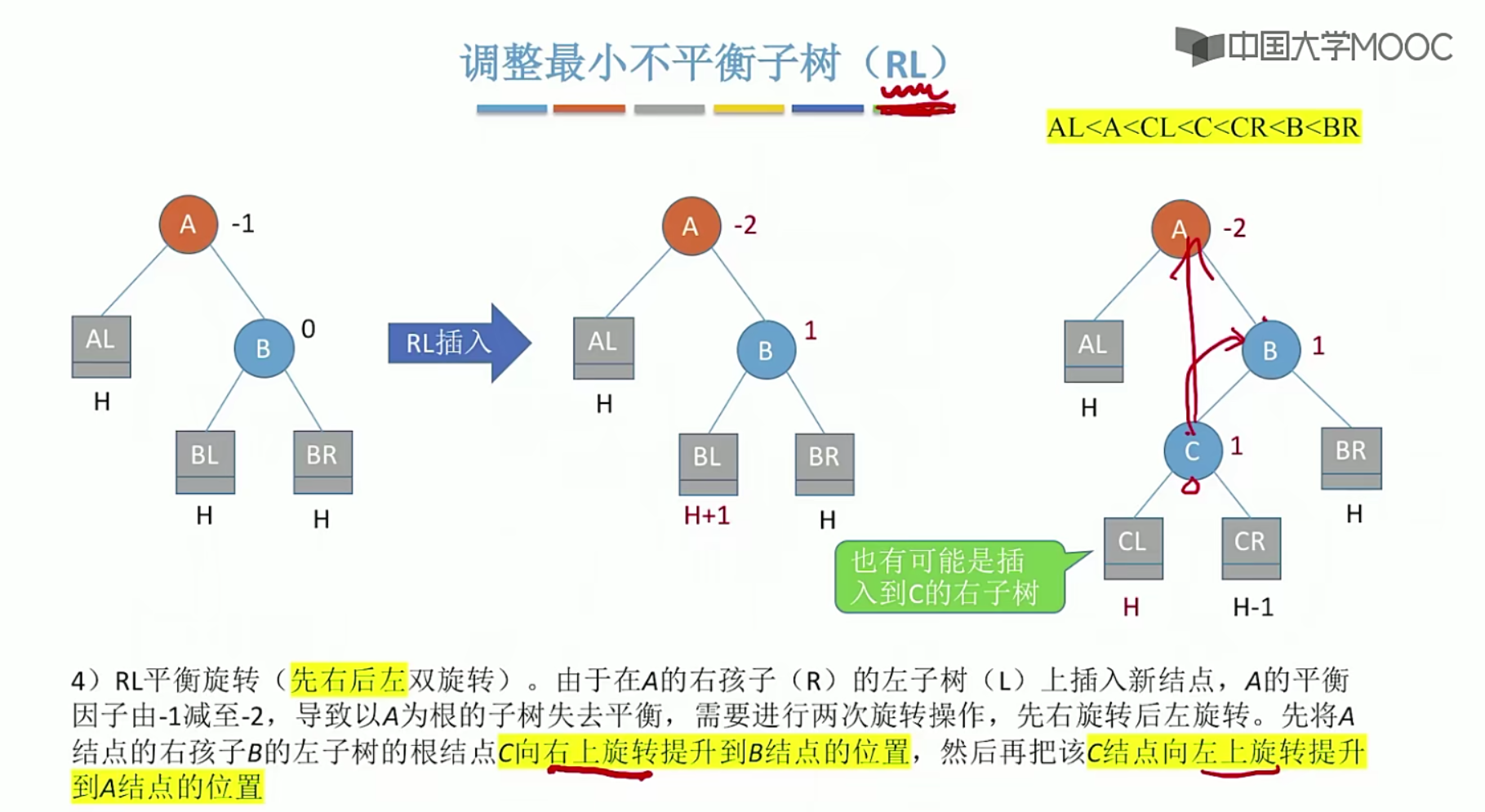
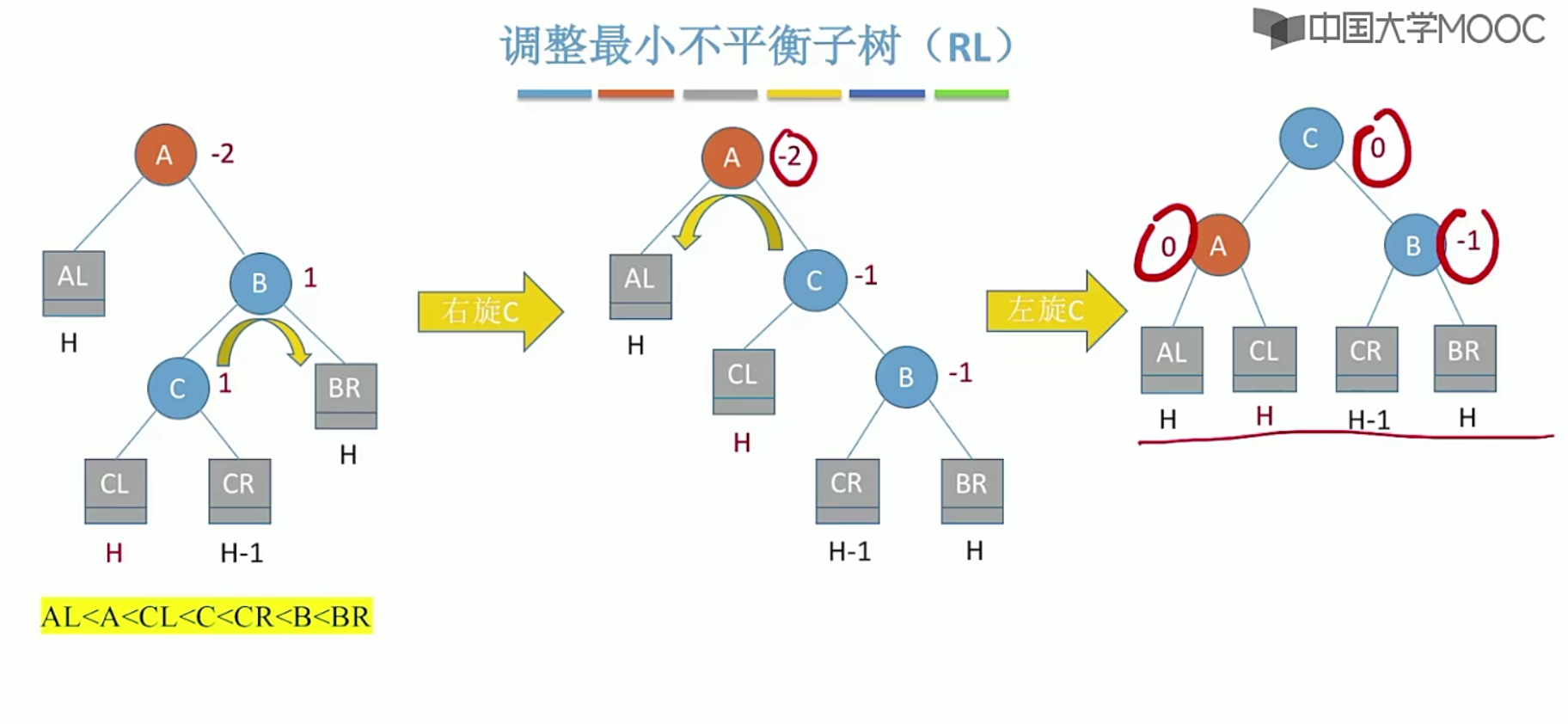
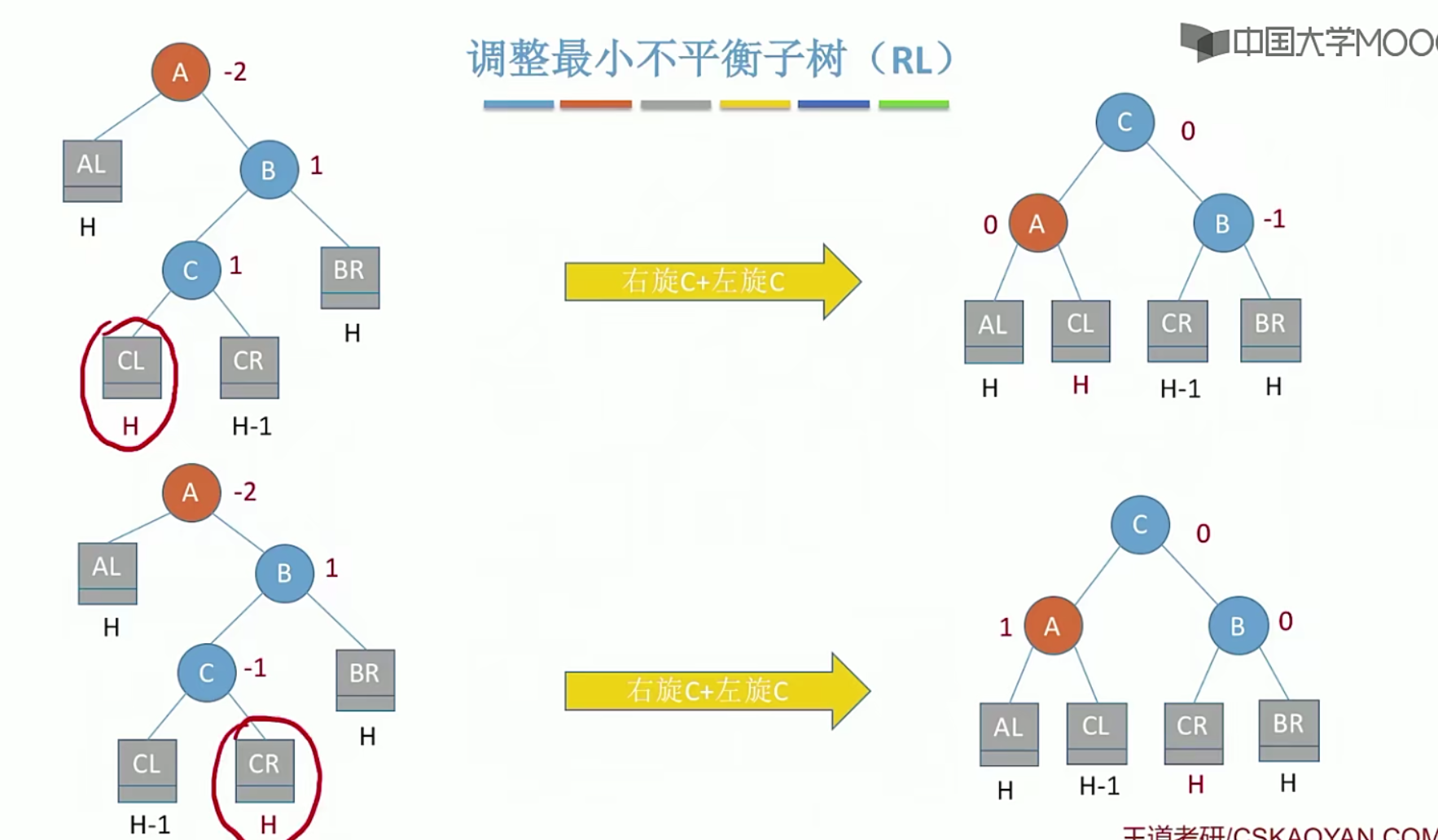
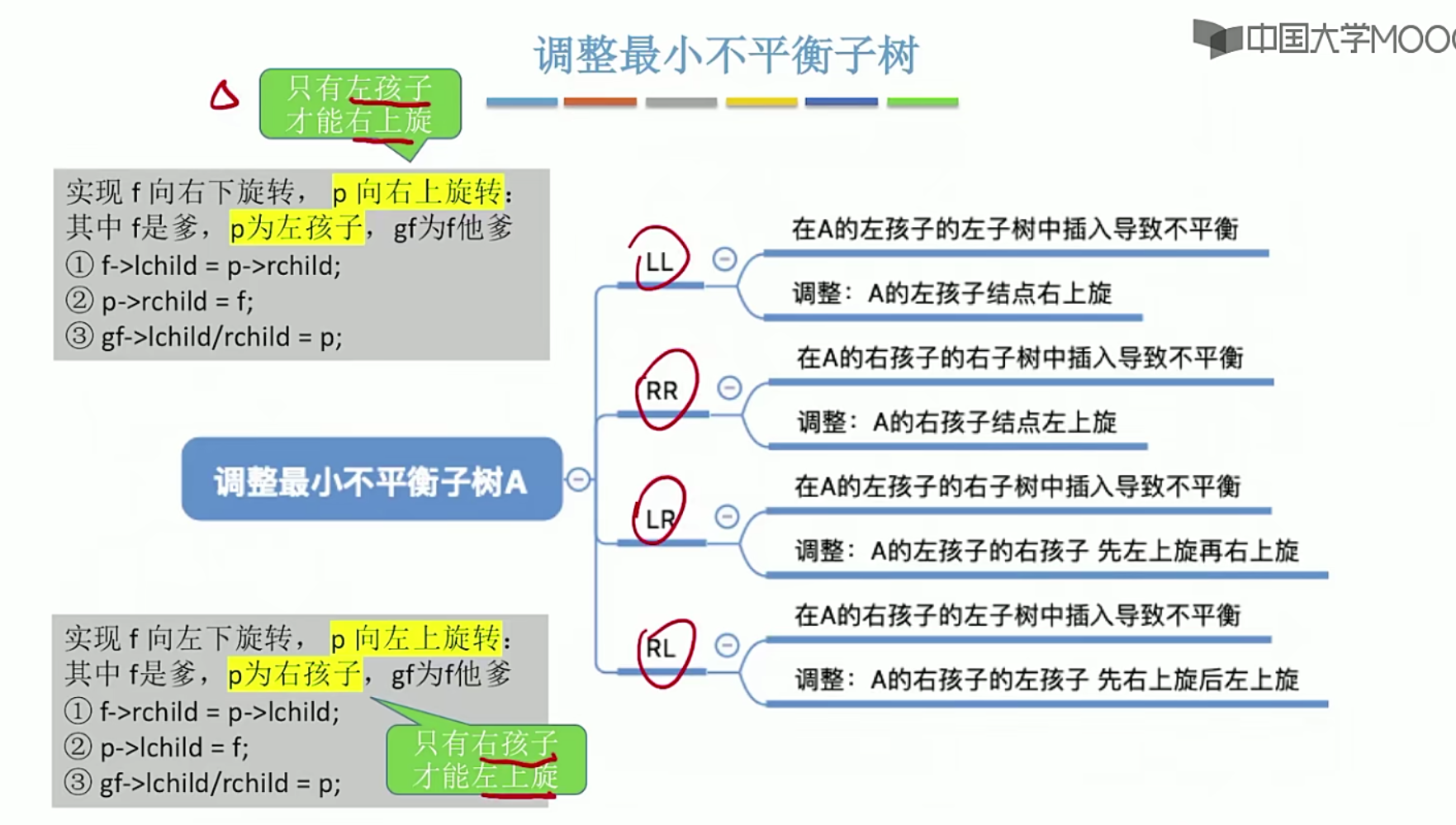
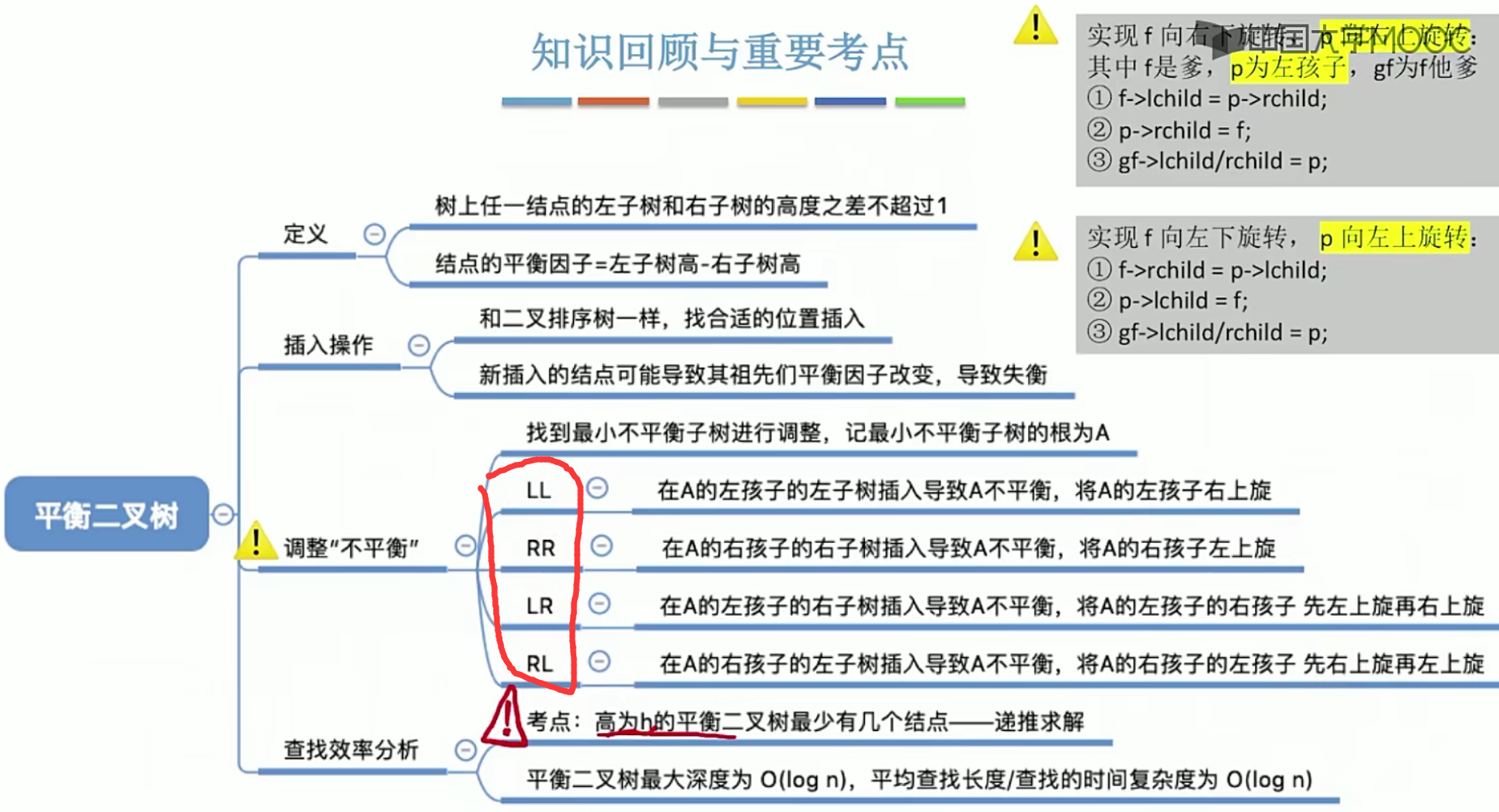
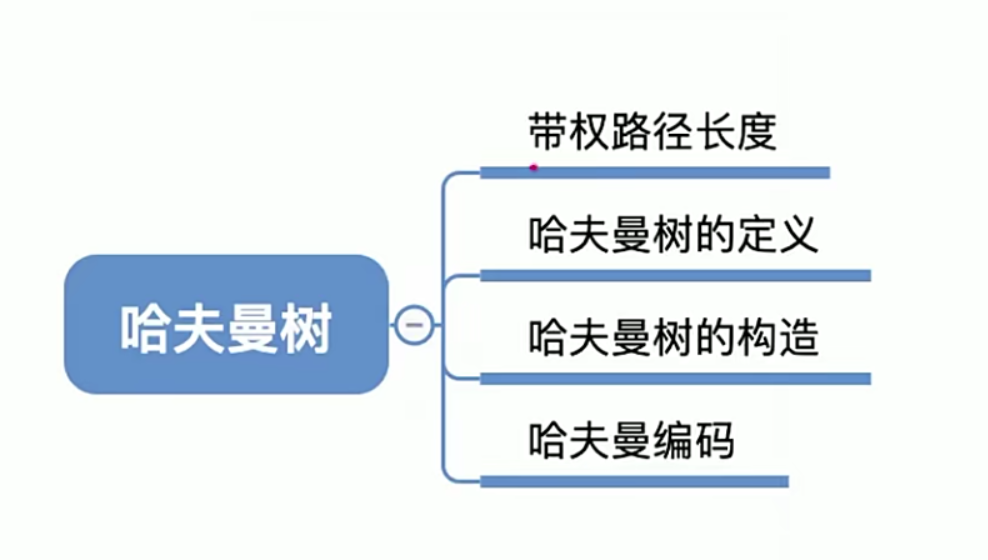
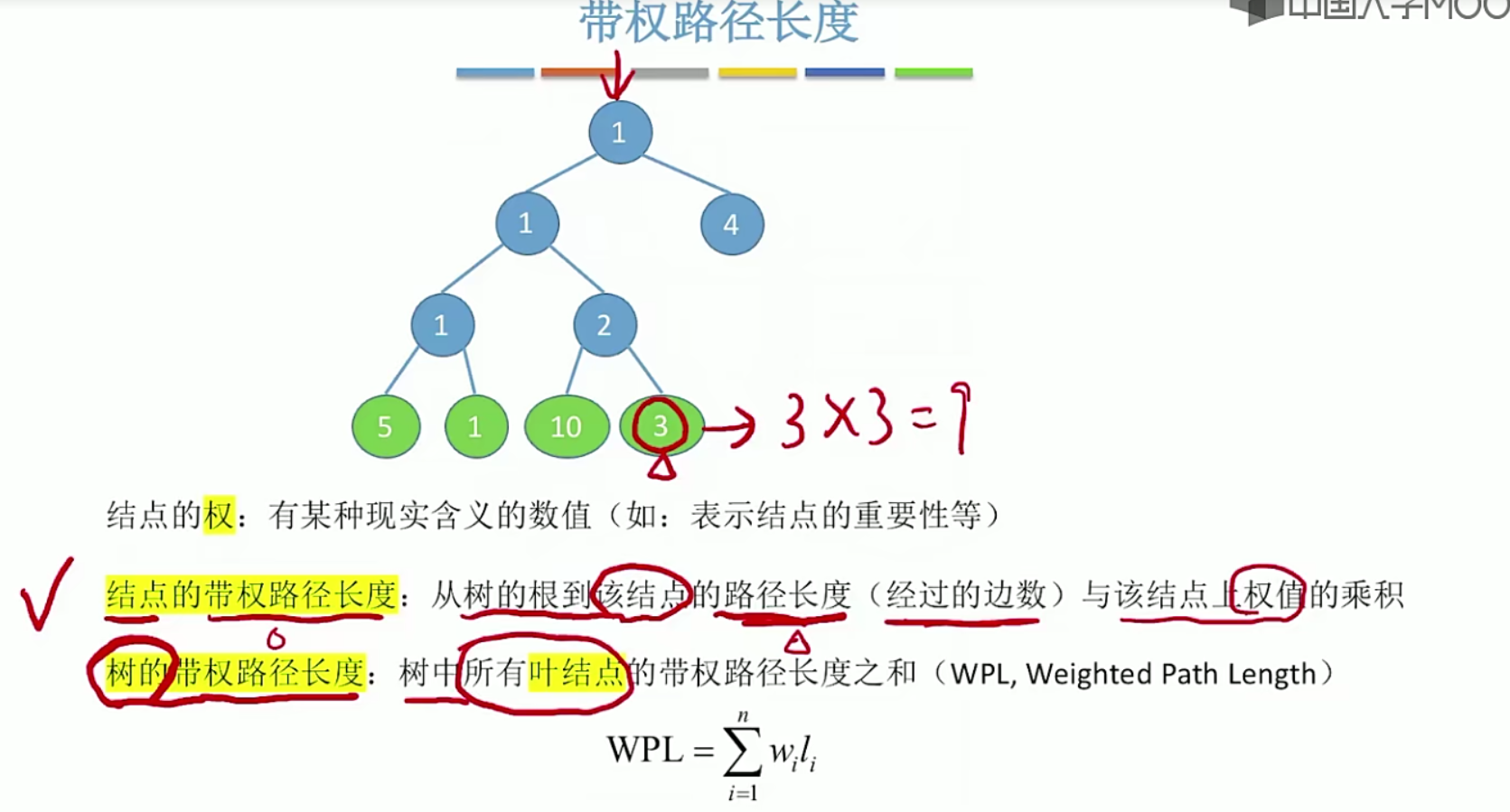
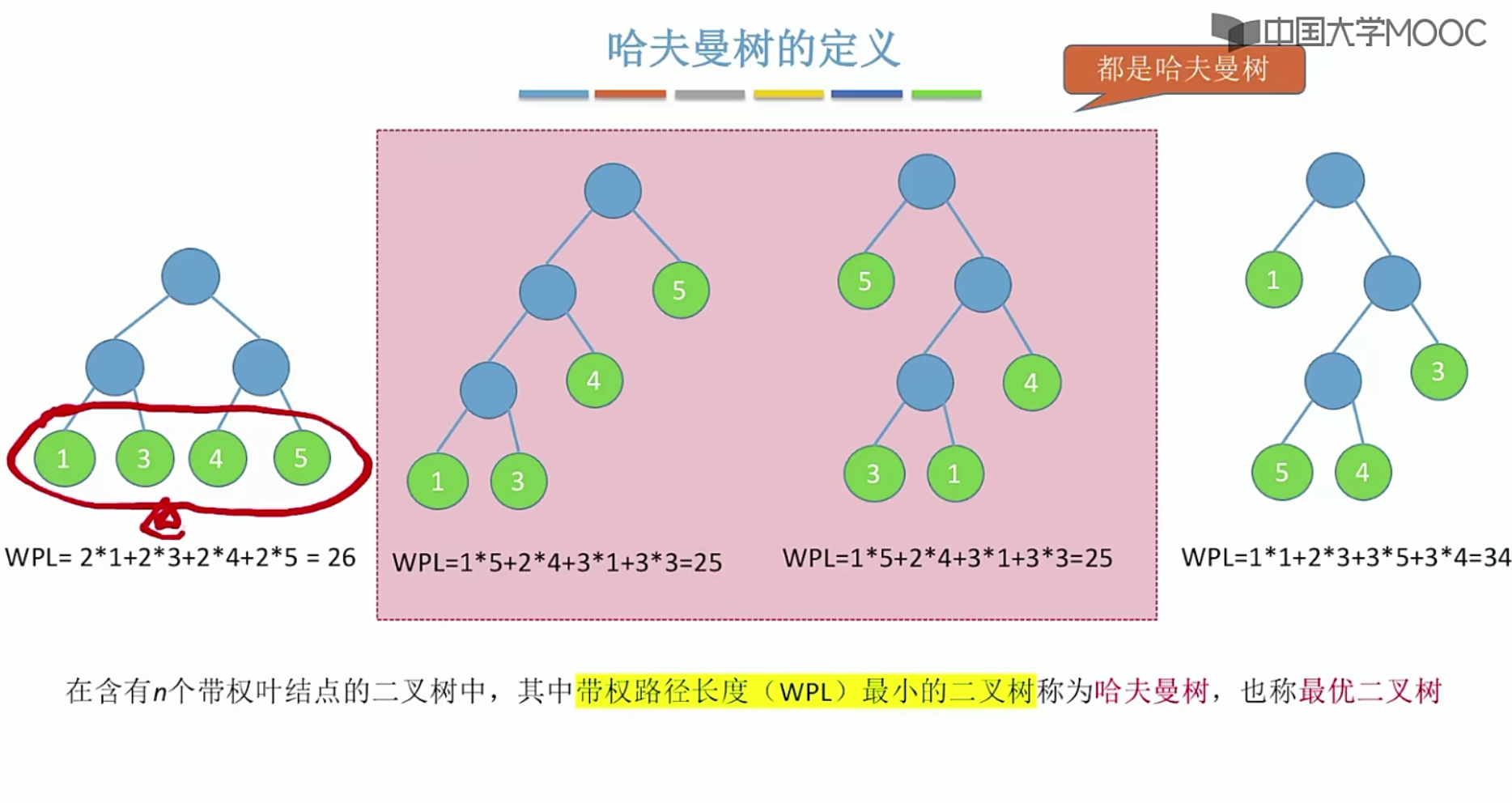
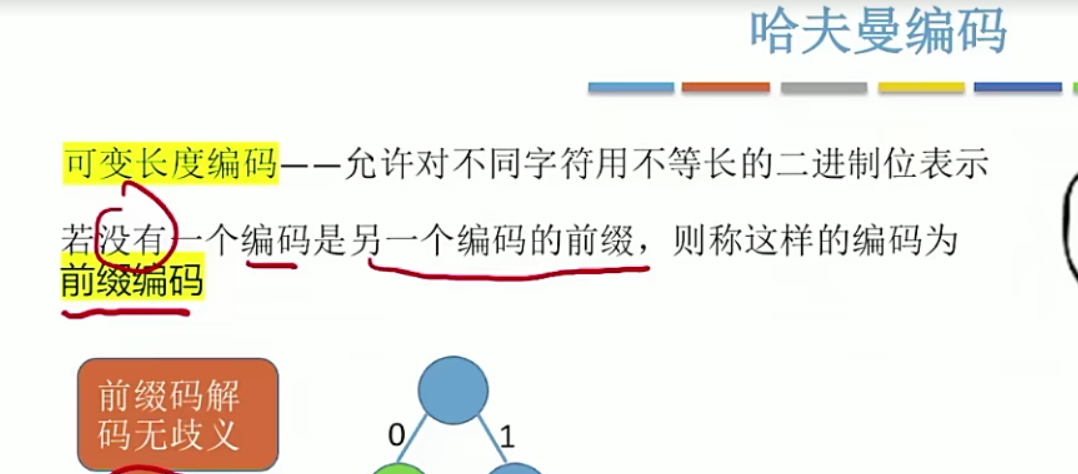
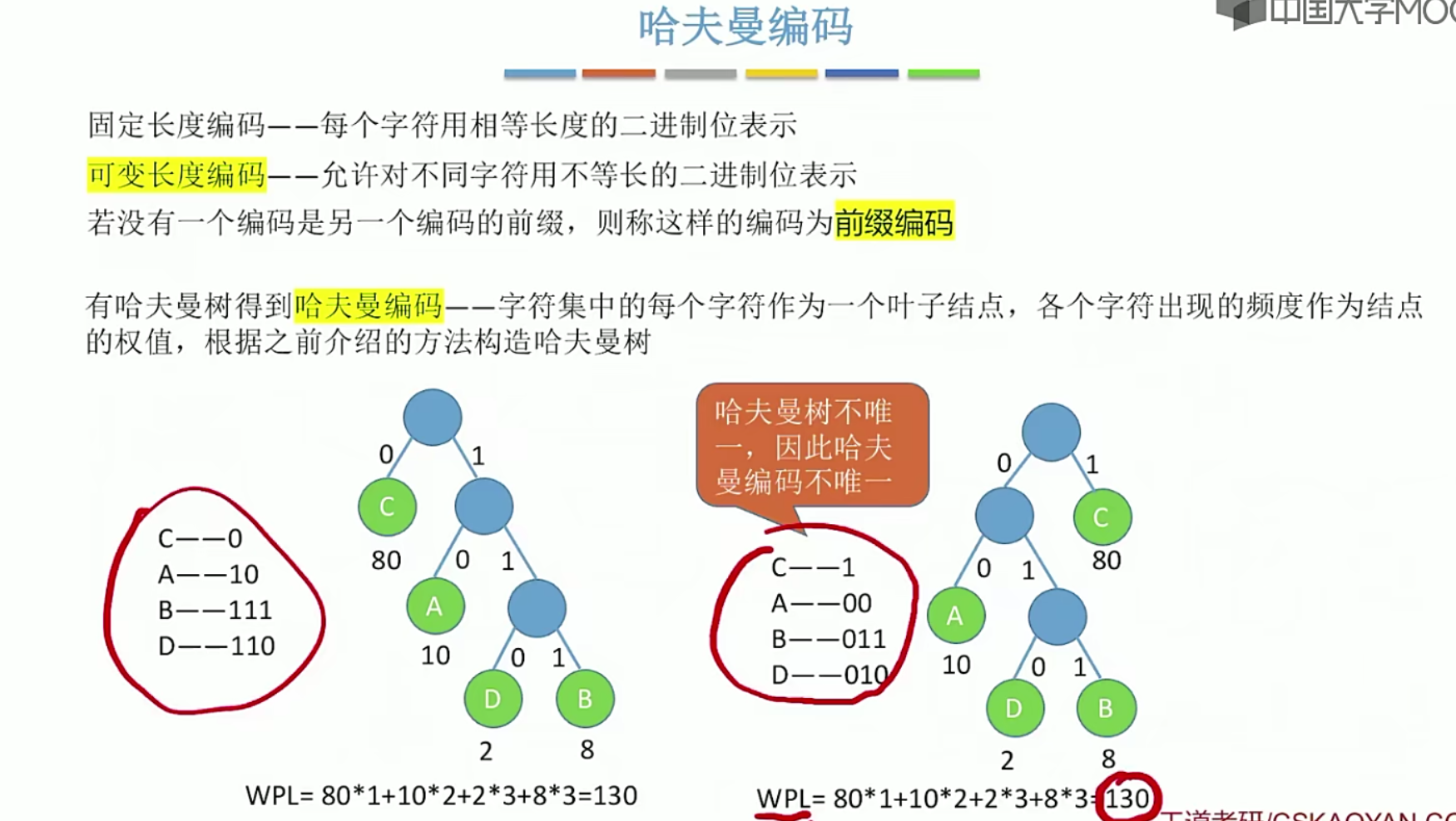
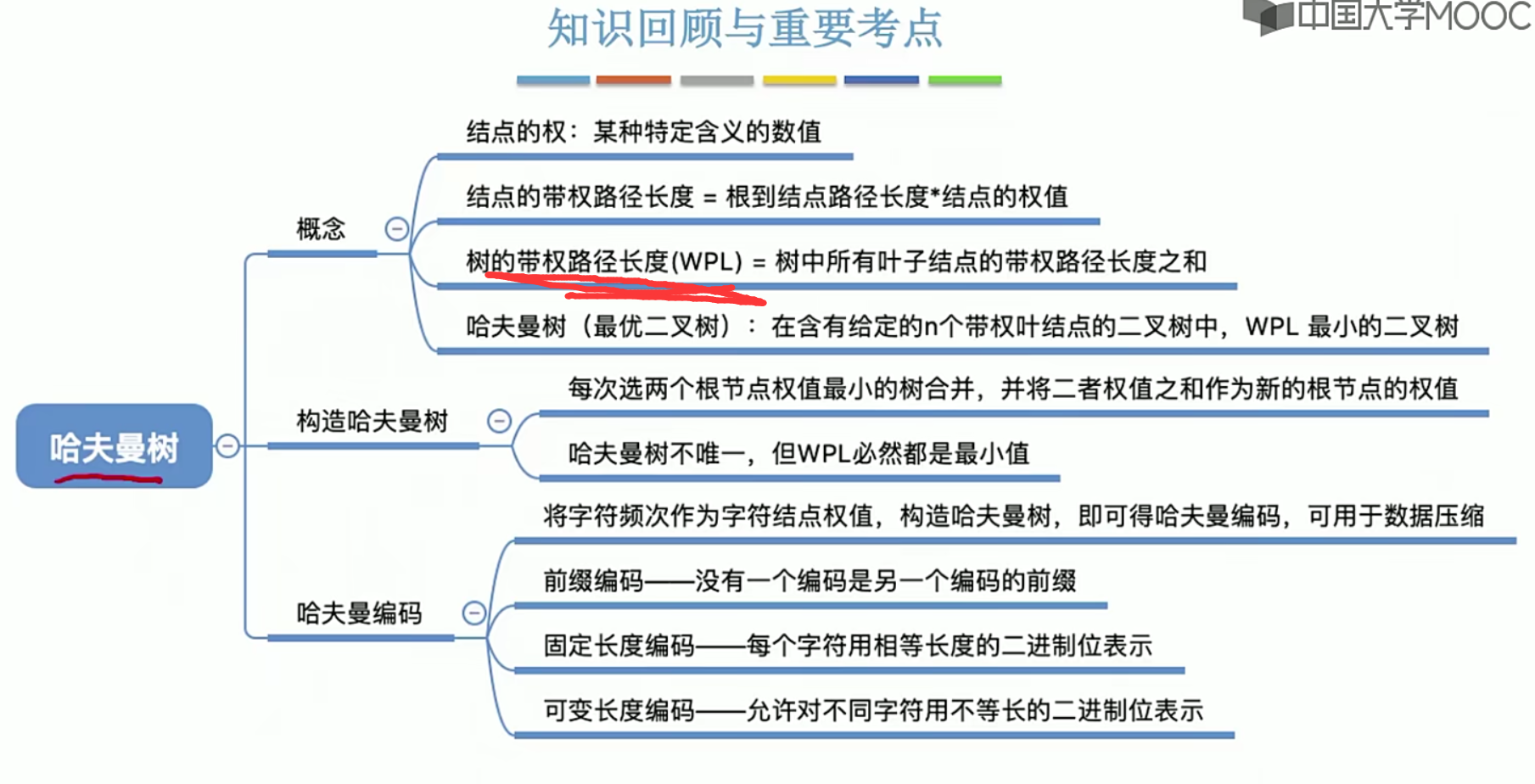
5.14 哈夫曼树