极化码之tal-vardy算法(1)
继前两节我们分别探讨了极化码的编码,以及深入到高斯信道探讨高斯近似法之后,我们来关注一个非常重要的极化码构造算法。这个算法并没有一个明确的名词,因此我们以两位发明者的名字将其命名为“Tal-Vardy算法”。
在《极化码小结(2)》之中,我们简单讲述了BEC信道下构造极化码的方法——通过直接计算巴氏参数Z(W)来构造,计算复杂度为O(N)。
在《极化码之高斯近似》中,我们讨论了常用的高斯信道下构造极化码的方法——高斯近似,计算复杂度也为O(N)。
现在,我们再次将极化码的触手伸向另一种常见的信道——二元对称无记忆信道(BMS)。
由于篇幅可能较大,因此我将分两节对该算法进行一个简略的介绍。我会将本文涉及到的参考文献放在相关内容开头,并建议有需要的各位去读原论文。
【1】《How to Construct Polar Codes》Ido Tal, Alexander Vardy.
Part1. 简单介绍
这套算法中,有两个核心的信道操作,一种叫做信道弱化(degrade),另一种叫做信道强化(upgrade)。论文作者形象的将这两种操作产生的弱化信道、强化信道与原信道的关系比喻成“三明治”的结构。
 图1 三种信道之间的关系示意
图1 三种信道之间的关系示意
论文的大致思路,就是通过将原始信道通过弱化操作和强化操作,使之成为弱化信道和强化信道。分析发现,这两种信道在各种参数水平上都极为接近,因此通过类似数学上的“两边夹定理”,我们可以用这两个信道来近似原始信道。
“tal-vardy算法”构造极化码的思路是直接计算各信道的错误概率Pe(W),然后利用这个参数来挑选我们所需的信息位。这种挑选信道的方法显然更具有普遍性。。“Tal-Vardy算法”是针对B-DMC(二元离散无记忆)信道提出的,对于像高斯信道这样具有连续输出的信道不能直接使用。因此作者也提出了一种办法,使得这种算法同样能够应用于输出连续的信道。
我们之前提到过,计算信道错误概率Pe(W)的难度在于W的输出符号集大小随着n呈指数型增长,这是需要克服的难点。为了使上述计算成为可能,作者在弱化操作或强化操作中,通过使用“合并函数”,使得输出符号集能够缩减到指定的符号集大小。
利用该算法构造极化码的时间复杂度为n的线性复杂度。
根据论文的思路,为了更好的理解这篇论文中所提出的这一算法,我们将尝试从三个部分来探讨。分别是输出字符集的合并、信道操作、如何处理连续对称信道。
Part2.研究对象
【2】《A Note on Symmetric Discrete Memoryless Channels》Ingmar Land.
在研究极化码构造问题时,我们经常遇到各种各样的信道,现在我们来做一个简单的总结。
DMC(离散无记忆信道)
DMC具有离散的输入字符集X,离散的输出字符集Y,以及转移概率函数P(y|x)。它的输出仅仅与当前的输入有关,因此它又是无记忆信道。
假设输入字符集大小为Mx,输出为My,不失一般性的,我们假设:
那么,这个 信道的转移概率可以用一个矩阵来表示:
注意到,矩阵的每一行的和都为1。
Strongly Symmetric DMCs(强对称DMC)
在介绍这个信道之前,我们先来介绍一个概念——恒等排列。
如果向量v和向量μ中的元素完全相同,只是元素的排列顺序不同,那么,我们称v为μ的一个恒等排列。
eg. μ=[1 2 3 4],v=[2 4 1 3],则v是μ的一个恒等排列。
定义:对于一个信道的转移概率矩阵,如果矩阵的每一行都是其他行的恒等排列;每一列都是其他列的恒等排列,那么我们称这个转移概率矩阵所描述的DMC为“强对称DMC”。
一个非常特殊的例子是二元对称信道(BSC):
图2 二元对称信道
二元对称信道的输入字符集为{0,1},输出也为{0,1},其转移概率矩阵为:
对称DMC
定义:对于一个转移概率矩阵,如果它能够按列拆分为数个子矩阵,使得每一个子矩阵都满足“强对称”定义,那么,我们称这个转移概率矩阵所描述的DMC为“对称DMC”。
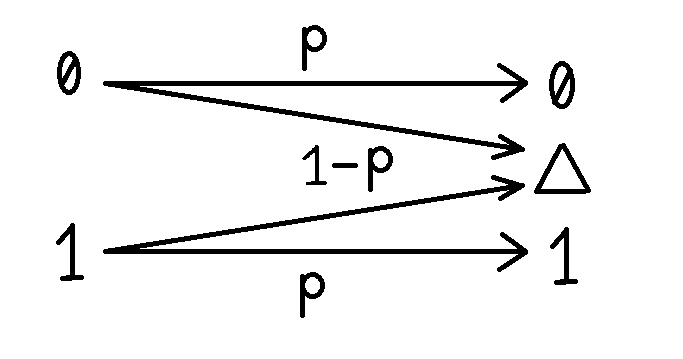
一个特殊的例子是二元删除信道(BEC):
图3 二元删除信道
它的输入字符集为{0,1},输出字符集为{0,△,1},其中△为删除符号。BEC的转移概率为:
显然 ,它可以按列拆分为两个子矩阵:
这两个矩阵都符合强对称信道的定义,因此BEC是对称DMC。
另外一个特例是AWGN信道。BPSK调制下,AWGN信道的输入字符集为{-1,1}。首先,可以用相对于y = 0对称的量化区间来量化输出(也即,将连续输出近似为离散输出),它的子信道都是BSC,根据上述定义,所生成的信道是对称的。其次,这个量化区间可以设置的无穷小,其子信道依旧是BSC,不过子信道的数量趋近于无穷。
弱对称DMC
定义: 对于一个转移概率矩阵,如果它的每一行都是其它行的恒等排列,且每一列之和都是相等的,那么,我们称这个转移概率矩阵所描述的DMC为弱对称DMC。
eg.给定一个弱对称DMC,其输入字符集为{0,1}(注意,这个地方在【2】中错写为{0,1,2}),输出字符集为{0,1,2},其转移概率矩阵如下:
如果一个信道的输出符号集为{0,1},那么我们称这个信道有二元输入,“二元输入的对称无记忆信道”,这就是本文中的算法所研究的对象。我们来简单了解一下它的性质。
Arikan论文(特指《channel polarization……》)的第VI-A节中对“对称的二元离散无记忆信道”的性质进行了详细的说明,参考文献【1】的第II节中对此也有描述。
对于一个无记忆信道W,我们假设它的输入为二进制数,且它是对称的,则有W:X→Y,其中X为输入符号集,X={0,1};Y为输出符号集,Y任意。根据定义,对于Y,存在一个恒等排列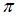 满足:
满足:
i) ![]() ;
;
ii) ![]() ,对于所有的y∈Y都成立。
,对于所有的y∈Y都成立。
为了方便起见,我们将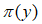 记为
记为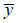 ,并称
,并称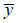 和y为共轭对。我们假设输出符号集Y为一个有限输出集(这个假设,在将算法推广到具有连续输出符号集的信道中时,会被证明)。
和y为共轭对。我们假设输出符号集Y为一个有限输出集(这个假设,在将算法推广到具有连续输出符号集的信道中时,会被证明)。
在Arikan论文的第VI-A节中,给出了这样一个定理:
Proposition 13(定理13):
如果一个B-DMC W是对称的,那么,
和
也是对称的,并且有:
其中运算 “·” 是一种速记。我们简记x·y:当x=0时,x·y → y;当x=1时,x·y→
。如同上面的定义,y和
为共轭对。
这是一个非常重要的结论,我们将在下面的信道操作中多次使用这个公式来进行计算的化简,请读者留意。
Arikan论文中给出了定理13的证明。
Part3.合并函数
从逻辑顺序角度考虑,我们先来探讨一下合并函数的内容。不过在这之前,我们必须先熟悉一下弱化信道与强化信道,这对于合并函数的介绍是必不可少的。
弱化信道
对于原始信道W:X→Y,对于信道Q:X→Z,若存在一个中间信道P:Y→Z,使得对于所有的x和z都有:
那么,我们写
,指代Q相对于W是弱化的。
强化信道
强化信道的描述与弱化信道类似,实际上,只需要将上式中的W和Q调换位置,就能够得到强化信道的表述:
写
,指代Q'相对于W是强化的。
对合并函数的理解从一个引理开始:
Lemma7:
设W:X→Y为BMS信道,假设y1,y2为输出字符集Y中的符号。对于信道Q:X→Z,定义其输出字符集Z为:
则,对于所有的x和z,定义:
那么,有
。
引理7中,字符集Z中的“\”表示“不包含”。
我们可以看到,在这个引理之中,我们放入了一个原始的W信道,得到了一个弱化信道Q。并且从W到Q,信道的输出字符集的大小发生了改变,Q字符集大小比W小2。因此,从这一点来看,我们可以通过引理 7同时得到一个弱化的、具有更小字符集的BMS信道。
引理7的证明并不难。我们只需要对中间信道P进行巧妙的定义:
对于中间信道P:Y→Z,从Y到Z的映射关系为: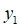 和
和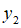 以100%的概率映射为
以100%的概率映射为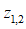 ,
,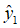 和
和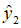 以100%的概率映射为
以100%的概率映射为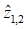 ,其余的符号一一映射为自身。
,其余的符号一一映射为自身。
显然,这样的中间信道是存在的,根据前面的描述,Q是W的弱化信道。
得证。
合并函数是用来解决因Arikan信道合并迭代公式造成的信道输出字符集爆炸增长的有力工具。根据引理7,对于一个具有v大小输出字符集的原始信道W,通过合并一对符号(及其共轭符号)的操作,我们每次都能使信道的输出字符集大小减2。通过多次调用这一操作,我们能够将W的输出字符集大小降到任意的大小μ。在【1】中,μ也用来表示“保真度”,一般来说,μ越大,合并函数的调用次数越少,系统性能越好,相应输出字符集也就越大,极化码构造算法的计算复杂度也就越高。
现在,我们有了合并函数这个有力的工具,但是要应用它,还有一个问题需要解决。在每一次的合并操作中,我们应该合并哪两个符号,是在输出符号集中随意挑选吗?还是需要遵循一定的原则?
【1】中的定理8对此进行了限定。
Theorem8
对于BMS信道W:X→Y,输出字符集Y有m个元素,假设有:
1 ≤ LR(y1) ≤ LR(y2) ≤ ······ ≤ LR(ym)
对于Y中任意两个符号a,b,设I(a,b)为合并后信道容量的大小。则,对于 1 ≤ i ≤ j ≤ k ≤ m,有:
定理8中,LR(y)表示似然判决下,y符号的最大似然值。通过定理8,我们可以发现,对相邻两个符号进行合并后所得到的信道的信道容量,总是大于非相邻符号的合并结果。这一定理指导我们在每一次合并时,都选择相邻符号进行合并。定理8的证明在【1】的附录中给出。
为此,我们对W信道的输出符号集Y按照最大似然值排序。假设输出符号集Y大小为2L,包含L个共轭对。
注意到定理8中的似然值排序,有隐含条件LR≥1。
似然值定义为:
根据对称信道的定义: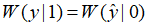 ,可以得到,对于
,可以得到,对于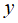 有:
有: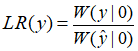
同样,对于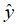 有:
有: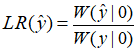 因此,对于共轭对
因此,对于共轭对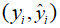 ,1 ≤ i ≤ L ,二者必定有一个满足似然值大于等于1。我们挑选出这个符号作为这对共轭对的代表,参与似然值的排序,最终得到:
,1 ≤ i ≤ L ,二者必定有一个满足似然值大于等于1。我们挑选出这个符号作为这对共轭对的代表,参与似然值的排序,最终得到: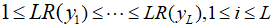
当我们将相邻两个符号 yi 和 yi+1 合并为 z 后,有: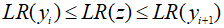
除此之外,为了在合并操作的过程中,尽可能少的损失信道容量,我们倾向于选择合并前后信道容量变化最小的那一对相邻元素。因此,在对输出符号集按照似然值排序之后,我们在合并之前还要做的一项工作就是,寻找信道亏损最小的相邻元素。我们设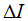 为合并前后信道的亏损,并以此为挑选合并相邻元素的依据。
为合并前后信道的亏损,并以此为挑选合并相邻元素的依据。
遵循【1】中的符号命名规则,我们设 a,b,a',b',分别表示: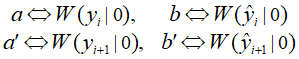 定义
定义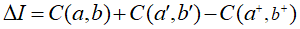
其中: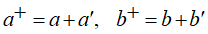
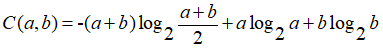
这样,合并之前,我们通过计算所有相邻元素合并后信道容量的亏损,找到亏损值最小的那一对相邻元素就可以了。
【1】第V节中对这部分内容的介绍十分详细,给出了包括合并函数中诸如堆栈、链表、指针的相关数据结构概念的介绍,并简述了合并函数的算法实现,思路非常清晰,可作为编程参考。
以上对合并函数的介绍,仅仅针对信道弱化操作展开。合并还可以通过信道强化操作,这部分内容稍微复杂一些,我无法表述清楚,请读者自行探索。
下一节中,我们将着重介绍信道弱化与信道强化操作,如果篇幅允许,我们将探索二元高斯信道下tal-vardy算法的应用。



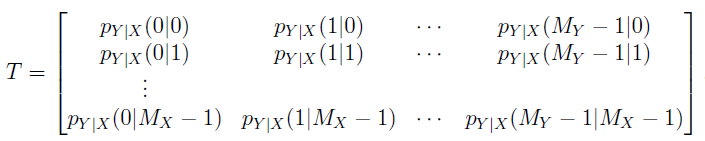
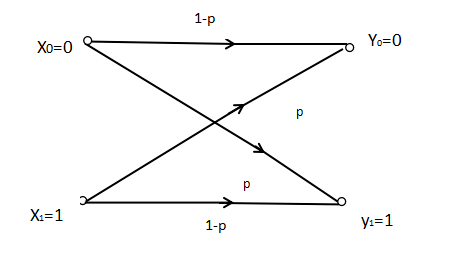 图2 二元对称信道
图2 二元对称信道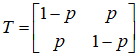

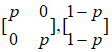
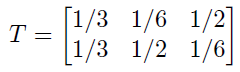
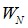 和
和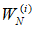 也是对称的,并且有:
也是对称的,并且有: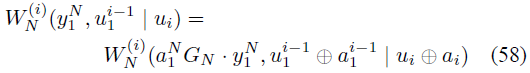 其中运算 “·” 是一种速记。我们简记x·y:当x=0时,x·y → y;当x=1时,x·y→
其中运算 “·” 是一种速记。我们简记x·y:当x=0时,x·y → y;当x=1时,x·y→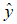 。如同上面的定义,y和
。如同上面的定义,y和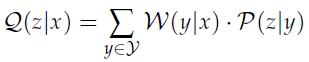 那么,我们写
那么,我们写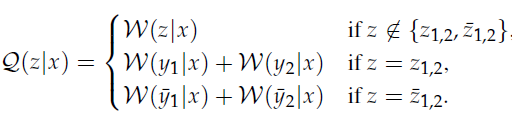
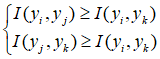

 浙公网安备 33010602011771号
浙公网安备 33010602011771号