luogu P3195 玩具装箱 斜率优化题解

【题意简述】

现有n个物品，第i个物品的长度为C_i。可以制造若干个容器，容器的数量和长度不限制，但是只能把连续若干个物品放入容器中。把物品区间[i,j]放入同一个容器中，长度为

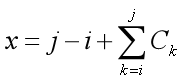
，每一个容器的制造代价为，L为给定常数。求最小代价之和。

【数据范围】对于100%的数据，。

【原题链接】

如果只要部分分，那么容易设计较慢的的算法。状态转移方程如下：

 

 

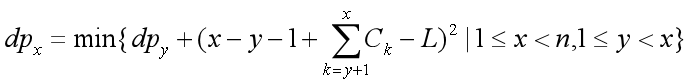
这是O(n³)的。还有很多优化空间。做前缀和，可以进一步优化到O(n²)。实测30pts。

 

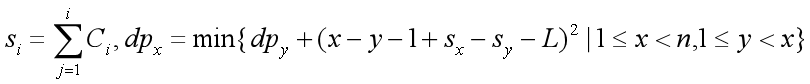
如果还要进一步优化，需要整理式子（为了叙述方便，x和y的范围略去不写）：

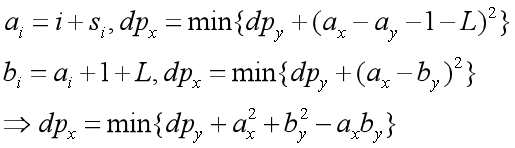
若j>k，且对于x说，从j比从k转移来的优，则有不等式：

 

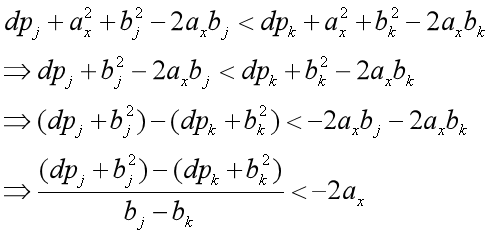
将b所表示的值代入分母，得：

 

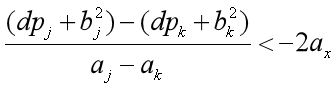
就得到斜率的式子了。以这样的规则在单调队列中弹队首、队尾即可。

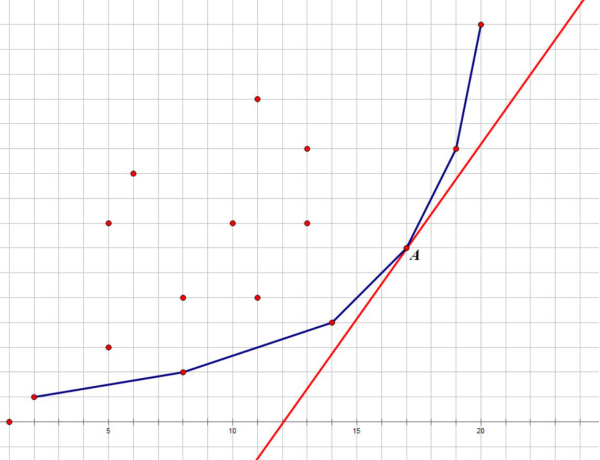
再借助图片理解：无论凸壳里面有多少个点，那条红色的直线都只会先碰到凸壳上的点，即只会在凸壳上的某一个点转移（如下图A点）。

 

 

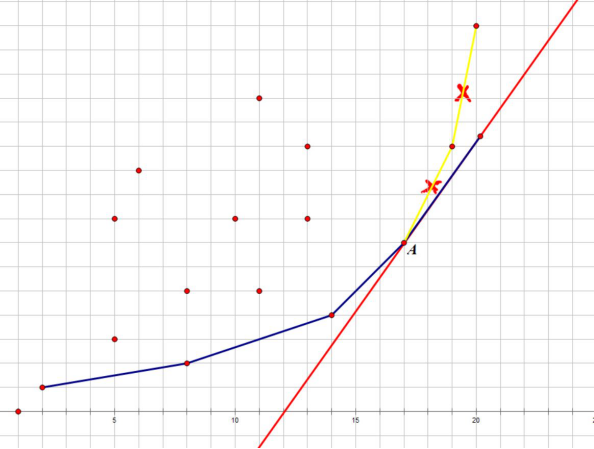
之后，两条黄色的、被叉掉的线段被包括在凸壳里面了，可以排除，被红色线代替了。

 

 之后就是代码了。

#include<cstdio>
#include<iostream>
#define int long long
using namespace std;
int dp[50010];
int n,L,c[50010],s[50010],a[50010];
int front=1,rear=1,q[50010];
inline double slope(int j,int k){
    int x1=a[j],y1=dp[j]+(a[j]+1+L)*(a[j]+1+L);
    int x2=a[k],y2=dp[k]+(a[k]+1+L)*(a[k]+1+L);
    return double(y1-y2)/double(x1-x2);
}
inline int f(int x,int y){
    return dp[y]+(a[x]-a[y]-1-L)*(a[x]-a[y]-1-L);
}
signed main(){
    ios::sync_with_stdio(false);
    cin>>n>>L;
    for(int i=1;i<=n;i++){
        cin>>c[i];
        s[i]=s[i-1]+c[i];
        a[i]=s[i]+i;
    }
    for(int i=1;i<=n;i++){
        while(front<rear&&slope(q[front],q[front+1])<=2*a[i])front++;
        dp[i]=f(i,q[front]);
        while(front<rear&&slope(q[rear],q[rear-1])>slope(i,q[rear]))rear--;
        q[++rear]=i;
    }
    cout<<dp[n]<<endl;
    return 0;
}

（完）