NOIP2008 传纸条 题解

题目链接：传纸条

0、说在前面

      不要被题目给局限了思维，其实小渊传给小轩再返回得到的答案和小渊通过两条不同的路径把两张纸条分别传到小轩手里是完全相同的，不需要考虑两张纸条传递的方向不同。（由于代码是分开两次写的，的含义不同，谅解一下）

 

1、四维空间存储状态dp

首先想到的肯定是用四维数组存储dp状态。用四维数组f[i][j][k][l]表示第1张纸条到达(i,j)的位置，第2张纸条到达(k,l)的位置时得到的最优值。考虑到两张纸条都可能从左边或上面传递过来。（第一张纸条可能来自(i,j-1)或(i-1,j)，第二张纸条可能来自(k,l-1)或(k-1,l)）容易得到状态转移方程：

f[i][j][k][l]=max{f[i-1][j][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k-1][l],f[i][j-1][k][l-1}

 

 

（m表示行数n表示列数）

方程推出来后就是代码了。

#include<iostream>

using namespace std;

int n,m,map[55][55],f[55][55][55][55];

inline int get_max(int num1,int num2,int num3,int num4)

{

   num1=max(num1,num2);

   num1=max(num1,num3);

   num1=max(num1,num4);

   return num1;

}

int main()

{

   cin>>m>>n;

   for(int i=1;i<=m;i++)

     for(int j=1;j<=n;j++)

        cin>>map[i][j];

   for(int i=1;i<=m;i++)

     for(int j=1;j<=n;j++)

        for(int k=1;k<=m;k++)

          for(int l=j+1;l<=n;l++)

             f[i][j][k][l]=map[i][j]+map[k][l]+get_max(f[i-1][j][k-1][l],f[i-1][j][k][l-1],f[i][j-1][k-1][l],f[i][j-1][k][l-1]);

   cout<<f[m][n-1][m-1][n]<<endl;

   return 0;

}

 

 

3、三维空间存储状态dp

      虽然用四维数组空间不会炸（n,m<=50），但是如果n、m再大一点就是稳稳地炸。我在题解区找到了一道题：大教室中传纸条（n,m<=200）。四维的dp就无能为力了，必须要减维压空间。有必要从另一个角度思考状态的设计。如下图所示：（这里用n表示行数m表示列数）

 

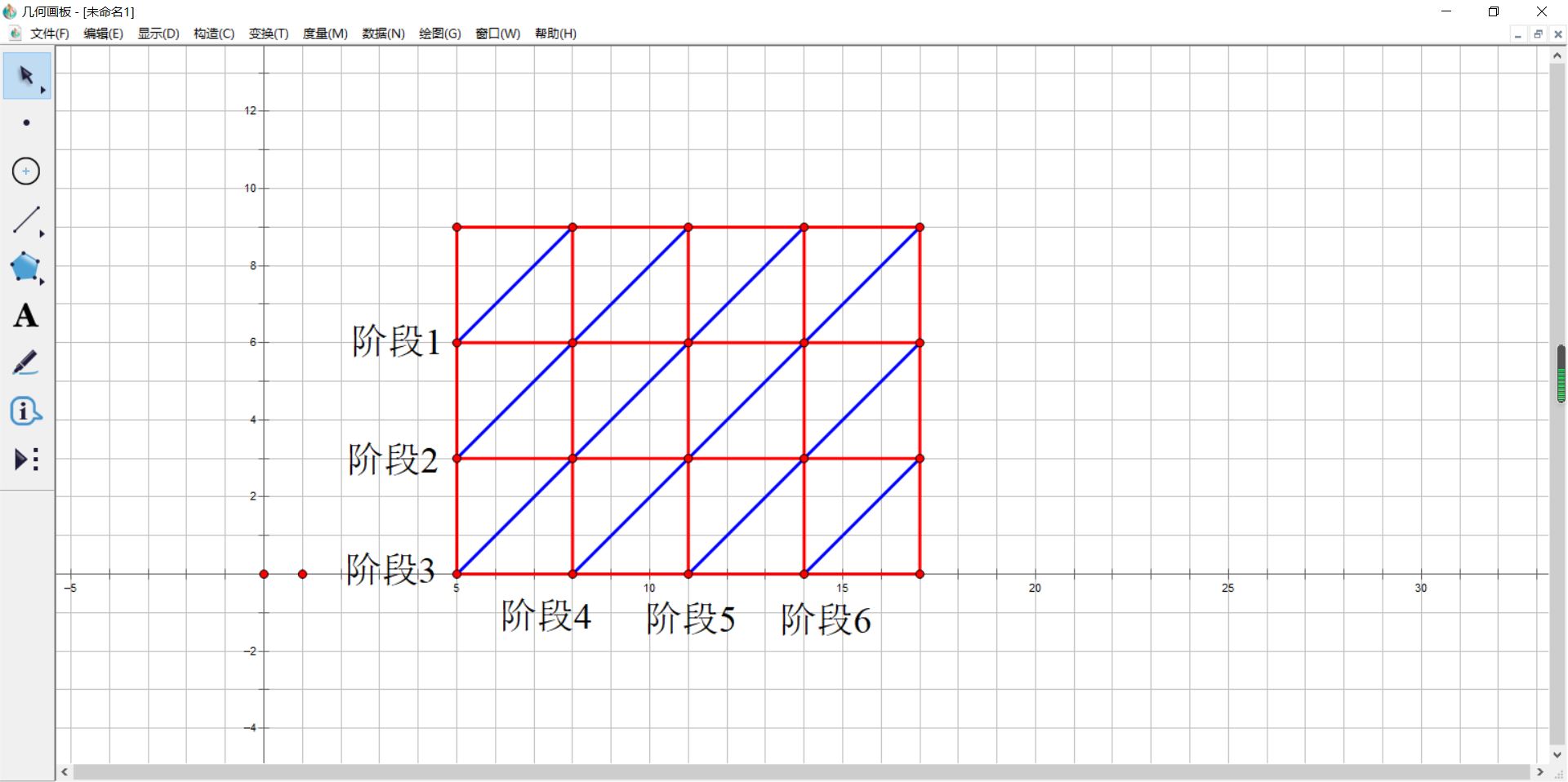
把每个方格看作一个同学，则对角线的条数为n+m-1，即有n+m-1个阶段。我们发现：（1）两张纸条同时走任意多步都会在同一对角线上；（2）只要确定了横坐标就可以确定纵坐标。若设stage表示第几个阶段，则对于任意的(x,y)，都有y=stage-x+1（当然是满足1<=x<=n,1<=y<=m的二元组(x,y)）。仍然考虑当前点可能来自左和上两个方向。可以发现规律：对于任意的二元组(stage,x)（不是坐标），他的上面是(stage-1,x)，左面是(stage-1,x-1)。由此推出状态转移方程：

 f[stage][x1][x2]=max{f[stage-1][x1][x2],f[stage-1][x1][x2-1],f[stage-1][x1-1][x2],f[stage-1][x1-1][x2-1]}+map[x1][stage-x1+1]+map[x2][stage-x2+1]

      剩下的就是代码了。（此代码在大教室中传纸条上只能得70分，后三个点炸了）

#include<cstring>

#include<iostream>

using namespace std;

int n,m,map[205][205],f[405][205][205];

int main()

{

   cin>>n>>m;

   for(int i=1;i<=n;i++)

     for(int j=1;j<=m;j++)

        cin>>map[i][j];

   for(int stage=1;stage<=n+m-1;stage++)

     for(int p1=1;p1<=stage;p1++)

        for(int p2=p1+1;p2<=stage;p2++)

          f[stage][p1][p2]=max(max(f[stage-1][p1-1][p2],f[stage-1][p1][p2-1]),max(f[stage-1][p1-1][p2-1],f[stage-1][p1][p2]))+map[p1][stage-p1+1]+map[p2][stage-p2+1];

   cout<<f[n+m-2][n-1][n]<<endl;

   return 0;

}

4、二维空间存储状态dp（三维压缩）

      二维的压缩并不需要换一个角度思考，直接对三维的进行压缩就OK了。

      我们发现，每一个stage只和stage-1阶段有关，这让我想起了背包的一维压缩算法。在这里，我们可以省略掉stage的一维，并把p1,p2倒序循环。为什么要倒序呢？因为p1,p2正序循环的话，就会破坏原来的状态，后面的就一直在用stage的阶段更新，而这是错误的。做法同三维，这里不再赘述。接下来便是代码。

#include<cstring>

#include<iostream>

using namespace std;

int n,m,map[205][205],f[205][205];

int main()

{

   cin>>n>>m;

   for(int i=1;i<=n;i++)

     for(int j=1;j<=m;j++)

        cin>>map[i][j];

   for(int stage=1;stage<=n+m-1;stage++)

     for(int p1=stage;p1>=1;p1--)

        for(int p2=stage;p2>=p1+1;p2--)

        {

          int q1=stage-p1+1;

          int q2=stage-p2+1;

          if(p1<1||p1>n||p2<1||p2>n)continue;

          if(q1<1||q1>m||q1<1||q2>m)continue;

          f[p1][p2]=max(max(f[p1-1][p2],f[p1][p2-1]),max(f[p1-1][p2-1],f[p1][p2]))+map[p1][stage-p1+1]+map[p2][stage-p2+1];

        }

   cout<<f[n-1][n]<<endl;

   return 0;

}

(完）