数学期望DP学习笔记

数学期望： 在概率论和统计学中，数学期望(mathematic expectation)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。——摘自百度百科
不懂？太正常了，百度百科就是不写人话。
举个栗子解释一下：在一次膜你赛中，小 z 预估自己有 $0.5$ 的概率考 $300$ 分，$0.3$ 的概率考250分，$0.2$ 的概率考 $200$分，计算方法与加权平均值有些类似，那她得分的数学期望即是： $0.5\times 300+0.3\times 250+0.2\times 200=265pts$。
具体地，记第 $i$ 种结果的概率为 $p_i$，结果得分为 $f_i$，那么 $x$ 的期望 $E(x)=\sum _{i=1}^x{p}_i\times f_i$。
注意，$\sum _{i=1}^x{p}_i=1$，即所有概率总和必须是 $1$。

---

Problem1 P4316 绿豆蛙的归宿
题意简述
给出一张 DAG，保证连通图，随机行走，求 $1$ 到 $n$ 的路径长度期望。具体地，若当前在点 $u$，出边数为 $o{d}_u$，则走到每一条出边的概率相等，都为 $\frac{1}{o{d}_u}$。
题目解析
我们设 $f_i$ 表示从 $1$ 到 $i$ 的路径长度期望，答案显然是 $f_n$。
但手算样例，我们看到如下情况，$f_1$ 显然为 $0$，$f_2$ 易得为 $0.5$，$f_3$ 如何计算？

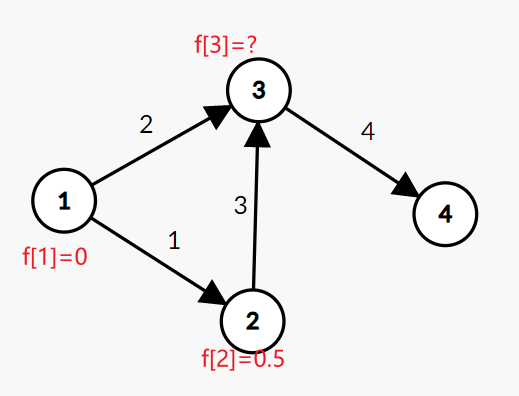
显然我们还需要考虑从 $1$ 到 $3$ 的概率。但我们感觉这种方法略微繁琐，正推不方便，不妨逆推，也就是设 $f_i$ 表示从 $i$ 到 $n$ 的路径长度期望，此时答案为 $f_1$，初始状态 $f_n=0$。
可以得出转移方程，当前在点 $u$，$f_u=\frac{1}{o{d}_u}\times \sum f_v+w_{u,v}$。
实现中，我们要逆推，所以两种方法处理图：记忆化搜索或者建反图拓扑排序。
代码实现
$1.$ 记忆化搜索

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e5+10;
int n,m;
int x,y;
double z;
struct edge{int v,next;double w;}e[N<<1];
int head[N],tot;
inline void add(int u,int v,double w){e[++tot].v=v,e[tot].w=w,e[tot].next=head[u],head[u]=tot;}
double chu[N];
double f[N];

void dfs(int u){
	if(f[u]) return ;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v;
		if(!f[v]) dfs(v);
		f[u]+=f[v]+e[i].w;
	}
	if(chu[u]) f[u]/=chu[u];
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i) scanf("%d%d%lf",&x,&y,&z),add(x,y,z),chu[x]++; 
	dfs(1);
	printf("%.2lf",f[1]);
	return 0;
}

$2.$ 反图拓扑

#include<queue>
#include<cstdio>
#include<iostream>
using namespace std;
const int N=1e5+100;
const int M=2*N;
int n,m;
struct node{
	int ver,nxt;
	double edge;
}e[M];
int head[N],tot;
int in[N],out[N];
double f[N],g[N];
void add(int x,int y,double z){
	e[++tot]={y,head[x],z};
	head[x]=tot;
}
queue<int> q;
void topsort(){
	f[1]=0.0;
	g[1]=1.0;
	q.push(1);
	while(q.size()){
		int x=q.front();
		q.pop();
		for(int i=head[x];i;i=e[i].nxt){
			int y=e[i].ver;
			double z=e[i].edge;
			f[y]+=(f[x]+g[x]*z)/out[x];
			g[y]+=g[x]/out[x];
			in[y]--;
			if(in[y]==0){
				q.push(y);
			}
		}
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int x,y;
		double z;
		scanf("%d%d%lf",&x,&y,&z);
		add(x,y,z);
		in[y]++;
		out[x]++;
	}
	topsort();
	printf("%.2lf\n",f[n]);
	return 0;
}

（法 $2$ 代码来自 此间的少年fu）。

---

Problem2 蓝桥杯 2022 省赛 A 组 E 题 （蓝桥杯终于出了个好题。）
题意简述
有一只虫想要爬上高度为 $n$ 的树，初始位于树根, 即高度为 $0$，当它从高度 $i-1$ 爬到高度 $i$ 时有 $p_i$ 的概率掉回树根, 求它从树根爬到树顶时，花费总时间的数学期望（一次尝试向上爬花费时间为 $1$）。
题目解析
类似的套路，我们设 $f_i$ 表示从 $i$ 爬到 $n$ 时间的数学期望，答案即为 $f_0$。
则从 $i$ 成功上到 $i+1$ 的概率是 $1-p_{i+1}$，掉回树根的概率 $p_{i+1}$，初始状态 $f_n=0$。
易得：$f_i=1+(1-p_{i+1})\times f_{i+1}+p_{i+1}\times f_0$。
发现此时的 $f_i$ 与 $f_{i+1}$ 和 $f_0$ 有关。有后效性的 DP？怎么办呢？
我们尝试多写几项寻找一下规律：
$f_0=1+(1-p_1)\times f_1+p_1\times f_0$
$f_1=1+(1-p_2)\times f_2+p_2\times f_0$
$f_2=1+(1-p_3)\times f_3+p_3\times f_0$
解方程组……高斯消元会 TLE……
于是直接代入可得 $f_0=1+(1-p_1)+(1-p_1)\times (1-p_2)+(1-p_1)\times (1-p_2)\times (1-p_3)\times f_n+[p_1+(1-p_1)\times p_2+(1-p_1)\times (1-p_2)\times p_3]\times f_0$