一个数组管理三个栈
一个数组管理三个栈
一个数组管理两个栈的思路是数组两端相向运动,这样能够动态调整;另一个思路是将数组均分为两部分,这样的缺点是不能动态调整。同样的,一个数组管理三个栈也有两个思路,一个是数组均分为三个部分,不能动态调整;另一个思路是两个栈数组两端相向运动,另一个栈根据其它两个栈的栈顶在二者中间某处布局(不一定是整个数组的正中间),这样三个栈能够相对的动态调整,如图所示:
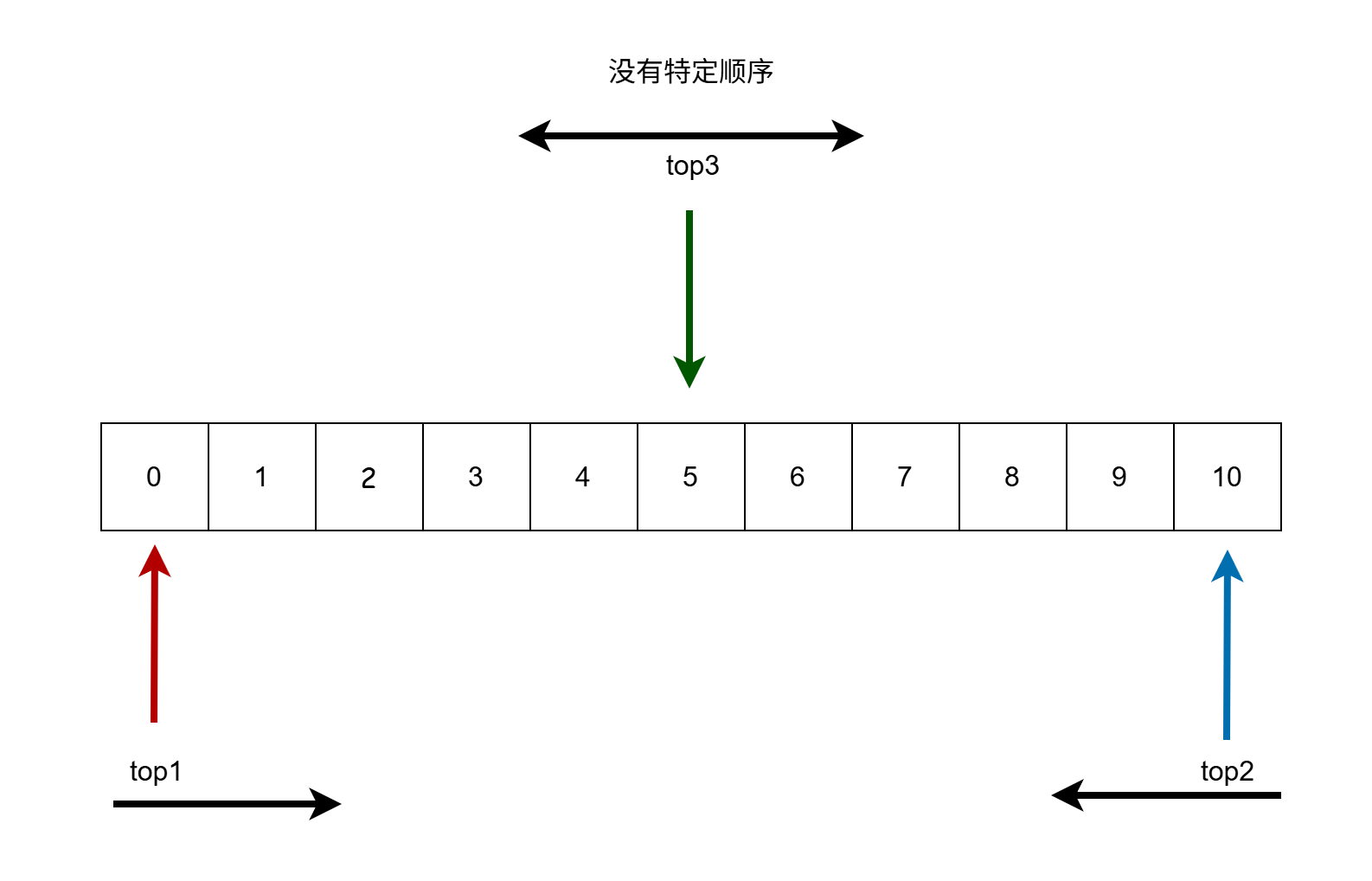
图中top1、top2、top3分别表示栈1、栈2、栈3的栈顶。第三个栈的扩充顺序是另外两个栈距离第三个栈的可用空间决定,哪边空间大则选择哪边。比如top2指向8,top1指向0,第三个栈已用空间为5,那么第三个栈新增的空间应该是4,因为5距离0可用空间为4个单位,而8距离5可用空间为2个单位。
所以这就引出了一个问题,不同于从两端开始的栈,其数据位置是非常容易跟踪的,要么递增要么递减。第三个栈的空间是跳动的,我们需要追踪它使用了哪些空间,否则压入与弹出操作就会异常,另一方面,我们需要计算其它两个栈距离第三个栈的可用空间,这个可用空间并非栈顶的差值,因为第三个栈的栈顶是跳动的,但是我们容易知道第三个栈的栈顶一定在上一次的左右边界中计算得出。所以对于第三个栈我们需要追加一个数据结构来跟踪它的信息路径,通常也采用一个栈,只不过这里要特殊化处理。数据部分的代码如下:
private:
static const int CAPCITY = 20;
Object arr[ CAPCITY ];
int top1, top2;
class Table
{
private:
int arr[ CAPCITY ];
int size;
int min_position, max_position;
int top;
public:
// 暂时略去
};
Table top3;
public:
// 暂时略去
也就是说top3作为中间的栈本身被封装为一个类,本来栈顶应该指向栈的最后数据,这里处理为追踪栈的信息。它记录了压入第三个栈时占用了数组的哪些空间,比如第三个栈先后占用了5,6,4的空间则arr[ CAPCITY ]先后记录了5,6,4。这样top3所指向的栈顶实际上就是top3.arr[ top ],通过这样封装可以避免数组中三个栈出现冲突。min_position与maxposition则记录了栈3的左右边界,在例子中min_position为4,而max_position为6。
栈的核心操作就是压入与弹出,而这两个操作都需要注意栈的可用空间。一个数组管理三个栈尤其需要注意可用空间的检查,因为数组是线性结构,三个栈在其上无论采用什么方法它们也是线性的,因此第三个栈需要检查与另外两个栈是否冲突以及另外两个栈与第三个栈是否冲突。
bool testClash( int other_position )
{
return other_position == min_position || other_position == max_position;
}
此外,我们要知道栈3的栈顶,因为栈3是被封装,所以额外的方法。
int topTable( ) const
{
if( !empty( ) )
return arr[ top ];
return -1;
}
注意到,这个返回的并不是栈3的栈顶元素,而是位置。
栈3每压入或弹出一个元素,其位置信息都要更新,所以对于top3而言也有压入与弹出,只不过是位置信息。
// first、second分别是栈1、栈2的栈顶位置信息
bool push( int first, int second )
{
if( !full( ) )
{
if( empty( ) && second - first > 1 )
{
arr[ ++top ] = ( first + second ) / 2;
min_position = max_position = arr[ top ];
}
else if( min_position - first > second - max_position )
arr[ ++top ] = --min_position;
else
arr[ ++top ] = ++max_position;
++size;
return true;
}
return false;
}
void pop( )
{
if( !empty( ) )
{
if( arr[ top ] == min_position )
++min_position;
else
--max_position;
--top;
}
}
实现逻辑正是前面所讨论的哪边可用空间大就将新的位置信息压入到哪边并做更新,可用空间的计算是栈3的边界与栈1、栈2的栈顶的差值,若相同默认插在朝向栈2的方向。一个特殊情况是栈3为空时,位置信息更新则需要根据栈1、栈2的栈顶差值计算得来,最好是在可用空间的中间位置。弹出操作要简单很多,因为栈顶位置一定是边界中的一个,更新边界后弹出一个位置信息即可。一个细节是push( )返回类型是bool,而pop( )的返回类型是void。原因在于压入元素操作要验证位置能否压入,所以需要返回值,但是弹出操作不需要验证。
主要的逻辑代码如上,完整代码如下:
// 栈3的位置信息
class Table
{
private:
int arr[ CAPCITY ];
int size;
int min_position, max_position;
int top;
public:
Table( ): size{ 0 }, top{ -1 }, min_position{ -1 }, max_position{ -1 } { }
bool empty( ) const { return !( top > -1 ); }
bool full( ) const { return !( size <= CAPCITY ); }
int topTable( ) const
{
if( !empty( ) )
return arr[ top ];
return -1;
}
bool push( int first, int second )
{
if( !full( ) )
{
if( empty( ) && second - first > 1 )
{
arr[ ++top ] = ( first + second ) / 2;
min_position = max_position = arr[ top ];
}
else if( min_position - first > second - max_position )
arr[ ++top ] = --min_position;
else
arr[ ++top ] = ++max_position;
++size;
return true;
}
return false;
}
void pop( )
{
if( !empty( ) )
{
if( arr[ top ] == min_position )
++min_position;
else
--max_position;
--top;
}
}
bool testClash( int other_position )
{ return other_position == min_position || other_position == max_position; }
};
栈1、栈2的操作改变较小,主要改变是压入元素时要验证是否有可用空间。
// 栈1的压入
void pushStack1( const Object & obj )
{
if( !top3.testClash( top1 + 1 ) && top1 + 1 < top2 )
arr[ ++top1 ] = obj;
else
std::cerr << "The first stack is full!\n";
}
// 栈2的压入
void pushStack2( const Object & obj )
{
if( !top3.testClash( top2 - 1 ) && top2 - 1 > top1 )
arr[ --top2 ] = obj;
else
std::cerr << "The second stack is full!\n";
}
其余方面并没有实际改变。上面讨论的栈3仅仅是位置信息,还没有实际压入或弹出元素,从逻辑上来看,与栈1、栈2也没有什么区别,只是多了一些检查。
void pushStack3( const Object & obj )
{
if( top3.push( top1, top2 ) )
arr[ top3.topTable( ) ] = obj;
else
std::cerr << "The third stack is full!\n";
}
void popStack3( )
{
if( !emptyStack3( ) )
{
top3.pop( );
top3 = top3.topTable( );
}
}
看上去栈3的弹出操作复杂了些,位置信息要弹出,而且栈顶的位置信息要更新。
下面给出完整的代码。
template <typename Object>
class ThreeStack
{
private:
static const int CAPCITY = 20;
Object arr[ CAPCITY ];
int top1, top2;
class Table
{
private:
int arr[ CAPCITY ];
int size;
int min_position, max_position;
int top;
public:
Table( ): size{ 0 }, top{ -1 }, min_position{ -1 }, max_position{ -1 } { }
bool empty( ) const { return !( top > -1 ); }
bool full( ) const { return !( size <= CAPCITY ); }
int topTable( ) const
{
if( !empty( ) )
return arr[ top ];
return -1;
}
bool push( int first, int second )
{
if( !full( ) )
{
if( empty( ) && second - first > 1 )
{
arr[ ++top ] = ( first + second ) / 2;
min_position = max_position = arr[ top ];
}
else if( min_position - first > second - max_position )
arr[ ++top ] = --min_position;
else
arr[ ++top ] = ++max_position;
++size;
return true;
}
return false;
}
void pop( )
{
if( !empty( ) )
{
if( arr[ top ] == min_position )
++min_position;
else
--max_position;
--top;
}
}
bool testClash( int other_position )
{ return other_position == min_position || other_position == max_position; }
};
Table top3;
public:
ThreeStack( ):top1{ -1 }, top2{ CAPCITY }, top3{ } { }
bool emptyStack1( ) const
{ return !( top1 > -1 ); }
const Object & topStack1( ) const
{
if( !emptyStack1( ) )
return arr[ top1 ];
std::cerr << "The first stack is empty!\n";
exit( EXIT_FAILURE );
}
void popStack1( )
{
if( !emptyStack1( ) )
--top1;
}
void pushStack1( const Object & obj )
{
if( !top3.testClash( top1 + 1 ) && top1 + 1 < top2 )
arr[ ++top1 ] = obj;
else
std::cerr << "The first stack is full!\n";
}
void pushStack1( Object && obj )
{
if( !top3.testClash( top1 + 1 ) && top1 + 1 < top2 )
arr[ ++top1 ] = std::move( obj );
else
std::cerr << "The first stack is full!\n";
}
bool emptyStack2( ) const
{ return !( top2 < CAPCITY ); }
const Object & topStack2( ) const
{
if( !emptyStack2( ) )
return arr[ top2 ];
std::cerr << "The second stack is empty!\n";
exit( EXIT_FAILURE );
}
void popStack2( )
{
if( !emptyStack2( ) )
++top2;
}
void pushStack2( const Object & obj )
{
if( !top3.testClash( top2 - 1 ) && top2 - 1 > top1 )
arr[ --top2 ] = obj;
else
std::cerr << "The second stack is full!\n";
}
void pushStack2( Object && obj )
{
if( !top3.testClash( top2 - 1 ) && top2 - 1 > top1 )
arr[ --top2 ] = std::move( obj );
else
std::cerr << "The second stack is full!\n";
}
bool emptyStack3( ) const
{ return top3.empty( ); }
const Object & topStack3( ) const
{
if( !emptyStack3( ) )
return arr[ top3.topTable( ) ];
std::cerr << "The third stack is empty!\n";
exit( EXIT_FAILURE );
}
void popStack3( )
{
if( !emptyStack3( ) )
{
top3.pop( );
top3 = top3.topTable( );
}
}
void pushStack3( const Object & obj )
{
if( top3.push( top1, top2 ) )
arr[ top3.topTable( ) ] = obj;
else
std::cerr << "The third stack is full!\n";
}
void pushStack3( Object && obj )
{
if( top3.push( top1, top2 ) )
arr[ top3.topTable( ) ] = std::move( obj );
else
std::cerr << "The third stack is full!\n";
}
};
读者可以根据需要扩展,这里我将基本函数简写,此外诸如top3.testClash( )用法看上去不直观,这可以重载运算符来实现。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号