耳分解 学习笔记

耳分解 学习笔记

耳分解

图 \(G\)，耳分解的定义是一系列子图 \(G_0, G_1, ..., G_k\)，其中子图两两不交且并为 \(G\)，其中 \(G_0\) 是一个环，\(G_{p}, p\ge 1\) 是简单路径 \(i\rightarrow j\)，其中除了 \(i, j\)，路径上其它点不在 \(\cup_{t = 0}^{p-1}G_t\) 中这被称为一个开耳，或环，除了环的一个端点，其它点都不在 \(\cup_{t = 0}^{p-1}G_t\) 中。

形象地，耳分解形如，除了白色，每一组颜色的边都是一个耳：

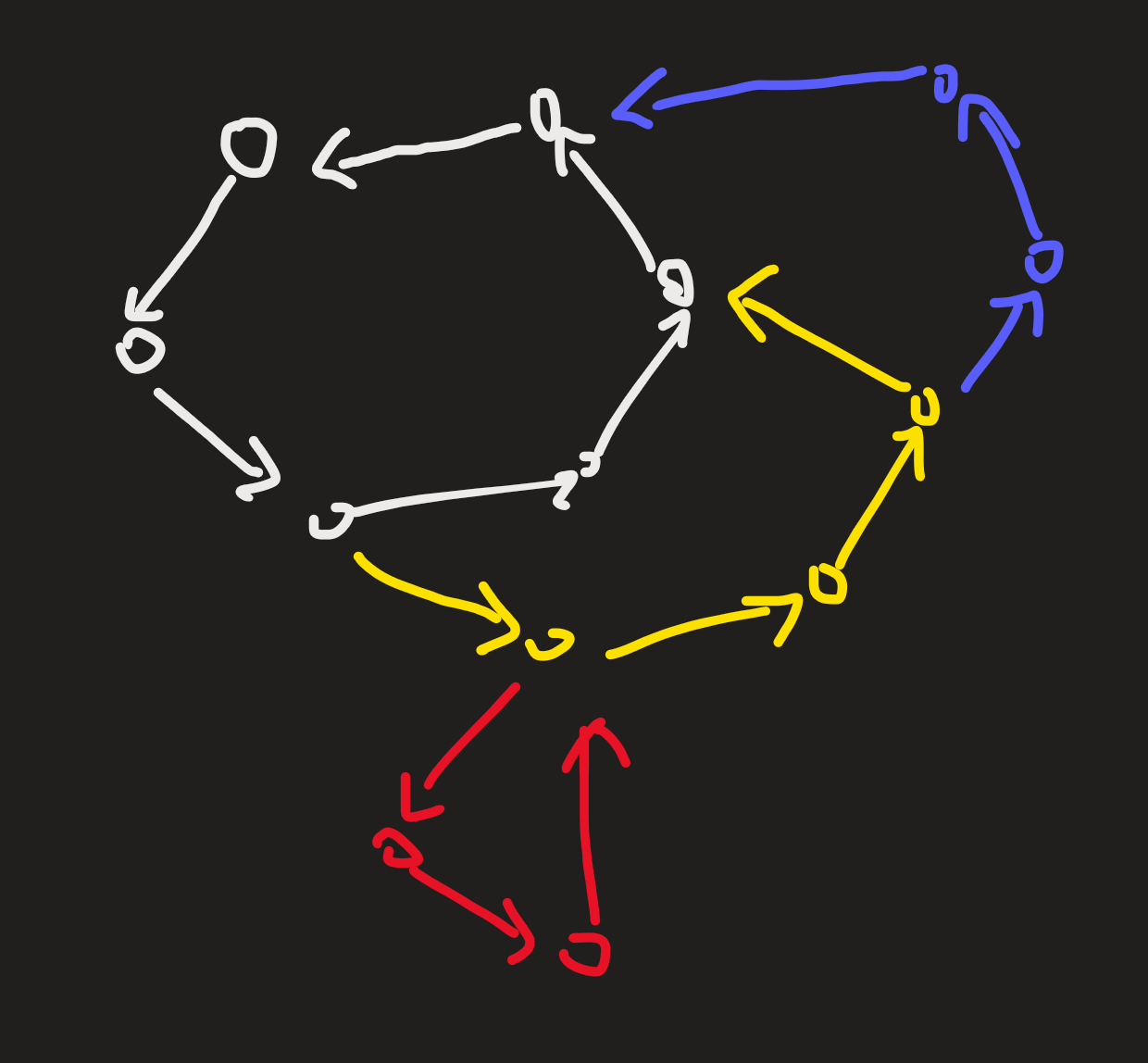
可以证明：

1. 一张有向图可以被耳分解当且仅当它强连通。
2. 一张无向图可以被耳分解当且仅当它边双连通。
3. 一张非 \(K_1, K_2\) 的点双连通无向图可以被耳分解。

[QOJ3301] Economic One-way Roads

给定一张无向图，每一条边两个方向各有一个代价，求定向为强连通图的最小代价。

\(n\le 18\)。
最小代价定向强连通，这类问题考虑耳分解。

转化

因为题目中所有边都要用上，所以首先我们做一个转化，如果我们已经得到了一个耳分解，那么这张图用耳分解的边一定是强连通图，剩下的边随便选也肯定还是强连通。

所以我们一开始默认所有的边都选择了代价较小的方向，而一个耳分解中选择一条边的代价就是 \(a_{i, j} - \min(a_{i, j}, a_{j, i})\)，也就是说如果这条边是代价较小的方向，那么没有代价，否则需要一些额外代价来改变它的方向。

这样问题就被转化为了求代价最小的耳分解。

\(O(3^n n^2)\)

考虑一个暴力的耳分解，令 \(f_{s}\) 表示包含 \(s\) 内点的最小耳分解，这个耳分解需要是闭合的，\(g_{s, i, j}\) 表示 \(i\) 到 \(j\) 的路径经过了 \(s\) 内的点的最小代价。

转移的时候枚举 \(t, s\cap t = 0\) 已经耳路径的端点 \(i, j\)，将 \(g_{t, i, j}\) 这条路径作为耳加入 \(s\)。

这样瓶颈在转移，复杂度是 \(O(3^nn^2)\)，无法通过。

\(O(2^nn^3)\)

上一个 DP 状态设计得太粗糙，进一步分割状态集合，我们可以得到新的状态描述： \(f_{s}\) 表示包含 \(s\) 内点的最小耳分解，这个耳分解需要是闭合的，\(g_{s, i, j}\) 表示包含 \(s\) 内点的耳分解，且当前耳分解不是闭合的，当前耳分解路径端点是 \(i, j\)。

考虑 \(g\) 的转移，枚举 \(i\) 下一步到达的节点 \(k\)，如果 \(k = j\)，那么当前耳分解闭合了，转移到 \(f_s\)，否则转移到 \(g_{s+k, k, j}\)，这里的 \(s+k\) 代表将 \(k\) 加入 \(s\) 集合得到的新集合。

如果耳分解闭合了，可能还需要拓展新的耳，枚举新的耳的端点 \(i, j\)，从 \(f_s\) 转移到 \(g_{s, i,j }\)。

注意这里如果 \(i =j\)，那么加入的不是一条开耳而是一个环，但是这种情况有一个问题，如果不加以约束，假设 \(i\) 下一个端点是 \(k\)，那么 \(g_{?,k,j}\) 有可能直接转移到 \(f\)，这样会出现一个重边。

为了避免这种情况，枚举 \(i\) 下两步到达的节点 \(k, p\)，要求 \(p \ne i\)。

设置初始值时不能设置开耳，只能设置一个环，为了避免重边同上处理。

不过在 \(i\ne j\) 的时候也可能会出现重边，也就是 \(i\rightarrow j, j\rightarrow i\)，但是这种情况下的重边是无意义的，因为这种重边没有扩展 \(s\) 集合还徒增了一些代价，该决策肯定不会被采纳。

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <ctime>
// #define int long long
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
typedef long long ll;
const int N = 18, INF = 1e9;
int n, a[N][N], g[1 << 18][N][N], f[1 << 18], c[N][N];
void cmin(int &a, int b) {
    if(a > b) a = b;
}
signed main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    clock_t stt = clock();
    cin >> n;
    for(int i = 0; i < n; i ++) for(int j = 0; j < n; j ++) cin >> a[i][j];
    for(int i = 0; i < n; i ++) for(int j = 0; j < n; j ++) c[i][j] = a[i][j] - min(a[i][j], a[j][i]), c[j][i] = a[j][i] - min(a[i][j], a[j][i]);
    memset(f, 0x3f, sizeof f), memset(g, 0x3f, sizeof g);
    for(int i = 0; i < n; i ++) {
        for(int k = 0; k < n; k ++) if(a[i][k] != -1)
            for(int p = 0; p < n; p ++) if(i != p && a[k][p] != -1 && k != p)
                cmin(g[(1 << k) | (1 << p) | (1 << i)][p][i], c[i][k] + c[k][p]);
    }
    int base = (1 << n) - 1;
    for(int s = 0; s < (1 << n); s ++) {
        for(int I = s, i, j; I; I &= I - 1)
            for(int J = s; J; J &= J - 1) {
                i = __builtin_ctz(I), j = __builtin_ctz(J);
                if(a[i][j] != -1) f[s] = min(f[s], g[s][i][j] + c[i][j]);
            } 
        for(int I = s, i, j; I; I &= I - 1)
            for(int J = s; J; J &= J - 1) {
                i = __builtin_ctz(I), j = __builtin_ctz(J);
                if(f[s] >= INF) continue;
                if(i == j) {
                    for(int K = base ^ s, k, p; K; K &= K - 1) {
                        k = __builtin_ctz(K);
                        if(a[i][k] == -1) continue;
                        for(int P = base ^ s; P; P &= P - 1) {
                            p = __builtin_ctz(P);
                            if(a[k][p] == -1 || k == p) continue;
                            cmin(g[s | (1 << k) | (1 << p)][p][j], f[s] + c[i][k] + c[k][p]);
                        }
                    }
                }
                else cmin(g[s][i][j], f[s]);
            }
        for(int I = s, i, j; I; I &= I - 1) {
            for(int J = s; J; J &= J - 1) {
                i = __builtin_ctz(I), j = __builtin_ctz(J);
                if(g[s][i][j] >= INF) continue;
                for(int K = base ^ s, k, p; K; K &= K - 1) {
                    k = __builtin_ctz(K);
                    if(a[i][k] != -1) cmin(g[s | (1 << k)][k][j], g[s][i][j] + c[i][k]);
                }
            }
        }
    }
    int ans = f[(1 << n) - 1];
    for(int i = 0; i < n; i ++) for(int j = 0; j < i; j ++) if(a[i][j] != -1) ans += min(a[i][j], a[j][i]);
    if(ans > 1000000000) cout << -1 << '\n';
    else cout << ans << '\n';
    cerr << (1.0 * clock() - stt) / CLOCKS_PER_SEC << "s\n";

    return 0;
}